基于雷管实际延时范围的逐孔爆破振动合成计算与应用
2019-02-27吴昊骏
吴昊骏,龚 敏
(北京科技大学土木与资源工程学院,北京 100083)
近年来对城市隧道爆破振动控制趋于高安全指标,需要精确设置爆破参数。由于隧道常用多孔微差爆破,药量、微差间隔时间与合成振速存在复杂的耦合关系,研究多段微差合成振速计算方法,对城市隧道爆破设计具有非常重要的意义。
自1985年Anderson[1]提出用单孔爆破振动数据计算微差合成振速以来,这一原理被广泛应用。Blair和Hinzen发展了线性[2]、非线性叠加方法[3];吴从师等[4]以台阶单孔爆破振动曲线为源函数,计算两孔时差0和25 ms的合成振动曲线,证实同段延时误差影响合成振速和单孔爆破振动波形具有重复性。徐全军等[5]用单孔样本函数对某爆破工程振动峰值预报,发现若在混凝土试验中精确控制两孔微差时间,则计算与实测波形吻合较好;陈士海等[6]研究两孔微差爆破不同时间的合成振动波形变化规律,指出微差时间为爆破主振1/2周期时振动降幅最大;其他学者[7-12]也进行了相关研究工作。
目前的困难是隧道实际微差爆破振动计算难以实现,以雷管段号时间计算合成振速误差很大。由于雷管各段均有延时范围,在此范围内将随机产生多种振动叠加,随着微差孔数不断增加形成海量的合成振动曲线。若从爆破精准控制与安全考虑,应分析全部振动组合,再按安全振速下最大振动曲线设置参数。但这涉及巨大的计算量且过程复杂,在过去不可能完成。为简化计算龚敏等提出在最初两孔起爆延时范围内计算所有可能振动曲线,选其中最大振速曲线再与第3起爆孔的延时时段内各时刻进行振动合成,以此类推最终曲线可视为多孔微差最大合成振动曲线[13]。然而最大振动曲线是否是由前段峰值曲线与后段延时范围内逐次叠加形成,仍有待进一步研究。
计算技术的发展给解决上述问题提供了可能,本文中以重庆渝中隧道工程为背景,根据各段雷管实际延时范围设计计算程序并优化算法,成功解算出8孔微差爆破百万种以上全部合成振动组合,分析了各段延时误差对振速影响;在研究第二临空面形成时间后提出城市隧道爆破药量计算新方法。
1 方 法
1.1 各段雷管段别延时范围的确定与振动合成曲线数量关系
如上所述,以名义段号时间进行微差振动合成计算不能满足城市精准控制爆破需要,本文先解决各段雷管起爆延时时间的测定问题,龚敏等[14]研究发现雷管样本的延时数据可代表批次雷管基本特性,据此以重庆渝中隧道工程为例,对各段雷管样本进行延时起时间测试。
首先确定各段雷管延期时间Δti的取值范围。在同一批次雷管中,每段随机抽取数个样本实测起爆时间,在各段实测结果中筛选出最早起爆时间Ti,earl及最迟起爆时间Ti,lat。得到第i段雷管起爆时间Δti范围:
Δti∈(Ti,earl,Ti,lat)i=1,2,3,…
(1)
式中:Δti为第i段雷管起爆时间;Ti,earl为第i段雷管起爆时间最小(早)值;Ti,lat为第i段雷管起爆时间最大(迟)值。
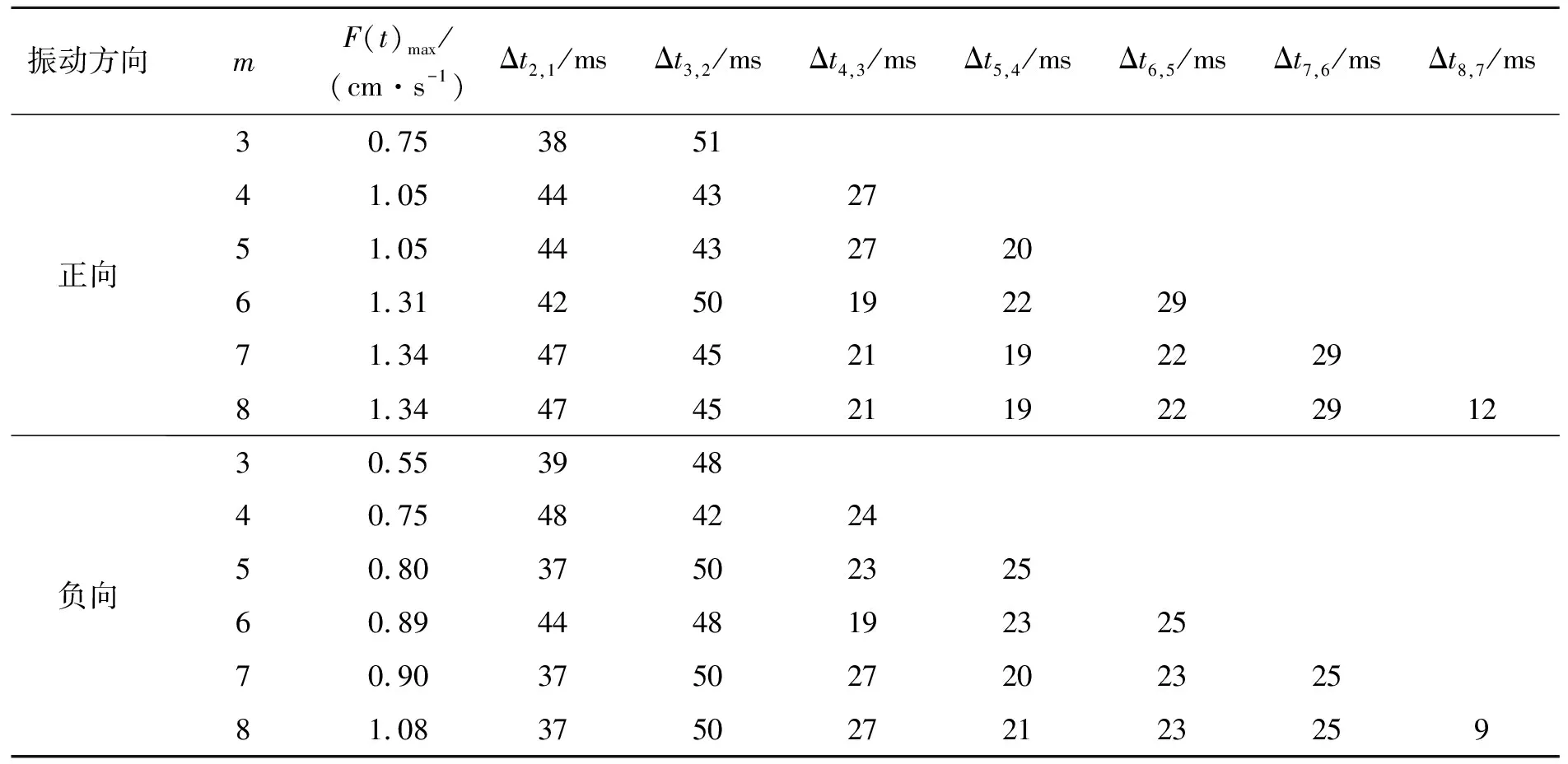
数据组中若存在Ti,earll 由实测雷管起爆时间得到段间微差时间Δti,i-1的范围: Δti,i-1∈(Ti,earl-Ti-1,lat,Ti,lat-Ti-1,earl)i=2,3,4,… (2) 图1 渝中隧道工程各段雷管起爆时间实测图Fig.1 Initiation times of detonators tested in Yuzhong tunnel project 重庆渝中隧道采用基于第二系列高精度非电雷管开发的定制25段非电雷管,每段取10个样本测试并记录数据,现设计采用8孔逐孔掏槽爆破,找出各段雷管最早起爆时间Ti,earl和最迟起爆时间Ti,lat。筛除易串段雷管段别后重新编号,这种个别跳段尽可能避免了段数减少,新的1~8段雷管起爆时间范围如图1所示,其中实测1段雷管无延时误差。 若在这8段雷管各实测延时范围内进行8孔逐孔掏槽,可能的微差爆破组合有114万余种(微差间隔以1 ms计)可能性,即存在114万种以上不同的合成振动曲线,以往由于工作量巨大及计算机软硬件发展限制,全部振动曲线难以计算获取和比较,必须采用新的方法加以解决。 在主要测点采集的单孔爆破波形,包含周围地质条件、爆区环境信息。受介质阻尼等因素的影响,波速最终会衰减为0。从初至波到幅值Amax/e(Amax为最大振幅,e为自然对数的底)处为波形主振段,持续时间为tmain。 叠加前对单孔波形进行时长截取,将截断时间t0之后的振速归零。该值太大,程序运行时间过长,获取结果缓慢;该值太小,最大叠加振速出现时,前期起爆的单孔波形振速可能已归零,计算不准确。因此保证最后一段波主振段结束时,首段波速刚好归零即可,即: t0=Tm,lat+tmain (3) 式中:t0为单孔波形截断时间;m为参与叠加的雷管总段数;Tm,lat为第m段(最后一段)雷管实测最迟起爆时间;tmain为单孔波形主振段持续时间。 编写MATLAB程序,将所截波形拟合成傅里叶级数形式,便于程序分析处理: (4) 式中:g(t)为单孔波形拟合函数;t为时间;n为级数;ω为基频;a0、aj、bj为拟合系数。 确定波形函数,实际上就是确定式(4)中基频值和各系数值: 式中:N为采样点个数;k为分点;tk为采样点横坐标;g(tk)为采样点纵坐标。 将式(4)扩展到时间全域,使各列波在任意叠加时刻均有意义: (5) 式中:f(t)为扩展的单孔波形函数;t为时间;t0为截断时间。 在不考虑第二临空面作用的前提下,按线性叠加理论对该药量单孔波形进行叠加,预测多孔合成波形及最大振速。对垂直振速分量进行叠加时,波形同向,可进行代数叠加: (6) 式中:F(t,Δti)为按起爆时间组Δti叠加得到的波形函数;m为参与叠加的雷管总段数; Δti为第i段雷管起爆时间。 至此,通过公式(6)再利用MATLAB软件多级For循环语言计算编程,可获得在各段延时时段内、多孔微差爆破所有可能合成振动组合的曲线。 如上所述,按照式(6)循环嵌套各段雷管Δti取不同值,获取所有波叠加后可能得到的时间-振速曲线F(t,Δti)后,找出该Δti组合下,各波形曲线F(t,Δti)的最大峰值F(t,Δti)max。 在众多F(t,Δti)max中,找出最大值F(t)max及对应Δti组合,为叠加最不利情况对应的最大振速: F(t)max={F(t,Δti)max}max (7) 在众多F(t,Δti)max中,找出最小值F(t)min及对应Δti组合,为叠加最有利情况对应的最大振速(微差降振效果最好的情况): F(t)min={F(t,Δti)max}min (8) 需要注意的是:为了找出最大合成振动曲线对应的合成峰值F(t)max及各段起爆时间Δti,程序在计算过程中需要保存大量的数据,普通计算机或服务器硬件配置无法满足如此庞大的数据存储需求。对此本文通过优化算法压缩数据存储量,成功完成了程序计算。 利用求得的各段起爆时间Δti,可求得各段微差时间Δti,i-1,其值应在式(2)确定的区间内: Δti,i-1=Δti-Δti-1(i=2,3,4,…) (9) 将以上步骤表示为流程,如图2所示。 图2 合成计算流程Fig.2 Superposition calculation process 以渝中隧道工程为例,搭载Xeon W3680 CPU、24 G内存64位计算机作为研究平台,将参与叠加的波列数与对应计算机运行时间列于表1中。由表1看出随着参与叠加波数的增加,计算机程序运行时间也不断增加。 表1 计算机运行时间统计Table 1 Statistical results of computer running times 据此结合计算机能力,通过波数较少的波形叠加耗时估计波数较多时程序运行的时间。方便合理调整微差时间的迭代间隔及波形的采样间距。 以上计算实例表明,在计算机正常配置下,考虑雷管各段延时范围的8孔微差爆破全部合成振动曲线计算时间为4.2 h,故对所有可能的微差合成爆破振动曲线分析处理可行,可作为今后爆破设计的参考。 计算8孔微差爆破振动最大值及相应的振动曲线只是精准设计重要的一环,这一方法只考虑了多段微差间隔对合成振速影响,没有涉及第二临空面形成对振速影响,将二者结合才能实现掏槽药量精准设计。 (1)第二临空面形成时间的确定 在笔者过去研究[13]基础上,现场实测逐孔逐段掏槽爆破振动曲线1,根据EMD法[15]结合爆前实测获取各段雷管准确起爆时刻;以此8个确定时刻及单孔单自由面爆破振动测试计算8孔微差爆破合成振动曲线2,由于曲线2没有考虑第二临空面对振速影响,将曲线1、2进行同时刻振速差异对比即知第二临空面形成时间,也即知第二临空面形成前的雷管段数m0。 (2)爆破应用 上述计算完成后,再根据需要以相同药量改变起爆间隔、不同药量起爆间隔固定两种方式进行设计应用:(a) 若只进行一次单孔爆破实验,对m0以前各段按逐孔爆破重复1.3计算过程,所有振动曲线的最大峰值如都不超安全振速则以其中最大药量为设计药量;若有任一振速超标则改变微差间隔(跳段)再进行计算直到获取安全药量; (b) 进行不同药量(一般2~3次)隧道单孔爆破振动测试,对m0以前各段按逐孔爆破重复1.3计算过程,选取所有振动曲线峰值不超标的最大药量作为设计药量,即实现控制振速下循环进尺最大化。 按傅里叶级数对测点采样数据进行拟合,得到单孔波形及掏槽孔分布情况如图3。其中正向最大振速为0.571 cm/s (3.9 ms),负向最大振速为-0.403 cm/s (17.6 ms),均未超过现场1.0 cm/s的安全振速要求。 图3 掏槽区布孔及单孔爆破振动波形Fig.3 Arrangement of cut-holes and single-hole vibration wave 参考波形衰减程度及计算机的运行能力,根据式(3)确定单孔波形主振段74 ms,结合第8段雷管最迟起爆时间195 ms,取前270 ms的采样数据进行分段拟合如式(10),编程计算傅里叶系数: (10) 式中:ω1、ω2为基频;a01、aj1、bj1、a02、aj2、bj2为拟合系数;t1为分段时间,取130 ms;t0为截断时间,取270 ms。 第一段,样本均值6.21×10-4,函数样本均值3×10-4,样本方差0.026,函数样本方差0.026;第二段,样本均值-2.81×10-5,函数样本均值-2.04×10-5,样本方差1.44×10-4,函数样本方差1.44×10-4。拟合效果较好。 以现场雷管样本实验得到的各段起爆时间Δti的范围为基础,暂不考虑第二临空面的消振效果,将第2列波、第3列波……第8列波,按照各起爆时间范围内的Δt2、Δt3……Δt8循环嵌套叠加,得到微差各段延时范围内所有可能的合成振动曲线,表2为程序计算的8孔微差爆破后形成的最大合成振速F(t)max及其对应的Δti,i-1组合。 表2 最大合成振动速度及对应微差时间组Table 2 Maximum superposed vibration velocity and corresponding millisecond times 按8列波叠加正向最不利情况计算得出的Δti,或按进一步求出的Δti,i-1=47,45,21,19,22,29,12 ms对各单孔波形进行叠加后,得到图4所示8孔微差起爆可能形成的最大合成振速曲线,各段微差起爆时刻为最不利起爆时差组合,这一计算结果为结合第二临空面形成进行爆破设计奠定了基础。 图4 8波叠加正向最不利情况时预测波形Fig.4 Worst predict waveform superposed by eight waves 图5 各幅值分量与单孔波形对应关系Fig.5 Corresponding relations between velocity components and single waveforms 波振动至187 ms(G峰)时,正向最大振速为1.340 cm/s,超过1.0 cm/s的安全振速要求,为单孔爆破最大振速的2.35倍,其余微差时间组合得到的最大振速都小于该结果,该组合为叠加最不利情况;负向最大振速为-0.605 cm/s,虽未超过安全振速要求,但也达到单孔实验负向最大振速的1.50倍。为进行比较,也按式(8)计算了降振最大的振动曲线,其峰值振速不大于单孔爆破最大振速。 所有振动曲线计算结果表明:同段延时范围即使在较小范围内,其合成振速之间的差异也可达57%(1-(0.571 cm/s)/(1.34 cm/s)),这是非常有意义的研究结果,它说明按现在施工中常采用的以标称段号设计爆破网络,难以做到精确控制爆破振速。 起爆187 ms时G峰出现,第8列波尚未出现,前7列波按照起爆时差参与振动。各列波贡献的幅值分量,表现在单孔波形(图3)上,分别等于g(187)、g(140)、g(95)、g(74)、g(55)、g(33)、g(4)。由于持续振动了较长时间,前3列的幅值分量g(187)、g(140)、g(95)均小于0.01 cm/s,而第4~7列波振动时间不长,幅值分量g(74)、g(55)、g(33)、g(4)相对较大(图5),做出了主要贡献。单个波幅值分量虽然不大,但因为个数较多,且全部处于波峰处,导致合成振速也很大。 综上,波形叠加作用早期,参与波数较少,合成振速取决于单个波形的较大波峰,后期参与叠加的振动波数量多,合成振速转而取决于处于波峰的子波个数。个数较多时,小振速也可导致叠加中后期最大合成振速出现。如果没有第二临空面的减振效果,则只能采取分离波形的方法避免波的叠加。 以上计算得到8孔微差爆破振动最大值及相应的振动曲线,今后只需获知雷管延时范围和进行简单的单孔爆破振动测试,即可解决类似多孔微差合成振动计算问题。然而要实现精准爆破设计,还需考虑第二临空面形成对振速的影响。目前关于第二临空面形成时间大多为经验认识,一般认为在50~120 ms之间,随现场地质条件和爆破参数不同而改变。本文用1.5节方法(1)确定第二临空面形成时间后,再与计算合成振速曲线结合进行爆破设计。 通过EMD法结合爆前样本实测数据,识别实测爆破振动曲线各段起爆时间后,按求得的Δti对8列单孔波形进行叠加计算(无延时误差范围),得到计算合成振动曲线,将计算合成波形与实测振动曲线进行对比,如图6所示。 图6 实测与合成爆破振动波形对比Fig.6 Comparison between the measured and superposed blasting vibration waveforms 从图6可看出在虚线框内时段实测与计算合成曲线波形相似、走向一致,主要峰谷出现时刻与幅值差别较小;60 ms后,实测波形平稳衰减,合成波形显示出叠加的效果,二者差异明显。第4段起爆后正向实测峰值0.25 cm/s,为正向合成峰值0.79 cm/s的31.6%。第6段起爆后,正向实测峰值0.20 cm/s仅为正向合成峰值0.45 cm/s的44.4%。据此可以确定现场第二临空面形成时间不超过60 ms。渝中隧道现场大量爆破振动测试数据均证实了这一结论的准确性。 通过以上分析可知,渝中隧道爆破第二临空面形成时间为60 ms。从图1可知,2段起爆延时范围37~49 ms,3段起爆时段87~92 ms,故在第3段起爆前第二临空面已经形成。因此只需进行1~2段延时时段内所有可能的微差爆破振动合成计算,以验证振速是否超标即可。 重复本文1.3节过程,尝试Δt2,1所有可能取值后发现:Δt2,1=48 ms时正向最大合成振速0.622 2 cm/s,满足安全振速控制要求(如图7所示)。1.0 kg判断为安全药量。由于现场条件与时间限制,现场只进行0.8 kg、1.0 kg单孔爆破实验,没有继续尝试1.2 kg单孔药量实验。在条件允许的情况下,应对不同药量分别进行单孔实验及爆破振动合成分析,选出同时满足安全振速和循环进尺最大的设计药量。 图7 第二临空面形成前波形合成Fig.7 Waveforms superposition before appearance of the second free surface 需指出的是,渝中隧道爆破时第二临空面出现时间在3段雷管起爆前,但其他地点因地质条件和布孔参数变化而不同,如在更高段别m0段前形成,则应计算前m0-1段微差爆破所有可能的合成振动曲线,再选择不同药量设计安全药量,也可在超标区间定向跳段改变起爆间隔以控制振速;在第二临空面形成后则改为两孔(多孔)同段起爆。 渝中隧道控制振速1.0 cm/s,左洞大断面面积149 m2,设计用CD法爆破开挖。根据4.2节研究成果,在首爆1区掏槽孔药量设计为1.0 kg,虽然第3段起爆范围(87~92 ms)为第二临空面形成以后,但考虑二者时间相近,为保险起见3段仍采用单孔单段掏槽,依据楔形掏槽孔位第4段相应为单孔单段;从第5段开始改为两孔一段爆破,图8为现场实际布孔图。2015年12月在渝中隧道ZK14+165.5-ZK14+195段进行了16次爆破,所有爆破均进行了振动测试,其中最大振速0.90 cm/s,平均振速0.65 cm/s,与3.2节计算吻合较好。 图8 设计CD法爆破开挖Fig.8 Blasting excavation design of CD method 如引言所述过去因条件所限,基于雷管各段延时误差的逐孔微差爆破振动合成少有研究,龚敏等曾采用简化算法[13]对8孔微差爆破进行了计算:在1~2段延时范围内以1 ms为增量计算所有合成振动曲线,仅取最大峰值振动所在曲线(一条)与3段延时范围内各时刻分别进行振动合成,以此类推得到8段起爆后的曲线被认定为最大合成振动曲线。然而这样有限次计算方法是否可靠仍无法验证。鉴于本文方法完整求出8孔微差爆破合成振动所有可能的振动曲线,自然也可准确获得最大振速的振动曲线,下面将分析前述方法的准确性,为方便比较将过去方法称为有限次叠加法,本文方法称为完全叠加法。 取相同单孔爆破振动波形前270 ms采样数据,进行有限次叠加法求最大振速,按正向叠加最不利情况,Δti,i-1=48,43,20,22,29,19,11 ms,按负向叠加最不利情况,Δti,i-1=48,40,25,23,25,17,17 ms。 图9 两种方法结果对比Fig.9 Compare the results of two methods 将两种方法所得最大合成振速进行对比,对比结果如图9所示,最左端为第3列波叠加振速对比,实线为本文完全叠加法计算结果,虚线为有限次叠加计算结果。由图中可看出完全叠加法算出的全时段最大合成振速F(t)max普遍较大。当4列波叠加时最大合成振速差距可达到30.2%。为此针对4列波合成波形进行了对比分析如图10所示。由图10可以看出,按完全叠加方法所得波形最大振速峰值出现稍早,且比按有限次叠加方法所得波形的最大振速峰值高出0.32 cm/s。 图10 两种方法求四列波叠加波形Fig.10 Find superposed waveform of four waves by two methods 图11 振速分量的位置关系对比Fig.11 Position relations comparison of velocity components 参考各列波幅值分量与单孔波形的关系(图11),上面4列波为有限次叠加方法确定的子波,下面四列波为完全叠加方法确定的子波。可以看出:采用有限次叠加方法,由于确定Δt4,3时,Δt3,2、Δt2,1已经固定下来,可调整空间有限,导致第4列波只能以较小峰值g(12) 参与最不利情况叠加,而单孔最大峰值g(4)无法参与贡献,二者幅值差距g(4)-g(12)=0.402 cm/s,是导致两种方法求得正向最大合成振速差距0.32 cm/s的主要原因。 有限次叠加的简化方法限制了各段微差时间共同作用的可能性,可造成叠加结果30%的差异。虽然在一些应用实例中采用简化方法取得成功,是因为第二临空面在60 ms已经出现,微差合成作用受到抑制。但对于其他工程若第二临空面形成时间较长,形成前参与叠加波数多,该方法计算的药量有可能超过安全振速,因此不具有广泛适用性。采用本文完全叠加法穷尽所有可能合成振动后进行爆破设计更为准确。 (1)快速发展的计算机及相关技术展示了解决爆破难题的巨大潜力,有可能给爆破研究方法带来新的变革。如过去因雷管各段均有延时范围并随孔数增加形成海量合成振动组合、导致多孔微差爆破振动计算的难题,本文设计计算程序并采用优化算法,在有限时间完成了8孔微差爆破上百万种以上合成振动计算量,为精准爆破设计奠定了基础,可以预计今后更大数据的计算将在爆破工程中发挥重要作用。 (2)提出了城市隧道低振速精确控制掏槽药量设计的新方法,主要特点是考虑了各段雷管延时起爆误差影响和多孔微差合成振动影响,可表述为:计算第二临空面形成前各段延时范围内所有可能振动曲线后,选择峰值振速不超标的最大药量作为设计掏槽药量;第二临空面形成前逐孔逐段掏槽;形成后多孔同段爆破;第二临空面形成时间因地质条件和爆破参数不同而有差异,可用比较计算合成振动曲线与实测振动曲线间差异获取。 (3)现在施工中常采用以标称段号设计爆破网络,本文以渝中隧道为例研究表明:同段延时误差即使在较小范围内,其合成振速之间差异也可达57%,因此按雷管标称段号设计起爆顺序做法难以做到城区隧道低振速精准控制爆破。 (4)比较过去的有限次叠加法与本文完全叠加法计算的微差爆破最大合成振速曲线,发现采用简化计算最多可造成30%的失真。进一步分析表明:波数量较少时合成峰值取决于单个波形的较大波峰;数量多时取决于处于波峰的子波个数。因此有限次叠加法在第二临空面形成前起爆段数少时计算较准确;起爆段别较多时则不能对该合成振速进行有效折减而误差较大。采用本文方法则穷尽所有延时范围内可能的合成振动,计算结果准确。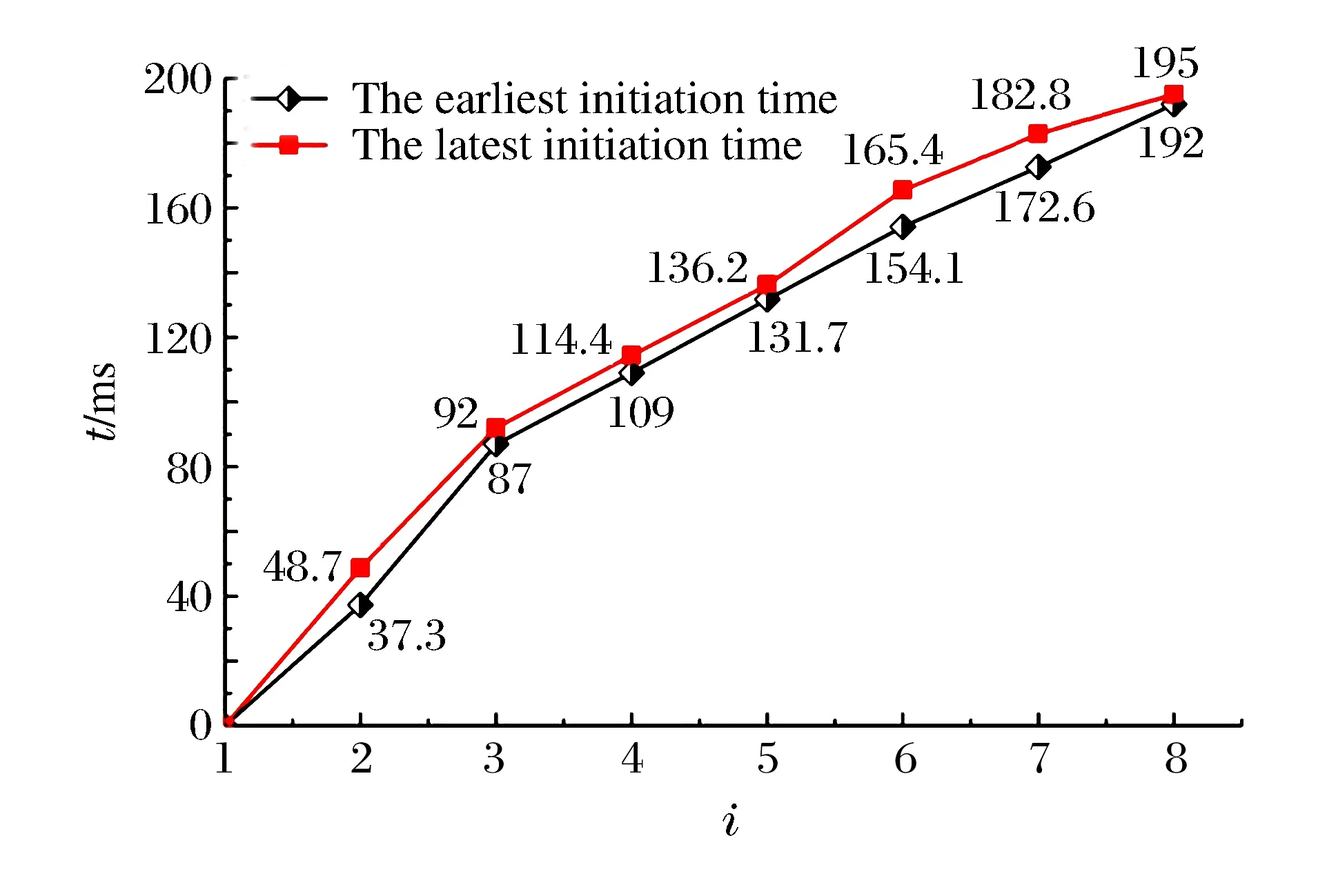
1.2 多孔微差振动合成的原理
1.3 叠加求振速最大值

1.4 计算机用时与程序运行可行性

1.5 结合第二临空面形成时间调整爆破设计
2 振动合成计算实例
2.1 拟合叠加

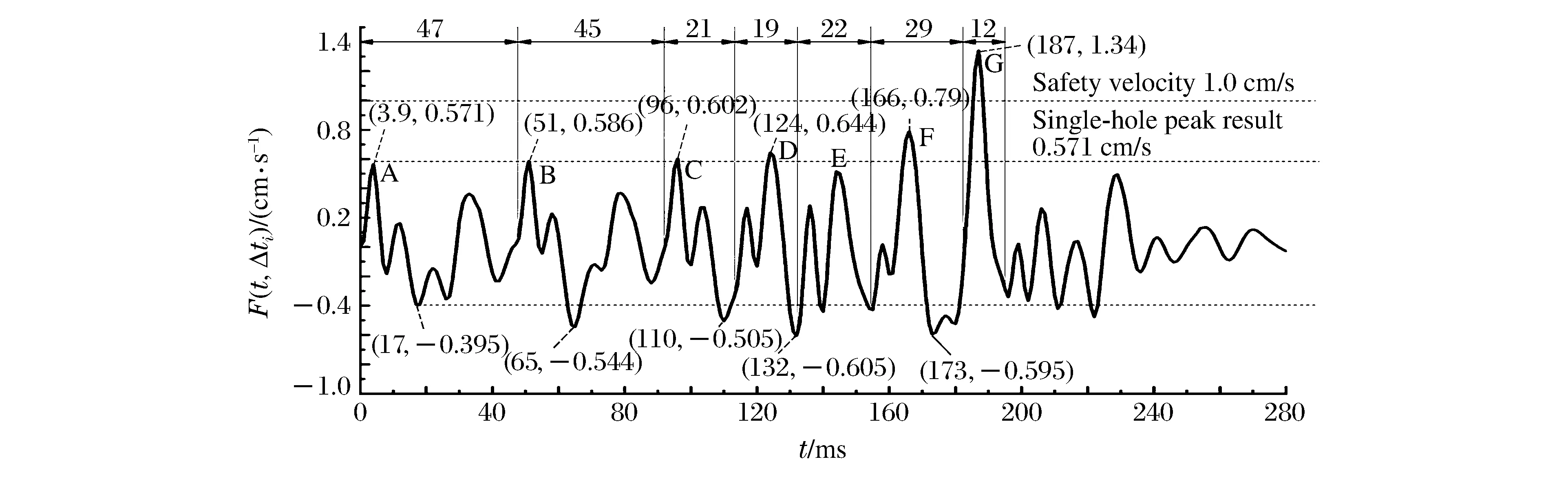
2.2 合成波形分析

3 应 用
3.1 确定第二临空面形成时间
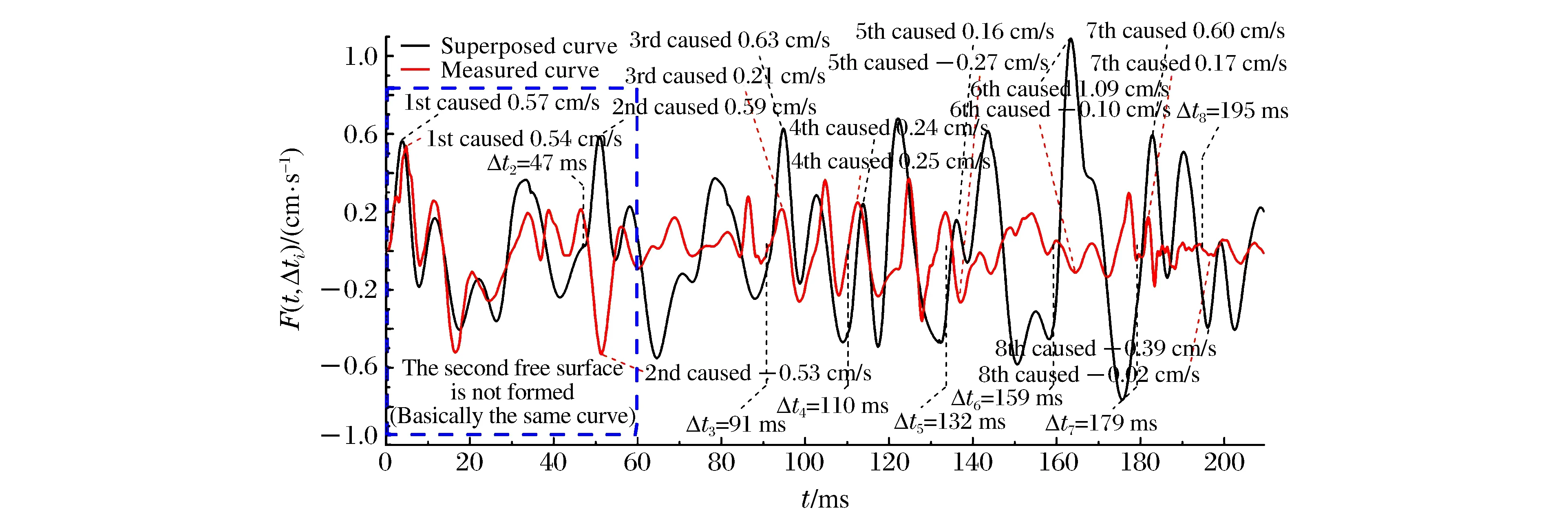
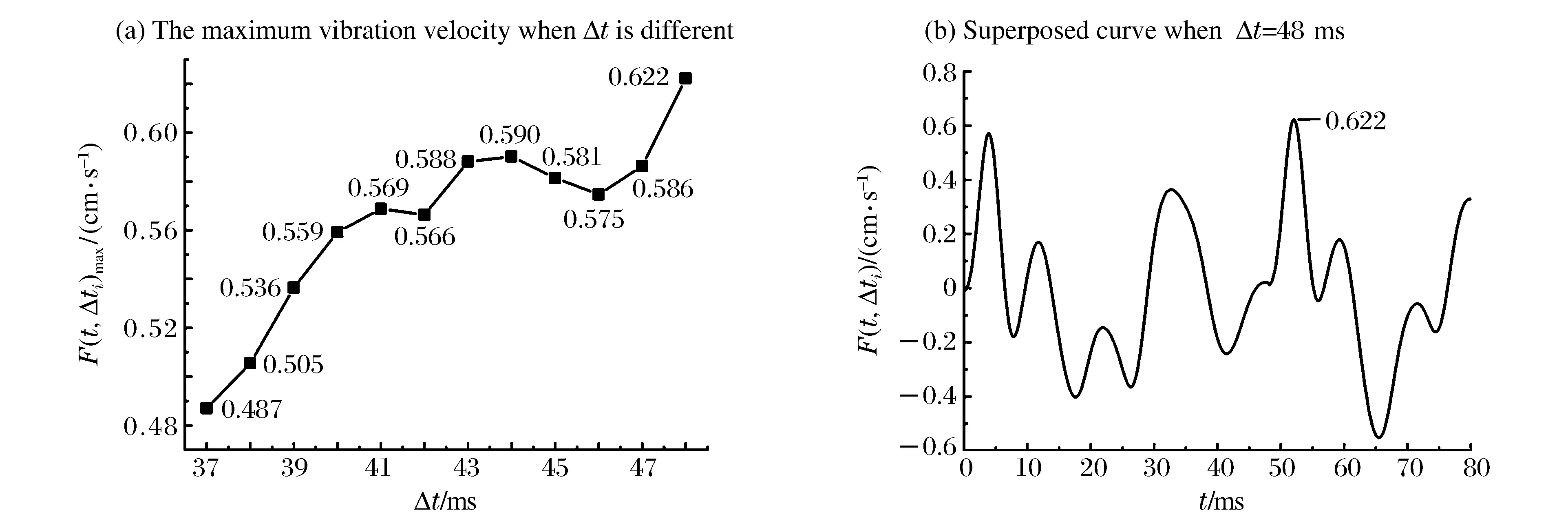
3.2 根据第二临空面形成时间进行爆破药量设计
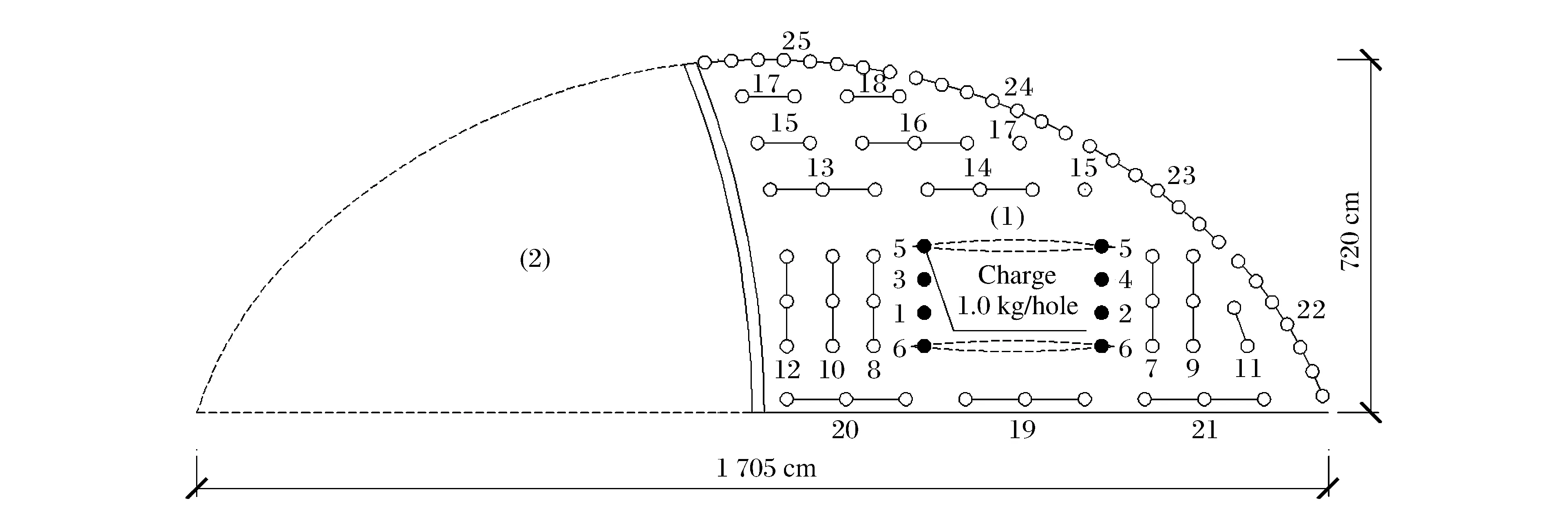
3.3 现场应用
4 两种多孔微差爆破振动合成计算方法的可靠性比较



5 结 论
