融合背景图像信息和多特征压缩的相关滤波跟踪算法

谢雨霏，杨新民，刘晓利，王胜红

（1.南京理工大学瞬态物理国家重点实验室，南京210094；2.淮海工业集团有限公司，长治046000）

0 引言

相关滤波类算法因兼具鲁棒性好、计算量少的特点，在被广泛关注的同时，也在历届视觉目标跟踪（Visual Object Tracking，VOT）挑战赛［1］中有着令人惊艳的表现。

最早将相关滤波用于目标跟踪的是MOSSE算法［2］，该算法采用灰度特征，跟踪速度高达669fps，远远超出了其他算法。CSK［3］在MOSSE的基础上引入了循环矩阵和核函数的概念，该算法虽然也使用灰度特征，但跟踪效果比MOSSE更胜一筹。KCF［4］采用HOG特征，将CSK算法的图像特征通道从单通道扩展为多通道。CN［5］在CSK算法的基础上使用颜色特征替换了灰度特征，并改进了CSK算法的更新机制。DSST［6］主要解决了目标在跟踪过程中的尺度变化问题，可使算法较好地应对目标尺度变化。LCT［7］借鉴了TLD算法中的随机厥分类器，增加了置信度滤波器，能够较好地解决目标遮挡问题。

但是，目前已提出的大部分基于相关滤波的跟踪算法大多忽略了背景图像信息，而背景图像信息在先验知识的获取、跟踪精度的提高等方面均起着十分重要的作用。为充分利用目标背景图像信息，本文在DSST跟踪器的基础上，提出了一种融合背景图像信息的多特征压缩跟踪算法。在数据集 OTB⁃13［8］上进行的跟踪实验结果表明，相对于一些传统跟踪算法，本文提出的改进算法在跟踪精度上有了较大的提高。

1 DSST相关滤波算法简介

DSST是一种可以进行自适应尺度变换的相关滤波类算法，其包括位置滤波器算法和尺度滤波器算法。由于本文工作主要建立在DSST基础之上，因此首先对该算法做出简要介绍。

1.1 位置滤波器

多通道特征的相关滤波器将t帧提取的图像块a0设为d维特征向量，al代表第l维特征，l∈｛1，…，d｝。通过建立最小化代价函数构造最优相关滤波器ht，每个特征维度包含1个滤波器hl。

式（1）可根据 Parseval定理推导得出。其中，∗代表循环运算；hl、al、g均为M×N的矩阵，g为训练样本a的期望输出；λ1为正则项系数，用来消除样本频谱中零频分量的影响，避免式（1）的解出现零分子。

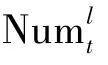
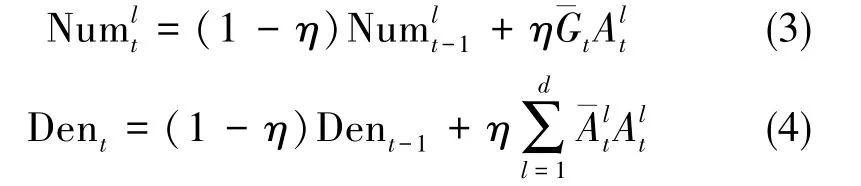
使用式（5）计算（t+1）帧的矩形图像块z的响应得分y，目标位置p可以通过求解相关滤波器的最大响应值得到

1.2 尺度滤波器

DSST算法建立了一维独立的相关滤波器，作为尺度搜索和目标估计的方法。首先以目标位置p为中心，在周围M×N的矩形区域计算一个特征金字塔，然后使用式（3）、式（4）更新尺度空间跟踪过滤器st。滤波器的大小为M×N×S，M和N分别代表滤波器的高度和宽度，S代表尺度变换的数量。

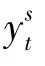
2 融合背景图像信息和多特征压缩的相关滤波跟踪算法

在此简述DSST算法的不足和相应的改进方法。

2.1 背景图像信息融合

相关滤波类跟踪算法背景图像信息利用率低，主要是由两方面因素导致的，为避免跟踪结果出现漂移，搜索范围只有上一帧目标大小的2倍，能利用的背景图像信息很少。为了抑制边界效应而添加的余弦窗，使得背景图像信息再度减少。因此，在面对目标快速运动、遮挡或背景模糊等复杂情况时，相关滤波类算法的跟踪效果并不理想。为了更充分地利用背景图像信息，提高跟踪精度，本文借鉴上下文感知相关滤波器的跟踪算法［9］，以目标为中心，将周围的背景图像信息融入位置滤波器。通过在位置滤波器中添加背景图像信息，可以削弱背景图像信息对滤波器的干扰，进而提高跟踪精度。

在t帧时刻，提取目标a0∈Rn周围的背景图像块ai∈Rn。 此时，新的位置滤波器需满足式（7）

式（8）中，A0∈Rn×n和Ai∈Rn×n分别为a0、ai循环矩阵的形式，k为加入的背景图像块的个数，λ2为对所有背景块加以约束使其归零的正则项。其余部分（如目标检测）与原DSST跟踪求解的过程一致，具体公式推导详见文献［9］。

2.2 自适应融合

本文选择了判别能力强的2种特征对目标的外观进行描述，分别是 CN 特征［5］与 HOG 特征［10⁃11］。

虽然CN特征和HOG特征都能有效提升相关滤波类跟踪器的跟踪性能，但是当背景光照发生剧烈变化时，单独采用CN特征的跟踪器很难有效地从背景中判别出目标。事实上，CN特征与HOG特征是互补的，它们分别为图像的0阶和1阶特征，可以从不同方面对图像进行表达。为了充分发挥2种特征的优势，达到提升跟踪性能的目的，本文在特征融合前首先进行了特征置信度分析。

跟踪结果置信度通常由Fmax判定，定义为

式中，yt为t帧时刻的响应得分图，Fmax为其中最大的响应值。这种指标中的每一帧仅使用了响应得分图中的一个值，缺乏足够的可靠性。为了能够更好地衡量结果的置信度，需引入APCE判据［12］对置信度进行评价，定义为

2.3 特征压缩

特征是影响相关滤波类跟踪算法速度的关键因素。CN特征与HOG特征的结合虽然能在一定程度上提高跟踪精度，但势必会影响算法速度。为了能够在不降低跟踪性能的前提下，在一定程度上提升算法速度，需对位置滤波器和尺度滤波器的特征信息进行降维压缩，将CN特征和HOG特征分别从10维/31维降为4维/18维。

本文还对尺度滤波器进行了压缩，使用压缩尺度滤波器［13］进行了对目标尺度的检测，其基本思路是在计算过程中将尺度层数从DSST算法中的33层降低为17层。在得到压缩尺度滤波器响应结果的Fourier域之后，通过插值方法，将尺度数量从17插值到33，以获得更精确的尺度定位。

2.4 算法流程

本文提出的算法流程具体如下：

输入：图像xt，上一帧目标位置pt-1和尺度βt-1，滤波模型ht-1，尺度模型st-1。

1）在图像xt中，对尺度为βt-1、位置为pt-1的通过循环移位得到的所有候选样本提取（HOG+CN）特征A0（xt，pt-1）；

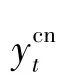
3）根据式（11）得到响应图yt，更新目标位置pt。

式中，Fmax和Fmin分别代表t帧响应图中的最大值和最小值，Fm，n为响应图中第m行、第n列的响应值，mean表示求取平均值。

当且仅当2项指标，即Fmax和APCE都大于其历史平均值的一定比例β1、β2时，认为当前特征可靠，允许进行特征融合。

4）在图像xt中，对尺度为βt-1、位置为pt的各尺度层所有候选样本提取HOG特征；

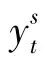
输出：目标的位置pt和尺度βt，更新滤波模型ht，尺度模型st。

3 实验结果与分析

本文在提出了融合背景图像信息的多特征压缩跟踪算法的基础上，根据有关评价指标在OTB标准数据集上验证了该算法的性能。OTB⁃13由51个被标注的视频序列组成，数据集中的序列主要由11种不同挑战性的影响因素构成。本文利用文献［8］中的OPE评价方法，对改进算法的各方面性能进行了分析。

3.1 实验环境及算法参数设置

本文改进算法是在Matlab＆Mex混合编译环境下实现的，计算机的配置为Intel Core i5⁃4300U CPU＠1.90GHz，内存为2.50GB。在算法中，位移滤波器所使用的特征为HOG+CN特征组，尺度层数采用17层。在改进算法中增加的参数如表1所示，位置估计中的其他参数参考DSST算法［6］。

3.2 背景图像信息融合性能分析

选取Subway序列中被遮挡的片段进行背景图像信息融合性能分析，对比如图1所示。从第38帧开始，跟踪目标被遮挡，由于遮挡面积较小，对DSST和改进算法的影响不大，响应图是单峰的。在第39帧时，目标大部分区域被遮挡。如图1（b）所示，DSST的响应图不再是单峰。改进算法加入了背景图像信息，虽然比38帧最大响应值略微降低，但图1（c）中的响应图仍有较高的可信度。当跟踪进行到第40帧时，目标区域完全被遮挡，DSST的响应图持续震荡，Subway序列跟踪失败。改进算法的最大响应值虽然低于38帧峰值，但单峰响应图表明当前跟踪结果可信，图1（a）可以保持稳定跟踪。

图1 背景图像信息融合性能分析Fig.1 Fusion performance analysis of background image information

3.3 与DSST跟踪器的对比分析

对所选取的6组视频序列分别用DSST和改进算法进行了跟踪测试，跟踪效果对比如图2所示。

对改进算法进行定性分析，如图2所示。Bas⁃ketball序列包含目标形变和背景干扰，DSST在跟踪过程中逐渐偏移目标中心，转而跟踪目标局部，而改进算法能够很好地应对这种情况，确保跟踪精度。Couple序列在19帧附近受到目标形变和快速运动的影响，改进算法同样能够有效应对。Freeman1和Panda序列主要出现了尺寸变化、目标平面内和平面外旋转等情况，DSST在Freeman1序列的169帧和Panda序列的400帧附近分别跟丢目标，而改进算法能够有效地持续跟踪。Tiger2和Subway序列主要发生了目标形变和目标遮挡的问题，由于DSST只有HOG特征，没有背景图像信息，所以其分别在108帧和43帧跟踪失败，改进算法可以有效地持续跟踪。

分别对DSST和改进算法的目标跟踪数据做出定量计算，结果如表2所示。

以上6组视频序列表明，中心距离精度平均提高了52.8%，重叠率平均提高了49.3%，中心位置误差最小降低至4.04，Basketball和Subway序列均基本实现了准确跟踪。实验数据表明，改进算法在各方面的性能均更优越。

3.4 与各主流跟踪器的比较

本文采用统一的评价指标将算法与其他7种主流的跟踪算法进行了评价，并在算法中使用了传统的手工提取特征，这些算法包括了CT、TLD、KCF、Struck、DSST 和 fDSST。

如图3所示，在所有参与比较的8种跟踪算法中，本文提出的改进算法在数据集OTB⁃13上的表现最为出色，跟踪精度总体较DSST算法提高了5.3%。对OTB⁃13数据集中涵盖的多种挑战因素进行分析，发现当目标发生平面外旋转、尺度变化或遮挡时，改进算法能够较好地应对，跟踪精度分别提高了5.3%、3.3%和7.8%，相比DSST算法效果提升较明显。

4 结论

本文在DSST框架下，提出了一种融合背景图像信息的多特征压缩跟踪算法。为了提高目标跟踪的精度和鲁棒性，将背景图像信息融入位置滤波器。合并CN颜色特征和HOG特征，通过2种特征分别的位置滤波器响应图最大值及APCE指标实现了自适应的响应融合，提高了模型融合的效率。为提升运行速度，对位置滤波器和尺度滤波器的特征信息进行降维压缩。实验对比分析表明，改进算法提高了跟踪的精度与成功率，在遮挡、形变、尺度变化等情况下均具有较高的鲁棒性，具有重要的理论和应用研究价值。