无人水面艇自适应路径跟踪算法

朱 骋，庄佳园，张 磊，许建辉，苏玉民

（哈尔滨工程大学水下机器人技术重点实验室，哈尔滨150001）

0 引言

在2007年，美国海军发布的《海军无人水面艇主计划》中，给出了无人水面艇（Unmanned Surface Vehicle，USV）定义：静止时浮在水面上，而在运动时持续与水面接触，且具有不同自动操控能力的一种无人航行器。无人水面艇具有巨大的军事和工程应用前景，尤其是在维护国家海洋安全和海洋开发等方面（诸如海洋探测、环境监控、目标侦查、通行中继等）将发挥不可替代的作用。

路径跟踪作为无人水面艇控制系统中最基本的模块，要求船舶不考虑时间约束，在路径规划器计划的期望路径中自动航行。相比航迹跟踪，路径跟踪忽略了时间因素，因此能够更加光顺地收敛到期望路径，且不易出现控制输入饱和现象。Niu等人［1］基于 “C⁃enduro”无人水面艇讨论了4种无模型的路径跟踪方法，包括：胡萝卜追逐法（Carrort Chasing Algorithm）、非线性制导律（Nonlinear Guidance Law）、向量场跟踪法（Vector Field Algorithm）和视线法（Light⁃of⁃Sight），文中结论是 LOS 在长航时相比其他3种算法更具备抗干扰能力。Børhaug等人［2］针对有洋流存在的情况，提出了改进的LOS制导律和自适应反馈控制器，理论分析并证明了该控制策略在恒定和无旋海流的情况下能够保证直线路径的全局渐近跟踪。但是，由于动力学模型中同时存在绝对速度和相对速度，其迫使在推力和转向控制器中引入自适应，增加了算法的复杂性，降低了稳定性。Caharjia等人［3］在 Børhaug的基础上，假定海流恒定且无旋，采用相对速度模型简化了控制系统，实现了系统的全局渐近稳定性和局部指数稳定性。董早鹏等人［4］基于非对称的无人水面艇数学模型，针对非线性反步法和LOS法之间存在的互补优化问题，给出了结合的控制策略，理论分析证明了系统的全局渐近稳定性。

目前，多数LOS导引策略的改进大多基于增强其抗干扰能力，而忽略了船体本身操纵性和规划方案改变造成的影响。比如当无人水面艇在航行时，航行速度的改变或期望航线长度的改变，也会造成超调增加，振荡时间变长，路线跟踪的完成度不高（比如原本设定的安全距离为30m，但目前跟踪路线长度为50m，造成该路径只跟踪了40%）等问题。因此，针对传统LOS制导律［5］无法实时调整参数的问题，以及为了充分利用无人水面艇操作性，提高能量利用率，本文设计了基于Mamdani模块控制的自适应LOS控制策略。

1 欠驱动水面滑行艇模型

假设以下条件成立：

1）只考虑艇体在纵荡、横荡、艏摇的三自由度运动；

2）船舶前后左右对称，并且中心和重心重合；

3）欠驱动，且只安装1个推进泵，通过推进泵的推力和扭转角度控制推力和转艏力矩；

4）忽略风浪流的干扰。

可得如下欠驱动非线性方程［6］

如图1所示，本文通过对 “天行一号”进行模型辨识，得

图1 “天行一号”无人水面艇Fig.1 “Tianxing No.1” USV

阻力系数R的计算如下所示

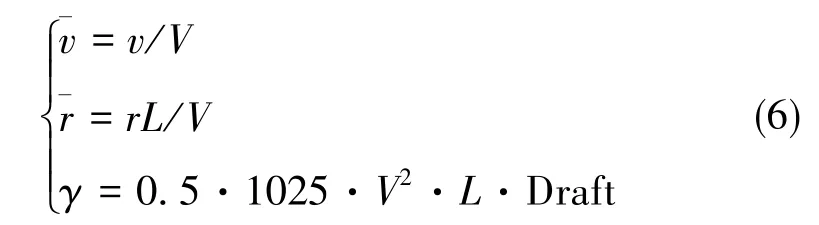
式中，L为艇体水线长，Draft为艇体吃水。

2 问题描述

LOS导引策略作为经典的路径跟踪策略，由于其不依赖于模型，且需要设计的参数少，具备抗干扰能力强等特点，被广泛应用于USV的路径跟踪。作为几何算法应用，可将LOS导引划分为基于收敛圈和前视距离2种［7］。本文以大地坐标系作为惯性坐标系，由图2可知LOS制导律原理。

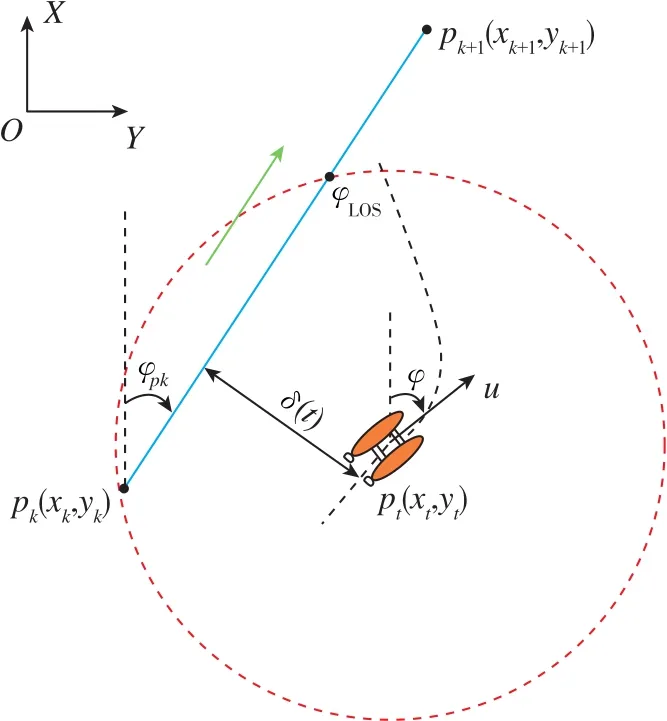
图2 LOS制导律原理图Fig.2 Principle diagram of LOS guidance law

2）LOS导引任务：通过控制船舶的方向始终对准LOS角，引导船舶位置收敛到期望航线，使得横侧偏差δ（t）和目标距离d（t）收敛至原点

3）安全半径RSafe：期望目标点的膨胀系数。当d（t）≤RSafe时，USV到达目标点，进而考虑是否跟踪下一个目标点。

4）LOS制导律：基于LOS导引任务的要求，输入艇体当前位置和期望航线，输出当前时刻期望艏向φd

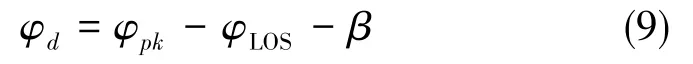
式中，φpk表示期望航线与X轴形成的夹角；β表示横漂角，β=tanh-1（v/u）。

定理1：若航向控制器完美跟踪LOS制导律输出的期望艏向，则横侧偏差δ（t）和目标距离d（t）收敛至原点［8］。

由图2得横侧偏差δ（t）为

对式（10）求导，得

若航向控制器能够完美跟踪期望艏向，即φ=φd，则有

选取V1=δ2/2，将其作为Lyapunov函数，对其求导

根据Lyapunov稳定性定理可知，当USV艏向为期望艏向时（φ=φd），USV的位置能够渐近收敛于期望航线上。LOS导引策略的控制参数：1）安全半径RSafe，判断USV是否跟踪下一个目标点，从而影响横侧偏差δ（t）的超调和航线的跟踪完成度；2）收敛半径R控制δ（t）的收敛快慢，若R越大，δ（t）收敛越慢，反之亦然。

从式（12）可以看出，USV的前向速度u与δ（t）之间存在耦合。如果安全半径固定，当期望航线的距离小于安全半径，则此期望航线被跳过。为避免上述问题，本文采用模糊控制器对LOS的控制参数进行修正，削减了u与δ（t）之间存在耦合的影响并且获得较为优良的航线跟踪完成度。

3 基于Mamdani的无人水面艇直线路径跟踪方法

3.1 直线路径跟踪控制策略

欠驱动系统的内模为自制系统，不受输入控制。本文采取模糊控制器，针对不同的期望速度，通过专家辨识给出不同的LOS控制参数，从而削弱速度对横侧偏差的影响，实现系统的速度 “解耦”。

基于Mamdani的LOS路径跟踪控制器原理框图如图3所示。

LOS制导律模块采用上述提及的制导律。

航速控制器和艏向控制器分别采用累积式PD和PD控制器，产生推进器推力P，以及推进器扭转角度α。

图3 基于Mamdani的LOS路径跟踪原理框架图Fig.3 Block diagram of LOS path following principle based on Mamdani

3.2 模糊控制器设计

本文所采用的模糊控制器为基于Mamdani的MIMO模糊控制器［9］，根据给定的期望速度ud和目标路径（Pk，Pk+1）求出的目标路径长度L，将其作为两个输入变量。ud的基本论域为［0，4］，L的基本论域为［0，500］，两个输出变量分别为LOS导引策略的控制参数安全半径RSafe和收敛半径R。其中，RSafe的基本论域为［0，30］，R的基本论域为[0，100]。 将ud、L、RSafe、R模糊化，模糊集合分别为EU、EL、ES、ER。

R影响δ的收敛速度，当R越大则δ越快收敛，RSafe决定何时进入下一个目标点跟踪。本文给出模糊规则设计的基本原则为：L越大，RSafe越大，R越大；ud越大，RSafe越小，R越大。具体如表1所示。

表1 模糊集合Table 1 Fuzzy set

建立推理规则库，如表2所示。表格内，行代表EL，列代表 EU； （x，y）中，x代表ES，y代表ER。

表2 模糊推理规则库Table 2 Rule base of fuzzy reasoning

4 仿真实验

为验证本文算法的优越性和有效性，实验采用不规则且分段速度不同的闭合曲线作为期望航线，同时与ud∈（1.0，2.5）、路线长度 Length∈（100，300）之内具有优良跟踪精度的LOS控制参数RSafe及R（RSafe=20、R=30）进行对比。

USV从原点出发，初始速度u=0，初始艏向φ=0，期望路径点pn（x，y）分别为p1（55.7，45.6）、p2（55.7，228.0）、p3（167.0，319.2）、p4（612.3，319.1）、p5（55.7，45.6）。

跟踪时的期望速度如下：up0，1=1.5、up1，2=2.5、up2，3=4.0、up3，4=3.5、up4，5=2.5。

水动力参数如下：Yv=-0.4715、Yr=0.07156、Nv=-0.1459、Nr=-0.0557；Xvr=-0.0025、Xvv=0.0682、Xrr=0.0039、Yvr=-0.29、Yvv=-0.4757、Yrr=-0.035、Nvv=0.0148、Nrr=-0.04。

船型参数如下所示：L=5.2、Draft=0.4、Mass=500.5、IZ=8000、Mxx=184.57、Myy=15.3384、Mrr=1206。

控制器参数如下：Ku=1、kPu=10、kDu=3、kPα=9、kDα=6。

路径跟踪结果对比如图4所示。

从图4（a）可知，模糊LOS的全局跟踪精度更高。从图4（b）和图4（c）可知，在跟踪第一、第二段路径时，模糊LOS的最大超调为0.7，没有发生振荡，传统LOS的最大超调为1.1，发生了一次振荡，两种算法跟踪效果均十分良好。从图4（d）可知，在第三段路径初始阶段，即在第二、第三段路径拐角处，模糊LOS的最大超调为2.1，发生一次短暂的振荡，传统LOS的最大超调为4.9，发生两次振荡。从图4（e）可知，在第四段路径初始阶段，即在第三、第四段路径拐角处，模糊LOS的最大超调为10.5，不发生振荡，传统LOS的最大超调为14.4，发生了一次振荡但收敛时间较长。

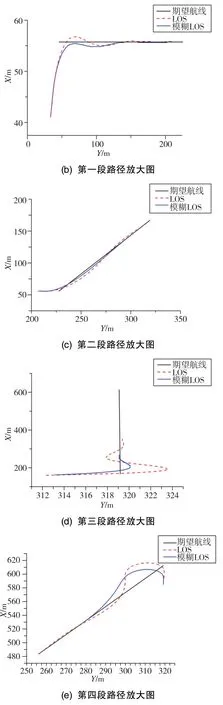
图4 基于Mamdani的LOS和传统LOS闭合曲线跟踪图Fig.4 Closed curve path following of different LOS

对比可得，基于Mamdani的模糊LOS导引策略能够更快地收敛于期望航线，且能够更加精确地跟踪期望航线。

具体跟踪精度如图5所示。

图5 控制参数变化及横侧偏差Fig.5 Varying of parameters and cross-track error

从图5可知，在航线或者航速变化时，模糊LOS通过自适应的调节参数，使得横侧偏差的震荡时间减小，最大超调减小（排除由于切换目标点而产生的跃变），平均误差减小，整体跟踪精度更高，并且模糊LOS能够更快地完成路径跟踪。具体数值如表3所示。

表3 跟踪精度Table 3 Path following accuracy

推进器使用及控制跟踪曲线如图6所示。

从图6可知，两种算法的艏向跟踪相差不大，但是跟踪时间为600s～700s时，传统LOS产生的超调及振荡时长远大于模糊LOS；在1200s左右，传统LOS的响应速度远慢于模糊LOS，从而导致后续跟踪完成时间慢于模糊LOS。

图6 控制器性能图Fig.6 Diagram of controller performance

通过分析可知，由于模糊LOS削减了纵向速度u和LOS导引策略之间的耦合影响，因此其速度控制振荡时间较短，收敛速度更快。从图6（c）可知，无论是推进器推力还是扭转角度，模糊LOS的超调均更小，振荡时间更短。因此，其更有效地利用了艇体操纵性能，能量利用率更高。

5 结论

本文研究了欠驱动无人水面艇的路径跟踪问题。首先给出了水面滑行艇的数学模型，然后通过Lyapunov定理证明了LOS算法的稳定性，最后采用模糊控制的方法修正了LOS控制参数。

通过仿真实验对比传统LOS算法，验证了基于Mamdani的LOS导引策略的优越性和可行性。仿真数据表明，该算法能够精确地跟踪不规则闭合曲线，相比传统LOS具有优良的自适应能力、更好的鲁棒性，推进器效率更高，并且将模糊控制作为智能算法，使其相比传统算法更具备先进性。同时，本算法作为无模型算法，在应用上具备普适性。

为了真实地反应USV的实际操纵情况，并让算法具备更加优秀的泛化能力，下一步将基于假设船前后不对称、且受到海洋环境干扰的情况下，研究将智能控制理论及多种控制方法结合的算法。