Identification of the state-space model and payload mass parameter of a flexible space manipulator using a recursive subspace tracking method
2019-02-27ZhiyuNIJinguoLIUZhigngWUXinhuiSHEN
Zhiyu NI,Jinguo LIU,*,Zhigng WU,Xinhui SHEN
aState Key Laboratory of Robotics,Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,China
bState Key Laboratory of Structural Analysis for Industrial Equipment,School of Aeronautics and Astronautics,Dalian University of Technology,Dalian 116024,China
Abstract The on-orbit parameter identification of a space structure can be used for the modification of a system dynamics model and controller coefficients.This study focuses on the estimation of a system state-space model for a two-link space manipulator in the procedure of capturing an unknown object,and a recursive tracking approach based on the recursive predictor-based subspace identification(RPBSID)algorithm is proposed to identify the manipulator payload mass parameter.Structural rigid motion and elastic vibration are separated,and the dynamics model of the space manipulator is linearized at an arbitrary working point(i.e.,a certain manipulator configuration).The state-space model is determined by using the RPBSID algorithm and matrix transformation.In addition,utilizing the identified system state-space model,the manipulator payload mass parameter is estimated by extracting the corresponding block matrix.In numerical simulations,the presented parameter identification method is implemented and compared with the classical algebraic algorithm and the recursive least squares method for different payload masses and manipulator configurations.Numerical results illustrate that the system state-space model and payload mass parameter of the two-link flexible space manipulator are effectively identified by the recursive subspace tracking method.
KEYWORDS Flexible space manipulator;Linearization;Parameter identification;State-space model;Subspace methods
1.Introduction
In on-orbit servicing missions,a space manipulator is an important component of a spacecraft structure that is widely applied for space object capture,space structure assembly,and even on-orbit structure identification.1-3In order to reduce the launch mass and increase the workspace,the design of a space manipulator is generally lightweight and long-span,so structural vibrations are caused while manipulating large payloads due to the microgravity environment.Thus,oscillations may become evident even with an extremely slow motion.4Consequently,some necessary control technologies must be employed to suppress structural vibrations.In this situation,on-orbit identification technology is an effective approach to obtain new system properties after a capturing process,which has been successfully implemented in certain on-orbit spacecraft.5-7On-orbit identification of structure parameters can not only be used for the controller design to decrease a manipulator's oscillation during movement,but also effectively monitor system operating conditions to ensure on-orbit safety.8In particular,if a target captured by using a manipulator is a non-cooperative object with an unknown property,then accurate identification of unknown object parameters may overcome system uncertainty and provide an important reference for modifications of attitude and vibration controller parameters.9-12
A manipulator's system model and corresponding dynamics parameters might be changed due to variations in the manipulator configuration and payload mass.Therefore,the corresponding system identification issues become more sophisticated.This study mainly focuses on the identification problems of a space manipulator's state-space model and payload mass parameter in a fixed configuration,and subsequently the system model and dynamics parameters are only affected by changes in the payload mass.Consequently,the original nonlinear dynamics equation can be degraded as a linear model by the local linearization technology,and thus the corresponding system can be considered as linear and time varying due to changes in the endpoint payload mass during a space capturing process.
Identification of a manipulator model and payload inertia parameter has been performed in other studies.Based on the subspace method,Liu et al.13identified a state-space model of a single-link flexible manipulator through experiments,and developed a new procedure to implement model reduction and improve model accuracy.Based on the optimal experiment design,the dynamics model identification of six-degree of freedom parallel robots using the maximum-likelihood estimator was discussed in Ref.14.Furthermore,to deal with the strong non-linear behavior of a manipulator system,a state-space model identification approach based on a linear parameter varying system was proposed,and a set of experiments with different configurations was performed by Mercere et al.15For the manipulator inertia parameter identification,momentum conservation and least-squares estimation are commonly applied to identify system and payload inertia parameters.16-18Liu et al.19presented a recursive differential evolution algorithm to identify the inertial parameters of an unknown target,and the friction parameters of space manipulator joints were revised simultaneously.Cambera et al.20identified the payload mass parameter of a single-link flexible manipulator based on the algebraic identification method.Nevertheless,several aforementioned studies only considered the manipulator as a completely rigid structure and neglected to take into account the influence of flexible vibration.5,16-19,21
System excitation and measurement modes are limited in the space environment,and thus many parameter identification approaches are not suitable for flexible space structures.The subspace algorithm has been proven as an effective method to identify state-space models and corresponding modal parameters.22-24The method can determine the system order and requires little prior knowledge.However,few studies involving the subspace algorithm have investigated the identification of manipulator inertia parameters.The classical subspace method based on singular value decomposition(SVD)requires a high computation cost and is not suitable for online tracking.Therefore,a recursive subspace algorithm was proposed to track system parameters in real-time.25For the space manipulator,an online identification procedure can be implemented to recalculate uncertain parameters periodically,and conveniently update the certainty equivalence controller with unexpected parameter variations.Thus,the recursive identification algorithm is highly suitable for cert a in control approaches that require online updating of the controller parameter such as self-adaptive control.26The identified state-space model and dynamics parameters can also be used for controller correction and to improve the robustness of a control system.However,identification results using the classical recursive subspace algorithm may be affected when the noise signal is strong in a system.To reduce the influence of noise,a recursive algorithm called recursive predictor-based subspace identification(RPBSID)is employed in this study.27Compared with classical recursive algorithms,adaptive filter technology is applied in the RPBSID algorithm to improve the noise immunity,and autoregressive predictors are also used to provide an asymptotically consistent estimate.
In this paper,considering a situation in which an unknown object is captured by a space manipulator,the identification of the manipulator state-space model is studied by using the RPBSID algorithm,and a payload mass parameter estimation approach based on the recursive method is proposed.By establishing the corresponding coupling nonlinear dynamics equation and linearizing at an arbitrary working point,the statespace equation is reconstructed,and system model matrices can be determined by the RPBSID algorithm.Furthermore,using the identified system state-space model,the endpoint payload mass parameter can be derived by extracting the corresponding block matrix.In practical applications,when the system state-space model at the selected working point is identified,the system modal parameter as well as the payload mass parameter can be obtained during the process of capturing the unknown object by using the proposed method,and the identified state-space model can also be applied to modify the system model and controller parameter.For different payload masses and manipulator configurations,the accuracy of the identified system state-space model is verified by a comparison of system test responses,and the payload mass identification results of the proposed method are also compared with those of the classical algebraic algorithm and recursive least squares method.Finally,a simple finite element model is also established,and the corresponding I-O signals are used to identify the payload mass parameter.Numerical results demonstrate that the proposed method is effective in the identification of the model and payload mass parameter of the flexible space manipulator.
The contents of this paper are organized as follows.Section 2 presents the dynamics model of a two-link flexible space manipulator using the Lagrange method,and then the nonlinear dynamics equation is linearized for low vibrations and can be further expressed as a block matrix form.In Section 3,the RPBSID algorithm is briefly introduced to determine the system state-space model,and similarity transformations of different state-space model parameters are reviewed.In addition,a new payload mass identification method is proposed based on the RPBSID algorithm.Section 4 is dedicated to the analysis and comparison of numerical results.Conclusions and future work are presented in Section 5.
2.Dynamics model of a two-link flexible space manipulator
In this section,the nonlinear dynamics equation of a two-link flexible manipulator is established using the Lagrange method.Moreover,the nonlinear dynamics model is linearized at a certain working point and rewritten as a block matrix form.
2.1.Nonlinear dynamics equation of a two-link flexible manipulator using the Lagrange method
Prior to establishing the two-link space manipulator model,the following assumptions are applied in modelling.(1)The links comply with the Euler-Bernoulli beam theory,and the axial deformations as well as the nonlinear geometric effect due to bending are negligible.(2)The two-link manipulator moves in a plane.(3)The cross-sectional area of each link remains constant along the link,and the material is homogeneous,i.e.the linear density and Young's modulus of the links are constant.(4)The influence of gravity on the total system is negligible due to the microgravity condition.(5)To simplify the discussion,this study does not consider joint flexibility.(6)The joints and endpoint payload are simplified as a particle,and the damping of the system is negligible.
Based on the above assumptions,the manipulator coordinate system and corresponding parameters are defined as follows.The originOof the inertial coordinate frameO-XYZis selected at the first joint.The originsO1andO2of the coordinate framesO1-x1y1z1andO2-x2y2z2are selected at the first and second joints,respectively,and the two coordinate frames are attached to theith link.The rotation of theith link coordinate frame with respect to the inertial coordinate frameOXYZis defined as θi(i=1,2).The torques of joints 1 and 2 are defined as τ1and τ2,respectively.In addition,the length,mass per unit length,Young modulus,and second moment of area of theith link are denoted asLi,ρi,Ei,andIi,respectively.The mass of theith joint ismi.The original mass of the endpoint prior to capture is denoted asmo,and the payload mass of the captured object requiring identification is Δm.Therefore,the total endpoint mass(including the original and payload masses)ismo+Δm.A simplified model of the two-link flexible space manipulator is shown in Fig.1.

Fig.1 Planar two-link space manipulator model with a payload object.
Subsequently,the position vector ri(i=1,2)at any point of theith link can be denoted as follows:

wherewi(xi,t)is the lateral deflection of theith link.Based on the assumed mode shape method,each link's lateral deflection can be decomposed as follows:

where φij(xi)and ηij(t)denote thejth mode shape function and thejth modal displacement for theith link,respectively.Furthermore,κ is the number of mode shapes used to model the lateral deflection of theith link.For simple and convenient equation derivation, κ is given as κ =1,i.e.only the first order mode shape is selected for each link.In addition,the mode shape function φ (xi)=(i=1,2)is selected.
i1
Based on the Lagrange method,the total kinetic energyTof the space manipulator is given as follows:

whereTL,TJ,andToare the kinetic energies associated with the two links,joint 2,and the original endpoint mass,respectively.The detailed descriptions ofTL,TJ,andToare given as follows:

where riedenotes the end position vector of theith link.Different from a manipulator on the ground,the influence of gravity on the system dynamics model is negligible for the space microgravity environment,and the geometric effect with respect to the shear and axial deformations is also neglected.Therefore,the potential energyVof the system that is only due to the flexibility of theith link is given as

Based on the Lagrange functionL=T-V,the generalized coordinate q of the system is selected as q= [θ1,θ2,η11,η21]T,and the generalized force Q of the system is given as Q= [τ1,τ2,0,0]T.Subsequently,based on Hamilton's principle,each generalized coordinate qishould satisfy the following Lagrange equation:

Then,the system dynamics equation can be expressed as follows:

where M(q(t)),E(q(t),(t)),and K denote the system mass,coupling coefficient,and stiffness matrices,respectively.The detailed elements of these matrices are provided in Appendix A.Eq.(7)is clearly nonlinear.In this study,only the manipulator parameter identification at a certain working point is considered,and thus the nonlinear Eq.(7)is linearized in the following section.
2.2.Local linearization of the nonlinear model at a selected working point
As mentioned in the previous section,this study only considers the space manipulator parameter identification problem at a certain working point.Therefore,based on the local linearization theory,28Eq.(7)can be linearized at a selected working point as follows:

Thus,the linearized dynamics equation of the space manipulator at the working point is determined and can be used for modal and payload mass identification.It should be noted that the linearization equation is only used near the selected working point.
2.3.Block description of the linearized dynamics equation
The linearized dynamics Eq.(8)includes the rigid body motion with angle δθ and flexible vibration with modal coordinate δη.It is assumed that the modal coordinatesat the working point are extremely low,and thus the corresponding items can be removed from matrix M|(q)0.In addition,based on this assumption,the values of matrices CE,KM,and KEare also significantly low,and subsequently these matrices are omitted in Eq.(8).Let δθ = [δθ1,δθ2]Tand δη = [δη11,δη21]T,and thus the mass matrix M|(q)0and the stiff matrix K can be simplified and partitioned as follows:

where

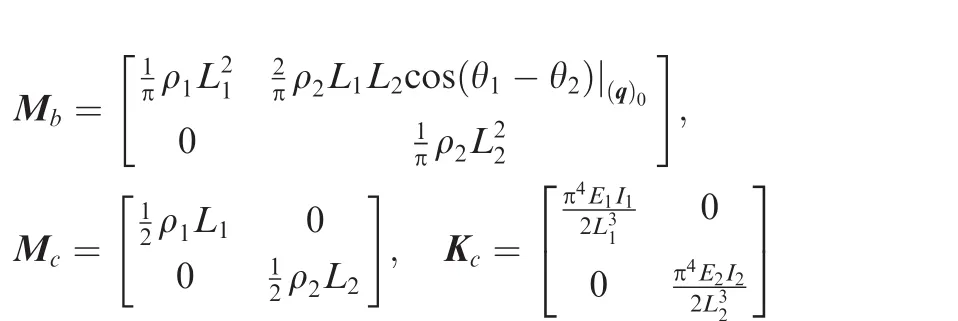
Then,Eq.(8)can be simplified and rewritten as the following two equations:

where u(t)= [τ1(t),τ2(t)]Tis the input vector.Substituting Eq.(14)into Eq.(15),the manipulator vibration equation by using the block matrix form is expressed as follows:

For a manipulator system such as that in Eqs.(14),(15),based on the definition in Section 2.1,when a payload mass Δmof an unknown object is captured at an arbitrary time instant(defined ast=tcap)at a fixed working point,the total endpoint massmpfollowing the capture is defined asmp=mo+Δm,wheremois the original endpoint mass.From the form of mass matrix M|(q)0in Eq.(12),it should be noted that only matrix Maincludes the payload term Δm,i.e.only the value of Machanges for the fixed working point during the entire capturing procedure.Therefore,matrix Mabefore and after capturing can be defined as follows:
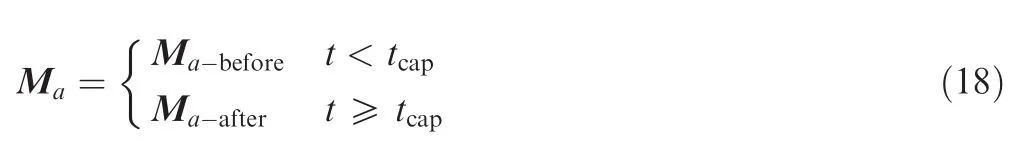
where


Matrix Ma-beforebefore the capturing process does not include the unknown payload parameter Δm,which must be identified,and thus can be considered as a priori knowledge.If matrix Ma-afterat each time instant after the capture process is determined,then the payload mass Δmcan be estimated by calculating the difference between Ma-beforeand Ma-after.In the following section,how to identify the mass matrix Ma-afterfor each time instant will be discussed.
3.Identification of the system state-space model and payload mass parameter
In this section,the block dynamics equation is rewritten as a state-space form,and the recursive procedures of the RPBSID algorithm are briefly introduced to determine the system statespace model and corresponding modal parameters.Moreover,a new method is proposed to estimate the payload mass parameter.Finally,the identification procedures of the statespace model and payload mass parameter are summarized.
3.1.Identification of system state-space model parameters by the RPBSID algorithm
We define a new state vector x(t)=and rewrite Eq.(16)as the following state-space form:

where the vector y(t)is anm× 1 system output that contains angle θiand lateral deflectionwifor each link.Furthermore,Ac,Bc,C,and D are then×nsystem,n×rinput,m×noutput,andm×rdirect transmission matrices,respectively,of the continuous system as follows:

where I is a unit matrix.To simplify the computation procedure,the output matrix C in Eq.(21)is directly given as a unit matrix,that is,the modal displacement δηi1(i=1,2)in the state vector x(t)is considered as the output signal in the following simulations.However,in practical applications,the modal displacement δηi1must be multiplied with the corresponding modal matrix(defined as Φ)to obtain the actual displacementwi(xi,t)of each link in which matrix Φ can be obtained by finite element analysis.
The manipulator's frequency values are derived from the eigenvalues of matrix Ac.Furthermore,considering the influence of noise signal,the discretized innovation forms of Eqs.(19)and(20)can be described as follows:

where e(k)and K(k)denote the white innovation sequence and the Kalman gain matrix,respectively.In addition,A and B are the discretized system and input matrices,respectively.
For the system described in Eqs.(22)and(23),we define a past window denoted bypand a future window denoted byf,in whichp≥f≥n/mis required to ensure that vector autoregressive with exogenous(VARX)parameters can be solved by using the least squares method.In this case,the stacked vectors for input u(k)are defined as follows:

and the stacked vectors ¯y(k-p), ¯y(k+f), ¯e(k-p),and¯e(k+f)are defined in a similar manner.Furthermore,the stacked matrices U(k)and¯U(k)for input u(k)can be defined as follows:

and the stacked matrices Y(k)and¯Y(k)are defined in a similar manner.Subsequently,we define a one-step-ahead VARX predictor as follows:

where superscripts (·)(u)and (·)(y)denote the relations with input u and output y,respectively.The VARX parameter matrices Ξ(u)and Ξ(y)in Eq.(26)are described as follows:

Based on Eqs.(27)and(28),a VARX parameter matrix Ξ
can be defined as follows:

If the system is deadbeat,Eq.(26)can be rewritten in the following linear regression form:

where δ(k)= [¯uT(k-p),uT(k),¯yT(k-p)]T.Based on the adaptive filter theory,the recursive update of matrix Ξ(k)can be implemented as follows:

where Z(k)is the error covariance matrix.Generally,the initial value of Z(k)is given as Z(0)= (1/α1)I,and the parameter α1> 0 is selected to ensure that the recursive problem is well conditioned.Moreover,the following iteration update form for matrix Z(k)is used by the recursive least squares(RLS)filter:27
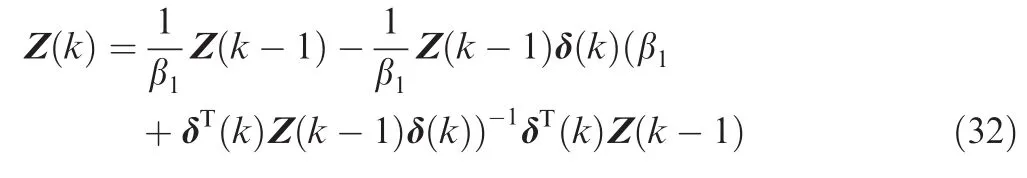
where the forgetting factor β1satisfies 0 ≪ β1≤ 1.Subsequently,two VARX parameter matrices,P(k)and Q(k),are defined from matrix Ξ as follows:

Thus,the state vector x(k)can be obtained from the stack vectors¯u(k-p)and ¯y(k-p)and the VARX parameter matrices P(k)and Q(k)as follows:

where matrix S should be selected as a row full rank to ensure that the recursive computation of the state vector x(k)is stable and convergent.When the state vector x(k)is obtained by Eq.(35),Eqs.(22)and(23)can be rewritten as

The recursive forms of matrices Θ(x)(k)and Θ(y)(k)can be obtained by using the RLS filter,and the detailed recursive forms are directly given as follows:27,29

where

The initial values Δ(0)and Π(0)are similar to Z(0),and are typically selected as Δ(0)= (1/α2)Iand Π(0)= (1/α3)I,respectively,where the parameters α2and α3should satisfy α2> 0 and α3> 0.In addition,the forgetting factors β2and β3in Eqs.(40)and (41)still require 0≪ β2≤ 1 and 0≪β3≤1,respectively.
The detailed derivation procedures of the RPBSID algorithm are also provided in Ref.27The recursive procedures of the RPBSID algorithm are briefly summarized as follows:
(a)Update the VARX parameter matrix Ξ(k)by using Eqs.(31)and(32),where the initial value Ξ(0)of matrix Ξ(k)can be selected as Ξ(0)=Y(0)[¯UT(0),UT(0),¯YT(0)]T.
(b)Construct matrices P(k)and Q(k)from matrix Ξ(k)by using Eqs.(33)and(34).
(c)Estimate the state vector x(k)by using Eq.(35).
(d)Recursively compute the parameter matrices Θ(x)(k)and Θ(y)(k)by using Eqs.(38)-(42),where the initial values are Θ(x)(0)= [In,In×r,In×m]and Θ(y)(0)= [Im×n,Im×r].
When matrices Θ(x)(k)and Θ(y)(k)are determined for each time instant,matrices A(k),B(k),C(k),D(k),and K(k)can be computed by extracting the corresponding block matrix of Θ(x)(k)and Θ(y)(k).Comparing with the frequently-used recursive method based on projection subspace estimation,the adaptive filter is applied in the RPBSID algorithm to overcome the noise influence,and the VARX predictor is also employed to provide an asymptotically consistent estimate.Therefore,the RPBSID method not only provides an unbiased state estimation,but also increases the noise resistance ability.
If the system matrix A(k)is derived,then the modal parameter identification of the system can be implemented.The eigenvalue decomposition of the system matrix A(k)at sampling timekis as follows:

where Λ(k)is the diagonal eigenvalue matrix,and ∑(k)is the corresponding time-varying matrix of eigenvectors.Specifically, Λ(k)=diag(λ1(k),λ2(k),...,λn(k)),in which λj(k) (j=1,2,...,n) contains time-varying conjugate complex eigenvalues. Thejth pseudo-eigenvalue is λj(k)=exp(-ζj(k)Δt± iωj(k)Δt),in which-ζj(k)and ωj(k)are referred to as thejth pseudo-damping ratio and the pseudo-damped natural frequency,respectively;Δtis the sampling time,andi=
3.2.Similarity transformation of the identified state-space model
The RPBSID algorithm is used to obtain a set of the discrete state-space modelin which superscript ‘∧'denotes the identified values that are distinguished from the original values.Although the two statespace modelsand {A,B,C} have the same system input and output(I-O)relationship,their detailed element values,such as those of matrices^A and A,differ.In other words,a system includes an infinite set of the state-space model{Ai,Bi,Ci} (i=1,2,...,∞).Therefore,when a set of the state-space model is identified by the RPBSID algorithm,if one needs to estimate the detailed elements for the original state-space model,then a similarly transformation should be firstly performed between the original and identified statespace models by using a transformation matrix to obtain the original model parameters {A,B,C} (some references also refer to this transformation as ‘topologically equivalent'or ‘coordinate transformation').30,31In this case,the identified and original state-space models satisfy the following relationships:

in which T is the transformation matrix.To obtain matrix T,we assume that the original input matrix C is known(since C can generally be obtained by certain prior knowledge or finite element analysis).Subsequently,T=,in which superscript ‘†” denotes the Moore-Penrose inverse(pseudo inverse).Thus,from Eq.(44),the original matrix parameters{A,B,C} can be obtained and transformed into the continuous system model{Ac,Bc,C}.
3.3.Payload mass estimation by using the identified state-space model
When the state-space Eqs.(22)and(23)are established,the identified state-space modelcan be obtained using the RPBSID algorithm,as discussed in Section 3.1.Furthermore,based on the theory in Section 3.2,the original statespace model{A,B,C} can be determined by using the similarity transformation of Eq.(44),and the corresponding continuous-system model{Ac,Bc,C} is obtained.
When the original matrices Acand Bcare identified,the corresponding block matrices--1Kcand-can be extracted from Acand Bc,respectively,as follows:

where Ac(1:n,:)(or Ac(:,1:n))denotes the firstnrows(orncolumns)of matrix Ac.The elements of Kconly include the Young modulusEi,second moment of areaIi,and lengthLiof theith link,and thus these relevant values are known and remain unchanged during the capture process of an unknown object.Consequently,matrix Kccan be regarded as a priori knowledge.In addition,matrices~M and Ac(n/2+1:n,1:n/2)are both square and full rank.Therefore,matrices~M andcan be computed as follows:


Substituting Eq.(48)into Eq.(49),matrix Mbcan be expressed as follows:

When matrix Mbis computed,matrix Ma(i.e.matrix Ma-after)can be obtained from Eq.(17)as follows:

where the dimensions of Mbshould also satisfy the condition that its pseudo inverse is unique.Subsequently,matrix Ma-afterin Eq.(18)at each time instant can be computed by Eq.(51),and thus the payload mass parameter Δmis determined as follows:

where notation ‘tr” denotes the trace of a matrix.
In Eq.(2),only the first modal displacement for each link is selected in the model,i.e.κ=1,and this system model contains two angle variables {θ1,θ2} and two modal displacements {η11,η21}.Consequently,the block matrices Ma,Mb,and Mcin Eq.(12)are all non-singular square matrices,and the corresponding inverse matrices always exist.However,the number of modal displacements κ must be κ > 1 in most situations,and thus Mbandtypically correspond to non-square matrices,so the corresponding pseudo inverse matrices must be solved.
For the two-link manipulator,if the number of modal displacements is κ > 1 for each link,then the number of columns in matrix Mbevidently exceeds the number of rows.Therefore,for the procedures which require computation of the pseudo inverse,such as Eqs.(50)and(51),the pseudo inverse matrix must be unique.In general,if the number of links is higher(such as three or more),because the dimensions of the identified matrix Ma(namely,Ma-after)are determined by the number of angle variables θ,then the corresponding pseudo inverse matrices for Mbandare ensured as unique only if κ ≥ θ.Therefore,this method can be applied to uniquely determine matrix Mafor different θ and η.
3.4.Summary of identification procedures
The identification procedures for the system state-space model and payload mass parameter in this paper can be briefly summarized as follows.
Step 1:The block matrix form Eq.(16)of Eq.(8)can be rewritten and discretized as Eqs.(22)and(23),and thus the identified state-space model parametersare determined by using the RPBSID algorithm described in Table 1.
Step 2:The discrete model matrices A(k)and B(k)are determined by using the similarity transformation in Eq.(44).Subsequently,the corresponding original state-space model parameters Acand Bccan be calculated.
Step 3:Matricesandare determined using the state-space model parameters Acand Bcfrom Eqs.(47)and(48),and thus matrix Mbis expressed using Eq.(50).
Step 4:Matrix Ma-afteris determined from Eq.(51),and then the payload mass Δmcan be identified by Eq.(52).
4.Numerical simulations
In simulations,a two-link space manipulator model is established,and the appropriate I-O signals are selected for identification.Subsequently,the state-space model matrices of the manipulator at a selected working point are determined by using the RPBSID algorithm.Furthermore,the payload mass parameter is identified using the presented approach,the recursive least squares method,and the algebraic algorithm.20,32,33Finally,a simple finite element model is established,and the corresponding I-O signals are extracted to identify the payload mass parameter using the proposed method.
4.1.Simulation parameters
The structural parameters of the manipulator are listed in Table 2,and the system working point (q)0=[(θ1)0,(θ2)0,(η11)0,(η21)0]is selected as (θ1)0=60°,(θ2)0=45°,and (η11)0= (η21)0=0.In order to ensure that the manipulator's motion is near the working point,the input torque is designed as a square signal.The input torques of joints τ1and τ2are shown in Fig.2.

Table 1 Physical parameters of the two-link flexible manipulator for simulations.

Table 2 Average relative errors of frequencies at different working points using the RPBSID algorithm.
Assume that an unknown object Δm=20 kg is captured when the timetcap=3 s.In simulations,the measurement noise is a stationary zero-mean Gaussian random noise,and the SNR is selected as 40 dB.Then,the corresponding system responses about rotation angles δθ and modal displacements δη can be computed,as shown in Fig.3,where it is observed that the rotation angle and vibration amplitude are small(the angle is less than 3°),and thus the original nonlinear dynamics equation can be linearized.Next,the designed input torques and computed system responses are employed as I-O signals to identify the system state-space model and the corresponding payload mass,in which the parameters of the RPBSID algorithm in Table 1 are selected asp=10,f=5,α1,2,3=0.1,and β1,2,3=0.99,respectively.The sampling time Δtis selected as Δt=0.001 s.
4.2.Simulation results
For the identification of the system state-space model and payload mass parameter,the following two situations are considered:(1)different payload masses captured at the same working point,and(2)the same payload mass captured at different working points.These situations are discussed in the following sections.
4.2.1.Simulation example 1:capturing different payload masses at the same working point
The system working point is still selected as (θ1)0=60°,(θ2)0=45°,and (η11)0= (η21)0=0.Three different payload masses Δmare discussed as follows:(1)Case 1:Δm=20 kg;(2)Case 2:Δm=50 kg;and(3)Case 3:Δm=100 kg.The RPBSID algorithm is implemented to identify the system state-space model parameters by using the designed I-O signals as discussed in Section 4.1.

Fig.2 Designed input torque signals u1and u2.

Fig.3 Response signals of rotation angles δθiand modal displacements δηi1(for Δm=20 kg and SNR=40 dB).
Different sets of the system state-space model satisfy the same I-O relationship.Thus,to verify the accuracy of the identified model,the same test inputs are applied to the original state-space model{A(k),B(k),C(k)}and the identified modelwith the initial state condition x(0)=^x(0)=04×1,and the test response values and the corresponding absolute errors are shown in Figs.4 and 5,respectively.The results indicate that the estimated test responses of the state-space model are generally consistent with those of the original system.
When the system matrix Acis identified,the system frequency ωjcan also be solved easily.The identified manipulator vibration frequencies ω1and ω2at the working point in the capturing procedure are shown in Fig.6.It should be noted that Fig.6 only provides the frequency identification results of Case 1 since the situations for Cases 2 and 3 are essentially consistent with those in Case 1 and therefore not shown here.In Fig.6,the system frequencies evidently change intcap=3 s due to the capture of the object.The results in Fig.6 indicate that the system frequencies change with the payload mass,and the recursive algorithm can also effectively identify the manipulator frequency at the working point.

Fig.4 System test response results for the identified state-space model parameters using the RPBSID algorithm at the working point(for Δm=20 kg,excluding measurement noise).

Fig.5 Absolute errors of system test responses between the original and identified state-space model parameters using the RPBSID algorithm at the working point(for Δm=20 kg).
When the state-space model parameters are obtained using the RPBSID algorithm,the payload mass can be determined by using the proposed method in Section 3.3 In this simulation,in addition to the proposed algorithm,the recursive least squares method and the algebraic algorithm are also employed to identify the payload mass Δm.The classical algebraic algorithm is commonly used for a single-link manipulator.Therefore,a dynamics model that only includes the second link and the endpoint payload is established when we apply the algebraic algorithm to identify the payload mass parameter.Besides,the gravity condition which is used in the algebraic algorithm is also provided in the simulation because the payload mass parameter is invariable whether it is in the space or on ground conditions.The main procedures of the algebraic algorithm for a single-link flexible manipulator can be briefly summarized as20

Fig.6 Identification results of frequencies ω1and ω2using the RPBSID algorithm at the working point(for Δm=20 kg).

where Δm(k)and ν(k)are the payload mass and the viscous friction damping coefficient for each sampling timek,respectively,and the recursive form of matrices Aa(k)and Ba(k)can be computed as

where the initial values Aa(0)and Ba(0)are zero matrices,(k)= [L2βa(k)+gLξa(k)ηa(k)],andgis the gravity acceleration.The expressions of parameters βa(t),ξa(t),ηa(t),andqa(t)are given respectively as


Fig.7 Identification results of the mass parameter Δm for different payload masses.

Fig.8 Absolute errors of the mass parameter Δm for different payload masses.

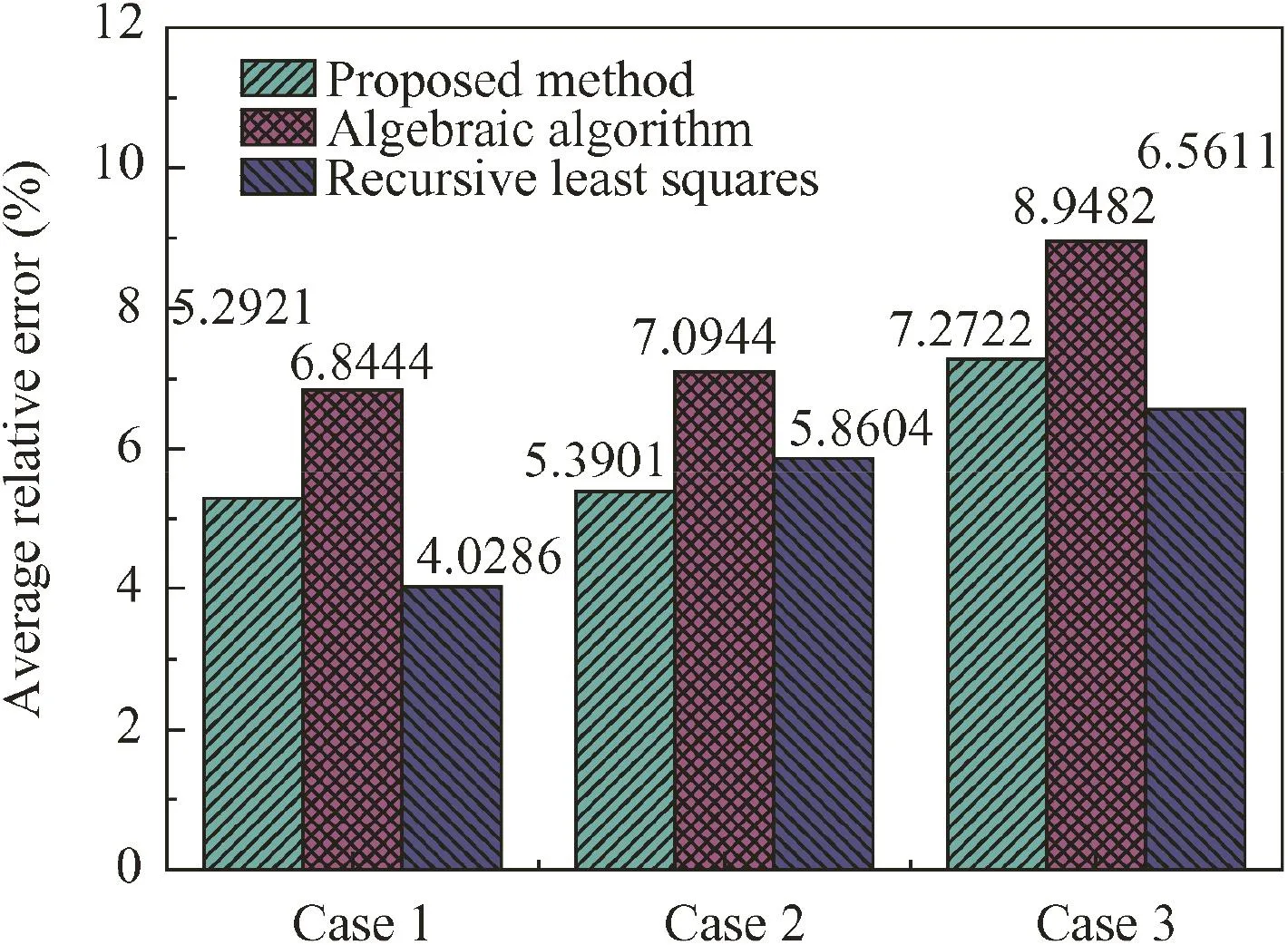
Fig.9 Average relative errors of the mass parameter for different payload masses using three methods(from 4 s to 6 s).
where Γ(t)and θt(t)are the computed angle of the tip position and the measured torque at the base of the link,respectively.Then,the functions βa(t),ξa(t),ηa(t),andqa(t)can be sampled at discrete timest=kΔt,k=1,2,3....The detailed procedures about the algorithm are provided in Refs.20,32 Now a total of 30 experiments are conducted for the three identification methods,and identified mass parameter results are shown in Fig.7.It should be noted that Fig.7 only displays the results from 4 s to 6 s because all the three algorithms require the iteration process to be as close to the original value between 3 s and 4 s as possible,and the identified results in the stable tracking phase using the recursive least squares method are slightly higher than the original values due to the flexible influence of the system.
Fig.8 shows the absolute errors of the identified payload mass parameter Δmwith time for the three methods,and the corresponding average relative errors are shown in Fig.9.The results in Figs.8 and 9 indicate that the proposed method can identify the payload mass parameter stably.Although the average relative error of the proposed method exhibits a certain increase with a change in the payload mass,the overall identification accuracy is still acceptable.
4.2.2.Simulation example 2:capturing the same payload mass at different working points(different configurations)
In example 2,the identification of the state-space model and payload mass parameter at different working points is implemented as follows:(1)Case 1: (θ1)0=0°and (θ2)0=0°;(2)Case 2: (θ1)0=45°and (θ2)0=0°;and (3)Case 3:(θ1)0=-45°and (θ2)0=45°.The corresponding three manipulator configurations are shown in Fig.10,and the payload mass is set as Δm=100 kg for each case.The other simulation parameters are the same as those in Section 4.1.

Fig.10 Three manipulator configurations.

Fig.11 System test response results of rotation angles δθ for three different configurations.
Test response results of rotation angles δθ for the identified state-space model are shown in Fig.11,and the corresponding absolute errors are shown in Fig.12.As shown in Figs.11 and 12,the results illustrate that state-space model parameters can be obtained by the RPBSID algorithm for different manipulator configurations.
Frequencies ω1and ω2for the three configurations using the RPBSID algorithm are shown in Fig.13,and Table 2 shows the average relative errors of the identified frequencies.The results indicate that the average relative error is less than 5%,which is acceptable for identification accuracy.

Fig.12 Absolute errors of system test responses between the original and identified state-space models using the recursive algorithm for three different configurations.

Fig.13 Identification results of frequencies ω1and ω2for three different configurations.

Fig.14 Identification results of the payload mass parameter Δm=100 kg for three different configurations.
In a manner similar to that of example 1,when the statespace model parameters are obtained,the three approaches are implemented to identify the payload mass parameter Δm.Fig.14 shows identification results between 4 s and 6 s for the three configurations,and absolute errors with time and the corresponding average relative errors are shown in Figs.15 and 16,respectively.The results in Figs.14-16 indicate that the proposed method can achieve a fast tracking speed to approach original values and exhibit satisfactory identification accuracy.
4.3.Finite element verification for the payload mass parameter
To further verify the validity of the presented method,in this section,a simple finite element model of a two-link manipulator is established,and the proposed recursive method is used to identify the payload mass parameter using the response data of the finite element model.The defined coordinate system is shown in Fig.1,and the working point is selected as(θ1)0=45°, (θ2)0=0°,and (η11)0= (η21)0=0.The payload mass is given as Δm=20 kg,and the other simulation parameters are the same as those aforementioned.

Fig.15 Absolute errors of the mass parameter Δm=100 kg for three different configurations.

Fig.16 Average relative errors of the payload mass parameter Δm=100 kg for three different configurations using three methods(from 4 s to 6 s).
Using the designed input signals as shown in Fig.2,an explicit dynamic analysis is carried out to generate system vibration response signals. Displacement and velocity responses about the middle position of theith link (i=1,2)are shown in Figs.17 and 18,respectively.In Figs.17 and 18,the displacement and velocity values of the 2nd link in the X-direction are almost zero because the corresponding vibration signals mainly reflect the link's lateral deflection.
Now by extracting the input and output data of the finite element model,the proposed method is used to identify the payload mass parameter again,and the identified mass parameter result from 4 s to 6 s is shown in Fig.19.It can be seen that now the identified error is higher than that of the theoretical computation in the paper because the finite element model is more sophisticated than the mathematical model,but at least the payload mass parameter can still be tracked after multiple iterations.

Fig.17 Displacement responses in the middle position of the ith link (i=1,2).
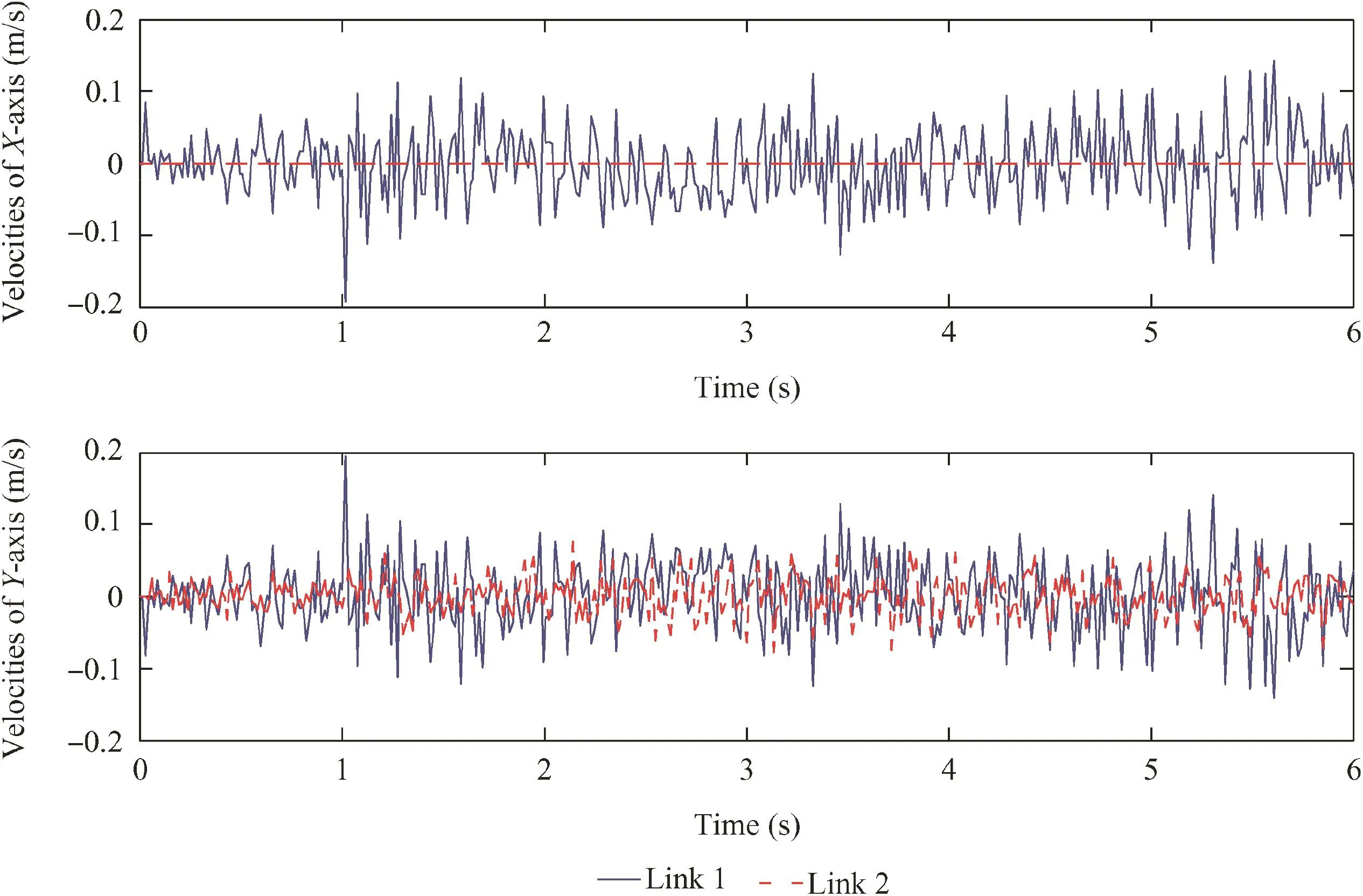
Fig.18 Velocity responses in the middle position of the ith link (i=1,2).

Fig.19 Identification results of the payload mass parameter Δm=20 kg using the proposed method for the configuration(θ1)0=45° and (θ2)0=0°.
5.Conclusions
(1)In this study,the state-space model identification of a flexible space manipulator is studied,and a novel method based on the recursive subspace algorithm is presented to estimate the payload mass parameter.By linearizing and reconstructing the manipulator nonlinear dynamics equation at a selected working point,system state-space model parameters are determined recursively using the RPBSID algorithm.
(2)Moreover,using similarity transformation of matrices,the payload mass parameter can be calculated by extracting the corresponding block matrix of the identified state-space model.In simulations,cases with different payload masses and working points are discussed.Computation results demonstrate that the proposed algorithm can be used to identify the manipulator state-space model and payload mass parameter for capturing an unknown space object.
(3)However,certain problems still exist and need to be improved in the proposed payload mass identification method,which include the following:(a)some prior knowledge,such as the values of matrices C,~M,Mc,and Ma-before,must be obtained before the identification,and the dynamics model of the space manipulator is established as a simply supported beam to simplify the derivation;and(b)the proposed method is based on the linearized model only at a certain working point,that is,it should satisfy the same working point before and after the capturing process.Hence,it is necessary to develop a more commonly used identification algorithm.
(4)From identification results of the system frequency in numerical simulations,it can be found that the modal parameters of the manipulator change at a fixed working point due to the variation in the endpoint payload mass.Therefore,a future study will attempt to establish the relationship between the system frequency and the payload mass and use the frequency difference value to estimate the mass parameter.For example,some online estimator methods used for flexible structures have been proposed to estimate frequency values and corresponding vibration signal parameters.34In this manner,the payload mass parameter can be determined simultaneously when the modal parameter identification procedure is implemented.
Acknowledgements
This work was funded by the National Natural Science Foundation of China(Nos.11572069 and 51775541)and the China Postdoctoral Science Foundation(No.2016M601354).
Appendix A
The detailed elements of matrices M(q)4×4,E(q,˙q)4×1,and K4×4in Eq.(7).
The detailed elements of the mass matrix M(q)4×4,the coupling coefficient matrix E(q,˙q)4×1,and the stiffness matrix K4×4in the nonlinear dynamics Eq.(7)before capturing a payload are expressed as follows,and the other unspecified elements in the matrices are all zero.

杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Guide for Authors
- Special Issue call for papers: Emerging Technologies of Unmanned Aerial Vehicles
- Effects of splined shaft bending rigidity on cylinder tilt behaviour for high-speed electrohydrostatic actuator pumps
- Efficiency optimized fuel supply strategy of aircraft engine based on air-fuel ratio control
- Event-triggered adaptive control for attitude tracking of spacecraft
- Reliable flight performance assessment of multirotor based on interacting multiple model particle filter and health degree
