A model-based prognostics method for fatigue crack growth in fuselage panels

Yiwei WANG,Christian GOGU,Nicolas BINAUD,Christian BES,Jian FU

aSchool of Mechanical Engineering and Automation,Beihang University,Beijing 100083,China

bInstitut Cle´ment Ader(UMR CNRS 5312)INSA/UPS/ISAE/Mines Albi,Universite´de Toulouse,Toulouse 31400,France

Abstract This paper proposes a model-based prognostics method that couples the Extended Kalman Filter(EKF)and a new developed linearization method.The proposed prognostics method is developed in the context of fatigue crack propagation in fuselage panels where the model parameters are unknown and the crack propagation is affected by different types of uncertainties.The coupled method is composed of two steps.The first step employs EKF to estimate the unknown model parameters and the current damage state.In the second step,the proposed efficient linearization method is applied to compute analytically the statistical distribution of the damage evolution path in some future time.A numerical case study is implemented to evaluate the performance of the proposed method.The results show that the coupled EKF-linearization method provides satisfactory results:the EKF algorithm well identifies the model parameters,and the linearization method gives comparable prediction results to Monte Carlo(MC)method while leading to very significant computational cost saving.The proposed prognostics method for fatigue crack growth can be used for developing predictive maintenance strategy for an aircraft fleet,in which case,the computational cost saving is significantly meaningful.

KEYWORDS Aircraft fuselage panels;Extended Kalman filter;Fatigue crack propagation;Linearization method;Model-based prognostics

1.Introduction

During aircraft take-off and landing,repeated pressurization/depressurization cause many loading and unloading cycles,which may lead to fatigue crack in the fuselage panels.1Several aircraft accidents due to catastrophic structure failure caused by fatigue cracks occurred in the previous century.2Prognostics focusing on the estimation of the future damage evolution and potential risk associated to a fuselage panel is crucial to aircraft safety.One of the most important functions of prognostics is to predict the Remaining Useful Life(RUL).3-6

From the theoretical point of view,damage prognostics can be regarded as the problem of time series analysis and forecasting.Time series analysis has two basic objectives:(A)to obtain the structure and underlying pattern of the observed data,and(B)to predict the future using previously observed data.Datadriven techniques are commonly used for time series analysis.These techniques are free from physical models relating to the failure or degradation mechanism.Instead,they rely on past recorded data to characterize the degradation process and to predict the future damage behavior.Two basic data-driven strategies involve:(A)modeling cumulative damage and then extrapolating out to predict the future damage,and(B)learning directly from data.The first strategy involves traditional techniques such as curve fitting,regression-based method,7,8Gaussian process regression,9Auto-Regressive and Moving Average(ARMA)model,10,11Autoregressive Integrated Moving Average(ARIMA)model,12,13etc.The second strategy mainly refers to various machine learning techniques that gain an increasing interest since the last decades such as neural network,14,15support vectors machine,16,17fuzzy time series,18,19etc.Deb et al.20gives a good review of data-driven techniques regarding both the above two strategies for time series analysis.

Data-driven techniques are appropriate in the cases when the understanding of the principle of system degradation is not comprehensive or when the system is sufficiently complex and thus developing an accurate degradation model is prohibitively expensive.However,implementing data-driven strategies has difficulties.Obtaining the run-to-fail data in particular for new systems can be lengthy and rather costly.When the future working condition of the system is not the same as that in the past,collecting data that include all possible future working conditions is impractical.In addition,the efficacy of data-driven methods depends not only on the quantity of the data but more on the quality of the data.If the data availability is not satisfied or the data is biased,the prognostics results can be imprecise or even incorrect entirely.21In contrast,model-based techniques can provide better performance than data-driven techniques if the degradation model of the system is available.22

In the application of fatigue crack growth in fuselage panels,the fatigue damage models have been well researched.23,24In this case,it would be more desirable to integrate the damage model into the prognosis in order to have an accurate and long-term forecasting,which is the idea of model-based prognostics.The crack growth can be modeled in myriad ways depending on whether the critical site is subjected to Multiple-Site Damage(MSD),Widespread Fatigue Damage(WFD),two-bay crack or other types of fatigue damage.Based on a study conducted by Molent and Barter,25in which the author reviewed fatigue crack growth data from a significant number of Full-Scale Fatigue Tests(FSFTs)on several different military aircraft types.Full-Scale Fatigue Test,the airframe was subjected to loads of varying amplitude and complexity for a specified period of testing.As the result of the review,Molent et al.concluded that a simple crack growth model adequately represents a typical crack growth.Here the well-known Paris' law is employed since it is widely used as the fatigue crack growth model.26,27The two parameters in Paris' law,mandC,are constants that depend on materials.25,28They are the so-called extrinsic material properties,which depends on loading and boundary conditions.Given the assumption that the loading has constant amplitude and boundary conditions are infinite,it is reasonable to assume thatmandCare constant.To our best knowledge,this assumption is consistent with other publications.29,30For a specific fuselage panel with specific material,the material parameters themselves are not random in nature but constants(Note that,throughout this paper,we use ‘Paris' law parameter”, ‘model parameter” and ‘material parameters” interchangeably to refer tomandC).However,due to lack of information,our knowledge on the true value of parameters is uncertain,and we use some probabilistic distributions to represent this uncertainty.In such cases,the probabilistic representation for model parameters does not mean that the parameters are random in nature so that it can be different values every time when they are realized.Instead,the parameters have true deterministic values,but their values are ‘unknown”.The distributions actually represent our knowledge level on the unknown parameters.For example,if the parameter distribution is wide,it means that our knowledge on this parameter is poor.This type of uncertainty is referred to as epistemic uncertainty and can be reduced by improving our knowledge through measurements that are related to parameters(since the parameters themselves cannot be measured directly).Taking the current application as an example,we measure the crack size,which is a function of model parameters,and infer the values of parameters through the measurements of crack size.This process is known as state parameter estimation using measurement data and is an important part of model-based prognostics.

If the damage model is accurate enough,it completes the prognosis since the future behavior of damage can be determined by propagating the damage model to future time.31In practice,however,the crack growth process is affected by uncertainties,e.g.,the epistemic uncertainty in the model parameters,the process noise,the measurement noise,etc.The key issue is to incorporate the uncertainties to get an accurate and reliable prediction to future.We model the crack growth process by using a state-space model or Hidden Markov Model(HMM),which is another branch of time series analysis and forecasting way besides the data-driven techniques32and has been used in prognostics in different applications.33,34Note that HMM can be seen as a specific kind of state space model,in which the states exhibit the Markov property.HMM applies in the cases where the state evolution of the system is hidden but can be revealed through observations.HMM contains two stochastic processes,a hidden Markov chain which represents the unobserved ‘actual state”,and an observable process that is the observed information collected over time shift.The nature of HMM matches well the modelling demand of the present application case,in which the actual crack growth is hidden but can be observed through measurement data perturbed by random noise.After modeling the crack growth process in a HMM framework,the model based prognostics method developed in this work is composed of two sequential phases:(A)estimating the fatigue crack size and unknown model parameters,and(B)predicting the crack size distribution in future evolution.

The first phase resorts to estimation algorithms based on noisy measurement data and typically handled by filtering techniques.35-37Here the Extended Kalman Filter(EKF)is chosen to address the state-parameter estimation problem.EKF has been used in prognostics area in many applications in the past three years.For example,Singleton et al.38employed EKF to the prognostics of bearings.The features were firstly extracted from the vibration signals and the curve fitting method was used to approximate the evolution of degradation.The fitted curve was used as the degradation model instead of using a physical model.Then the EKF was employed to predict the RUL of bearings.However,the distribution of RUL was not provided.Bressel et al.39applied the EKF to the prognostics of proton exchange membrane fuel cell,in which the RUL was computed each time a new estimate of the State of Health(SoH)being available by extrapolating the SoH to a threshold.Same as Ref.38,the distribution of the RUL was not provided.Xu and Chen40proposed a coupled Expectation Maximization(EM)and EKF method to perform the lithium-ion battery prognostics,in which the EM and the EKF algorithms were used to estimate the multidimensional parameters of the state-space model and the hidden state respectively.The probability mass function of RUL of lithium-ion battery was estimated by extrapolating the samples sampled from the joint state-parameter distribution after EKF estimation.Baptista et al.41combined data-driven prognostics methods with Kalman filtering to predict the RUL of aircraft bleed valve.The Kalman filter was used as an optimization module after the training and prediction stage of the data-driven methods to filter the RUL estimation.The case study results showed that the data-driven approaches with Kalman filter provide better prediction accuracy.From the above survey,it can be seen that EKF has been widely used in various applications.But few literature mentions fatigue damage prognostics on airframe structures using EKF.In our previous study,the theoretical applicability of EKF in the case of fatigue crack growth has been studied,in which EKF is compared with another variant of Kalman filter,the Unscented Kalman Filter(UKF),in various scenarios including minor nonlinear and strong nonlinear case,Gaussian measurement noise and uniformly distributed measurement noise.37The results show that EKF performs well in all cases with a quick convergence of state-parameter to their true values.In addition,EKF has comparable accuracy to UKF while leading to a considerable computational cost saving in practical application.

At the second phase of the model-based prognostics,once the joint state-parameter distribution is estimated,the straightforward method for predicting crack size distribution is Monte Carlo (MC)simulation,i.e.,sampling from the state parameter joint distribution and extrapolating each sample in the future time.However,MC simulation is time consuming.This might not be a disadvantage when dealing with one crack growth prediction in one fuselage panel.But in the case of a fleet in an airline including hundreds of aircraft with each one being composed of hundreds of fuselage panels,the computational cost by MC simulation can be prohibitively expensive.To address this problem,we proposed the efficient linearization method.Each time a new joint state-parameter distribution is estimated by EKF,linearization method computes analytically the trajectory of the crack size distribution hereafter.Different from other work of predicting the future state by extrapolating samples sampled from the joint stateparameter distribution after EKF estimation,the proposed linearization method is able to propagate the uncertainty analytically and give the trajectory of crack size distribution at any cycle beyond the last measurement.This is the first novelty of the proposed EKF-linearization method.Because of this analytical solution,the computational cost of linearization method is significantly reduced.Based on our experience,for doing prognostics(specifically,predicting the crack size distribution at next scheduled maintenance)for a fleet including 100 aircraft with each one being composed of 500 panels,the computational cost reduced from several days by using MC method to several hours by using the proposed EKF-linearization method.The second novelty lies in the fact that different from most work that predicts the RUL of a system,we predict the trajectory of crack size distribution for a given time interval.This is more desirable in the application of fatigue crack prognostics in fuselage panels since a fault or failure of a fuselage panel is catastrophic.Inspection and maintenance should be done regularly to avoid such failures.Therefore,it would be more desirable to predict the probability that a fuselage panel works normally before some future time,e.g.,next maintenance interval.The motivation of proposing the EKF-linearization method to efficiently compute the crack size distribution in future time is further detailed as follows.

The development of EKF-linearization method for fatigue damage prognostics is part of predictive maintenance strategy study for aircraft maintenance.Currently,the airlines perform the aircraft maintenance according to a fixed schedule,known as scheduled maintenance,during which the aircraft is sent to the hangar to undergo a series of time-consuming inspections.Recently,more advanced predictive maintenance strategies are gradually considered by aviation industry.It involves the usage of Structural Health Monitoring(SHM)systems that monitor the aircraft health state as frequently as needed.The data collected by SHM systems are processed by prognostics methods to predict the future health state,due to which,it is possible to plan the aircraft maintenance according to the predicted health condition rather than a fixed schedule.However,on the other hand,arbitrarily triggering maintenance purely based on the predicted health condition without taking into the scheduled maintenance might be disruptive to the traditional scheduled maintenance procedures due to less notification in advance.Therefore,it would be beneficial that scheduled maintenance works in tandem with SHM-based maintenance,more specifically,skipping some scheduled maintenance while maintaining aircraft safety through checking the aircraft health states more frequently by SHM system.In this situation,it is desirable to predict the crack size distribution at next scheduled maintenance.This prognostics information can be incorporated into the predictive maintenance to help decision-making.This is our motivation of predicting the crack size distribution in future time rather than RUL.

The main contribution of this work consists in proposing a computational efficient model-based prognostics method in the application of fatigue crack growth while considering different types of uncertainties including the unknown model parameters,the noisy measurement,etc.The remainder parts of the paper are organized as follows.Section 2 illustrates the problem statement.Section 3 details the state-parameter estimation using EKF.Section 4 proposes the linearization method,which allows predicting analytically the statistical distribution of the crack size in future flight cycles.In Section 5,a case study using the EKF-linearization method and MC method is implemented.Comparison in terms of prediction is done between these two approaches.In Section 6,we draw conclusions and suggest potential future work.

2.Problem statement

2.1.Degradation model

Fatigue damage in this paper means the existing flaws or cracks on the fuselage panels.In this work,the Paris'law is selected as the crack growth model,which is given by

whereais the half-crack size(m),kthe number of flight cycles,da/dkthe crack growth rate(m/cycle),mandCthe Paris'law parameters associated with material properties,ΔKthe range of stress intensity factor given as

whereAcis a correction factor intended to compensate for modeling the fuselage as a hollow cylinder,pthe pressure differential,rthe fuselage radius andtthe panel thickness.

Eq.(1)can be rewritten in a discrete form by applying Euler method,asak=ak-Δk+C（ΔK）mΔk.The precision of discretization depends on the discrete step.To reduce the discrete error,we set Δkto be one,i.e.,the discretization step of the Paris'law is taken at every flight cyclek,which is the minimal possible value from physical and practical point of view.Then Eq.(1)is written in the following recursive form at each flight cyclek.

It should be noted that by integrating the differential equation of Eq.(1)and solving fora,the crack size can be written analytically as a function of initial crack size,model parameters and number of cycles.The analytical expression of crack size afterkcycles is given in Eq.(4).Eqs.(3)and(4)should be asymptotically equivalent but might be different in numerical implementation.We compared the relative error of the crack size calculated by Eqs.(3)and(4).We found the relative error being smaller than 1%,which implies that the Paris'law with the discrete step size of one maintains a satisfactory accuracy in the application of fatigue crack growth.

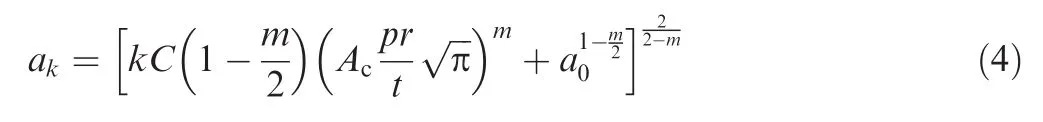
As explained in the previous section,model parametersmandCcontain epistemic uncertainty,meaning that they are true deterministic values and time invariant.But due to lack of knowledge,their true values are unknown and need to be estimated from measurement data on crack size.The pressure differentialpcan vary at every flight cycle.Then at each cycle,the pressure is a random variable expressed as

The disturbance Δpkis modeled as a normal random variable with zero mean and variance.Since the variation on the pressurepis generally small,the first-order Taylor expression is used to expand Eq.(3)with respect to the pressureparound its mean valueThis gives

2.2.Measurement model

With the advanced on-line condition monitoring technologies,such as the emerging SHM system,on-line monitoring data related to the unobservable crack size becomes available.Due to the harsh measurement environment and sensor limitations,the SHM data is often quite noisy.The measurement data is modeled by Eq.(10),in whichakis the true crack size,vkthe Gaussian measurement noise with mean zero and varianceRsuch thatvk~N(0,R).The Gaussian measurement noise is widely used in research works to simulate a realistic signal40,42since it is a good assumption for the process or system that is subject to the central limit theorem.43In the absence of information indicating otherwise Gaussian noise is often used to model measurement noise under the assumption of numerous sources of uncertainty and the central limit theorem.In our previous work,in order to assess whether EKF maintains its advantages when using the measurements with the other type of noise,we conducted additional studies.37A uniformly distributed measurement noise was tested.We found that the convergence of the state and parameters to their true values was satisfactory.Therefore,we consider that for the current application,EKF is relatively robust to the other type of measurement noise.

3.State-parameter estimation using past measurement data by EKF

In terms of state-parameter estimation,EKF is typically implemented through joint filtering,which defines the parameter vector of interest as an additional state variable and artificially appends it onto the true state vector.44Then the state and the parameters are estimated simultaneously.Readers may refer to our previous work for the detailed usage of EKF in the application of fatigue crack growth.37Here the estimation framework and work mechanism of EKF are briefly introduced for sake of the completeness.

3.1.Estimation framework

The two Paris'law parameters,mandC,are the parameters of interest that need to be identified from past measurement data.A two-dimensional parameter vector is thus built up as

The augmented state vector is obtained as

Note that the subscript ‘au” stands for augmented variables.Due to the extending of the state vector,the system transition function is accordingly extended,as represented in Eq.(13),and is expanded in matrix form for clarity,as given in Eq.(14).

Since the augmented state vector contains three elements,the variance of process noise should be accordingly extended to a 3-by-3 diagonal matrix,with the variance of process noise of each state variable as the diagonal elements.The covariance matrix of augmented process noise at time stepkis denoted by Qau,kand is given in Eq.(15),in whichQkis the variance of process noise on crack size in Eq.(9).

3.2.State-parameter estimation using EKF

The work mechanism of EKF is briefly introduced.We use ‘^”to represent an estimate and subscript ‘k” to denote the time step.The superscripts ‘-” and ‘+” indicate the prior estimate and the posterior estimate respectively.For example,represents the priori estimate of the augmented state vector at time stepkwhiledenotes the posterior one at time stepk.For the augmented system of Eq.(13),at each time step,the EKF is composed of two steps,prediction and update.

(1)Prediction

The recurrence formula of augmented system propagation is given in Eq.(16)and is rewritten in matrix form by Eq.(17)for the sake of clarity.

The covariance matrix P propagates as

where Φk-1is the Jacobian matrix of the augmented system equation at the point

(2)Update

The Kalman gain Kkis computed from

whereRis the measurement noise variance and Hkis the Jacobian matrix of the measurement equation at point

The estimated measurement is calculated by

The posterior estimate of state is updated through Eq.(23).For clarity,the matrix form is given in Eq.(24).

Finally,the covariance matrix is updated through Eq.(25),in which Iuis unit matrix.

4.Prediction approaches

The model-based prognostics that we discussed in this paper contains two sequential phases:(A)estimating the crack size and the unknown Paris'law parameters up to the present time(denoted byS)using a sequence of measurement data collected during the aircraft service life untilS,and(B)based on the estimated states at timeS,predicting the statistical distribution evolution of the crack size in the futureIflight cycles.It is more desirable to predict the probability that a panel will operate normally before some future time than to predict its RUL.The first phase has been addressed in Section 3 while the second one requires going beyond the use of filtering methods since it involves future time horizons in which no measurement is available.In this section,we make efforts to address the prediction problems in the second phase by applying MC method and the newly proposed linearization method.At the end of the first phase(timeS),the following information is considered available from EKF and will be used as initial conditions of the second phase for both the MC method and the linearization method:(A)expected value of the augmented state vector,

4.1.MC method for prediction

The symbol ‘MC” in the superscript stands for ‘Monte Carlo”method in order to distinguish the linearization method that will be discussed in Section 4.2.The schematic diagram of predicting crack size using MC method that is discussed above is illustrated in Fig.1.

4.2.Linearization based method for prediction

The objective of the linearization method is the same as the MC method,which aims at predicting more efficiently the evolution of the crack size distribution fromS+1 toS+I.Let us define

Fig.1 Schematic diagram of predicting crack size using Monte Carlo(MC)method.

Note that the indexkstarts fromS+1 and propagates untilS+I,i.e.,k=S+1,S+2,...,S+I.The concept of ‘expected trajectory” is first introduced since it is related to the derivation of linearization method.A trajectory is a particular solution for a stochastic system with a particular realization for each random variable involved.45The term‘expected trajectory” in this case is referred to as the trajectory that is obtained when the random variables are taken their expected values.We use the hat symbol ‘-” to denote the expected value of a random variable,e.g.,represents the expected value ofak.For the problem discussed at hand,the‘expected trajectory” of the crack size is the sequence=S+1，S+2，...，S+I｝ obtained as a solution of the following equation with zero process noise and with the expected valueas the initial conditions.

Due to the presence of random noise,akandpkare considered random.mandCcontain the epistemic uncertainties.The uncertainties in the above four variables are modeled through adding a perturbation around their expected values.Let the symbol‘Δ” denote the perturbation from the expected values,and then the realak,m,Candpkare modeled as

Δpkis related to the cabin pressure differential that varies from one flight cycle to another.The available information given by EKF atk=Swill be used as the initial condition in the following derivation:

Subtracting Eq.(31)from Eq.(30),the perturbation ofakis represented as

Eq.(45)provides a way to calculate the perturbation of crack size at any cycle.Note that[ΔaS,Δm,ΔC]Tis multivariate normally distributed with mean zero and known covariance(recalling Eq.(37)),and then the distribution of Δakcan be analytically calculated.The following equations give the three-step forward derivation as examples and afterktimes iteration the analytical formula for calculating Δakis given in Eq.(46).For simplicity,we useAk,BkandDkto represent the coefficient of Δas,Δmand ΔCrespectively at time stepkwhileEkdenotes the noise term.

Note that in Eq.(46),ΔaS,Δmand ΔCare stationary random variables whose statistical distributions are time invariant.Ak,BkandDkevolve with time and can be calculated recursively with their initial valuesLS,MSandNS,as given in Eqs.(47)-(49).Ekis the only random variable with distribution varying from cycle to cycle and is derived recursively by Eq.(50).Given thatEkis a linear combination of independent and identically normally distributed variables(k=S,S+1,S+2,...),it is thus a normal variable such thatEk~N(0,Fk),in whichFkrepresents the variance ofEk.Using the recurrence of Eq.(51),Fkcan be obtained recursively with its initial value σS.Note thatand σkin Eqs.(50)and(51)refer to Eqs.(43)and(44)respectively.

The above formulas allow to compute analytically the evolution of the crack size distribution from cycleS+1 to cycleS+I.As a summary,the process of calculating the mean and standard deviation of crack size at thek-th flight cycle is reported in Table 1.

5.Case study

In this section,we investigate the performance of the proposed EKF-linearization approach.We first describe the test case involving fatigue growth on a fleet of aircraft.Then,we present the results concerning the Paris'law parameter estimations using EKF.Finally,we provide prediction comparison between the linearization and the MC method.

Table 1 Linearization-based procedure summary.

5.1.Settings of case study

The parameters involved in the numerical application are classified into three categories:(A)parameters related to panel-topanel variability;(B)parameters related to EKF algorithm;and(C)aircraft geometry parameters.

A fuselage is composed of several hundred panels.If all the manufactured panels are exactly the same and these panels work in exactly the same conditions and environment,the panels will degrade totally identically.However,in practice,due to intrinsic variability in fatigue propagation,the difference of material quality and the various working environment,etc.,uncertainties are considered in the degradation process.For example,each panel can have its own initial crack size,material properties and loading condition.We refer to such uncertainties related to variation between individual panels as panelto-panel uncertainty.In this study,aN,mN,andCNare used to denote the panel-to-panel uncertainty of the initial crack size and Paris'law parameters of the population of the fuselage panels.Note thataN,mN,andCNare random variables and we useto stand for the realizations.The panel-to-panel uncertainty is modeled by assuming thataN,mN,andCNfollow some predefined statistical distributions.Specifically,aNis assumed logarithmic normally distributed whilemNand lgCNare assumed to follow a multivariate normal distribution with a correlation coefficient of-0.8,based on the research indicating thatmand lgCare negatively linearly correlated.46-48

For each individual panel,we drawfrom the above-mentioned distributions to represent the panel-to panel uncertainty discussed in the above paragraph.These drawn values are regarded as the unobserved ‘true”values that need to be estimated by the EKF from measurements.The noisy measurements are simulated by adding Gaussian white noise to the ‘true” crack size value.This data is used as the actual measurements for the estimation process.During the EKF estimation process,only these noisy measurement data are available,from which the crack size and the material property parameters should be estimated.Besides the measurement uncertainty,we also take into account the load uncertainty,i.e.,the pressure differential,which varies at every flight cycles and is modeled as a normal variable.The EKF algorithm needs to be initialized.In particular,the starting point of the estimation algorithm has to be provided.In our case,the starting point is drawn randomly from uniform distribution centered at the ‘true” valuerespectively and having a range of 50%around these true values.Once this initial guess has been provided,EKF makes estimation of^ak,^mk,and^Ckat each cyclek.Note that,to avoid a systematic bias,the starting point of the EKF algorithm is different(draw randomly)for each panel in the aircraft.As for the initial error covariance matrix P0,it is chosen depending on how much confidence one has to the initial estimates.

Our potential application object is a typical short-range commercial aircraft with a typical lifetime of 60000 flight cycles.The values of the time invariant geometry parameters defining the fuselage(e.g.fuselage radius and panel thickness)are related to such aircraft.For recall,we define a correction factorAc,which intends to account for the fact that the fuselage is modeled as a hollow cylinder(without stringer and stiffness).A numerical value has been chosen from the studies by Pattabhiraman et al.49All the values of the above mentioned three types of parameters are reported in Table 2.

To take into account the panel-to-panel uncertainty,we assumeNp=100 fuselage panels.aN,mN,andCNare drawn from their respective distribution given in Table 2 and assigned to each panel,i.e.to form the initial condition of thej-th panel.For thej-th panel(j=1,2,...,Np),the numerical experiment is implemented as follows.

Table 2 Parameters used in numerical study.

The cracks in the ‘critical panels” have high crack growth rate and will exceed the threshold before the end of life of the aircraft,indicating that the crack growth curves show a strong nonlinearity.In contrast,the ‘non-critical panels”means that the cracks maintain a moderate or very low growth rate and thus the crack growth curves show a‘minor nonlinearity” during the whole lifetime of the aircraft.Our previous work shows that EKF has good performance in both minor and strong nonlinear cases.37This allows us to have high belief that if the EKF-linearization method performs well in the strong nonlinear crack growth process(corresponding to the critical panels),it reasonably maintains good efficacy for the minor nonlinear cases(corresponding to non-critical panels).Nevertheless,in order to confirm this behavior,we test additional non-critical panels besides the critical ones.Note that the service lives of the non-critical panels are longer than the lifetime of the aircraft(60000 cycles).We predict the crack growth trajectories in the lastJcycles up to the end of life of the aircraft as well as up to the service life of each non-critical panel in order to give more evidence.

5.2.Results

There are eight ‘critical panels” out of the population of 100,meaning that the cracks in these eight panels will exceed the threshold before the end of life of the aircraft.We then select the ten panels that have the shortest service life from the remaining 92 non-critical panels to verify the proposed method(the service lives of 92 panels are sorted in ascending order and the first ten panels are picked).The initial condition and the service lives of the eight critical panels as well as the ten non-critical panels are listed in Table 3.

5.2.1.State-parameter estimation

In this part,we present and analyze the state-parameter estimation by EKF through reporting the results of panel No.7 as an example.Panel No.7 is representative since it has the shortest service life(33617 cycles)and is thus the most critical one among the critical panel panels.The crack size estimation is shown in Fig.2.Fig.2(a)is the comparison between true crack sizeakand the EKF estimatefrom the first cycle up to 4000 cycles before the end of service life of this panel,i.e.the 29617th cycle.Each point represents a noisy measurement used in the EKF.Note that only one point every 100 cycles is represented in order not to overload the figure.It can be seen that the estimated crack length(dashed line) fits well the true one(solid line).Fig.2(b)gives the relative error betweenaandwhich begins with a high value of 7%due to a large biased initial estimate for crack size and decreases rapidly to nearly 1%after 100 flight cycles.Then it fluctuates to a small extend but keeps very low(less than 2%)and overall declines progressively.

The parameter estimation results are shown in Fig.3,which indicates thatmandCconverge to their true values as time evolves.Fig.3 also gives the 95%Confidence Interval(CI)of the estimates,from which it can be observed that the spread decreases over time.

Table 3 Information of critical and non-critical panels.

Fig.2 Crack size estimation by EKF.

5.2.2.Crack size evolution prediction

In this part,we analyze the prediction results of the eight critical panels and the ten non-critical panels.Our aim is to compare the predicted distribution of crack size given by MC and linearization methods in the lastJ=4000 cycles before the end of the panel's service life.For the non-critical panels,their service lives are longer than the lifetime of the aircraft.In order to give additional evidence,for each non-critical panel,we predict the distribution of the crack size up to the end of life of the aircraft(60000 flight cycles)as well as up to its service life(Note that the service life is presented in Table 3).According to the nature of the EKF-linearization method,the crack size is normally distributed,which is characterized by mean and standard deviation.Therefore,comparison of these two methods can be implemented through comparing the error betweeni.e.the mean and standard deviation given by MC and linearization methods respectively.The results of the maximal error in the lastJflight cycles are reported in Table 4.Note that the maximal error is obtained at the last cycle.The first column of Table 4 is the index of the critical and non-critical panels whose initial condition and the corresponding service life have been presented in Table 3.We see that,for the noncritical panels,the crack size at the end of life of the aircraft(the 60000th cycle)is far less than the thresholdath.According to the results,we draw the following comments.(A)Linearization-based method gives very close results to that of MC METHOD with maximal relative error 0.317%for mean and 1.84%for standard deviation.(B)For panels Nos.1,5,7,and 9,the mean of the crack size estimated by the linearization method is underestimated(i.e.smaller than the true crack size).However,when considering the 95%confidence interval,the prediction remains conservative.The same conclusion holds for the non-critical panels Nos.13,15,and 16 in the case of prediction up to their respective service life.For all other panels,the predicted means of the crack sizes are greater than the true ones.This conservative prediction leads to a right decision of repairing or replacing the panels thereby ensuring the safety of the aircraft.The last column presents all the 95%confidence interval of the predicted mean.(C)The linearization method shows its great advantage in computational cost over MC METHOD(5000 samples are used)with 0.144 s versus 889.254 s,on a desktop with a processor Intel(R)Core(TM)i3-4130 CPU 3.4 GHz.This computational saving is significantly meaningful when dealing with a fleet being composed of hundreds of aircraft in airlines.

Fig.3 Convergence process of m and C.

6.Conclusions

In this work,we proposed a model-based prognostics method that couples EKF and linearization approach for the application of fatigue damage propagation in fuselage panels.Both the material property parameters and the initial crack size are unknown and both the measurements of crack size and loading conditions are affected by uncertainties.The presented model-based prognostics method includes two sequential phases:(A)state-parameter identification from noisy measurement data using the EKF algorithm,and(B)future damage prediction using the proposed linearization method.The results show that the EKF performs well in state-parameter estimation process during which the crack size has been well estimated and the estimated mean values of the two unknown material property parameters converge to their true values over time.In the second phase,the proposed linearization method is employed to predict analytically the evolution of the crack size distribution in some future flight cycles from the present estimations given by the EKF.The results are compared to those of MC method.The comparison shows that the linearization method gives similar prediction performance to MC METHOD with a great saving in computational cost.Both MC and linearization methods provide right decisions of repairing or replacing panels.This indicates that the linearization method is effective and can be used to replace MC method in application of prognostics of fatigue crack growth.This is of particular significance when dealing with large number of aircraft,e.g.planning maintenance strategies for a fleet of aircraft,which is our future work.

Table 4 Comparison of mean and standard deviation of crack size given by MC and linearization methods at the last predicted flight cycle.

Acknowledgement

The present work was partially funded by the National Natural Science Foundation of China(No.51805262).