Impact of reduced frequency on the time lag in pressure distribution over a supercritical airfoil in a pitch-pause-return motion

Hghight Z.ESLAMI,Ali R.DAVARI,*,M.R.SOLTANI

aAerospace Division,Department of Engineering,Science and Research Branch,Islamic Azad University,Tehran 147789-3855,Iran

bDepartment of Aerospace Engineering,Sharif University of Technology,Tehran 147789-3855,Iran

Abstract Effects of reduced frequency,stop angle,and pause duration have been studied on a thin supercritical airfoil undergoing a pitch-pause-return motion,which is one of the classic maneuvers introduced by the AIAA Fluid Dynamics Technical Committee.Experiments were conducted in a low-speed wind tunnel at both a constant mean angle of attack and an oscillation amplitude with a reduced frequency ranging from 0.01 to 0.12.The desired stop angles of the airfoil were set to occur during the upstroke motion.The unsteady pressure distribution on the airfoil was measured for below,near,and beyond static stall conditions.Results showed that the reduced frequency and stop angle were the dominant contributors to the time lag in the flow field.For stop angles in both below and post-stall regions,the time for the flow field to reach its steady state conditions,known as the time lag,decreased as the reduced frequency was increased.However,in the static-stall region and for a certain value of reduced frequency,a resonance phenomenon was observed,and a minimum time lag was achieved.The pressure distribution in this condition was shown to be highly influenced by this phenomenon.

KEYWORDS Dynamic stall;Pitch pause return motion;Reduced frequency;Static stall;Time lag

1.Introduction

The continuing development of high-performance aircraft has put unsteady problems into forefront of aerodynamic investigations.Especially,research about oscillating airfoils has been a topic of study for decades.Because of the inherent complexities in such time-dependent problems,a great deal of both theoretical and experimental surveys have been performed to understand and explain the flow physics governing such motions.

These studies have mostly focused on pure pitching or plunging airfoils,and very limited data is available for other types of motions,one of which is the pitch-pause-return maneuver.This motion is usually considered in studies involving the aerodynamics of aggressive perching maneuvers.In such maneuvers,large lift and drag forces are produced due to a rapid increase in the angle of attack.The capability to sustain the lift at an angle of attack typically higher than the static stall angle is the key feature to a successful maneuver.

Herbst1introduced for the first time the pitch-pause-return motion.This type of maneuver encompasses a rapid pitch-up to 90°,maintaining this condition for 2-3 s followed by a fast return to the initial conditions.Intensive surveys have then been reported on NACA0012,NACA0015,and flat plates,mainly during a sinusoidal pitching motion.

Walker et al.2investigated the pitch motion on a NACA0015 airfoil in a subsonic wind tunnel.For low pitch rates,they observed a separation bubble a little after the motion is commenced,followed by formation and growth of the leading-edge vortex.They stated that the maximum lift is achieved when this vortex is matured and attached to the surface.

In another research reported by Visbal and Shang,3a numerical study was performed on a pitching airfoil up to a very high angle of attack.They observed a small separation bubble near the trailing edge at zero incidences.They found that when the pitching motion starts,this separation bubble moves to the upper surface towards the leading edge while the flow at the lower surface is completely attached.As a result,the counter-clockwise vortices which are continuously shed into the wake give rise to the total circulation around the airfoil.This,in turn,increases the lift.

Shih et al.4in an experimental survey investigated the unsteady flow pastaNACA0012 airfoil in a pitching-up motion in a water towing tank using the Particle Image Displacement Velocimetry(PIDV)technique.The airfoil pitching motion was from 0°to 30°angle of attack at a constant pitch rate.

They also noticed the role of the lower surface in generating small vortices which are accumulated to form the starting vortex.They found no evidence of the trailing-edge separation bubble for below-static stall angles.These bubbles are generated near static stall angles and grow up as the angle of attack is further increased.

A similar observation was reported by Akbari and Price5on NACA0012 during a pitching motion beyond the static stall angle which has been measured to be 15°.They found that the separation bubble around the leading edge appears at an angle of attack of about 17°and increases in both size and strength at higher angles.At an angle of about 22°,the bubble bursts and separates from the surface,which is the dynamic stall onset.The flow reattaches to the surface during downstroke.They also concluded that both separation and re-attachment start from the leading edge.

Ol et al.6,7followed the recommendation of the AIAA Fluid Dynamics Technical Committee(FDTC)at Low Reynolds Number Discussion Group(LRDG)and introduced the pitch-pause-return motion as a standard maneuver usually performed by Micro Air Vehicles(MAVs).

Baik et al.8studied the leading-and trailing-edge vortices dynamics on a rapidly pitched flat plate with smooth starting and stopping phases,using dye flow visualization and 2D PIV.They have shown that for low reduced frequencies,a strong Leading-Edge Vortex(LEV),and a relatively weak Trailing-Edge Vortex(TEV),exist in the flow field,while for high reduced frequencies,the TEV appears prior to the LEV.The formation of the LEV,in this case,is postponed until the plate is in the end phase of the motion.

Ramesh et al.9studied this pitch-pause-return motion for a flat plate,using theoretical computational and experimental approaches.They examined several locations for the pitch axis and compared the results obtained from different methods.They also investigated the effects of the pitch axis location and stop angles on the location of the leading-edge vortex,separation and vortex mechanisms at the beginning and end of the cessation of the motion.They observed that the leading-edge vortex formation is initiated at the upstroke,while the location of separation depends on the pitch axis and stop angle and differs between upstroke and downstroke motions.Detachment of the vortex is accompanied by reversal of flow on the surface of the airfoil and causes deep stall and a significant reduction in lift during the hold and downstroke phases.

Granlund and Ol10investigated the pitch-up motion of a flat plate in a water tunnel.Having injected dyes to the flow,they observed that the maximum lift depends on the maximum size of the leading-edge vortex just before shedding into wake.The maximum lift was also found to occur at higher angles of attack,as increasing the reduced frequency.

Teyu et al.11,12studied the pitch-pause-return motion of a flat plate in a water tunnel.They observed a strong dependency of lift to the stop angle.Just at the pause moment after pitchup,if the vortices are not matured,the lift continues its increasing trend during upstroke to further growth of the leading-edge vortex.According to their results,for a pause angle of 33°,the leading-edge vortex had not grown enough,and the lift at the pause duration was still increasing.For 45°and 75°stop angles,a fully developed leading-edge vortex was observed,and the lift at the stop time was seen to be decreased.

Supercritical airfoils, firstly introduced by Whitcomb,are efficient airfoils for transonic and supersonic flights,and have been widely used in modern commercial aircraft.The upper surface of these airfoils is relatively flat to postpone the formation of normal shock,and a highly cambered region is provided for the lower surface near the trailing edge to make up for the loss in lift due to the low curvature on the upper surface.13

This relatively modern configuration for airfoils has successfully reduced the wave drag and the fuel consumption,and become a popular configuration for high-speed flight since its appearance in 1960s.Even though valuable information has already been obtained about the aerodynamic characteristics of these airfoils in transonic and supersonic regimes,very limited studies have been devoted to the low-speed regime where an aircraft has to perform take-off,landing,and different maneuvers.The later gets even more complicated,since unsteady flow would be encountered.Recently,limited data has been published on SC-0410,which is a thin supercritical airfoil in transonic steady flow.14

In this paper,a supercritical airfoil has been tested in a lowspeed wind tunnel to study the aerodynamic behavior while the airfoil was performing a pitch-up and hold maneuver followed by a pitch-down motion to return to the initial condition.Instantaneous pressure distributions on both upper and lower surfaces have been measured during the maneuver.Results have revealed valuable information about the role of the stop angle while pitching up as well as the pause duration on the unsteady aerodynamic characteristics and the time lag in the flow field.

2.Unsteady flow field around an airfoil

For a symmetric airfoil,impulsively put to a positive angle of attack,Prandtl and Tietjens15has visualized the flow field in a water tunnel.He also described the formation and separation of the counterclockwise vortex at the trailing edge.Fig.1 shows the starting vortex at the trailing edge due to a sudden angle-of-attack change.This TEV can be explained by the flow processes occurring within the boundary layer.

At a zero angle of attack,the upper boundary layer contains a clockwise vorticity,while a counterclockwise vorticity exists within the lower boundary layer.At the trailing edge,the two boundary layers merge and resemble a wake structure.A sudden change in the angle of attack is accompanied with an increase in both clockwise and counterclockwise vorticities in the boundary layer.Nevertheless,the counterclockwise vorticity inside the lower boundary layer dominates the flow for a while and forms a distinct TEV which decays once the Kutta condition is satisfied.However,for impulsively started or periodic motions,the induced angle of attack changes with time,and the process to create and fade the TEV goes on.

For harmonic oscillating airfoils,both an LEV and a TEV exist.As the LEV passes over the Trailing Edge(TE),the shear layer on the lower surface rolls up from the TE to the upper surface,generating the TEV.

Fig.2 shows the vorticity field obtained from the PIV results,around an airfoil in a sinusoidal plunging motion.16In this case,the instantaneous induced angle of attack periodically changes,and the LEV and TEV are continuously generated and shed downstream.As shown in Fig.2,the LEV passes over the TE,and the TEV is formed at the TE.The parameter ωzc/u∞is vorticity,in which,ωzis the angular velocity andcis the cord length.

3.Experimental apparatus

Experiments were conducted in a subsonic wind tunnel of a close return type having test-section dimensions of 80 cm×80 cm×200 cm.The tunnel operates in a speed range from 10 to 100 m/s.The present experiments have been performed at a constant speed of 30 m/s corresponding to a Reynolds number of 0.45×106.This tunnel is equipped with four large anti-turbulence screens and a honeycomb in its settling chamber to reduce the tunnel turbulence to less than 0.1 percent in the test section.

The model used in the present experiments was a rectangular 2D wing with a supercritical airfoil section,SC-0410.The chord length was 30 cm,and the wing span was 80 cm.Two views from this model are shown in Fig.3.

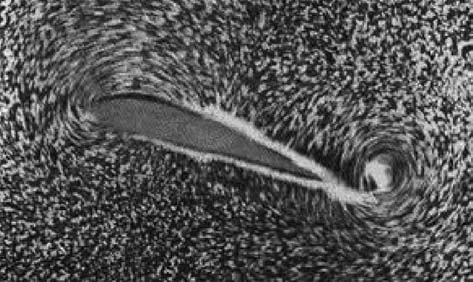
Fig.1 Visualization of a starting vortex due to a sudden angle of-attack change.15

Fig.2 Instantaneous vorticity field around a plunging airfoil.16

Fig.4 shows the schematic view of the wing section along with the pressure tap locations.35 pressure ports were carefully drilled on the upper surface and 50 on the lower surface.Due to the sharp trailing edge,no pressure ports could be provided between 0.95＜x/c＜1.0

Pressure data has been sensed by pressure transducers,and output signals were recorded,at a sample rate of 500 Hz,by two terminal A/D boards with 64 and 48 inputs,respectively.The raw noisy data was then imported to a PC and filtered digitally by a low-pass filtering routine to obtain clean and clear signals.

Single-sample precision and bias uncertainty in each measured variable were estimated and taken into account in the calculation process.The maximum uncertainty calculated in the present experiments was±%3.

Fig.3 Model manufactured for the present experiments.

Fig.4 Schematic view of the pressure taps on the model.

Fig.5 Motor and oscillation mechanism.

Fig.6 A typical scenario for the pitch-pause-return motion.

The oscillation system produces a pitching motion about the quarter chord axis according the equation α=7.05+15.65sin(2πft),where the mean angle of attack is 7.05°,the oscillation amplitude is 15.65°,andfis the frequency of motion.The reduced frequencies in these experiments were between 0.01 and 0.12.The pitch-pause-return motions of the airfoil were controlled by a pre-planned smart motor.Fig.5 shows the motor and the oscillation system used in these experiments.

The desired stop angles of the airfoil were selected during its upstroke phase.The mean angle of attack,oscillation amplitude,and pitch axis were considered constant in these experiments.The stop angles were 5°,10°,and 15°,which are below,around,and beyond the static stall angle of attack,respectively.The static stall angle of attack for this airfoil has been measured to be about 10°.

When the model was at a 0°angle of attack,the pitching motion has been commenced.The angle of attack then started to increase according to the aforementioned sinusoidal equation,until the desired stop angle was achieved,in which the motion was ceased for a pre-specified time.Thereafter,the angle of attack decreased to zero degree according to the same equation.Data acquisition continued until about two seconds after the end of this pitch-pause-return motion.

In a typical scenario,the model stopped at a 15°angle of attack for 0.5 s.The angle of attack variations for this case are shown in Fig.6,for different reduced frequenciesk.

4.Results

Fig.7 Surface pressure distribution on the airfoil in static cases.

Experiments were performed at both static and dynamic pitchpause-return conditions.Fig.7 shows the surface pressure coefficientCpdistribution on this airfoil for the static case at various angles of attack up to the post-stall range.The static stall angle of the SC-0410 airfoil is about 10°.

For angles of attack below the static stall,the pressure distributions are nearly identical on the lower surface near the trailing edge,as shown in Fig.7(a).This region has a relatively high curvature,which is common in supercritical airfoils.

For angles of attack below 8°,the suction peak moves forward towards the leading edge as increasing the angle of attack.However,this point moves aft for angles from 9°to 11°.At α =12°,the suction peak is seen to disappear,as shown in Fig.7(b).Furthermore,beyond the stall angles of attack,as shown in Fig.7(b),the pressure distributions are observed to be unchanged on the lower surface near the leading edge.To check the data accuracy,some numerical simulations have also been performed in some static cases.Fig.8 compares the lift coefficientsCLobtained by the CFD simulations with those calculated form integrating the experimentally determined pressure over the surface.Despite a small overestimation,good agreement can be observed between the results within the angle-of-attack range examined for the CFD simulations.

Dynamic tests have been performed at three stop angles corresponding to below,near,and beyond the static stall regions.

Fig.8 Comparison of lift coefficients between CFD and experimental results for static cases.

4.1.Case 1(Below static stall)

In this case,the wing stops at a 5°angle of attack.The dynamic pressure distributions for a reduced frequency ofk=0.01 in four distinct phases of the pitch-pause-return motion are shown in Fig.9.The points a,b,c and d correspond to the start point of upstroke,the start point of pause,the start point of downstroke,and the end of downstroke,respectively.The pause duration was set to 0.3 s.

From Fig.9,it can be observed that the pressure distributions for all the four phases are nearly identical at the rear part of the lower surface.For small angles,the difference in pressure distribution between the upper and lower surfaces can be integrated to calculate the lift coefficient.The value of the lift coefficient in this case increases in upstroke and pause phases and decreases during downstroke.Due to time lag and phase difference,the flow behavior in upstroke motion is completely different from that during the downstroke portion of the motion.Consequently,the lift coefficient would exhibit a hysteresis behavior with an instantaneous angle of attack as shown in Fig.10.

The dynamic lift coefficient during upstroke is lower than the corresponding static value,but is higher than the static one in the downstroke motion.

Fig.9 Instantaneous pressure distributions in four phases of the motion for case1.

Fig.10 Hysteresis loop of the lift coefficient,k=0.01,pause duration=0.3 s.

During upstroke,the flow is attached to the surface.As the angle of attack increases in the pitching motion,the lower surface continuously sheds small-scale counter-clockwise vortices that roll up into the wake and form a starting vortex.This,in turn,increases the circulation around the wing and gives rise to the lift.The increasing trend of lift proceeds up to the stop angle,in which the flow is still attached to the surface,and the increase in lift continues at a steeper rate.

At the end of the stop phase,as the airfoil proceeds downstroke,the circulation around the wing and consequently the lift start to decrease.3,4The upstroke condition has an important role in the motion time history,and the flow phenomena during stop and downstroke phases strongly depend on it.Thus,the effect of reduced frequency on the pressure distribution at the end of the upstroke phase,i.e.,the beginning of pause,would be of great importance.This is shown in Fig.11,for two different reduced frequencies and 0.1 s pause time.

As can be seen,the pressure distributions for both reduced frequencies at the beginning of the pause phase,lay inside the corresponding static values.It is important to note that the pressure distribution in the cambered region on the lower surface near the trailing edge is observed to be nearly independent of the airfoil motion.The static pressure distribution in this region almost coincides with the dynamic one.Further,as increasing the reduced frequency,the area between the pressure distribution curves on the upper and lower surfaces,which is an indication of the lift coefficient,also decreases.At sufficiently high reduced frequencies,there would not be enough time for the flow field to follow the rapid motion of the airfoil.As a result,the lift remains more or less constant.

Fig.11 Effect of reduced frequency on the pressure distribution just at the moment of pause for case 1.

The time variations of the lift coefficient are shown in Fig.12 at a 5°stop angle,with a pause duration of 0.2 s.Here,the distance between two hollow markers indicates the pause phase.Once the downstroke motion is finished,the airfoil reaches back to the position before maneuver while experiencing a different flow field,due to the unsteady motion in its time history.This position is designated by a filled marker in Fig.12.

The maximum dynamic lift coefficient decreases as increasing the reduced frequency.This shows that the flow is attached on the surface during the upstroke phase.However,the leading-edge vortex appears on the upper surface and extends,while the airfoil proceeds its downstroke motion.5The increasing behavior of the lift coefficient during the pause phase emphasizes the decisive role of the motion time history during and prior to pause.

At the end of the downstroke motion,the airfoil reaches a 0°angle of attack,after which sampling goes on for another 2 s.The time needed for the flow to recover to its steady state value at a zero angle of attack is known as the time lag.During this interval,a rapid decrease can be observed in the value of the lift coefficient until it reaches its static value at α =0°.

The time lags in the flow field for various reduced frequencies are shown in Fig.13 for a pause duration of 0.1 s.For higher reduced frequencies,the time to reach the steady value,i.e.,the time lag,reduces.This is due to an increase in the energy dissipation as the reduced frequency increases.

According to the results,the time lag in the flow field is not affected by the pause duration as shown in Fig.14.

A typical pressure tap located atx/c=0.42 is considered to study the time lag behavior.At this specific position,the flow is always attached to the surface,and no evidence for flow separation has been found at this position during the pitch-pausereturn motion.

Shown in Fig.15 are the time variations of the pressure coefficient at this point for three different reduced frequencies.The time lag in this figure is measured as the time between the filled markers,i.e.,the end of the downstroke motion and the intersection with the static value.These are designated byT1,T2,andT3corresponding to each reduced frequency.The time lag behavior in the pressure time history atx/c=0.42 is similar to that for the lift coefficient of the entire airfoil,i.e.,the time lag decreases as increasing the reduced frequency.However,in general,the time lag behavior in the lift coefficient is not necessarily the same as that for the pressure time history on any individual position on the airfoil surface.This is especially the case for positions where flow separation is dominated.

Fig.12 Effect of reduced frequency on lift coefficient time history for case 1.

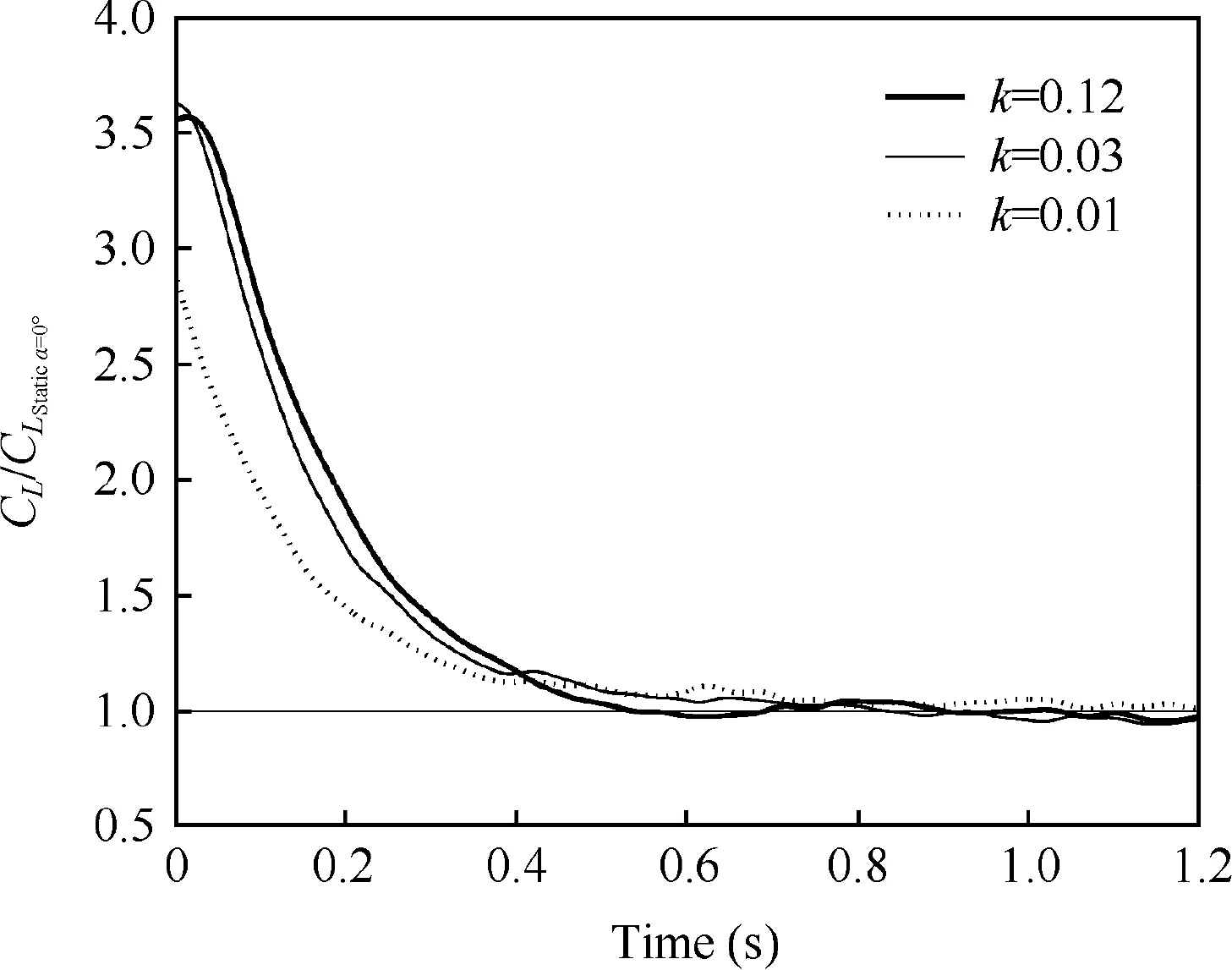
Fig.13 Illustration of the time lag in the flow field for case 1.

Fig.14 Illustration of the time lag independency of the pause duration,k=0.12.

Fig.15 Effect of reduced frequency on the pressure time history at x/c=0.42 for case 1.

4.2.Case 2(near static stall)

The stop angle in this case was set to be 10°,which is near the static stall angle of attack for this airfoil.Fig.16 shows the surface pressure distribution at four time instants,i.e.,beginning of pitch-up,beginning of pause,starting downstroke,and end of the downstroke phase where the airfoil has returned to its initial condition prior to the maneuver.The reduced frequency was 0.03,and the pause time was set as 0.2 s.

Compared with that in the previous case,a stop angle of 5°,Fig.16 shows a completely different behavior,which is supposed to be the static stall signature.However,similar to that in the previous case,the pressure distribution on the highly cambered region of the lower surface remains nearly unchanged for all of the time instances examined here.

Fig.17 shows the effect of reduced frequency on the instantaneous pressure distribution at the end of the pitch-up phase at α =10°.From this figure,remarkable differences in pressure values and their variations can be observed in comparison to those in the corresponding case at a 5°stop angle.In this case,the pressure difference between the upper and lower surfaces,especially near the leading edge,is considerably increased.Further,the pressure distribution in the highly cambered region of the lower surface is observed to be independent of the reduced frequency.However,the instantaneous pressure distribution in this region is different from the corresponding static one.

Fig.18.shows the time histories of the dynamic lift coefficient for various reduced frequencies with a pause duration 0f 0.5 s.

In the phase of pause,an oscillatory behavior is observed inCLwhich is believed to be due to static stall interferences.Note that for a 5°stop angle,as discussed in case 1,the behavior was quite monotonic with no fluctuation in the values of dynamicCLin the pause duration.In contrast to case 1,the maximum lift coefficient is achieved at the highest examined reduced frequency.

Shown in Fig.19 is the impact of reduced frequency on the time lag in the flow field for a pause duration of 0.2 s.A noteworthy problem is that the dynamicCLvalue atk=0.03 reaches the steady value prior to the other two reduced frequencies.This value for reduced frequency corresponds to a frequency of 0.96 Hz.It is likely that this value is close to the natural frequency of the system and causes resonance to happen at this frequency.Thus,the higher damping behavior in lift atk=0.03 may be attributed to the resonance phenomenon.However,no investigation has yet been performed to check the fidelity of this hypothesis.

Fig.16 Instantaneous pressure distributions in four phases of the motion for case 2.

Fig.17 Effect of reduced frequency on the pressure distribution just at the moment of pause for case 2.

Fig.18 Effect of reduced frequency on the lift coefficient time history for case 2.

Fig.19 Illustration of the time lag in the flow field for case 2.

The effect of reduced frequency on the pressure time history of a pressure port located atx/c=0.42 is shown in Fig.20.The time lag in the flow field for a stop angle of 10°,shown in this figure,is different from that explained in case 1 for a stop angle of 5°.

The values ofT1,T2,andT3suggest that the time lag behavior in the pressure time history atx/c=0.42 is similar to that for the lift coefficient of the entire airfoil in this case,and the minimum time lag is found to be fork=0.03.

4.3.Case 3(beyond static stall)

The airfoil stop angle for this case was set to 15°which is beyond the static stall.However,the dynamic stall for this airfoil during upstroke has been measured to be about 13°for a reduced frequency of 0.01 Hz.Fig.21 shows the unsteady pressure distributions at the same four time instances as in the former cases.The pause duration was set to 0.5 s.

However,in contrast to cases 1 and 2,the pressure distribution in the high-camber region of the lower surface varies with time.At time instant c,corresponding to the moment of starting pitch-down,the pressure remains almost constant within an extensive region on the upper surface.This leads to a remarkable decrease in lift during the pause phase.

This is verified by the integrated values of pressure indicating the dynamic lift coefficient,shown in Fig.22.In this case,the instantaneous values ofCLduring upstroke and downstroke intersect to form a figure ‘8” shape.The lift coefficient rapidly increases during upstroke,and the maximum dynamic lift is observed to be higher than the corresponding static value.17

In general,the dynamic stall phenomenon is much more complicated than the static stall one and depends on various parameters.Near the static stall region,as the angle of attack further increases,a signature of flow reversal can be identified near the trailing edge.This flow region moves towards the leading edge as increasing the angle of attack.The flow remains attacked to the surface as long as the boundary layer thickness in the rear part of the airfoil is not remarkably thick.Initial evidences of vortex formation can be observed as the boundary layer thickness near the leading edge is significantly increased and a shear layer is formed downstream towards the trailing edge.The leading-edge vortex grows and moves downstream accordingly as increasing the angle of attack.18,19

As a result,the suction pick in the pressure distribution moves toward the trailing edge.The maximum lift is achieved when the leading-edge vortex is well developed and located close to the surface.As the angle of attack increases,the leading-edge vortex detaches from the surface approximately at the mid chord at a certain angle of attack.This is the dynamic stall onset which is followed by a drop in the lift coefficient.4,20

As the upstroke motion proceeds,the decreasing trend ofCLcontinues up to the pause phase.When the airfoil suddenly stops,the leading-edge vortex separates from the surface,and the trailing-edge vortex is generated at the same time.However,the process interrupts as the airfoil proceeds with the downstroke motion.The decrease in lift during pause and pitch-down indicates that there still exist some local regions of separated flows on the airfoil.5,9,12

Fig.20 Effect of reduced frequency on the pressure time history at x/c=0.42 for case 2.

Fig.21 Instantaneous pressure distributions in four phases of the motion for case 3.

Fig.22 Hysteresis loop of the lift coefficient,k=0.01,pause duration=0.5 s.

Shown in Fig.23 is the instantaneous pressure distributions at the moment of pause at α =15°for two reduced frequencies and a pause duration of 0.5 s.The corresponding static values are also included for comparison.

Similar to those of the former cases,the pressure distribution in the high-camber region of the lower surface is not significantly affected by a change in the reduced frequency.However,a remarkable difference is observed between the pressure distribution in this region and the corresponding static value.The pressure distribution for this pause angle is also completely different from those of the two previous cases in static-stall and below-stall regions.

Fig.24 shows the hysteresis loops of the lift coefficient with the instantaneous angle of attack at a pause duration of 0.2 s.For the two lower reduced frequencies,k=0.01 and 0.03,at the beginning of pause,the instantaneous lift is higher than the static one.Examining the pitch-up motions,the dynamic stall evidences can only be found fork=0.01 that is the lowest reduced frequency considered in this figure.10

The time histories of the lift coefficient for three values of reduced frequency are shown in Fig.25,with a pause duration of 0.5 s.

The lift coefficient during pitch-down is observed to be oscillatory at the lowest reduced frequency.The secondary and sometimes the next series of the vortices generated during the pitch-up and pause phases are likely to be responsible for this oscillatory behavior.12The time lags in the flow field for different reduced frequencies are shown in Fig.26 with a pause duration of 0.5 s.Similar to that in case 1,the time lag decreases as increasing the reduced frequency.

Fig.23 Effect of reduced frequency on the pressure distribution just at the moment of pause for case 3.

Fig.24 Effect of reduced frequency on hysteresis loop of lift coefficient.

Fig.25 Effect of reduced frequency on lift coefficient time history for case 3.

Fig.26 Illustration of the time lag in the flow field for case 3.

Fig.27 Effect of reduced frequency on the pressure time history at x/c=0.42 for case 3.

Shown in Fig.27 are the pressure time histories atx/c=0.42 for three different reduced frequencies.The time lag for a stop angle of 15°is similar to that observed for a stop angle of 5°in case 1,i.e.,the time lag decreases as increasing the reduced frequency.

5.Conclusions

(1)It has been found that the instantaneous pressure,the time lag in the flow field,and the shape of the hysteresis loops are strongly influenced by the reduced frequency and pause angle.

(2)The time lag has also been found to be independent of the pause duration.

(3)At pause angles below and near static stall,the hysteresis loops are in the form of closed inclined curves.However,for a post-stall pause angle,the values of surface pressure during upstroke and downstroke intersect,and the hysteresis loops show a figure ‘8” shape.

(4)In the pause phase,for below-and near-stall pause angles,the lift coefficient continues in the same trend as during pitch-up,and it still increases with time during pause,while for a post-stall pause angle,the lift decreases in the pause duration for all cases.

(5)The results show that for pause angles below and beyond static stall,the time lag decreases as increasing the reduced frequency.This is supposed to be due to an increased dissipation in fluid energy at high frequencies.

(6)If the stop angle is set to the value corresponding to static stall,a different pattern was observed.At a certain reduced frequency,probably the frequency of resonance,the minimum time lag to recover to the steady state was observed.It seems that this is due to interaction of static stall with the unsteady motion and dynamics of the airfoil structure.

(7)For a beyond-static stall pause angle,dynamic stall was observed at the lowest reduced frequency.The maximum lift in a dynamic stall condition has been found to be higher than the corresponding value in static stall.

(8)For a beyond-static stall pause angle,as the reduced frequency increases,the maximum lift was postponed to higher angles of attack,and dynamic stall was not observed on the airfoil within the test conditions examined in this paper.