An efficient analytical homogenization technique for mechanical-hygrothermal responses of unidirectional composites with applications to optimization and multiscale analyses

Guannan WANG

Mechanical Engineering Department,Texas Tech University,Lubbock,TX 79409,USA

Abstract The elasticity-based Locally Exact Homogenization Theory(LEHT)is extended to study the mechanical-hygrothermal behaviors of unidirectionally-reinforced composites.Based on the framework developed previously,thermal and moisture effects are incorporated into the LEHT to study the homogenized and localized responses of heterogeneous materials,which are validated using available analytical and numerical techniques.The LEHT programs are then encapsulated as subroutines with Input/Output(I/O)interfaces,to be readily applied in different computational scenarios.In order to illustrate the efficiency of the LEHT,the theory is firstly coupled to the Particle Swarm Optimization(PSO)algorithm in order to minimize the axial thermal expansion mismatch in hexagonal and square fiber arrays by tailoring the fiber volume fraction.The LEHT is then implemented into the lamination theory to study fabrication-induced residual stresses arising during the cool-down process which introduces local laminate stresses owing to thermo-mechanical property mismatch between plies.Both of these applications illustrate the efficiency and accuracy of the LEHT in generating effective properties and local stress distributions,making the theory a golden standard in validating other analytical or numerical techniques as well as a reliable tool in composite design and practice for professionals and non-professionals alike.

KEYWORDS Coefficients of moisture expansion;Coefficients of thermal expansion;Elasticity-based locally exact homogenization theory;Mechanical-hygrothermal behavior;Multiscale laminate analysis;Particle swarm optimization

1.Introduction

Unidirectional composites have wide-ranging applications in the aerospace industry and other related areas.Owing to tight tolerance requirements of the industry,it is critically important to understand the complicated behaviors of developing fiber/-matrix material systems,such as effective properties and stress distributions that may arise from mechanical as well as thermal and moisture loadings.During the past fifty years,several analytical models have been developed to predict the effective properties of unidirectional composites,some of which have been successfully applied to engineering simulations and designs.However,most of them are based on the average matrix stress assumption(Mori-Tanaka model)or ignore the fiber- fiber interaction(CCA model),1thereby prohibiting accurate recovery of local stress distributions that are important in failure analysis or in some cases prediction of accurate effective properties.Thus,more and more researchers have been paying attention to numerical simulations because of the extensive development of computing technologies and widely applicable commercial packages(ANSYS or ABAQUS).However,largescale computations with attendant time-consuming pre-and post-processing,and demands on CPU processors placed by numerically based computational models make them less efficient in multi-scale modeling and optimization or relative applications.

Owing to the above considerations,an elasticity-based Locally Exact Homogenization Theory(LEHT)has been developed in a sequence of contributions by Pindera and co-workers.2-6The LEHT has several advantages relative to other homogenization approaches,such as convenient implementation,easy execution,and quick convergence without sacrificing accuracy in generating both homogenized moduli and localized stress distributions.These characteristics cannot be easily matched by other classical analytical methods or numerical techniques.The LEHT has proven itself as an accurate,stable,and quick-converging theory7in simulating various aspects of the mechanical behaviors of unidirectional composites,including interphase,5viscoelasticity,6optimization,8multiscale analysis,8,9surface energy,10amongst others.In this contribution,the ease of further extending the theory is illustrated in order to understand the effects of temperature and moisture,in addition to mechanical loads,on the responses of unidirectional composites,which cannot be efficiently achieved by strictly numerical codes such as ABAQUS or ANSYS.

Thermal expansion plays an important role in affecting the responses of composite materials,especially when they are employed in designing and fabricating laminates.Many analytical models11-18and Finite Element(FE)-based numerical techniques19-21possess this capability with different levels of accuracy and efficiency.Karadeniz and Kumlutas19presented a detailed review of several analytical models,and proposed a numerical study using the FE program ABAQUS.Karch20also presented a review of several models for predicting the Coefficients of Thermal Expansion(CTEs),and calculated thermal effects in composites with arbitrary geometrical inclusions using FE analysis.Based on the author's observation,only the CCA model of Rosen and Hashin15and FE results19,20have significantly better agreement in predicting transverse CTEs with experimental data,relative to the rule of mixtures as well as the equations proposed by van Fo Fy,11,12Schapery,13Chamberlain,14Schneider,16and Chamis,17while almost all of the models generate accurate results of axial CTEs.

The moisture-induced expansion response with concomitant stress fields does not appear to be as thoroughly studied in the literature as the thermal expansion response.However,moisture absorption could have a significant impact on the mechanical behaviors of polymer-matrix composites.For example,the vacuum-induced dry-out of spacecraft composites could lead to de-focusing of optical images in telescopes or distortions of microwave signals from antennas.22Most of the investigations on moisture expansion have been conducted through experimental measurements.However,several theoretical and numerical models have also been developed to predict the homogenized moisture responses of unidirectional composites.23-28Many papers in the literature have reported that the coefficients of moisture expansion may be calculated by directly borrowing the equations for thermal expansion and replacing the notations.However,this is not accurate for composites with fibers and matrices of different moisture absorption capacities,especially when the fibers are inorganic.The Tsai-Hahn model29yields more realistic Coefficient of Moisture Expansion(CME)estimates by considering different moisture contents of fiber and matrix phases.Jacquemin et al.30studied CMEs by extending the self-consistent scheme with a hygro-elastic relationship,and obtained well-matched axial CMEs but deviated transverse CMEs compared to those of the Tsai-Hahn model.

In the present work,the LEHT is further developed in order to account for thermal and moisture effects in the presence of mechanical loading.Moreover,all of the LEHT-based programs are encapsulated so that the Input/Output(I/O)into and out of the programs may be treated as interfaces by specialists and non-specialists alike who are interested in generating accurate homogenized moduli and local stress distributions without detailed knowledge about the theoretical details.Section 2 derives a detailed theoretical framework and describes the framework with I/O interfaces,while Section 3 validates the present theory by comparing generated CTEs and CMEs against other simulation and experimental results,as well as by illustrating local stress distributions.Two applications are then introduced to demonstrate the efficiency and ease-of-use of the present theory.Section 4 couples the LEHT with Particle Swarm Optimization(PSO)to identify optimal fiber volume fractions to minimize axial homogenized CTEs for both hexagonal and square microstructures.Section 5 implements the LEHT into the lamination theory to study fabrication cool-down induced residual stresses in composite laminates,including local stress distributions.Section 6 concludes this paper.

2.Analytical framework

2.1.Problem description

Repeating unit cells with two different kinds of geometries(hexagon and rectangular(square))with continuous reinforcements( fibers)along thex1axis are shown in Fig.1,wherein the fibers are not necessarily at the centers of the microstructures.Each repeating unit cell satisfies periodic boundary conditions for both displacements and tractions(see the work of Wang and Pindera3for more detailed illustrations).

A generalized plane strain assumption is adopted in the present work,and the equilibrium equations in polar coordinates are expressed as

where σrr,σθθ,σzz,σrθ,σrz,σθzare the stress components within the cylindrical coordinate,and they have the following relationship with the corresponding strain components εrr, εθθ,εzz,εrθ,εzr,εzθfor transversely isotropic materials by considering the hygrothermal effects:

whereC11=EA+;C12=2kTυA;C22=kT+GT;C23=kT-GT;C66=GA;EA,ET,υA,kT,GA,andGTare axial and transverse elastic moduli,axial Poisson's ratio,plane strain bulk modulus,axial and transverse shear moduli,respectively;αAand αTdenote axial and transverse CTEs;βAand βTare axial and transverse CMEs;ΔTis the temperature change;ΔMis the percent moisture(by weight)absorbed.It is easily noticed in Eq.(2)that thermal and moisture effects are uncoupled from mechanical(axial and transverse)shear stresses.

Following the homogenization theory framework,the total displacement fieldui（x，y）in each phase is expressed in terms of the average part(¯ε)and fluctuating part（y）caused by material inhomogeneity as

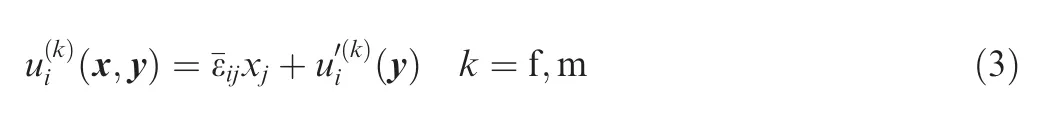
where ‘f”and ‘m” represent fiber and matrix,respectively.

Combining the local equilibrium equations,stress-strain relations,and strain-displacement relations yields the Navier's equations3in terms of the fluctuating displacements as

where ξ=r/ais a non-dimensionalized parameter,andais the radius of the fiber.The eigenvaluespnjin Eq.(5)are

with the corresponding eigenvectorsbeing

The traction components are then calculated using straindisplacement and stress-strain relations as follows:

2.2.Continuity conditions

The stress continuity and traction reciprocity lead to continuity conditions for fluctuating displacements and stresses that are expressed as

from which the coefficients associated with the matrix phase are expressed in terms of the fiber coefficients and macroscopic averaging strains for different harmonic numbers.

and the Kronecker delta δn2term is present because the average strains are introduced only through then=2 terms.The corresponding out-of-plane relationships are expressed as

nate along the unit cell's boundary that can be obtained from Hooke's law as

where the transformations of fluctuating strains between the polar and Cartesian coordinates are expressed as follows:

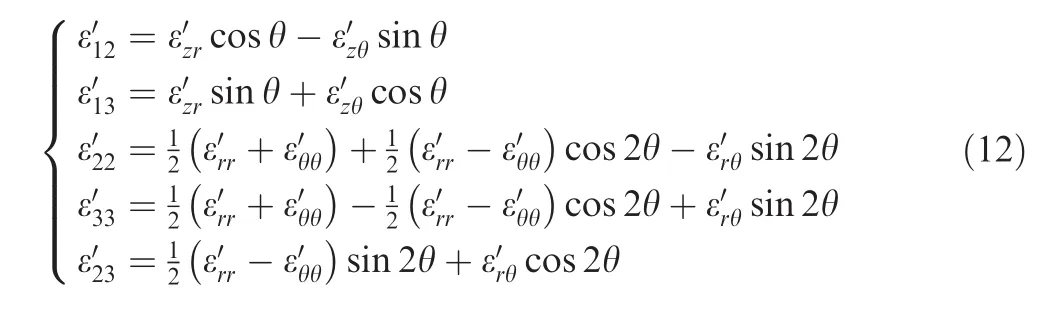
2.3.Balanced variational principle

After implementing the fiber/matrix continuity conditions,the remaining unknown fiber coefficientsare calculated by applying the periodic boundary conditions,which is accomplished using the balanced variational pri2nciple.7Firstly,the functional to be minimized is expressed as

where T=T0and u=u0are the periodic traction and displacement constraints imposed onStandSu.

Taking the first variation of Eq.(13)and considering the periodic boundary conditions yield the final systems of equations for the unknown coefficients for both rectangular(square)and hexagonal arrays3as

2.4.Homogenized constitutive equations

Once the fiber coefficientsare determined,the corresponding matrix coefficientsare calculated from the relations in Eqs.(8)-(10),which leads to the full solutions of this non-separable boundary value problem.The next step is to calculate the homogenized coefficients of hydrothermal expansions by employing the homogenized constitutive equations as

The elements of the homogenized stiffness matrix are calculated by applying one non-zero component of the macroscopic strain ¯ε in each direction at each time,and the homogenized coefficients of thermal and moisture expansions are then obtained by letting ΔTand ΔMassume nonzero values separately and calculating the corresponding average stresses in the unit cell.

Another detail that needs to be addressed is the relationship among ΔM, ΔM（f）,and ΔM（m）for polymeric composites subjected to moist environment.The moisture content in a composite is the sum of the moisture contents in both fiber and matrix phases,i.e.,

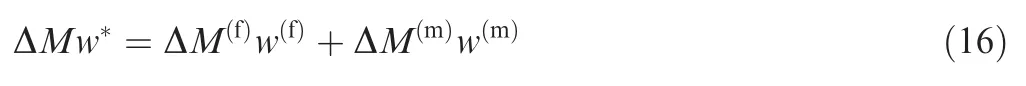
wherew（f），w（m），w*are the masses of the fiber,matrix,and composite,respectively.Inorganic fibers are assumed not to absorb any moisture so that ΔM（f）=0,and then

Since the mass is the product of density and volume,we have

Thus,the relationship for the moisture expansion between the matrix and the macroscopic level is

2.5.Encapsulation of LEHT

For structural engineers and non-specialists who want to perform structural analysis without knowing many details about micromechanical models or FE packages (ABAQUS,ANSYS),the LEHT is an efficient and robust alternative which generates accurate effective properties and localized stress distributions necessary for the applications of unidirectional composites.Fig.2 illustrates the procedure of obtaining the outputs,where users just need to focus on the I/O components and do not need to pay attention to the LEHT main body.The inputs to the MATLAB program are designed as the entries of the material and geometrical properties of the constituents(Fig.2 ‘Input” section):

Fig.2 Encapsulated LEHT program with Input/Output(I/O)interfaces.

After constructing the necessary inputs,the execution of the LEHT program is automatically conducted without concerns about mesh discretization,pre-and post-processing that are typically required in other numerical techniques,as shown in Fig.2(middle block).It should be noted that at the present stage of development,material properties of the fiber and the matrix are defined as being transversely isotropic,noting that orthotropic fiber properties are also included in this theory,4which can be readily taken into account in the future.The outputs of the program can be either the effective properties or the localized stress distributions,as shown in Fig.2(‘Output” section),depending on actual applications.

3.Validation

Elastic homogenized moduli have been extensively verified against FE and Finite Volume(FV)techniques,as well as a few other analytical techniques.3-5The convergence of the solutions was also tested.Readers are referred to the studies of Wang and Pindera3-5for more specific details.In this section,the CTEs and CMEs generated by the LEHT are validated against several analytical and numerical techniques,as well as selected experimental results.

3.1.Thermal effect

The classical Composite Cylinder Assemblage(CCA)model and FE analysis are employed for comparison of the thermal effects in composites.The CCA model with hygro-thermal effects is re-derived in Appendix A,and the FE analysis can be referred to the works of Karadeniz19and Karch.20

The axial and transverse effective CTEs are compared in Fig.3 using the following three models:LEHT,FEM(square array),and CCA model,as well as experiments.Two sets of carbon/epoxy material properties are used-T300/5208(934)and P75/934(930),whose properties are listed in Tables 1 and 2.The CTEs of both hexagonal and square arrays are calculated from the LEHT,with no noticeable difference between the two arrays,which leads to a conclusion that the geometry of microstructures has no significant effect on the CTEs.In addition,the results generated from the LEHT are observed to match well with those of the FEM18and the CCA model,15while Schapery's equations13are also used in the comparison(not shown)which yield good prediction of the axial CTEs but not the transverse components.The experimental results are also reasonably close to LEHT calculations in most cases,except the transverse CTE of P75/934 at a 0.65 fiber volume fraction,where the experiment predicts a larger thermal expansion coefficient.In general,the LEHT,FE analysis,19and CCA model15always predict better correlations with the experimental results than those by Schapery's equations and other methodologies.19

Another phenomenon that should not be ignored is the reduction of the axial thermal expansion coefficient to below zero at a sufficiently high fiber volume fraction,which means that the composite material shrinks along the fiber direction with a positive temperature change.This raises an interesting question whether we can find a proper fiber volume fraction to target zero values of axial CTEs.This is a useful and attractive composite material feature because a zero CTE will benefit high-precision instruments which need to be exposed to environments where thermal activities vary.The answer is PSO,which will be illustrated in detail in Section 4.

Besides the homogenized response,the local stress distributions are tested against the Finite Volume Direct Averaging Micromechanics(FVDAM)theory,which is an FV-based semi-analytical technique that generates accurate stress fields characterized by high stress concentrations.32-35Fig.4 compares the local stress concentrations σ22（y2，y3），σ33（y2，y3），σ11（y2，y3）calculated by the FVDAM theory and the LEHT,where only slight differences are observed.The transverse shear stress σ23（y2，y3）is also compared(not shown)with a similar outcome.

3.2.Moisture effect

In this section,the CCA model and the Tsai-Hahn model29are employed for comparison.As already mentioned,the Tsai-Hahn model29yields more realistic CME estimates when different moisture contents of the fiber and matrix phases are taken into account.For most situations where fibers do not absorb moisture,the simplified expressions of the axial and transverse CMEs are given by

where γ is a factor that stands for the ratio between water contents in the composite and in the matrix.Fig.5 compares the CMEs predicted by the LEHT,the CCA model,and Eqs.(20)and(21).The S2 glass/5208 material combination is used here(Tables 1 and 2),and the densities of glass and epoxy are 2580 kg/m3and 1380 kg/m3,respectively.It is seen that both the CCA and Tsai-Hahn models show good agreements with the LEHT in generating axial CMEs,and the geometry of the microstructure has no effect on the axial moisture expansion.However,the transverse CME predicted by the LEHT exhibits a significant deviation from the Tsai-Hahn results,while yielding a relatively good agreement with the CCA model predictions.In addition,there are also some differences between square and hexagonal arrays at large volume fractions.It should be noted that the derivation of the Tsai-Hahn model is based on the Rule-of-Mixtures(ROMs)assumption,which is a very simplified micromechanics model that ignores many basic characteristics of microstructural details,while the CCA model usually yields effective properties of high-level accuracy.4

Fig.3 Axial and transverse effective CTEs α*Aand α*Tof T300/5208 and P75/934 for different fiber volume fractions.

Table 1 Mechanical properties for calculations.

Table 2 Hygro-thermal properties for calculations.

Fig.4 Local stress comparisons σ22（y2，y3），σ33（y2，y3），σ11（y2，y3）under a unit of temperature change ΔT=1 °C between FVDAM and LEHT.

The generation of effective properties and local stress distributions using the LEHT is not only accurate but also efficient compared to commercial packages.It takes about 15 and 35 s to generate one full set of the hygro-thermal mechanical moduli for square and hexagonal microstructures,respectively,on a PC Intel(R) Core(TM) i7 CPU@3.70 GHz.In contrast,numerical techniques require a computationally costly stiffness matrix assembly,let alone pre-and post-processing in preparing and extracting data which are also extremely time-consuming and laborious.Given the LEHT's rapid development of other capabilities,this analytical technique is recommended for appropriate structural and material applications,some of which are demonstrated in the sequel.

Fig.5 Axial and transverse effective CMEs β*Aand β*Tof S2 glass/5208 epoxy for different fiber volume fractions.

4.LEHT-based PSO

PSO was developed by Kennedy and Eberhart36based on mimicking the intelligence and movement of swarms of birds or fish.The technique combines the concept of social interaction with the solution of boundary-value problems,and mimics a swarm of particles searching for a target(optimal solution)by continuously updating the swarm's(individual and collective)previous experience.Tu and Pindera37applied PSO to investigate the mechanical responses of bio-inspired material architectures.Wang et al.8,9used PSO to find the optimal parameters of functionally graded materials in the Kirsch problem to minimize the maximum values of matrix stress distributions,and demonstrated that PSO was a stable and efficient technique that could be recommended for further considerations.The details of the updating algorithm of PSO have already been introduced by Wang et al.9and are not repeated here.

As was already mentioned in Section 3,the target function is chosen as

by varying the candidate parametervfand fixing other parameters in the microstructures.Fig.6 illustrates the updating procedure of the optimization technique coupled to the LEHT program.It should be noted that the absolute values need to be rescaled by multiplying by 106because the magnitudes of CTEs are very small,which may affect the optimized results.

The search process for the minimum value is comparatively fast by just using a PC.Ten particles and ten iterations are used to generate the final results.The initial locations of the particles are in the range of[0,0.75]for both hexagonal and square arrays.From the experience of Fig.3,the optimal results can be estimated between 0.6 and 0.7,and the optimized values are obtained atvf=0.637 for the hexagonal array andvf=0.644 for the square array.The convergence at each iteration step is illustrated in Fig.7,and it can be easily noticed that 8 iterations and 5 iterations are needed to reach the optimized results for hexagonal and square arrays,respectively.The accuracy is fairly high and the errors are always below 0.2%for both arrays.The execution times for the hexagonal and square arrays are about 73 and 33 min,respectively.

Fig.6 PSO algorithm connected with LEHT.

The successful integration of PSO and the LEHT helps to identify optimized parameters that minimize axial thermal expansions.Beyond the research work done in the present example,more parameters may be incorporated as design variables to increase LEHT capabilities.8,9,37

5.LEHT-based thermal effects on composite laminates

Fig.7 Errors for PSO at each iteration step for hexagonal and square arrays.

Composite materials have significant residual thermal stresses from their fabrication procedures.In the present work,micromechanics analysis using the LEHT is extended to simulate the composite laminate cool-down process to room temperature.The cool-down process induces residual stresses in the laminate due to the mismatch of mechanical properties and CTEs of the graphite fiber and the polymer matrix.The laminate is completely free to expand,bend,and twist.However,each lamina is constrained by the adjacent laminae.Thus,the thermal stress is internal stress,and the laminate is self equilibrated.The derivation of the lamination theory necessary to follow the generated results is provided in Appendix B.

The LEHT can be easily implemented into lamination analytical algorithms to generate the homogenized plate response and local stress fields for an 8-layered symmetric quasiisotropic ［0°，±45°，90°］2composite laminate laid up with either hexagonal-or square-packed unidirectional T300 graphite/5208 epoxy plies,as shown in Fig.8,wherex-y-zare the global coordinates.Fig.9 illustrates the multiscale analysis with the LEHT block.The volume fractions of the composite layers are chosen asvf=0.637 for the hexagonal microstructures andvf=0.644 for the square microstructures,which are determined from the PSO technique from last section.The laminate is fabricated at 125°C and cooled down to room temperature 25 °C.In the ‘bottom up” process,the homogenized elastic-thermal moduli of the unidirectional plies are calculated using the LEHT based on the constituent moduli given in Tables 1 and 2.The outputs(effective properties)are then employed to calculate the reduced stiffness moduli Q（θ）of the plies used in constructing the laminate constitutive equation in the form of

Fig.8 Quasi-isotropic composite laminate with 8 plies of unidirectional-reinforced laminae.

Fig.9 Multiscale analysis connected with the LEHT program.

where（i，j=1，2，6）are the generated homogenized moduli in the local coordinate system.The stiffness moduli of other laminae in which fibers are aligned at different angles can be obtained from

in whichm=cosθ,andn=sinθ.The corresponding effective CTEs and CMEs can be calculated using

Table 3 Average stresses of 1-4 plies in global coordinates for hexagonal microstructures.

The thermal and moisture loading conditions are applied using Eq.(B6),while the strains and warping are obtained from Eq.(B7).For symmetric laminate composites,MTand MHare zero,which means that the warping deformation κ is zero.The average stress and strain distributions for each ply are obtained from Eq.(B3)in the global coordinate system,and then are transformed back to the principal coordinate as follows:

Table 4 Average stresses of 1-4 plies in global coordinates for square microstructures.

Fig.10 Comparisons of local stress distributions σ22（y2，y3）,σ33（y2，y3）,and σ23（y2，y3）within hexagonal array and square array.

The stresses in global coordinates are uniform in each ply,and their values are listed in Tables 3 and 4.Only one half of the laminate plies are illustrated as the remaining half of plies have symmetric stresses.Then the local stresses in unidirectional microstructures are calculated,illustrating the LEHT's efficient multiscale modeling capability,by applying the principal strains in the middle point of each ply.From both intuition and calculation,the principal strains are the same at all those locations,with a value of εAT= ［-0.00031，0.00233，0］Tfor the hexagonal array and εAT= ［-0.00031，0.00226，0］Tfor the square array.The local stress distributions are shown in Fig.10.In order to prove the validity of the multiscale modeling work,the average stresses in the local microstructures are also calculated: ［σ11，σ22，σ33，σ23］=[-33.933,33.906,15.415,0]MPa (hexagonal), and ［σ11，σ22，σ33，σ23］=[-34.719,34.650,13.901,0]MPa(square).As is observed in Tables 3 and 4,they are well matched.

The LEHT block is used twice in the multiscale analysis.The first pass involves calculation of the homogenized properties of all the plies.After performing the laminate analysis,the LEHT is used for a second time to generate localized stress distributions.This enables the identification of stress concentrations and hence possible damage modes.

6.Conclusions

The locally exact homogenization theory has been extended to facilitate an efficient investigation of the combined mechanical-hygrothermal responses of unidirectional composites.Moreover,the extended theory has been encapsulated as a‘black-box” with I/O interfaces in order to facilitate its use as a subroutine in larger multi-scale analysis procedures.This new homogenization tool benefits both engineers and nonspecialists who need accurate results in predicting the responses of unidirectional composites without time consuming mathematical derivations,mesh discretization,as well as pre-and post-processing intrinsic to commercial numerical packages.

The mathematical derivation of constitutive relationship and homogenization equations in the presence of combined mechanical,thermal,and moisture loads,was followed by illustrations of homogenized moduli and localized stress distributions in unidirectional composites.The CTEs generated by based on the assumption that fiber and matrix phases had different moisture absorption capabilities,and compared with CCA and Tsai-Hahn models.The fiber volume fraction was then optimized using PSO to minimize axial thermal expansion of composite materials,which might be beneficial for real designs when composites were exposed to variable temperature environments.Finally,the LEHT was implemented into the lamination theory to simulate the cool-down process during fabrications.Local stress distributions in microstructures were easily generated for both hexagonal and square arrays for comparison.

Acknowledgements

The author thanks Prof.Marek-Jerzy PINDERA of University of Virginia for helping improving the article,as well as many other valuable suggestions and advices.The author also acknowledges Dr.Wenqiong TU of Engineering Technology Associates for providing the FVDAM validation against the present work.

Appendix A

A.1.Composite cylinder assemblage model with hygro-thermal effects

The composite cylinder assemblage model was initially proposed by Hashin and Rosen38to simulate the elastic responses of unidirectional composites,and is treated as assemblages of fiber/matrix cylinders with varying sizes but fixed radius ratios.In addition,the responses of the entire domains under homogeneous boundary conditions are equivalent to the responses of each composite cylinder.Thus,an investigation of each single cylinder leads to the homogenized responses of the whole fiber/matrix domain.

Herein we start by firstly solving the existing Navier's equation of thekth constituent as

which yields the radial displacement expression:

and the corresponding stress expressions:

the LEHT were validated against the FE analysis,CCA model,as well as available experimental data.In addition,unlike most of the work reported in the literature,the CMEs were derived

It should be noticed thatB（f）=0 since the radial displacement(or stress)is bounded within the fiber domain.In order to solve the unknown coefficients in Eqs.(A2)and(A3)and generate homogenized CTEs and CMEs,the corresponding thermal or hygro loading ΔTor ΔMneeds to be applied at the fibrous composites.Since the procedures of calculating CTEs and CMEs are similar,here we just illustrate the moisture effect,which is a little bit more complicated.By applying a unit moisture loading ΔM, ΔM（k）can be easily calculated through Eq.(19),and then four equations can be established as follows:

Eqs.(A4)-(A7)help establishing the equations for the unknownsA（f）,A（m）,B（m）,and ¯εzz,from which the homogenized CMEs can be calculated as

A similar procedure can also be used for the thermal effect,and is not repeated here.

Appendix B

Here we introduce some basic equations based on the lamination theory.The terms representing the moisture effect are also included for further reference.The total strains εTotalin the laminate are the superposition of mechanical strains εMand hygrothermal strains εTand εH,which can also be expressed as

In the present example,the residual stress is just introduced through thermal stress instead of the mechanical stress,and thus the l.h.s of Eq.(B7)should equate to zeros.