Robust decentralized control design for aircraft engines:A fractional type

Muxun PAN,Lingjin CAO,Wenxing ZHOU,Jinqun HUANG,Ye-Hw CHEN

aCollege of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

bThe George W.Woodruff School of Mechanical Engineering,Georgia Institute of Technology,Atlanta,GA 30332-0405,USA

Abstract A new decentralized control for aircraft engines is proposed.In the proposed control approach,aircraft engines are considered as uncertain large-scale systems composed of interconnected uncertain subsystems.For each subsystem,the time-varying uncertainty,including parameter disturbances and interconnections in/between subsystems,is depicted by a class of general nonlinear functions.A fractional robust decentralized control with two parts,the nominal one and the fractional one,is presented.The nominal control guarantees the asymptotical stability of the engine system without uncertainty.The fractional part aims at overcoming the influences of uncertainty.Compared to the previous studies,the presented control provides not only an extra flexibility for the system performance tuning by the fraction-type gain but also a facility for the control input calculation.The proposed control approach is applied to a turbofan engine with two subsystems.The computer simulation shows that,in the flight envelope,the fractional control not only guarantees the closed-loop system uniform boundedness and ultimate uniform boundedness but also shows good economy.

KEYWORDS Aircraft engines;Large-scale systems;Robust decentralized control;Uncertainty;Uniform boundedness;Uniform ultimate boundedness

1.Introduction

An aircraft engine is a complex nonlinear plant that contains multi-subsystem.These subsystems are coupled with each other via complicated mechanical and aerothermodynamics connections.In the conventional control system design for aircraft engine,a centralized structure is generally adopted.1However,for modern advanced aircraft engines,the control variables increase to 8 and more,and the entire controlled system becomes more complex.2As indicated in Ref.3,for a complex physical configuration and high dimensionality of interconnected systems,a centralized control is neither economically feasible nor even necessary.Moreover,it requires much communication,which brings problem of bandwidth,time-delays and reliability.The simulation in Ref.1showed that when the network time-delay sufficiently increases,the instability of the engine occurs.Consequently,the decentral-ized control is a positive alternative scheme for a large-scale system,such as the control of aircraft engines,1space robot,4complex structures of building,5networks,6-8and multi-agent control.9,10The philosophy of decentralized control is to use the ‘locally available” information of each subsystem to construct a controller,which provides the benefits of weight and cost reduction and performance improvement.11Lewis12introduced the distributed control concept into the aircraft engine control.Lewis12and Behbahani et al.13analyzed and estimated successively the contribution that decentralized controls lead to thrust-weight ratio increase and cost reduction,compared to the centralized control.Perez and Lou presented that for a gas turbine engine,the interactions between the sub-loops were restrained by a frequency domain-based decentralized control,and the system could remain stable in the presence of soft and/or hard failures.14

Decentralized control has been attracting the attention of global researchers,who have produced numerous relevant literature studies.To the authors' knowledge,in this paper,we briefly review the research on the decentralized control with discrete and continuous approaches for linear and nonlinear complex/large-scale systems.For linear complex systems,one of the most popular and classic control approaches is to build interaction-oriented models and make use of different mathematical methods and graphic theories to shape closed systems with diagram or cascade forms.5,14-18For example,linear state feedback control laws based on the Lyapunov stability or the pole placement based on Nyquist stability were presented in Ref.15In Ref.14,a permutation matrix and a square down matrix were designed to shape the system transfer function with a diagonal form and reduce the interaction.In Ref.5,the decentralized cascade sliding mode control was developed for a steel frame structure.In the decentralized state feedback control design of Ref.17,an M-matrix constrained the solution of Lyapunov equation to decompose interactions.By using the graphs of the controlled complex systemGAand controllerGK,the controllability of a whole complex system based on arbitrary pole placement decentralized controllers was proposed in Ref.18.

Other than interactions,as more practical and realistic considerations,such as nonlinearity,parameter disturbance,unmodeled error,and networked time-delay,are taken into account,large-scale systems are being described in more detail.Generally,two general methods are used to consider the nonlinearity:one is to partition a nonlinear system into a linear nominal system and a nonlinear part.The nonlinear part normally can be interaction and/or uncertainty,input disturbance and time-delay terms.8,19-23Based on this strategy,a nominal controller and a compensator are designed separately for the nominal system and the nonlinear part.The upper bound of the norm of interaction terms is often adopted in the compensator design.Ref.11summarized this method's theoretical basis and its research history.Chen assumed the interaction norm bound with a one-order polynomial form and presented a robust decentralized controller.22Han and Chen extended this assumptive bound to a more general non-decreasing function.23Unlike the approach of taking advantage of the known norm upper bounds of interactions and uncertainty,Wu considered the case of unknown upper bounds,estimated these upper bounds by adaptive laws and finally proposed an auxiliary control(compensator)to overcome interactions and uncertainty.8,20Recently,beyond the partition strategy mentioned above,the approaches to consider interaction and design decentralized control are more diverse.6,7,9,24-26A local observer depending on the local control input and output has been developed.The observer output and local output constructed a completely decentralized controller.6,7,9In Ref.26,the authors demonstrated a discrete Linear Quadratic Regulator(LQR)decentralized control with partial history sharing information.To decompose the interaction,a conditional mean of the state and control input replaced the global information in the subsystem controller,and a Kalmann filter was used to update the mean.

In this paper,we present a fractional robust decentralized control.The implication of fractional is that the control gain is a fractional type with an optional order parameter(see Eq.(31)).This fractional structure contains the control form in Ref.22and provides a more flexibility for designers.Moreover,we apply this fractional control to aircraft engines.An aircraft engine is considered as a large-scale system that contains several interconnected subsystems.Because of the existence of individual difference between real engines,unmodeled dynamics,nonlinearity of dynamics and unknown disturbance,both the local subsystems and the interconnecting terms exhibit uncertainty.Based on the approach adopted in Refs.19-21,23,we describe this aircraft engine large-scale system as a nominal system and a nonlinear part.A novelty in Ref.19is that the region around the sliding mode face was defined for the compensator design.Consequently,a sliding mode controller with a continuous function but a classical discontinuous function was obtained.We notice that the nominal state is required in sliding mode compensator calculations,while for a nonlinear aircraft engine,it is difficult to obtain this nominal state.In Ref.20,because of the unknown upper bound of interaction norm and uncertainty norm,the convergent bound of tracking errors could not be obtained theoretically.In Refs.21,23,Chen and Han presented some important investigations involving the interconnection systems modeling and robust control designing processes with linear bound and nonlinear bound uncertainty;however,they did not consider the effect of control inputs in other subsystems on the studied subsystem.In our paper,we consider not only the states but also the control outputs from other subsystems as interactions of the local subsystem,and a new fractional decentralized control design approach is proposed.Here,the fractional control means that the control gain has a multi-order fractional form.By choosing different orders,a series of controller candidates are produced.

The main contribution of this new control is threefold:(A)the fractional decentralized robust control can guarantee the interconnection dynamic system uniform boundedness and ultimate uniform boundedness regardless of the nonlinear uncertainty.The calculation of control inputs only needs the system states and avoids the requirement of nominal states in Ref.19(B)the new control has a more flexible and general structure compared to Refs.22,23,which is one of the motivations of our work.Actually,the controls in Refs.22,23can be considered as a specific case(ki=1)of the presented fractional control.Moreover,designers can have more flexibility to achieve the desired performance by choosing and adjusting the order and/or parameters in the fractional control law.The third contribution is the relationship between the control law order and the control cost;a bounded region could help engineers to achieve a balance between the system performance and the control cost.

The paper is organized as follows.The problem is stated in Section 2.In Section 3,a class of multi-order robust decentralized control for nonlinear large-scale systems is proposed.We discuss the decentralized control for linear large-scale system as a special case in Section 4.In Section 5,we discuss the effect of adjustable parameters in controller law on the control cost and the bounded region.In Section 6,we apply the controller to aircraft engines,and the controller constructing process is introduced.In Section 7,the simulation results of the controlled engine system are given to illustrate the effectiveness of the proposed approaches.A brief conclusion and discussion of the results are presented in Section 8.

2.Problem statement

The system under considerationSis composed ofNcoupled subsystemsSithat are described as

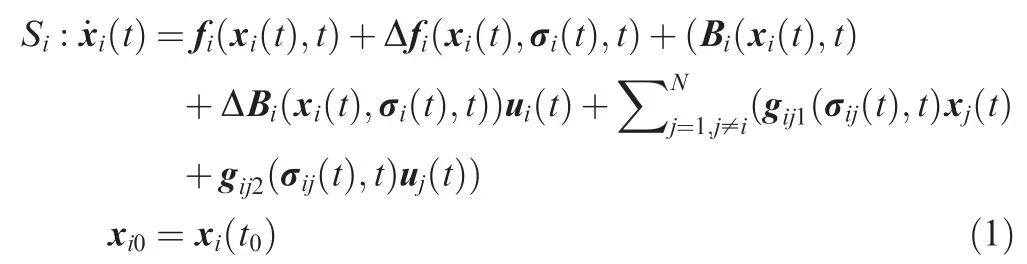
and for alli∈ ｛1，2，···，N｝.Here xi（t）∈ Rniand ui（t）∈ Rmiare states and control inputs of theith subsystem respectively,niandmiare the dimensions of xi（t）and ui（t）,σi（s）∈ Rsiare uncertain parameters,siis the dimension of σi（s）,and the third term of right side of Eq.(1)is the interconnection in theith subsystem caused by other subsystems.Unknown functions σi（·）:R → Σiand σij（·）:R → Σijare Lebesgue measurable,Σi，Σij⊂ Rsi.Furthermore,the known function fi（·）:Rni×R → Rniand Bi（·）:Rni× R → Rni×mi,and the(known or unknown)functions Δfi（·）:Rni× Σ × R → Rni, ΔBi（·）:Rni×Σ × R → Rni×mi, gij1（·）:Σij× R → Rni×njand gij2（·）:Σij×R → Rni×mjare Lebesgue measurable intand continuous in other arguments.

By Eq.(1),the large-scale systems can be written as

From Eq.(1),we can see that each subsystem is divided into three parts:the internal dynamic system fi（xi（t），t）,control term Biuiand uncertainty terms(which contain interconnection terms).Now we pose some assumptions on this largescale system.

with xi=0 as its global equilibrium position.Furthermore,there exist a functionVi（·）:Rni× R → R+and strictly positive scalar γ1i,γ2iand γ3i,such that

are met for all（xi，σi，t）∈ Rni× Σi× R,（σij，t）∈ Σij× R.λmin（·）denotes the minimum eigenvalue of matrix （·）.

Remark 1.In Assumption 1,the nominal system is the system without uncertainty.The control qi（xi，t）which will be the first part of our robust decentralized controller guarantees the stability of nominal system.Assumption 2 is the matching conditions.Assumption 3 prescribes the bounds of uncertainty and interconnection terms,and the functions ζ1i（xi，t）,ζ2i（xi，t）,and ζ3i（xi，t）can have more general forms.

Moreover,we state two definitions of performance parameters that we pursue.

Given constantr0∈ （0，∞）,system Eq.(24)is uniformly bounded,if there exists a positive constantd（r0）＜ ∞ such that

Definition 2.Given constants¯r＞r,r＞0 andr0＞0,system Eq.(24)is uniformly ultimately bounded if

3.Fractional robust decentralized control for nonlinear largescale systems

Before the presentation of the main results,we make the following preparation.We define continuous functions αi（·）:Rni× R → Rmiand ψi（·）:Rni× R → R+(i=1，2，···，N),as

where δij＞ 0,ri＞ 0 andujmax=maxt∈［0，∞）‖uj（t）‖.Furthermore,there always exist δijsatisfying

By combining Eqs.(27)and(28),we define the following function Ψi（·）:Rni× R → R+as for all（xi，t）∈ Rni× R（i=1，2，···，N）.

By Eq.(12),Eq.(27),Eq.(28)and Eq.(30),our new fractional robust decentralized control is

where

where εi＞ 0,andkiis a strictly positive integer(i.e.,ki=1，2，···).

By choosing different controller orderki,we can obtain a different control law.Letki=1，2，3,and thus the fractional parts of corresponding 1st,2nd,and 3rd order controller are

Remark 2.Because Ψi≥ 0,for all εi＞ 0,

By Eqs.(23)and(36),it is easy to determine that the denominator of Eq.(32)is greater than zero,which means that the fractional parts of controllers Eq.(31),kipi（xi，t）,always exist for any finite （xi，t）.

Remark 3.The fractional part of the new robust decentralized controllerkipi（xi，t）can be considered as the composition of two parts.The first part,

implies the control direction.The second part is a fractional gain defined as

Note that both the numerator and denominator of τiareki-1 order polynomials.Whenki=1,the controller has the same structure as that in Ref.22.The controller in Ref.22can be considered as a specific form of Eq. (32). The order of polynomial and the parameter can be adjusted, thus providing a flexible control scheme for designers to obtain better dynamic performance.For example,when each subsystem has different internal dynamic performance,one can achieve the desired performance of the control system by choosing differentkiand εi.

Theorem 1.Consider system Eq.(2)subject to Assumptions1-3.Under controller Eq.(31),the controlled system is uniformly bounded and uniformly ultimately bounded.For given r0and¯r,

Proof of Theorem 1.See Appendix A.□

Remark 4.We discuss the effect of parameters εiandrion the system performance and the control.According to Eqs.(39)and(40),the size of the uniform boundedness region will increase with the increase in εiand decrease with the increase inri.Moreover,by Eqs.(28)and(32),the control cost will decrease with the increase in εiand increase with the increase inri.These observations suggest that larger εi,smallerri,or larger εi/riwill bring larger size of the uniform boundedness region and smaller control cost.

We now briefly summarize the procedure of the robust decentralized controller as follows:

Step 1.By Eqs.(19)-(23),decide and calculate ζ1i≥ 0,βij≥ 0(i=1，2，···，N), ζ2i≥ 0, ζ3i≥ 0(i=1，2，···，N,j=1，2，···，N).

Step 2.ChooseViin Eq.(13)and calculate ∂Vi/∂xi.

Step 3.Calculate αiin Eq.(27).

Step 4.Give δij＞ 0(i，j=1，2，···，N)andri＞ 0(i=1，2，···，N).Calculate ψiin Eq.(28)based on results of Step 1.

Step 5.Based on αiand ψi,calculate Ψiin Eq.(30).

Step 6.Chooseki≥ 1(i=1，2，···)and εi＞ 0(i=1，2，···，N).Calculate the fractional robust decentralized control in Eq.(31).

4.Robust decentralized control design for linear large-scale systems

In Section 3,the new robust control for non-linear large-scale systems is proposed.In this section,we will discuss one of its special cases:the control design for linear large-scale systems.

where λmin（·）and λmax（·）are the minimum eigenvalue and maximum eigenvalue of a matrix respectively.According to Eqs.(47)and(48),one easily determines,for subsystem Eq.(44),that Assumption 1 is met.

Consider Eqs.(15)-(18)and(44),and define

and then Assumption 2 is met.

For Assumption 3,the bounds of uncertainty and interconnections are rewritten as

Consequently,the parameters in Eqs.(27)-(30)are calculated by

where δij＞ 0,ri＞ 0,andi，j=1，2，···，N.For subsystem Eq.(44),the fractional control part of Eq.(31)is updated to

Finally,by combining Eqs.(45)and(62),the fractional robust decentralized controller for linear large-scale systems is

5.Analysis of parameters in fractional robust decentralized control

One of the initial motivation of our fractional control is to enhance the flexibility of performance adjustment.We achieve this goal via introducing parameters:the order of control lawkiand gain parameter εi.In the sense of differentki,we intend to provide a series of controllers that render the different dynamical subsystems with the different controllers under the similar structure frame to obtain satisfactory performance.In this section,the investigation into the effect of the orderkiand parameters εion the control cost and bounded region is conducted.By Eqs.(31)and(38),we know

Lemma 1.For anyεi＞ 0, Ψi＞ 0and ki=1，2，···,the magnitude ofτi（ki，εi，Ψi）andΔτi（ki，εi，Ψi）decrease with the increase in ki.

Proof of Lemma 1.See Appendix B.□

Remark 5.Because the magnitude of the decentralized robust control Eq.(31)is in proportion to|τi（ki，εi，Ψi）|,the magnitude of the control decreases with the increase inki,that is,the control effort is smaller with largerki.It will help to save the control cost with largerki.However,with the increase inki,the control scheme becomes increasingly complex and thus requires more calculation.Therefore,the choice ofkiis a trade-off design,which depends on the practical engineering application.

Lemma 2.For anyεi＞ 0,Ψi＞ 0,and ki=1，2，···,the magnitude ofτi（ki，εi，Ψi）decreases with the increase inεi/Ψiand

Proof of Lemma 2.See Appendix C.□

Remark 6.By Eqs.(28)and(30),one knows that ψiis proportional tori,i.e.,a smallerriwill result in a smaller ψiand Ψi.This also results in the conclusion in Remark 4,namely,larger εiand smallerriwill result in smaller control cost.

6.Robust decentralized control design for aircraft engines

For a turbofan engine,its dynamic characteristic can be depicted by

Where xT（t）=［nL（t） πT（t）］is the state variable of a turbofan,uT（t）= ［Wf（t）A8（t）］is the control variable,and f（·）is a nonlinear function.nLis the rotational speed of lowpressure spool,πTis the turbine pressure ratio,Wfis the fuel flow,andA8is the exhaust nozzle.By the small perturbation method or/and the least square fitting algorithm,a linear model of the turbofan is extracted from Eq.(66).

Here A ∈ R2×2,and B ∈ R2×2.

Assume that the uncertain dynamic turbofan system Eq.(67)can also be described as

whereaij=¯aij+Δaij,bij=¯bij+Δbij(i，j=1，2),A=［¯aij］2×2,ΔA=［Δaij］2×2,B=［¯bij］2×2,and ΔB=［Δbij］2×2.

System Eq.(68)can be regarded as the composition of the following two single-input single-output subsystemsS1andS2:

For a turbofan engine,the fractional part of robust decentralized control is

Remark 7.For a turbofan engine,because its nominal subsystem is stable,the control partKixi(i=1，2),is neglected here.

The aircraft engine robust decentralized control system is shown in Fig.1.In the Fig.1,the coupling uncertainty between the subsystem 1 and the subsystem 2 is represented by Δ12and Δ21.According to Eqs.(75)-(79)and combining the aircraft engine linear model,the parameters β12, β21, ζ11,ζ12, ξ12,and ξ21can be derived first.Next,according to Eq.(82)and the parameters given by the designers,ψ1and ψ2are derived.At every step in the simulation,the state variablesx1andx2will be updated and the parameters α1and α2will be updated.Subsequently, Ψ1and Ψ2are calculated at every step in the simulation.By Eq.(84),the robust decentralized controller is obtained.

Fig.1 Robust decentralized control system of turbofan engine.

7.Simulation and result analysis

In order to conduct computer simulations of theu2max=0.1,δ12=3×10-4,δ21=100,r1=2×10-3,r2=80,ε1=5 × 10-3,and ε2=1 × 10-5.The simulations are performed in the flight envelope depicted in Fig.2,which is formed by the flight heightHand the Mach numberMa.We notate the number of the operation points in Fig.2 asNOP.Hence,NOP=18.Because of space limitation,the simulation results at the point 1,9 and 14 are given in Figs.3-8.From these figures,we can see that the 1st,2nd,3rd order control can guarantee the desired performance.With the increase of order,the dynamic responses become slightly lower.To compare the performance between the new control and the dominated control,we design a PI control for the same turbofan Eq.(68)withKp1=9×10-4,Ki1=5×10-5,Kp2=8×10-3,andKi2=0.02.The simulation results at the corresponding operation points are also depicted in Figs.3-8.Fig.3 shows that the responses ofnLand πTunder the four controllers are similar.At point 14,there is no overshoot ofnLunder the 2nd order control,and the overshoot ofnLunder PI control is 17.838%.Such overshoot is not acceptable for a turbofan engine.

Fig.2 Simulation point positional distribution.

We define the integral of control effortCto evaluate the economic efficiency of the controlled system.The control cost sketch map is shown in Fig.9.For the fuel consumption,whenWfis greater than its baseline value,the fuel is consumed.Conversely,ifWfis less than the baseline value,this part of fuel should be cut from the baseline value.Thus,CforWfis defined asCWf=C1-C2.For the tuning of nozzle areaA8,regardless of whether the area is larger or smaller than the baseline value,the hydraulic energy is consumed to adjustA8.Thus,CforA8isCA8=C1+C2.Here,the settling timets,the overshoot δ andCare adopted to evaluate the system behavior.We compare the system responses under the 2nd order control and the PI control.Figs.10-12 give the statistics of performance index comparison at all eighteen points,and the magnitude between the minimal and maximal performance indices are listed in Table 1.

Fig.3 Responses of states at point 1.

Fig.4 History of controls at point 1.

Fig.5 Responses of states at point 9.

Fig.6 History of controls at point 9.

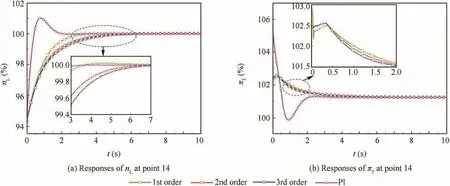
Fig.7 Responses of states at point 14.

Fig.8 History of controls at point 14.

Fig.9 Sketch map of control cost.

Figs.10-12 and Table 1 show that(A)as far astsofnLand πT,at part of the simulation points,such as points 10,14,17 and 18,tsunder 2nd order control is larger than that under PI control,and opposite situation appears at the other part of simulation points;and(B)checking δ andCat the same time,δ andCunder the 2nd order control are much less than those under the PI control.For example,the maximal δ ofnLand πTunder the PI control reach 17.838%and 28.1552%respectively.(C)With the increase of order,the value oftsof the controlled system increases gently,while δ of the controlled system decreases obviously.

The above analysis implies that designers could obtain the satisfied turbofan dynamic behavior and economical cost by determining the appropriate fractional control.The comparison between the fractional control and the PI control shows that the fractional control guarantees better comprehensive performance.

Fig.10 Settling time of state response at all 18 operating points.

Fig.11 Overshoot of state responses at all 18 operating points.

Fig.12 Cost of control at all 18 operating points.

Table 1 Performance index extremes of outputs under different conditions and different controls.

8.Conclusions

The problem of control design for an uncertain turbofan system which is composed ofNsubsystems was considered.Each subsystem not only contains internal uncertainty but also has external uncertainty,which is nonlinear and time-varying.A fractional robust decentralized controller was presented.By choosing the controller parameter and order,more flexible candidate controllers can be obtained.By analyzing the relationship among the control order,control cost and boundedness region,we provide designers the reference on achieving balanced trade-off between the performance and control cost.The new decentralized control design was applied to the turbofan control system with two subsystems.The computer simulation demonstrates that the proposed control guarantees the uniform boundedness and uniform ultimate boundedness of the controlled system and better comprehensive performance than the traditional PI control.

Acknowledgement

This work was supported by the Fundamental Research Funds for the Central Universities,China(No.NJ2016020).

Appendix A.

Proof of Theorem 1.Select Lyapunov candidate functionV（·）:Rn× R → R+as

HereVi（xi，t）is the same as the function in Assumption 1.As a consequence of Eq.(13),

For simplicity,some arguments will be omitted as long as no ambiguity arises.

Consider all terms of Eq.(A6).As a consequence of Eq.(14),

By Eqs.(19)and(27),the third term in Eq.(A6)satisfies

Combining Eq.(27),Eq.(30)and Eq.(31),the fourth term in Eq.(A6)is

By Eq.(23),one obtains

Relating Eq.(A10),Eq.(A9)can be rewritten as

Combining Eqs.(20),(21),(27)and(28),the last three terms in Eq.(A6)satisfy

Combining Eqs.(A7)-(A12),Eq.(A6)can be rewritten as

We further consider the second term of the right-hand side of Eq.(A13).By using the equationak-bk= （a-b）（ak-1+ak-2b+ ···+bk-1）（a，b∈ R）for any ε＞ 0,we have

Therefore,Eq.(A13)can be rewritten as

Based on Eq.(A5),Eq.(A25)and Lemma 1 in Ref.23,system Eq.(2)is uniform boundedness and uniform ultimate boundedness.From Eq.(A5),Eq.(A25)and Eqs.(14)and(15)in Ref.23,we know that the relevant parameters are

Therefore,the increment Δτi（ki，εi，Ψi）decreases with the increase inki.

Appendix C