三柱门架墩结构抗震分析研究
2019-02-27高涛
高 涛
(北京建达道桥咨询有限公司 北京市 100015)
门架墩占用空间少,对于跨线桥梁以及下部墩柱位置受限区域优势明显,可以避免上部大跨结构、节省造价。尤其在城镇化程度高、对桥下空间综合开发利用要求高的地区已得到了广泛的应用。
1 工程概况
中山西环高速公路位于珠三角区域的广东省中山市,常规路段上部结构采用30m、35m跨径先张法Bulb-T梁,下部结构采用独柱墩、双柱墩及三柱门架墩。对其中的跨径为35m标准工字梁桥进行抗震验算。主要技术标准如下:
跨径:3×35m(一联); 桥墩结构:三柱式桥墩;设计速度:100km/h;支座类型:GJZ400×450×99型板式橡胶支座; 桥面宽度:2×16.25m;地震烈度:基本烈度为Ⅶ度,地震动峰值加速度为0.1g,按Ⅷ设防;设计荷载:公路I级;行车道数:双向六车道; 设计使用寿命:100 年。
桥墩一般构造如图1所示,其中中墩为2m×2m方墩,配2排28号钢筋,边墩为直径1.6m圆墩,配一排半32号钢筋;桩基直径1.8m,配一排32号钢筋。
2 抗震性能要求
2.1 性能要求及验算指标
参照《公路桥梁抗震设计细则》(JTG/T B02-01-2008)规定,本桥属于A类桥梁。抗震设防目标为:当桥梁遭受E1地震作用时,桥梁不受损坏或不需修复即可使用;当桥梁遭受E2地震作用时,桥梁可发生局部轻微损伤,不需修复或经简单修复可继续使用。
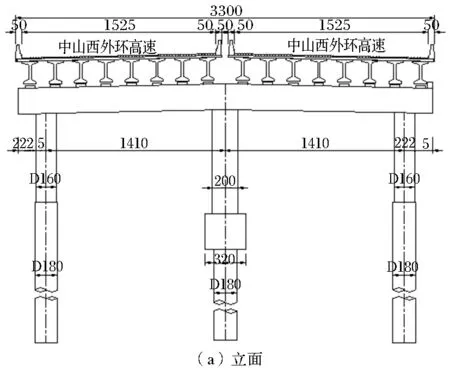
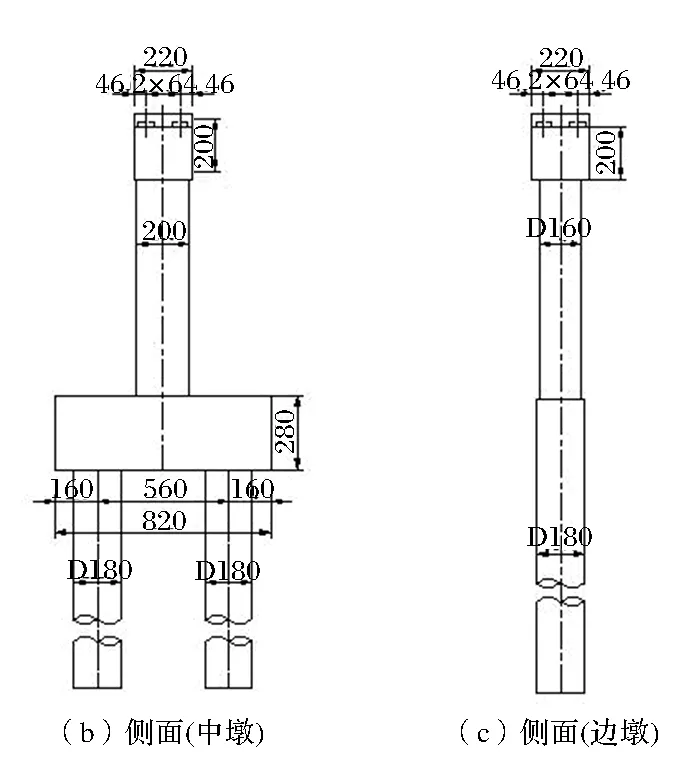
图1 桥墩一般构造图(单位:cm)
2.2 抗震验算方法
抗震验算包括抗弯和抗剪两部分。
(1)抗弯验算方法
按照《公路桥梁抗震设计细则》规定,核心混凝土采用Mander模型,钢筋采用双线性应力-应变关系。采用软件midas/civil内部计算关键截面的弯矩-曲率曲线,得到钢筋混凝土构件的首屈弯矩和等效屈服弯矩。
(2)抗剪验算方法
详见下文塑性阶段验算的剪力验算。
2.3 地震作用
考虑顺桥向、横桥向及竖向地震作用,分别进行反应谱和时程分析。本桥抗震设防类别为A类,E1地震取重现期为475年地震动,E2地震取重现期为1975年地震动。根据一般场地条件,确定基本烈度为Ⅶ度。
在《工程场地地震安全性评价报告》中,采用基岩地震动加速度反应谱衰减关系,对各周期点进行概率危险性计算,得到中山西环高速公路50 年超越概率水平为 10%(重现期约 475 年)和 2.5%(重现期约 1975 年)的基岩地震动加速度反应谱。在报告中,按照地震安全性评价Ⅱ级工作的技术要求,对 100 年超越概率水平为 63%、50年超越概率水平为10%和2.5%分别给出工程场地六条人造基岩地震动的随机样本时程,根据规范要求,本桥取前3条地震动时程进行抗震分析。E2作用下反应谱曲线和部分地震动时程分别如图2、图3所示。

图2 地震动反应谱(重现期1975年)

图3 地震动时程波(重现期1975年)
3 桥梁模型
建模计算采用有限元软件MIDAS/civil程序进行,模型均为梁单元。整体计算模型如图4所示。模型关键位置图见图5。

图4 整体模型图
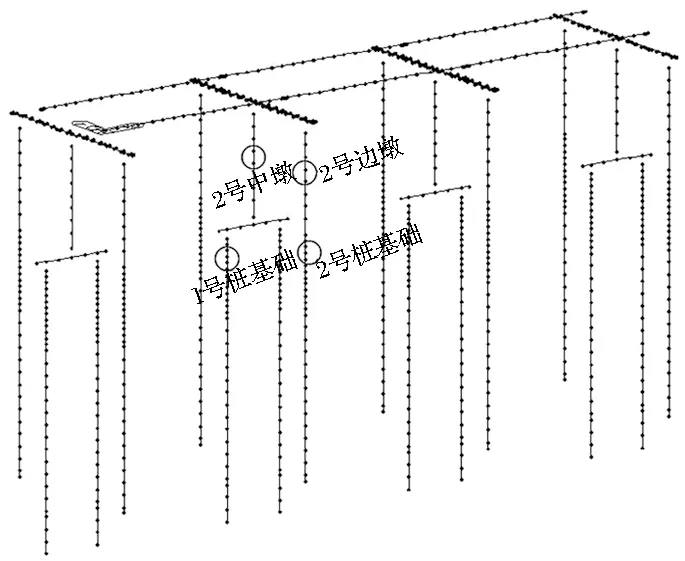
图5 模型关键位置图
3.1 边界条件
横向挡块应用一般连接中的间隙单元模拟,板式橡胶支座采用一般连接中的滞后系统模拟非线性,支座具体数据如表1所示,本模型考虑桩土的共同作用,用点弹簧模拟桩的边界条件,土弹簧水平刚度采用表征土介质弹性值的m参数计算,动力计算m取值为静力时的2.5倍。竖向刚度根据摩擦桩承载力进行估算,同时桩底固结。

表1 支座数据表
3.2 塑性铰单元
时程分析时,对于可能发生塑性变形的单元即桥墩单元采用纤维单元模拟,桥墩单元截面如图6所示。


图6 纤维单元图
3.3 荷载组合
组合1:1.0×自重+1.0×竖向地震力Ez+1.0×横桥向地震力Ey;
组合2:1.0×自重+1.0×竖向地震力Ez+1.0×顺桥向地震力Ex。
4 反应谱分析
为满足本桥“小震不坏,大震不倒”的抗震设防目标,应分别进行E1作用下的强度计算和E2作用下的延性计算。鉴于本桥由静力计算所确定的截面尺寸较大,经试算,E1作用下强度满足要求,且具有较大冗余度。依据E1地震响应计算数据及长期设计经验,在该截面尺寸下,桥墩仍有可能在E2地震作用下保持弹性。抗震性能验算中,假设在永久作用+E2地震作用下桥墩仍处于弹性状态,不对其截面刚度进行折减,计算桥墩关键截面是否仍保持弹性。
根据规范要求,多柱式桥墩抗震验算时,横桥向地震作用下需要验算墩顶和墩底截面,顺桥向地震作用下验算墩底截面。本桥沿中跨跨中和桥梁中心线对称,所以只验算2号桥墩中墩和边墩及下部的①②号桩基础详见图5。本桥的反应谱分析验算考虑两种最不利的工况,即关键截面处的最大轴力及对应的最大弯矩和最小轴力及对应的最大弯矩。
E2地震作用下横向和纵向关键截面处内力验算结果如表2所示。
计算结果表明,E2地震作用下桥墩截面仍保持为弹性,不再进行塑性验算。同时,反应谱计算表明:弯矩一致情况下,较小轴力的工况控制计算。
5 时程分析
关键验算截面与反应谱分析相同。首先考虑E2作用下的3个地震波在各关键截面所产生的最不利弯矩M,然后根据弯矩曲率关系数值分析求得轴力作用下的等效屈服弯矩My,如果My大于M,则需要进一步做塑性分析。

表2 E2地震作用下关键截面处内力验算结果
E2地震作用下横向和纵向关键截面处内力验算结果如表3所示。
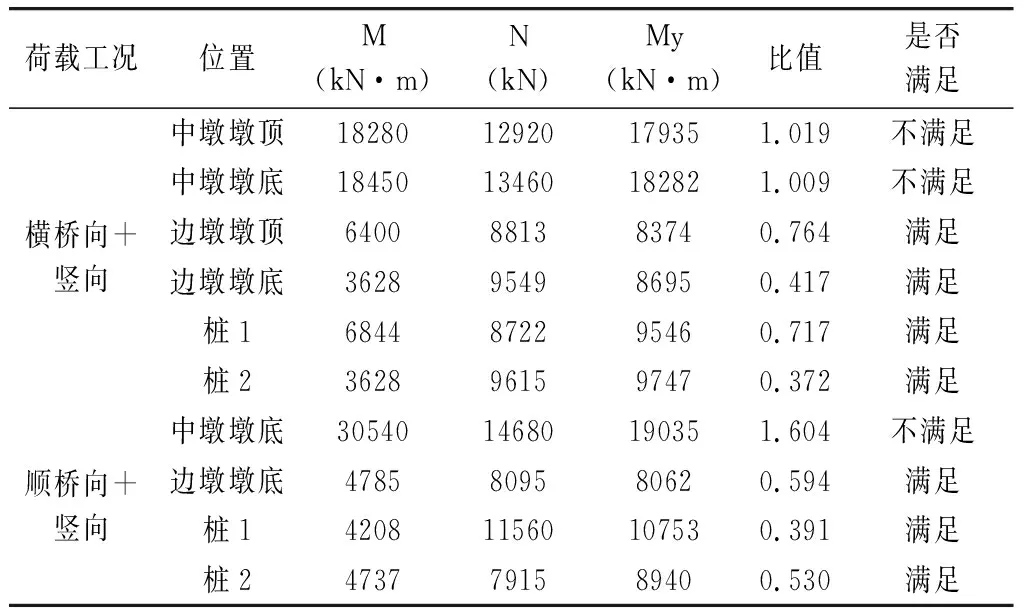
表3 E2地震作用下关键截面处内力验算结果
E2地震作用下,弹性阶段不满足要求,中墩的墩顶及墩底在横桥向和顺桥向进入塑性阶段,需要进行塑性验算。塑性阶段验算如下:
(1)剪力验算
根据规范要求,墩柱塑性铰区域沿顺桥向和横桥向的斜截面抗剪强度应按下列公式验算:
桥墩横向和纵向剪力计算结果如表4所示:

表4 剪力计算结果
计算结果表明:桥墩横向和纵向抗剪计算满足要求。
(2)桥墩墩顶位移验算
根据抗震规范要求,顺桥向容许位移按下式计算:
横桥向的容许位移采用PUSHOVER方法计算,建立三柱墩模型,定义桥墩墩顶和墩底为六个塑性铰区域,保持上部恒载压力不变,施加水平荷载,当墩柱的任一塑性铰达到其最大容许转角时,盖梁处的横向水平位移即为容许位移。
桥墩横向和纵向位移计算结果如表5所示。
计算结果表明:横向和纵向位移验算均满足要求。
6 结论
(1)E2地震作用下,反应谱分析桥墩在弹性范围之内,未进入塑性阶段,满足抗震要求;时程分析则进入塑性阶段,需进行塑性铰抗剪和位移验算,满足抗震规范要求。

表5 桥墩墩顶位移计算结果
(2)反应谱方法计算简单方便,但不能考虑非线性因素影响,更适用于弹性状态下的构件抗震验算;时程分析法计算精细,分析时应选用产生最不利弯矩的地震波,更适用于已进入塑性状态下的构件抗震验算,实际设计时两种计算结果要相互校核。
(3)反应谱计算结果表明,恒载和地震组合的最不利组合为最小轴力值控制验算,应当用组合后轴力的最小值进行首屈弯矩和等效屈服弯矩的计算。
