基于平行四边形柔性铰链的新型微量液体粘度测量方法*
2019-02-26薛卓阳赵美蓉乔沁雪郑叶龙
薛卓阳,赵美蓉,陈 曦,李 言,乔沁雪,郑叶龙
(天津大学精密测试技术及仪器国家重点实验室,天津 300072)
在石油化工,食品加工,医药制造等领域,了解液体的粘度特性具有重要意义。传统的粘度测量方法有旋转法,振动片法,毛细管法[1]等,但是这些传统的测量方法需要大量的被测液体,体积在mL量级。对于室温离子液体和像贻贝等的生物产生的有机分泌物,由于制备费用昂贵或者获取过程复杂,体积一般很少,利用传统的粘度测量方法,不容易进行粘度测量,因此急需提出一种准确高效的方法来测量微量液体的粘度。
近年来,随着MEMS技术的日益成熟,关于微量液体的粘度测量的研究也迅速发展。微量液体粘度测量方法主要分为石英晶体微天平测量法、电润湿法、表面力仪法和悬臂梁法等。石英晶体微天平(QCM)在进行液体测量时具有灵敏度高的优势。Doy等提出了利用石英晶体微天平来进行室温下离子液体的粘度密度乘积测量的方法,所需液体体积低至30μL[2],由于QCM的固有频率的检测限制,实验中粘度密度积不能大于121 mPa·s·g/cm3。Trols等通过建立浸润液体粘度和压力之间的关系,设计了基于电润湿和介电力的低成本粘度传感器[3],该装置的主要限制是压力场补偿时间和测量方法的灵敏度。对于粘度在50 mPa·s~100 mPa·s的液体,压力场的形成时间超过5 s,不能满足应用;根据标定结果,当粘度值为50 mPa·s时,测量误差达到36%。表面力仪是微纳领域最重要的研究成果之一,并且被广泛应用于液体特性的研究。因为凝聚相的粘弹流体特性会随着混合比的变化,从剪切稀化转化为剪切增稠,所以表面力仪可以用来测量复杂凝聚物的粘度[4]。
原子力显微镜微悬臂梁(AFM)在微量液体粘度和密度测量上被广泛应用。振动的悬臂梁具有灵敏度高的优点,并且可以将所需液体体积缩小至微升量级。主要的理论基础是浸润在液体中的被夹紧的悬臂梁在谐振力的作用下的运动方程[5-9]。McLoughlin等利用电磁力驱动的悬臂梁测量了水-乙醇溶液的粘度,测量误差低于5%,同时样品体积为微升量级[5]。Youssry等在简化悬臂梁理论的基础上建立了梁的偏转表达式[6],测量了液体的粘度和密度,并且不需要获取悬臂梁的一阶谐振峰。当粘度值从1.67mPa.s增加到111 mPa·s,粘度的测量误差从13.2%增加到46.9%。Cerimovic等测量了粘度范围在0.18 mPa·s~81.5 mPa·s的甘油水溶液[7]。Eris等利用微悬臂梁的频率响应测量了氮气的在临界条件下的粘度密度乘积[8],密度和粘度的均方差分别是2.5%和5.2%。Benjamin A Bircher等考虑了谐振模态中更高阶的扭转模态,利用微纳结构的谐振器测量液体粘度密度乘积,来监控聚合物的反应过程,所需的液体体积为5 μL[9]。在反应过程中,粘度的变化范围为1 mPa·s~20 mPa·s。测量原理基本一致,举例说明悬臂梁法在进行粘度测量时范围较小的原因。在参考文献[5]中,使用受迫振动的幅值频率曲线拟合得到粘度和密度,当被测的粘度增大时,幅频曲线的最高点会越来越切近横坐标,而曲线拟合的所带来的误差将被放大,类似病态矩阵的原理,曲线拟合轻微的误差将会给计算粘度带来非常大的误差,对大粘度液体,此种拟合方法不再使用。
综上所述,前人的研究不断完善微量液体粘度测量的相关研究,同时悬臂梁法也被广泛应用。目前,微量液体的粘度测量法仅能测量粘度值在0~150 mPa·s范围内的液体。为了解决测量范围有限的问题,本文采用了基于平行四边形柔性铰链的微量液体粘度测量方法。将刚性杆的基底部分与平行四边形柔性铰链结合,使得刚性杆的探针部分在液体中运动时主要受剪切力,达到测量微量液体粘度,并扩大量程的目的。

图1 系统整体构成图
1 测量原理以及实验系统搭建
1.1 系统搭建
本系统包括刚性杆、平行四边形柔性铰链(下文简称铰链)、激光干涉仪、反光镜、容器和微米级位移平台等。搭建的系统装置如图1所示。其中刚性杆分为基底和探针两部分,结构与大尺寸的AFM结构相似,如图2所示;平行四边形柔性铰链[10-11]具有较高的灵敏度,能够减小纵向和侧向位移,力值和变形呈较好的线性关系,刚度k=15 N/m;激光干涉仪型号为RENISHAW RLE10;微米级位移台型号为Zolix KSAV1010-ZF;设计的容器是一个高2 mm,直径3 mm的圆柱形凹槽。
刚性杆的基底部分粘贴在铰链的底端,探针部分在微米级位移台的控制下插入到被测液体中,在由瞬态力发生装置产生的脉冲信号的激励下,铰链做一维简谐振动,带动探针在被测液体中做剪切运动。
采用瞬态力发生装置,在铰链上施加相同的力,改变系统的初始状态,使每次测量时,系统具有相同的初始位移和初始速度。系统的初始状态相同,有利于准确地计算阻尼因数。利用激光干涉仪采集铰链的位移信号,并根据位移信号的衰减速度计算出与液体粘度正相关的系统的阻尼因数。
本文中使用的刚性杆结构和悬臂梁法中使用的悬臂梁结构形状相同。前人使用的悬臂梁法的主要原理是在外力的驱动下,使悬臂梁在浸润液体中的做纵向运动,如图2中的虚线箭头所示。本文利用平行四边形柔性铰链带动刚性杆的探针部分在液体中做横向剪切运动,如图2中的实线箭头所示,探针在做剪切运动时,所受到的阻力相对其他悬臂梁方法更小,衰减会更慢,则能够测量更大的粘度范围。
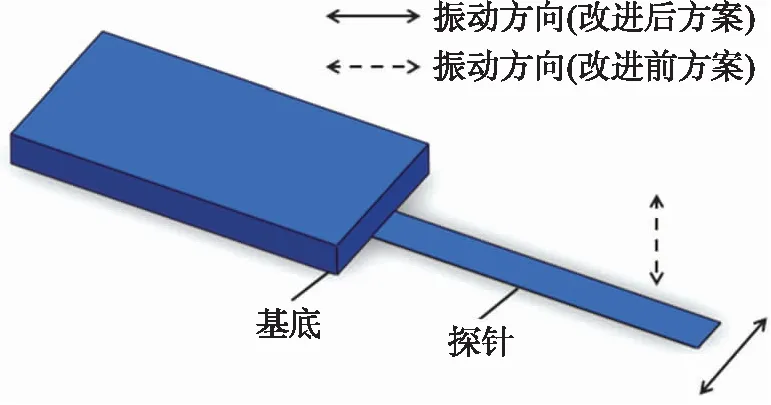
图2 刚性杆结构以及振动方向示意图
1.2 测量原理
平行四边形柔性铰链在脉冲激励的作用下,其振动可视为一维的阻尼振动[10],动力方程表示为:
(1)
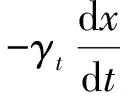
那么,阻尼振动的运动方程为:
(2)

βt也可以表达为βt=β+β0。其中,β表示由液体的粘性力造成的阻尼因数,β0表示由铰链的内摩擦造成的阻尼因数,可以认为是一个常数。
当薄而平的探针在牛顿流体中做剪切运动时,流体负荷引起的力阻抗Z等于作用在探针表面的粘性力与探针速度比值[12]:
(3)
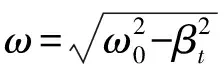
力阻抗Z也可以表达为:
Z=Rz+jXz
(4)
式中:Rz和Xz分别代表力阻和力抗。
探针在液体中做剪切运动过程中受到的力阻Rz等于系统在做阻尼振动时受到的液体产生的阻尼系数γ[12],那么阻尼因数β可以表示为:
(5)
根据式(5)得到液体粘度η的表达式如下:
(6)


图3 探针在液体中产生的润湿现象
在控制探针插入液体一定深度时,探针表面和液体接触的界面会出现润湿现象,如图3所示。润湿现象是由液体的表面张力造成的,由于液体分子间引力和分子间结构的差异造成了表面张力不同,不同液体在探针表面会形成不同的吸附高度的润湿现象[13-14]。在粘度测量过程中需要消除润湿现象对测量结果的影响。由式(5)可以得到,液体的阻尼因数β和探针与液体的接触面积S成正比,则由于润湿现象,在不同吸附高度下会存在不同的阻尼因数。本文采用差分法,将探针从某一插入深度到另一插入深度的阻尼因数的变化量作为式(6)中的阻尼因数计算代入值。
2 实验方法及结果
2.1 实验方法
本文使用的基于平行四边形柔性铰链的粘度测量方法包括实验台预调整阶段、激励与位移响应阶段、阻尼因数拟合阶段、系统标定阶段和粘度计算阶段五部分。
①实验台预调整阶段。调整容器位置固定装置的水平位置,使得容器的中心线与探针中线延长线大致在一条直线上。从而通过调整微米级位移平台的高度改变容器的上端面与刚性杆的探针底端之间的距离来达到更换待测液体的目的。
②激励与位移响应阶段。通过调整微米级位移平台的向下运动使探针插入液体一定深度,通过瞬态力发生装置给铰链施加一个脉冲激励,铰链带动反光镜产生位移响应,通过激光干涉仪得到位移变化的数据集。
③阻尼因数拟合阶段。根据激光干涉仪采集到的反光镜处的位移随时间变化的信号,利用MATLAB程序获取位移时间信号的上包络点,对包络点进行对数操作,画出上包络点进行对数变换之后的位移随时间变化的散点图,进行基于最小二乘线法的线性拟合,得到的直线的斜率即为此时探针在液体中的阻尼因数。
④系统标定阶段。控制微米级位移平台以固定步长位移值下降,将探针浸润到液体的不同深度中,重复步骤②~步骤③,得到不同浸润深度下探针在液体中的阻尼因数。对不同粘度的液体,取相同浸润深度差对应的总阻尼因数之差作为阻尼因数的代入计算值,可以表示为β=βt1-βt2,以消除润湿现象的影响。由式(6)可得,使用标准粘度液可以完成微量液体粘度测量装置的标定过程:在标准粘度液的粘度和密度已知的情况下,根据测量得到的阻尼因数计算代入值,计算出比例系数c。
⑤粘度测量阶段。按照步骤④中计算液体的阻尼因数代入值的方法,计算粘度未知的液体的阻尼因数代入值,结合标定得到的比例系数c,计算出待测液体的粘度。
2.2 实验结果
2.2.1 标定实验
使用五种不同粘度的标准粘度液体进行系统标定,分别编号为A,B,C,D,E,在标定实验之前,先测量五种不同液体对应的粘度和密度,相应的参数信息见表1。其中粘度密度乘积由AND SV10型粘度计测量得到,重复性精度为1%,密度由JA3003J型精密天平测量得到。
首先测量探针在不同深度下做剪切运动时,系统的总阻尼因数。设置微米级位移平台以0.25 mm为步长,使探针浸润到液体中的深度从0.25 mm增加到1.00 mm。在四种不同的浸润深度中,总阻尼因数随着浸润深度的增加呈线性变化。接着建立液体粘度和系统阻尼因数的关系。阻尼因数代入计算值取浸润深度为0.75 mm与0.25 mm处所处的阻尼因数之差,差分后的测量结果见表1最后一列。通过表1可以看出,液体粘度越大,对应的阻尼因数的代入值越大。根据线性拟合,得到粘度和阻尼因数之间的关系,如图4所示。
由于五种被测液体的粘度分散性较大,将图4的横轴绘制成粘度与密度乘积的二次方根,纵轴绘制为阻尼因数代入计算的差分值。验证了上述粘度测量模型中,粘度与阻尼因数的平方成正比。根据表1中的数据完成系统的标定,得到比例系数c=0.002 48,液体的粘度测量范围为10 mPa·s~750 mPa·s。
2.2.2 验证实验
为了验证基于平行四边形柔性铰链的粘度测量方法的测量精度,利用设计的微量液体粘度测量装置,依次对不同浓度的甘油水溶液进行粘度测量,根据标定实验中得到的比例系数c,计算出待测甘油水溶液的粘度,本实验方法的粘度测量结果和用粘度计AND SV10的粘度测量结果对比见表2。为了说明测量的可靠性,也将验证实验中用到的数据点表示在图4中。粘度测量的相对误差平均为5.8%,最大为8.3%。

表1 标定实验中的液体的参数信息以及阻尼因数

表2 验证实验的结果记录
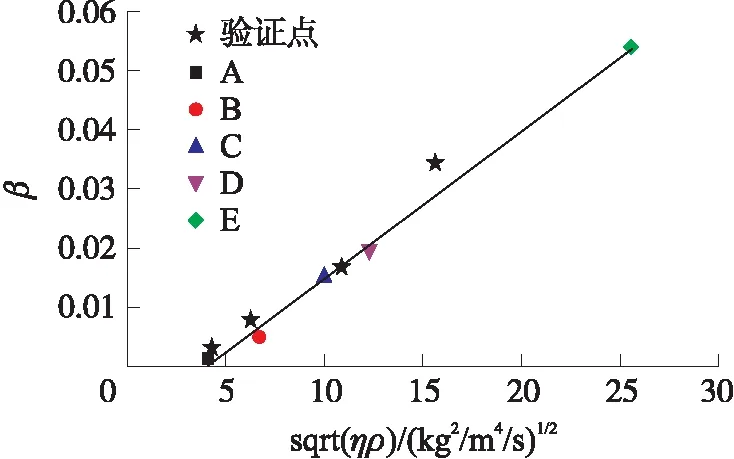
图4 粘度密度与阻尼因数的关系
2.3 误差分析
在实验过程中,保持环境中温度基本不变,忽略环境变化造成的误差,认为粘度的测量误差来自密度ρ的测量误差以及数据的拟合和计算过程。
比例系数c的拟合值与系统质量m,接触面积S,以及系统的振动频率f有关。在实验过程中,系统质量m保持不变;由差分法得到的接触面积S为定值;系统的振动频率f可以通过对位移时间信号进行傅里叶变换得到,计算五种粘度的液体的位移时间信号对应的系统振动频率,发现其值均为12.94 Hz。因此,拟合比例系数c时引入的误差可以忽略不计。
阻尼因数代入计算值β=βt1-βt2的计算误差等于两次阻尼因数的拟合误差之和,在2.1实验方法中的阻尼因数拟合阶段的最小二乘线性拟合过程中,相关系数R2分布在0.990~0.996之间,曲线拟合程度较好,认为阻尼因数代入计算值引入的误差可以忽略。
密度ρ的测量误差来源于液体的质量m1和液体体积v1。用移液枪进行微量液体体积的测量转移,查阅资料可得,移液枪的最大容许误差是±3%,天平JA3003J的重复性误差为±0.001 g,待测液体的体积约为0.014 g,根据间接测量的误差传递公式[15]可得:
(7)
密度ρ的测量误差为质量测量误差和体积测量误差之和,约为10%。由以上分析可得,粘度测量的主要误差来源为密度ρ的测量误差,误差的范围与验证实验测量结果基本相吻合。
3 结论
本文设计了一种基于平行四边形柔性铰链的大量程新型粘度测量方法。该方法需要的待测液体的体积为15 μL,测量范围是10 mPa·s~750 mPa·s。实验装置将刚性杆的基底部分粘贴在平行四边形柔性铰链的底端,在瞬态力的作用下,两者做一维的阻尼运动,刚性杆的探针部分在液体中剪切运动,测量计算阻尼因数,实现粘度测量,并进行了实验验证,得到粘度测量的相对误差平均为5.8%。未来的工作将放在进一步减小密度的测量误差上,争取实现密度和粘度的同时测量。
