双层矩形微板谐振器件中热弹性阻尼机理研究*
2019-02-26左万里黄家瀚
左万里,黄家瀚
(宁波大学机械工程与力学学院,浙江 宁波 315211)
微电子机械系统(MEMS)在科学和工程领域有着广泛的应用[1-2],如微传感器与微谐振器等。对于谐振器,品质因数(Q)是一重要参数,其关系到器件的测量精度。品质因数越高,器件振动时的能量损失越小。在过去的几十年中,为了制造高精度即低能量损失的谐振器,众多学者研究了多种不同的阻尼机理。在这些阻尼机理中又可分为外部阻尼和内部阻尼。外部阻尼如空气阻尼[3]和支撑阻尼[4]可以通过合理的设计与优化运行环境来降低和消除。但是内部阻尼,如热弹性阻尼很难像外部阻尼那样消除。因此,热弹性阻尼长期以来一直是研究热点。
上个世纪三十年代Zener[5-6]针对均质、各向同性的板簧首次提出了热弹性阻尼这一概念。当板簧做横向周期振动时,板簧上下部分会周期性的被压缩与拉伸,压缩部分温度会上升,拉伸部分温度会降低,从而产生了一个温度梯度。这一温度梯度又会产生不可逆热流,即带来了熵增,这一能量损失则被称为热弹性阻尼。其模型表达式定义如下:
(1)
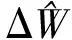
在过去的数十年间,许多学者研究了均质结构中的热弹性阻尼。Lifshitz和Roukes[7]优化了Zener的模型。Li[8]给出了out-of-plane振动时均质矩形板和圆板中的热弹性阻尼模型。Li模型与LR模型之间的关系如下
(2)
式中:ν为泊松比。
近年来,随着MEMS技术的进步,层叠微结构在谐振器中得到了应用[9]。层叠微结构通常采用化学汽相淀积,真空喷镀淀积等工艺制造,与宏观复合材料有较大的区别。在层叠微结构器件中,每一层材料都是各向同性的,层层之间没有间隙,界面处无熵增。层叠结构中的热弹性阻尼理论最早由Bishop和 Kinra[10-11]提出——热弹性阻尼为单位弧度内,所有层中能量损失之和与最大储存能之和的比值。但Bishop和Kinra理论框架中含有待定的未知量,不能方便地、直接地用于计算谐振器件中的热弹性阻尼。基于Bishop和Kinra的理论框架,Vengallatore[12]研究了对称三层梁中的热阻尼,Vengallatore研究团队[13-14]给出了双层微梁中热弹性阻尼解析模型。本文基于Bishop和Kinra理论框架,建立了横向振动时,双层矩形板微谐振器中热弹性阻尼模型。
1 方法
在Bishop和Kinra[10-11]的理论框架下,双层板中的热弹性阻尼定义如下
(3)
式中:下标( )1表示基板,下标( )2表示镀层。
(4)
式中:Vm是第m层板的体积,σij,m和εij,m分别为第m层板内的应力张量和应变张量。
(5)
式中:σkk,m是第m层板中合应力,εT,m是第m层中热应变,Im( )表示取虚部。
2 应变和应力场

(6)
假定变化的温度场为ϑ=T-T0,其中T0为初始温度,在均质各向同性材料中,机械应变和热应变可表示为
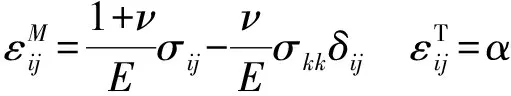
(7)
式中:合应力σkk如下所示
σkk=σxx+σyy+σzz
(8)
克罗内克函数δij可表示为
(9)
则总的应变场为
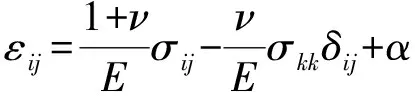
(10)
由式(10)可以推导出应力场为
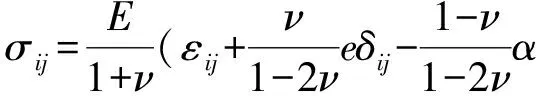
(11)
式中:体应变e为
e=εxx+εyy+εzz
(12)
当微板进行小变形振动时,平面内的应变分量εij与位移向量ui之间的关系如下[14]
(13)
一般记平面内位移为ux=u(x,y,z),uy=v(x,y,z),横向位移为w(x,y,z)。
假设板在角频率为ω的激振力作用下进行横向振动,则板的横向变形可记为[8,14]
w(x,y,z,t)=w0(x,y)eiωt
(14)
平面内位移为
(15)
(16)
由于波动温度场ϑ是由振动而产生的,根据热弹性效应,则有
ϑ(x,y,z,t)=ϑ0(x,y,z)eiωt
(17)
在直角坐标系下,坐标原点设定在双层板底面,如图1所示。z1为基板厚度,z2为基板与镀层总厚度。由式(10)可得到双层板中应变分量的本构方程;同时由式(13)、式(15)和式(16)可得双层板中应变场与位移函数之间的关系式如下
m=1,2
(18)
式中:Em、νm、αm分别是第m层中材料的杨氏模量、泊松系数、热膨胀系数,z0为中性面距坐标原点的距离。2008年,Zhang和Zhou[16]给出了非均质板内中性面近似计算方法,运用这一方法,可得双层板中性面为
(19)

图1 双层板结构示意图及其坐标系
双层板中的应力分量的本构方程为[8,15]
m=1,2
(20)
3 双层微板中热弹性阻尼
3.1 双层矩形板中储存的最大弹性能
将式(18)和式(20)代入式(4),可得双层板内,每一层所储存的最大弹性能为
(21)
(22)
式中:
(23)
A为板在(x,y)平面内的面积。
3.2 损失的耗散能
当薄板横向振动时,z向温度梯度要远远大于x向和y向的温度梯度。对于双层板,含有内部热源项时的一维热传导方程可记为[11,17]
(24)
式中:内部热源项
(25)
当双层板为外表面绝热,且内部界面无热量损失时,其对应热边界条件为
(26)
由积分变换[18]可解得双层板的稳态温度场为
(27)
式中:
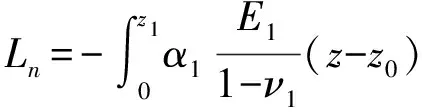
(28)
(29)
式中:φmn(z),βn为下列问题的特征函数和特征值
(30)
则特征函数为
(31)
(32)
式中:
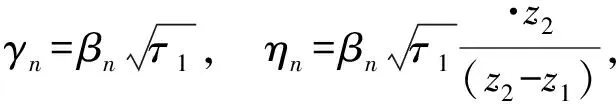
而βn是下列超越方程的根:
(33)
将式(7)、式(8)和式(27)代入式(5)得每一层损失的能量为
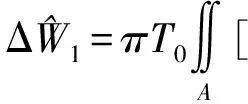
(34)
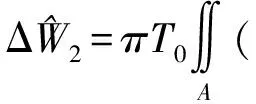
(35)
式中:
(36)
(37)
(38)

(39)
则将式(21)、式(22)、式(34)和式(35)代入式(3)可得双层矩形板中的热弹性阻尼如式(40)所示
(40)
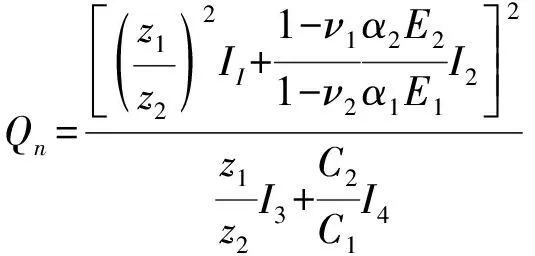
(41)

(42)
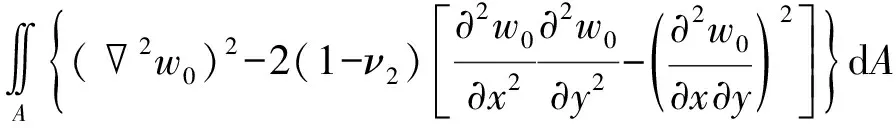
(43)
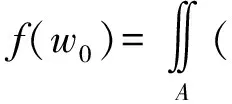
(44)
(45)
3.3 周边固定板
根据板壳理论[19],高斯曲率G(w)在直角坐标系记为
(46)
当双层板为周边固定时(Fully clamped),对高斯曲率进行积分后,所得结果都为零,即
(47)
将式(47)代入式(42)和式(43)后,式(40)中板的振型项可以化减,得双层周边固定板中热弹性阻尼模型为式(48):
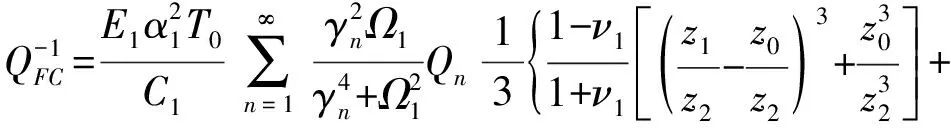
(48)
4 结果和讨论
利用已建模型分别讨论周边固定双层矩形微板中,镀层的体积比Vf、板的几何尺寸等对热弹性阻尼的影响。其中Vf为镀层厚度与双层板总厚度的比值,即
Vf=(z2-z1)/z2
(49)
300 K时材料的力学参数如表1所示。

表1 300 K时材料特性
4.1 当前模型理论结果
图2为在硅板上镀有不同材料时,热弹性阻尼随频率的变化关系。为了与均质单层硅板进行比较,图中也给出了均质微板中热弹性阻尼模型[8]计算结果。由图可知,当镀层材料的Zener模量大于硅的Zener模量时,最大热弹性阻尼会增加;而镀层材料的Zener模量小于硅的Zener模量时,最大热弹性阻尼会降低。

图2 不同镀层时频率对热弹性阻尼的影响
图3为在SiO2基板上镀有金属Au后,热弹性阻尼随频率的变化关系。图中也给出了均质SiO2板中的热弹性阻尼[8]。从图中可以看出,Au/SiO2热弹性阻尼谱中会出现两个峰。比较均质板的热弹性阻尼频谱曲线可知,双层板中的第一个峰主要由SiO2基板作用而产生。同时由式(1)中临界频率ω=π2k/h2C也可知,双层板中第一个峰所对应的临界频率为均质SiO2板的临界频率,而第二个峰的临界频率为均质Au板的临界频率。由于Au的Zener模量远远大于SiO2的Zener模量,虽然Au镀层板厚度只有细微的增加时,但是热弹性阻尼却会快速增大。
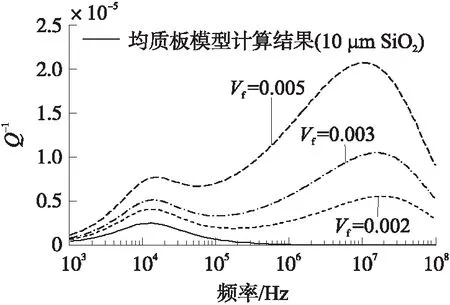
图3 Au/SiO2(z2=10 μm)双层板中金属层体积比对热弹性阻尼的影响
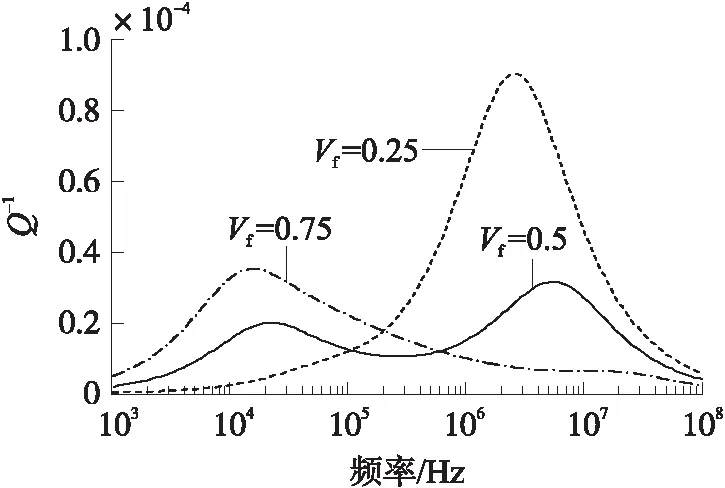
图4 SiO2/Si(z2=10 μm)双层板中淀积层体积比对热弹性阻尼的影响
图4为SiO2/Si中镀层SiO2的体积比对热弹性阻尼的影响。当Vf=0.25时,Si层中热弹性阻尼占主导作用;当Vf=0.75时,SiO2层中热弹性阻尼起主导作用。上述两种情况下,热弹性阻尼频谱曲线仅有一个波峰。仅在Vf=0.5时,热弹性阻尼频谱曲线会出现两个波峰。由此可知,双层板中的热弹性并非两块均质板热弹性阻尼的简单叠加。
4.2 与FEM结果的比较
运用所得模型计算双层矩形板中热弹性阻尼并与FEM(ANSYS)结果进行比较。在ANSYS中,运用结构-热力学简谐分析去计算板中的热弹性阻尼。本文采用了三维20节点的Solid226单元去划分每一层板。
图5为Si3N4/Si中ANSYS所得热弹性阻尼的数值解与当前模型所得解析解的比较。双层微板的总厚度z2=10 μm,长宽和宽度为a=b=500 μm。由图可知,ANSYS数值模型所得结果与当前解析模型所得结果具有很好的拟合度。不同体积比条件下,热弹性阻尼频谱曲线都仅有一个波峰;仅当Vf=0.25时,双层微板具有较宽的阻尼频谱曲线。
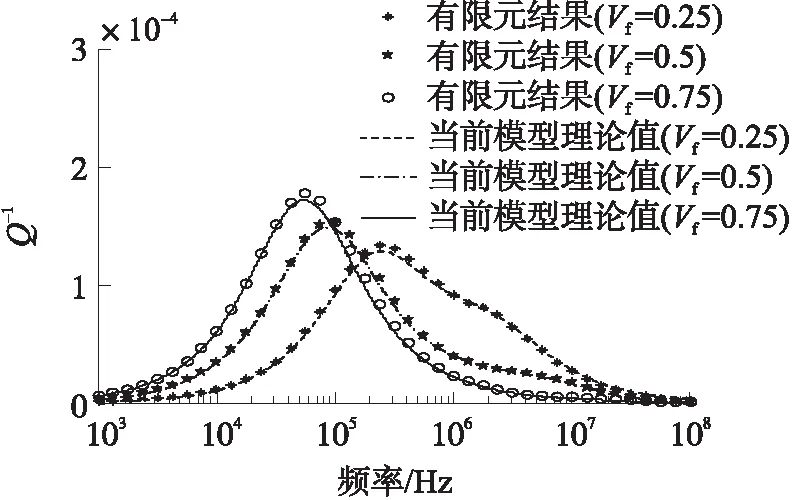
图5 Si3N4/Si中热弹性阻尼ANSYS结果与理论值的比较
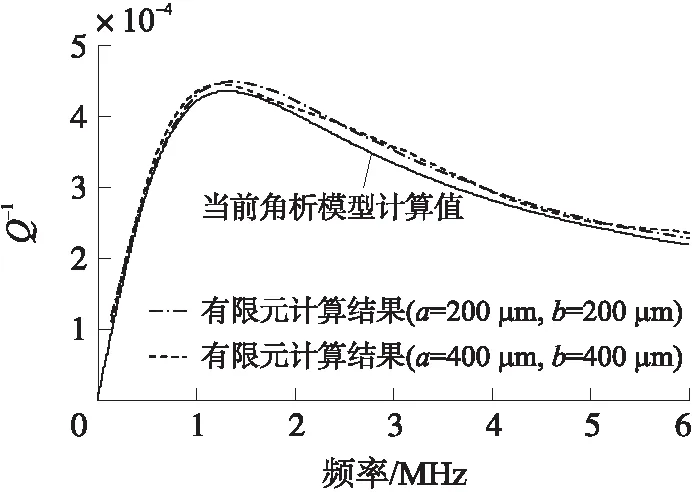
图6 Ag/Si中热弹性阻尼ANSYS结果与理论值的比较
由式(48)可知,双层微板谐振器中的热弹性阻尼仅与板的厚度有关,而与板的长度和宽度无关。图6为矩形板在不同长宽比(b/a)时的热弹性阻尼。其中双层板的总厚度固定(z2=10 μm),体积比Vf=0.1。由图可知,虽然板的长度和宽度都增加了一倍,ASNSY所结果却无明显变化,且与理论模型所得解析解具有很好的拟合度。
5 结论
本文针对双层矩形板结构微谐振器,基于Bishop和Kinra理论方法,建立了周边固定条件下,热弹性阻尼解析模型。主要结论如下:①当镀层材料的Zener模量大于基板材料的Zener模量时,最大热弹性阻尼会增加;而镀层材料的Zener模量小于基板材料的Zener模量时,最大热弹性阻尼会降低。②双层板中的热弹性并非两块均质板热弹性阻尼的简单叠加。双层板热弹性阻尼频谱曲线的波峰特性,由材料的Zener模量和临界频率所决定。③对于双层板谐振器,板的厚度对热弹性阻尼的影响较大,而板的形状,长宽的影响可以忽略。
