基于卡尔曼滤波的四轴飞行器成像、惯性和高度组合导航*
2019-02-26莫申童
邹 强,付 超,莫申童
(1.天津大学微电子学院,天津 300072;2.天津市物联网国际联合研究中心,天津 300072;3.天津市成像与感知微电子技术重点实验室,天津 300072;4.天津大学青岛海洋技术研究院,山东 青岛 300072)
由于惯性导航系统INS(Inertial Navigation System)陀螺仪、加速度计等传感器的自身测量误差,还会受到机体震动、温度等多方面影响,以致测量数据不精准[1]。同时,当四轴飞行器在城市环境或室内环境下,GPS信号受到干扰甚至丢失,无法利用GPS实现精准定位,因此需要一种全新的室内导航技术,实现室内精准导航[2]。
现有的研究已经表明,将一组互补传感器提供的数据进行融合是一种能够完全估计无人机状态参数以及感知周围环境的适用方法[3-4]。Kelly J等提出了组合立体视觉测程法和惯性测量的无人机导航系统。无人机的位置和姿态由两个传感器给出的运动估计经扩展卡尔曼滤波器融合得到,由导航系统提供的信息经离线分析,以评估点对点导航任务性能[5]。Croke P等给出了应用于飞行器的视觉和惯性传感器系统相结合的实例。在该实例中,视觉和惯性传感器系统用于对小型直升机进行实时控制。地面高度信息和自运动引起的光流由一对下视摄像机提供。互补滤波器用于融合从惯性和视觉传感器得到的速度信息[6]。文献[7]中发现关于无人机视觉定位的有趣结果。Blosch等利用单目视觉系统实现实时定位与地图建模SLAM(Simultaneous Localization And Mapping)算法。试验结果表明,该算法能对室内飞行的四旋翼无人机进行精准的定位。文献[8]提出了一种视觉伺服系统,通过四个圆形标志,对四轴飞行器进行位置控制。Ahrens S等通过一组跟踪特征对四轴飞行器自身进行估计,能够实现环境感知和躲避障碍物[9]。孔天恒等利用二维激光雷达和惯性导航系统构成微小型无人机MAV(Micro Aerial Vehicle)室内组合导航方案,采用基于扩展卡尔曼滤波EKF(Extended Kalman Filter)的D&C同步定位与构图技术(SLAM)实现定位和构图[10]。
本文提出一种基于卡尔曼滤波的四轴飞行器成像、惯性与高度组合导航,使四轴飞行器实现自主起飞、相对定位、导航和着陆。根据人造地面标志,通过相对姿态估计算法来确定飞行器的位置,利用光流算法来调节飞行器的运动速度。实验结果表明,基于互补滤波的四轴飞行器成像、惯性与高度组合导航能够对飞行器平移运动状态进行精确估计,对飞行器的三维轨迹进行有效重建。
1 摄像机模型与标定
机载视觉传感器的配备,使四轴飞行器获取周围环境信息以及自身信息的原始方法得以发展。然而,在使用视觉传感器之前,必须建立数学模型,用于描述三维空间点与二维图像点之间的对应关系。
摄像机模型如图1所示,其中OXcYcZc为摄像机坐标系,(xcam,ycam)为图像坐标系,(x,y)为图像像素坐标系,物体空间点X在摄像机坐标系下被映射到图像坐标系x的转换关系为:
(1)
令
(2)
式中:(px,py)为图像坐标系中的主点坐标,K为摄像机标定矩阵,由摄像机的投影矩阵P的RQ分解导出,而P由给定足够多的三维点X与二维图像x的对应点确定。
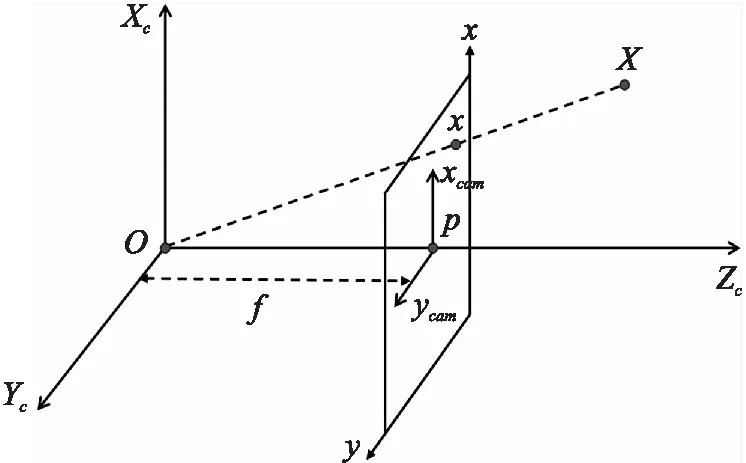
图1 摄像机模型

图2 氧化铝标定板
原则上,任意带有适当特征的物体都可以作为标定物,但最符合实际的选择是规则图案,如棋盘。
棋盘特征点的测量误差和图像中相对应角点的提取误差与相机标定的误差成正相关性[11],且棋盘格尺寸较小的靶标,相机的标定误差较小[12]。本文建立了精度为0.01 mm的180 mm×180 mm棋盘格,其中包含相互交替且尺寸为15 mm×15 mm的黑白方格,如图2所示。
通过MATLAB摄像机标定工具箱可以精准的计算出摄像机的内外参数,为了获得较高的精度,拍摄了20幅不同方位和位置的棋盘图像,如图3所示。图4展示了标定工具的图像序列。

图3 摄像机与靶标之间关系

图4 MATLAB GUI中摄像机标定工具箱中的棋盘图案
利用工具箱计算出的OV7275摄像机的参数矩阵K为

(3)
若要根据图像信息得出飞行器在世界坐标系下的位置和姿态,还需要建立机体坐标系到世界坐标系的关系,世界坐标系与摄像机坐标系之间可通过一次旋转和一次平移联系起来。
(4)
世界坐标系与机体坐标系之间的转换矩阵R为:
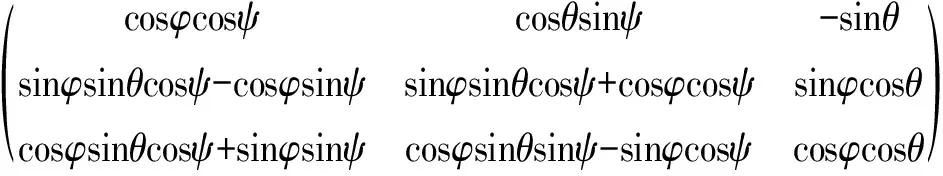
(5)
式中:φ为横滚角、θ为俯仰角、ψ为偏航角。
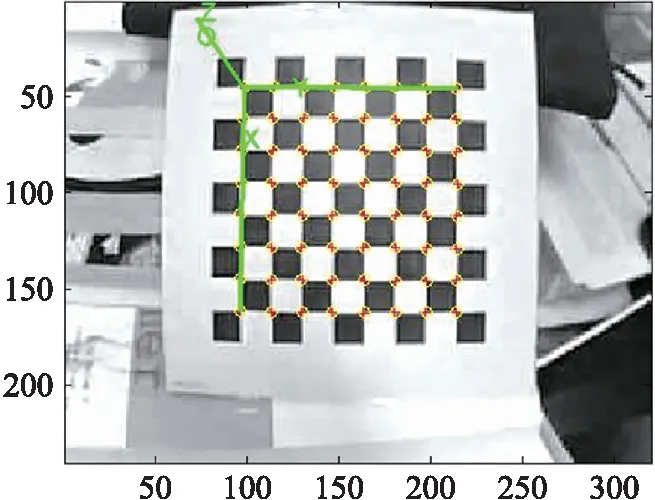
图5 序号2图像外参数:平移矩阵和转换矩阵的计算
以图像5为实例,测得平移矩阵T为:
T=[-53.569 795 -46.582 296 244.833 651]
(6)
转换矩阵R为:

(7)
通过上述原理和方法,求出摄像机相对于标志物的位置和姿态后,四轴飞行器在空中相对于着陆标志的位置和姿态也就唯一确定了。
2 着陆标志设计
实现四轴飞行器三维位置控制需要着陆平台或地面人工标志,本文设计了一种着陆标志如图7所示。
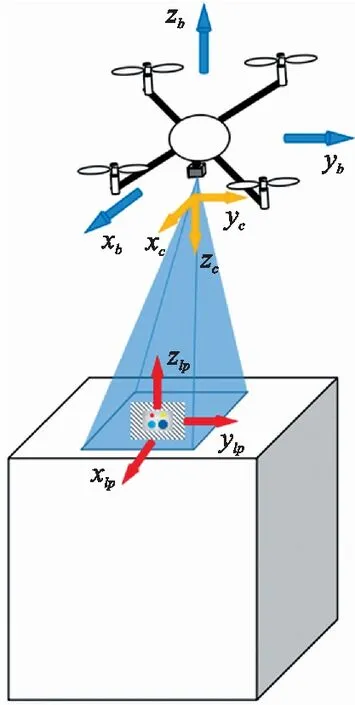
图6 基于视觉的位置稳定原理图
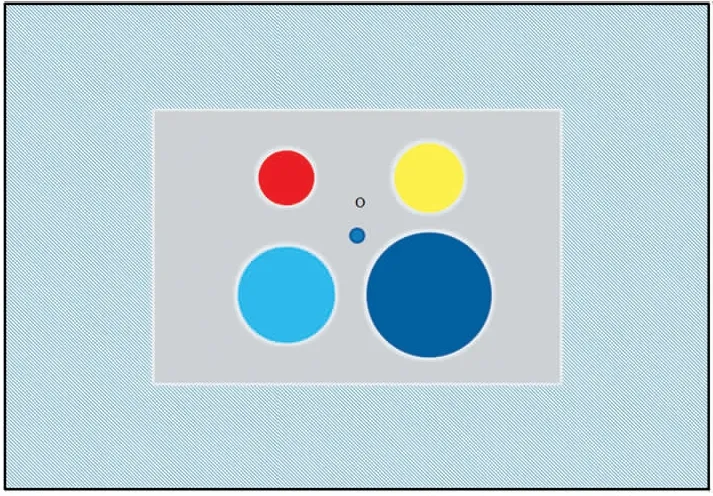
图7 四个圆环着陆标志
对于四轴飞行器在空中悬停的每一个时刻,利用已知四个圆圆心位置的先验知识,可以计算出单应性矩阵H。利用该估计转换矩阵和基于文献[13]方法离线辨识校准的摄像机内参数矩阵,可以计算出摄像机的外参数,得到飞行器相对于着陆平台的位置(x,y,z)。识别流程如下:
Step 1 Hough圆形检测 利用OpenCV Hough函数可以检测到图像中的每一个圆,根据圆的半径大小进行分类,可以实现对着陆平台坐标的正确辨识。第一个圆对应右下圆,将左下圆作为列表中的第二个圆,然后依据半径大小确定为右上圆,最终左上圆被辨识为半径较大的圆。图8显示了从摄像机中观测到的着陆平台图像,四个圆环根据其半径大小用紫色圆环凸显出来。
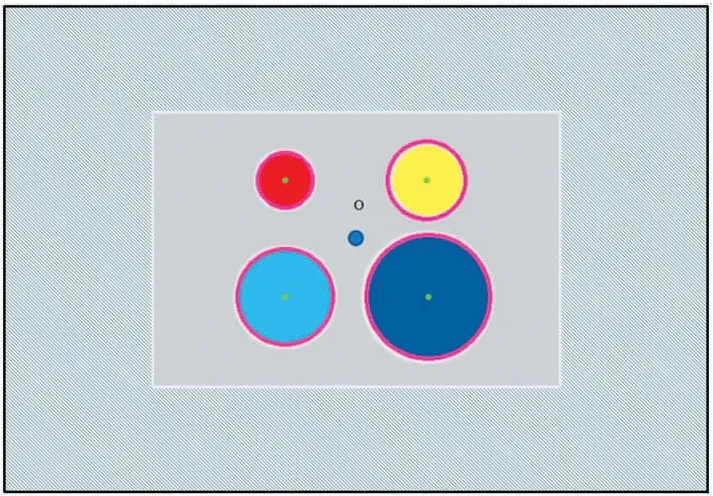
图8 单应性图像估计:四个圆环的检测和颜色识别
Step 2 圆环排序 必须忽略着陆平台圆环的错误检测,否则将提供一个错误的位置估计。因此,总平台检测到的四个圆环圆心的颜色必须被确认。图8显示着陆平台四个颜色不同的圆环。四个圆环按半径从大到小依次为深蓝色、浅蓝色、红色、黄色。
Step 3 颜色确认 图9为四个圆环圆心颜色识别流程,通过摄像头采集到着陆标志的图像,利用Hough变换检测到圆,并确定圆心坐标,将彩色图像由RGB模型转换为HSV模型,设定上述颜色的阈值,在此设定阈值内,将图像二值化,再次检测圆心坐标的颜色是否为白色,识别出颜色。
每次四个圆环的检测,首先要经过以上两项约束确认,保证一个好的平面单应性被估计,目的是获得较好的摄像机外参数计算。
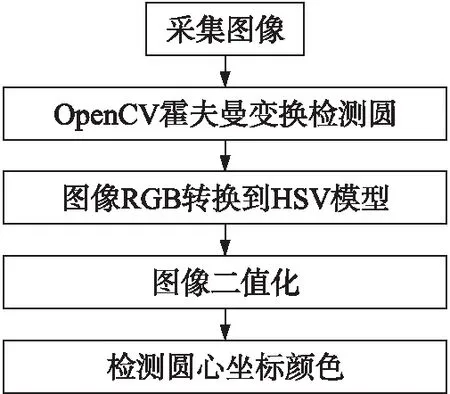
图9 四个圆环圆心颜色识别
3 视觉、惯性与高度数据融合
3.1 成像系统相对高度估计
利用文献[14]提出的方法,摄像机固定在四轴飞行器上,因此相对高度的估计就是计算着陆标志在摄像机坐标系下的位置坐标。图10为相对高度估计的原理图,由相似三角形定理求出高度h的值。
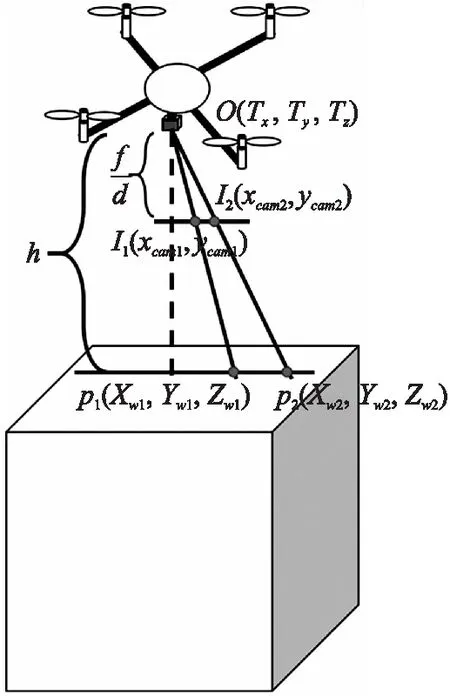
图10 高度、焦距和标志特征点位置的几何对应关系
图中f/d为摄像机焦距的长度,由摄像机标定得出。P1,P2是世界坐标系下的两个特征点,I1,I2是其在图像坐标系下的映射点,由相似三角形定理,可以得出下式:
(8)
计算出任意两个特征点P1,P2的坐标以及它们映射点的像素坐标,就可以测量出|P1P2|的物理距离,并得出|I1I2|的像素距离,从而得到相对高度h。
3.2 Lucas-Kanade金字塔光流法估计位移速度
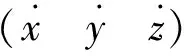
假设摄像机相对于着陆标志相对运动,在惯性坐标系下的速度和自转速度分别表示为(VxVyVz)和(wxwywz)。为了准确估计四轴飞行器的伪速度,在着陆平台定义一个跟踪区域,该区域中心与着陆平台中心重合。通过OpenCV函数来检测着陆标志上最具代表性的特征。本文选择4个圆环的圆周为跟踪特征。在图11整个图像上执行基于OpenCV光流算法的跟踪过程,并测量被跟踪特征的位移。

图11 光流估计相对平移速度
稠密光流对图像中每个像素点都进行计算,运算时间较长,考虑到四轴飞行器的快速运动要求导航系统具有实时性,因此本文采用稀疏光流对图像中的模式运动进行运算。
圆周光流平均值可以表示成如下运动过程:
OFx=VOFx+PxVOFz+IOFx
OFy=VOFx+PyVOFz+IOFy
(9)
利用文献[15]对转动光流进行补偿,并推导伪速度(VOFxVOFyVOFz)。由于摄像机安装并固定在四轴飞行器上没有自由度,因此,推导的伪速度取决于四轴飞行器的运动。可以写成:
(10)
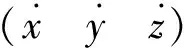
当四轴飞行器做等高飞行时,通过式(10),本文提出的光流视觉系统就可以按照一定的比例因子实现对四轴飞行器的速度估计,从而来控制飞行器的平移速度。
3.3 卡尔曼滤波器融合数据
为了能够精确估计四轴飞行器的位置和速度,本文通过卡尔曼滤波算法将视觉、惯性和高度数据进行融合。
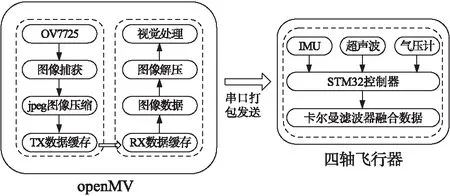
图12 视觉、惯性与高度数据融合过程
状态更新向量定义为
(11)
观测更新向量定义为
Z[k]=[xVOxa,imuyVOya,imuzVOza,imuzas]T
(12)
式中:(xVOyVOzVO)为由视觉传感器得到的飞行器位置测量值;(xa,imuya,imuza,imu)为惯性测量单元测量的加速度值;zas为超声波传感器提供的测量值。滤波器融合了zVO与zas来得到更准确的飞行器高度估计值。
根据式
(13)
计算C′矩阵。
根据式
(14)
(15)
得到此时的滤波增益矩阵H(k)。
根据式
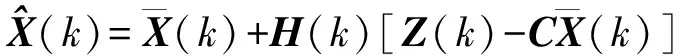
(16)
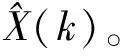
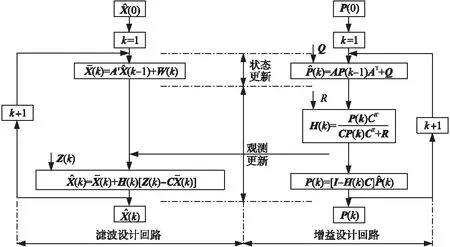
图13 卡尔曼滤波算法预测更新流程图
根据式
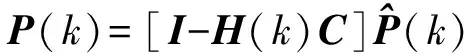
(17)
计算下一时刻的协方差P(k),当系统进入k+1状态时,P(k)就是式(14)的P(k-1),这样卡尔曼滤波算法就可以自回归的运算下去。
4 实验与结果
4.1 实验平台概述
本文组合导航实验平台如图14所示,该平台基于SANYE LIGHT开源飞控构成,搭载了惯性测量单元、OpenMV机器视觉模块、超声波传感器等设备。OpenMV以STM32F427为核心,集成了OV7725摄像头芯片,是一个开源,低成本、功能强大的机器视觉模块,其中OV7725摄像头为下视安装,分辨率为320×240像素,视场角110°,提供硬件二值化的黑白图像。组合导航系统以25 Hz的频率融合传感器的数据。

图14 成像、惯性与高度组合导航实验平台
4.2 实验结果与分析
本文设计了两个实验,在室内实时飞行条件下,分别对高度进行估计以及平移速度估计实验。实验中,通过卡尔曼滤波器将视觉传感器、惯性测量单元的加速度数据和高度传感器信号进行融合,所用的卡尔曼滤波器函数由OpenCV库提供,它可以执行所有与状态估计和数据融合相关的任务。
4.2.1 高度估计实验
本实验的目的在于:验证成像、惯性与高度传感系统通过卡尔曼滤波融合后估计四轴飞行器高度的可靠性。在实验中,成像信息由视觉传感器获取,惯性传感器如陀螺仪、加速度计能够精确的测量角速度的快速变化和线加速度,而高度测量值由超声波传感器提供,以着陆标志为中心,通过人工控制将四轴飞行器的飞行高度从60 cm升至180 cm。
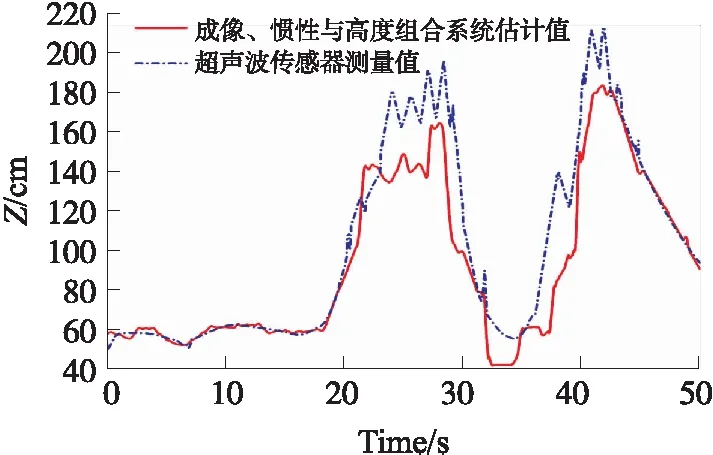
图15 实时高度估计曲线图
如图15所示,通过数据融合成像、惯性与高度组合系统估计的高度值与超声波传感器测量出来的高度具有一致性,证明成像、惯性与高度传感系统能够很好的描述四轴飞行器的飞行高度估计。然而它们之间存在一些差异,根据推测,视觉算法在获取高度值的过程中选取了一些异常值,造成融合后的部分曲线与超声波估计曲线存在差异,通过优化后的滤波算法过滤掉超出正常范围的测量值是可行的方案之一。
4.2.2 平移速度与相对位置估计实验
本实验视觉部分提供无人机相对固定参考系的三维位置,惯性传感器部分提供无人机质心的加速度,研究的目的在于:通过卡尔曼滤波器融合成像与惯性传感器所提供的信息对四轴飞行器平移速度进行准确的估计。
以着陆标志为中心点,四轴飞行器在到达1.5 m实验高度时通过人工进行控制,到达临界点时,由视觉系统计算当前状态下四轴飞行器的三维位置(0,0,1.5),作为实验参考位置。
实验中,过程和观测噪声分别为w=0.150和v=0.100。图16为实验中四轴飞行器平移速度估计曲线图,可以看到卡尔曼滤波器得到的速度估计值很平滑,系统响应更理想。图17为将卡尔曼滤波器融合后的速度作为PID反馈,控制四轴飞行器保持在原点附近飞行。结果显示,飞行器的位置接近期望值:PID控制器成功地将四轴飞行器的x方向位置保持在原点附近,将y方向位置保持在-1.0 m附近,高度位置的最大误差在0.3 m之内。
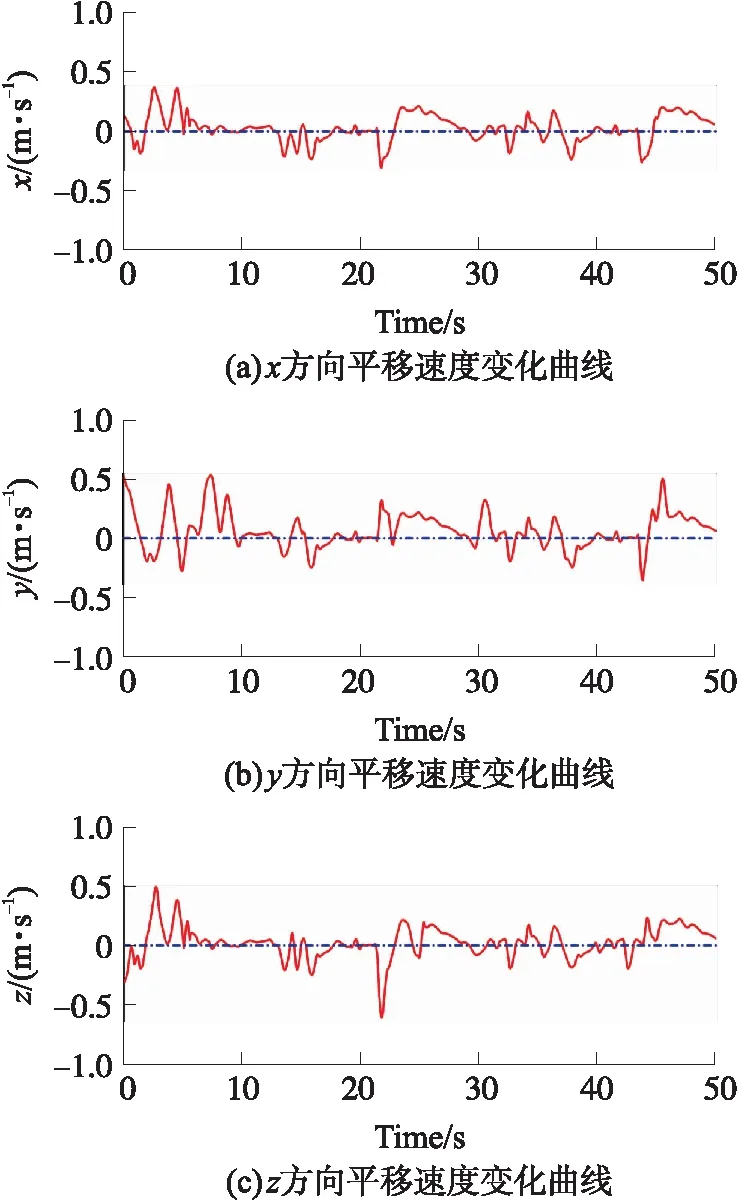
图16 四轴飞行器x,y,z方向平移速度变化过程
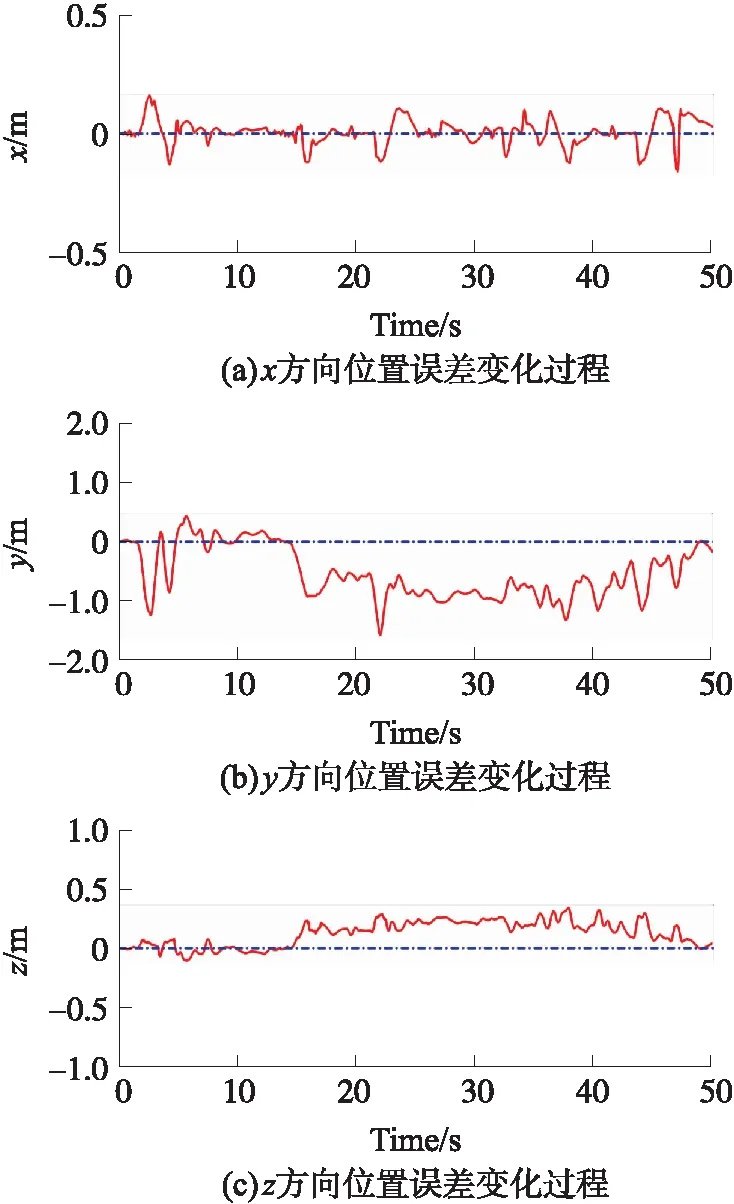
图17 四轴飞行器x,y,z方向误差变化过程
5 总结
本文针对在非结构化、室内和GPS失效的情况下,实现四轴飞行器自主起飞、相对定位和着陆于“无人机自动充电平台”的目的,提出了一种基于卡尔曼滤波的四轴飞行器成像、惯性与高度组合导航系统。视觉系统用于估计四轴飞行器在固定惯性坐标系下的三维位置(x,y,z),惯性测量系统用于提高飞行器线性加速度的估计性能,PID控制器能够利用估计的速度数据稳定飞行器的三维位置。
实验结果表明,成像、惯性与高度传感系统能够很好的描述四轴飞行器的飞行高度估计以及通过卡尔曼滤波器融合成像与惯性传感器所提供的信息能够对四轴飞行器平移速度进行准确的估计。但组合导航与超声波传感器出现了一些差异,需要进一步解决。同时,当进行PID控制时,调整控制器参数很复杂,目前控制器的增益只能通过以实验经验为主进行调整,而系统辨识算法可以估计飞行器的参数,看起来是一个很好的途径。
