统计只是综合演练A卷

■刘中亮 卢欢欢

一、选择题

1.某城区有农民、工人、知识分子家庭共计2007户，其中农民家庭1600户，工人家庭304户。现要从中抽取容量为40的样本，则在整个抽样过程中，可以用到下列抽样方法中的（ ）。

A．系统抽样和分层抽样

B．简单随机抽样和分层抽样

C．分层抽样

D．简单随机抽样，系统抽样和分层抽样

2.一位母亲记录了自己儿子3～9岁的身高数据（略），由此建立的身高与年龄的回归模型为ˆy=7.19x+73.93，用这个模型预测这个孩子10岁时的身高，则正确的叙述是（ ）。

A．身高一定是145．83 c m

B．身高在145．83 c m 以上

C．身高在145．83 c m 左右

D．身高在145．83 c m 以下

3.下列图形中具有相关关系的两个变量是（ ）。

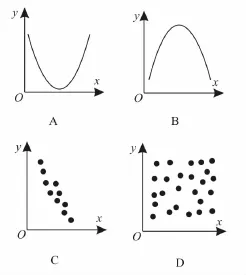
4.某钢铁研究所经研究得到结论，废品率x%和每吨生铁成本y（元）之间的回归直线方程为ˆy=256+2x，这表明（ ）。

A.废品率每吨增加1%，生铁成本增加258元

B.废品率每吨增加1%，生铁成本增加2元

C.废品率每吨增加1%，生铁成本每吨增加2元

D.废品率不变，生铁成本为256元

5.我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题：粮仓开仓收粮，粮农送来米1512石，验得米内夹谷，抽样取米一把，数得216粒内夹谷27粒，则这批米内夹谷约（ ）。

6.在某校连续5次考试成绩中，统计甲，乙两名同学的数学成绩得到如图1所示的茎叶图。已知甲同学5次成绩的平均数为81，乙同学5次成绩的中位数为73，则x+y的值为（ ）。

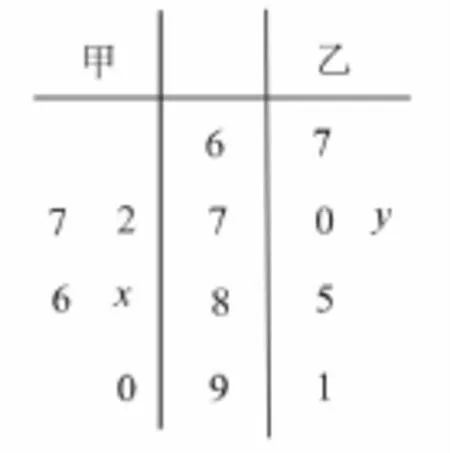
图1

7.最小二乘法的原理是（ ）。

8.图2是某次拉丁舞比赛7位评委为甲，乙两名选手打出的分数的茎叶图（其中m为数字0～9中的一个），去掉一个最高分和一个最低分后，甲，乙两名选手得分的平均数分 别 为a1，a2，则a1，a2的 大 小 关 系是（ ）。

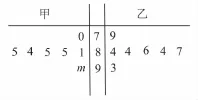
图2

9.表1是某小卖部统计出的5天中卖出热茶的杯数与当天气温的对比表。若卖出热茶的杯数y与气温x近似地满足线性关系，则其关系式最接近的是（ ）。

表1

10.容量为100的样本，其数据分布在［2，18］内，将样本数据分为4组：［2，6），［6，10），［10，14），［14，18］，得到频率分布直方图如图3所示，则下列说法不正确的是（ ）。

图3

A.样本数据分布在［6，10）的频率为0.32

B.样本数据分布在［10，14）的频数为40

C.样本数据分布在［2，10）的频数为40

D.估计总体数据大约有10%分布在［10，14）

11.有关部门从甲，乙两个城市所有的自动售货机中随机抽取了16台，记录上午8：00～11：00间各自的销售情况（单位：元），用茎叶图表示（如图4）。设甲，乙的平均数分别为，标准差分别为s1，s2，则（ ）。

图4

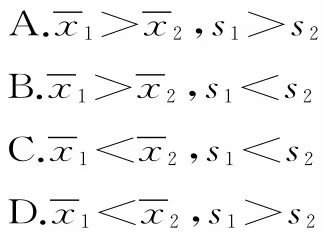
12.有一个容量为45的样本数据，分组后各组的频数如下：［12.5，15.5］，3；（15.5，18.5］，8；（18.5，21.5］，9；（21.5，24.5］，11；（24.5，27.5］，10；（27.5，30.5］，4。由此估计，不大于27.5的数据约为总体的（ ）。

13.10名工人某天生产同一零件，生产的件数是15，17，14，10，15，17，17，16，14，12。设其平均数为a，中位数为b，众数为c，则（ ）。

14.样本a1，a2，…，a10的平均数为a，样本的平均数为那么样本a1，b1，a2，b2，a3，b3，…，a10，b10的 平 均 数是（ ）。

15.为研究变量x和y的线性相关性，甲，乙两人分别进行了研究，利用线性回归方法得到回归直线方程l1和l2，计算知相同，也相同，则l1与l2的关系为（ ）。

16.已知两个变量x，y之间具有线性相关关系，测得（x，y）的四组数值分别为（1，2），（2，4），（3，5），（4，7），则y与x之间的回归直线方程为（ ）。

17.设有两组数据x1，x2，…，xn与y1，，它们的平均数分别是和则新的一组数据2x1—3y1+1，2x2—3y2+1，…，2xn—3yn+1的平均数是（ ）。

18.在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有再发生规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”。根据过去10天甲，乙，丙，丁四地新增疑似病例数据，一定符合该标志的是（ ）。

A.甲地：总体均值为3，中位数为4

B.乙地：总体均值为1，总体方差大于0

C.丙地：中位数为2，众数为3

D.丁地：总体均值为2，总体方差为3

19.某化工厂为预测某产品的回收率y，需要研究它的原料有效成分含量x之间的相关关系，现取8对观测值，计算得则y对x的回归直线的方程是（ ）。

20.甲，乙，丙三名运动员在某次测试中各射击20次，三人测试成绩的频率分布条形图分别如图5，图6和图7，若s甲，s乙，s丙分别表示他们测试成绩的标准差，则（ ）。

图5

图6

图7

二、填空题

21.在某市“创建文明城市”活动中，对800名志愿者的年龄抽样调查统计后得到频率分布直方图（如图8），但是年龄组为［25，30）的数据不慎丢失，据此估计这800名志愿者年龄在［25，30）内的人数为 。

图8

22.已知x，y的取值如表2所示，从散点图分析，x与y线性相关，且ˆy=k x+1，则k=____。

23.从某小学随机抽取100名同学，将他们的身高（单位：c m）数据绘制成频率分布直方图（如图9）。若要从身高在［120，130），［130，140），［140，150］内的三组学生中，用分层抽样的方法选取18人参加一项活动，则从身高在［140，150］内的学生中选取的人数为____。

表2

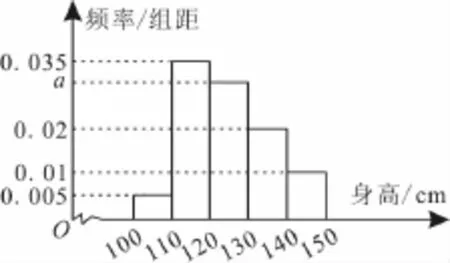
图9

24.某中学为了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，结果用图10所示的条形图表示。根据条形图可得这50名学生这一天平均每人的课外阅读时间为____。

图10

25.对具有线性相关关系的变量x，y有观测数据（xi，yi）（i=1，2，…，10），它们之间的线性回归方程是，若则

26.为弘扬我国优秀的传统文化，某小学六年级从甲，乙两个班各选出7名学生参加成语知识竞赛，他们取得的成绩（满分100分）的茎叶图如图11所示，其中甲班学生的平均分是85，乙班学生成绩的中位数是83，则的值为____。

图11

27.某次考试有64名考生，随机编号为0，1，2，…，63，依编号顺序平均分成8组，组号依次为1，2，3，…，8。现用系统抽样的方法抽取一个容量为8的样本，若在第1组中随机抽取的号码为5，则在第6组中抽取的号码为____。

28.由一组样本数据对两个变量x，y进行回归分析，得到一组样本数据为（x1，y1），（x2，y2），…，（xn，yn），得到的线性回归方程为，那么下列说法正确的是____。（把正确的序号都填上）

三、解答题

29.观察研究某种植物的生长速度与温度的关系，经过统计，得到生长速度（单位：mm/月）与月平均气温（单位：℃）的对比表，如表3所示。

表3

（1）求生长速度y关于温度t的线性回归方程。

（2）利用（1）中的线性回归方程，分析气温从—5℃至20℃时生长速度的变化情况，如果某月的平均气温是2℃时，预测这月该种植物大约能生长多少。

30.节能减排以来，兰州市100户居民的月平均用电量（单位：度），以 ［160，180），［180，200），［200，220），［220，240），［240，260），［260，280），［280，300］分组的频率分布直方图如图12所示。

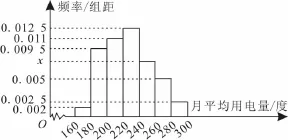
（1）求直方图中x的值。

（2）求月平均用电量的众数和中位数。