立体几何基础训练A 卷参考答案
2019-02-26
一、选择题
1.D 2.A 3.C 4.D 5.A 6.B
7.C 8.C 9.B 10.B 11.A 12.C
二、填空题

三、解答题
17.(1)连接PB,因为G,F分别是PC,BC的中点,所以GF∥BP,所以PB与BB1所成角即为FG与BB1所成角。
在R t△PB1B中,由,可得,所以FG与BB1所成角的大小为30°。
(2)由(1)可得,直线FG∥平面ABB1A1,因为E是AC的中点,所以EF∥AB。
因为AB⊂平面ABB1A1,EF⊄平面ABB1A1,所以EF∥平面ABB1A1。
因为EF与FG相交,EF⊂平面EFG,GF⊂平面EFG,所以平面EFG∥平面ABB1A1。
18.如图1,以D为坐标原点,建立坐标系D-x y z。设正方体的边长为2,则D(0,0,0),A(2,0,0),B(2,2,0),E(1,2,0),F(2,1,2),G(1,2,2)。

图1
又平面ABD的一个法向量(0,0,2),所以因此
19.(1)由PD⊥AB,PD⊥BC,AB∩BC=B,得PD⊥平面ABCD,从而PD⊥AD。在△ABD中,由余弦定理得,BD2=则有AD2+BD2=AB2,所以∠ADB=90°,即AD⊥DB。又PD∩DB=D,则有AD⊥平面PDB,故AD⊥PB。

图2
(2)以D为原点,建立如图2所示的空间直角坐标系D-x y z,设
设平面APB的一个法向量为m=(x,则
设平面PBC的一个法向量为n=(x,y,z),则有
20.(1)因为A'D⊥A'E,A'D⊥A'F,所以A'D⊥平面A'EF。又EF⊂平面A'EF,所以A'D⊥EF。由已知可得EF⊥BD,所以EF⊥平面A'BD。。又A'D⊥平面A'EF,A'M⊂平面A'EF,所以A'D⊥A'M。在R t△A'DM中,sin∠A'DM

图3
(2)由(1)知平面A'BD⊥平面BEDF,则∠A'DB为A'D与平面BEDF所成角。设BD,EF交于点M,连接A'M,如图3,则A'M,所以A'D与平面BEDF所成角的正弦值为

图4
21.(1)如图 4,取AD的中点M,连接CM,AB=AF=BC=2,BCAM,故四边形ABCM为平行四边形,可知。在△ACD中,有∠ACD=90°,所以AC⊥DC。又AC⊥EC,DC∩EC=C,所以AC⊥平面CDE。因为ED⊂平面CDE,所以DE⊥AC。又DE⊥AD,AD∩DE=D,所以DE⊥平面ABCD。因为DE⊂平面ADEF,所以平面ABCD⊥平面ADEF。
(2)由(1)知平面ABCD⊥平面ADEF,作BH⊥AD,所以BH⊥平面ADEF,BH,连接AE,所以
22.(1)因为三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,所以以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立如图5所示的空间直角坐标系。因为AB=AC=AA1=1,E,F分别是棱C1C,BC的中点,所以。因为,所以B1F⊥AE,B1F⊥AF。因为AE∩AF=A,所以B1F⊥平面AEF。
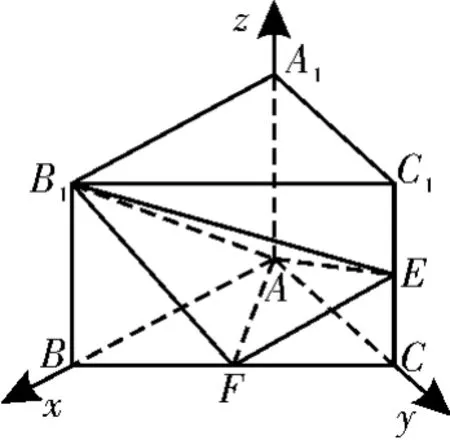
图5
设平面EFB1的法向量为则1,得n=(1,1,0)。
设平面AB1E的法向量为m=(x,y,z),则取x=2,得m=(2,1,-2)。
设二面角F-B1E-A的大小为θ,则cosθ所以θ=45°,即二面角F-B1E-A的大小为45°。
(3)因为平面AB1E的法向量m=(2,1,,所以点F到平面EAB1的距离
