立体几何中的易错题归类剖析
2019-02-26河南省沈丘县第一高级中学赵向前
■河南省沈丘县第一高级中学 赵向前
一、求几何体的外接球时,易忽视球的几何性质
考点指南:球的问题是平面图形圆的立体化、空间化问题,圆的考点在高中侧重解析几何问题的考查,即与圆的方程有关的问题,高中圆的几何特性(几何图形的外接圆)主要体现在空间几何体的外接球的知识方面,即求解与几何体的外接球有关的问题时,需要把立体球转化为平面圆进行分析,考查层次属于有难度的问题。
例1 一个几何体的三视图如图1所示,求该几何体外接球的表面积。(单位:c m)

图1
解题分析:根据题意知该几何体是一个圆锥,其轴截面是边长为2c m的正三角形,则几何体及其外接球的直观图如图2所示。由题可知轴截面△PAB为正三角形,球心O为正三角形的重心,根据三角形重心的知识,则PO∶OO'=2∶1。又O'为AB的中点,所以在R t△PAO'中,所以
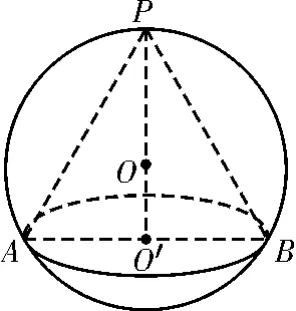
图2
因为△PAB是正三角形,PO=AO,则外接球的半径为所以圆锥的外接球的表面积
考查意图:本题主要考查同学们的空间想象能力、空间问题平面化能力及计算能力。虽然本题是求解外接球的表面积,但是在求解球的半径时,需要逐步进行,故对运算逻辑也是有考查的。
复习建议:由于高考是选拔性考试,考题定位“源于课本,考查分析问题与求解问题的能力”,学习中,应立足教材,对教材中的核心题型,比如求三棱锥的外接球,只有做好归纳总结,步骤细化,有了基本方法的掌握,才能在解决柱体、锥体的问题中做到熟练掌握与应用。
变式练习1:如图3,在四棱锥P-ABCD中,面PAB⊥面ABCD,△PAB是等边三角形,四边形ABCD为矩形,边长AB=2,AD=4,求四棱锥P-ABCD的外接球的体积。
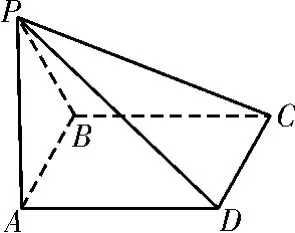
图3
解题分析:如图4,构造四棱锥P-ABCD的外接球O,因为△PAB为正三角形,正△PAB的外接圆为☉O2,根据三角形重心的知识,则PO2∶O2E=2∶1。
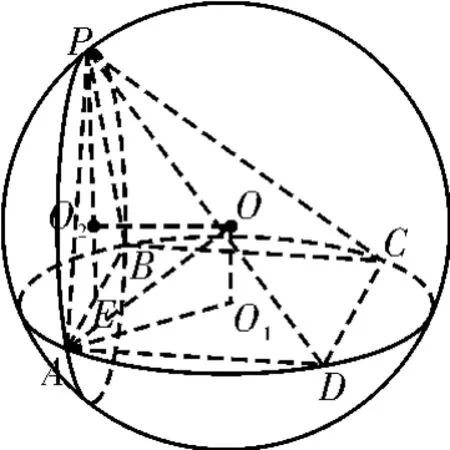
图4
因为AB=2,所以则
在矩形ABCD中,AO1是对角线的一半,所以R t△OO1A中,,即四棱锥P-ABCD的外接球O的半径为
二、判断线面关系时,易忽视几何载体或空间几何常识的应用
考点指南:有关线面关系的问题,属于考题中的小题部分,出题灵活,考查点线面的空间位置关系,在分析过程中,需要借助不同的几何体或线面关系去呈现,考生在做题时,由于线面垂直、平行及判定性质(八大定理)同时出现,易脱离几何载体或忽略几何常识。在简易逻辑问题上,条件的考查对考生来说比较抽象,特别是p是q的什么条件,或p的什么条件是q等知识的考查,属于基础题型中易于出错的部分。
例2 设m,n是平面α内的两条不同直线,l,s是平面β内两条相交直线,则α⊥β的一个充分不必要条件是( )。
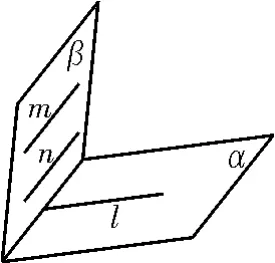
图5
解题分析:本题给出空间中两线两面,从线面关系去证明面面垂直,需要考虑证明面面垂直的基本方法,就是线面垂直的判定定理或直二面角知识。如图5中,α,β斜交,知A,D选项错误,直线l⊥a。图6中,α,β斜交,m⊥l,n⊥s,知C选项错误。B选项是线面垂直的判定定理,故B选项正确。
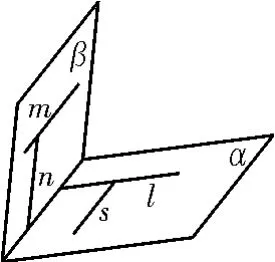
图6
考查意图:简易逻辑中的条件结合空间点线面知识,属于基础问题的综合,体现知识的交叉情况,立足空间几何直观和几何载体,注重对考生基础能力、基本方法应用能力的考查。
复习建议:在基础问题方面,紧扣数学核心知识及考点,准确掌握概念,平时注重常规问题的分析,简单不出错,拿准分才是考生应该锻炼的。
变式练习2:已知不同的直线l,m,n,平面α,β,γ,则下列关于线面关系的说法中正确的是( )。
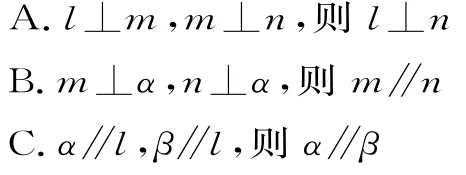
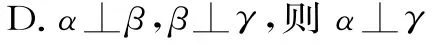
解题分析:A选项中的直线l与直线n之间还存在平行、相交、异面的情况;B选项正确,直线重合的情况,在本题不会出现,考生不用纠结;选项C、D中的两个平面可能存在平行、垂直、相交的情况。
三、证明平行问题时,易忽视经典平行证明方法的应用
考点指南:线面的平行问题,是高考立体几何问题中的核心证明问题,与线面垂直处于同样重要的地位。在人教A版《数学必修2》中,关于线面平行有两个判定定理与两个性质定理。虽然可以用向量证明平行与垂直问题,但高考中的立体几何解答题,其第一问一般考查平行与垂直,主要用定理去证明,应用时,结合具体问题,平行因素体现在比例或中点问题上。方法一,构造面面平行;方法二,通过中位线、比例、平行四边形证明线线平行。
例3 如图7,P是平行四边形ABCD平面外一点,M,N分别是PA,BD上的点,且求证:MN∥平面PDC。
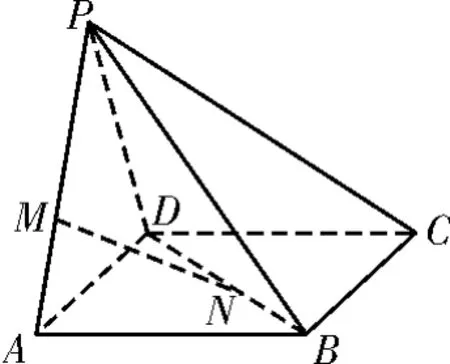
图7
解题分析:由题知,该图形可看作四棱锥
如图8,在AD上取一点Q,满足,即Q是AD的三等分点,连接MQ,NQ。在△ADP和△DAB中,MQ∥PD,NQ∥AB。

图8
在平行四边形ABCD中,AB∥CD,所以NQ∥CD。
又MQ∩NQ=Q,CD∩PD=D,所以面MNQ∥面PCD。
又MN⊂面MNQ,所以MN∥面PCD。
考查意图:本题通过比例给出条件去求证平行,对比中点问题,考生易构造中位线在面内寻找线线平行,但通过构造面面平行,用面面平行的判定定理是比较好的方法。本题考查考生对平行问题的常见证明方法的理解与应用情况。
复习建议:立体几何是高考的必考点,在解答题型中证明问题与求解问题属于中等难度题型,对比圆锥曲线与函数问题,考生易得分,复习时要熟练掌握基本定理,解题时步骤要写详细,保证得分点突出。注意经典题型与构造问题,做好积累归纳。
变式练习3:如图9,在四棱锥P-ABCD中∠BAD= ∠ABC=90°,E是PD的中点。证明:直线CE∥面PAB。
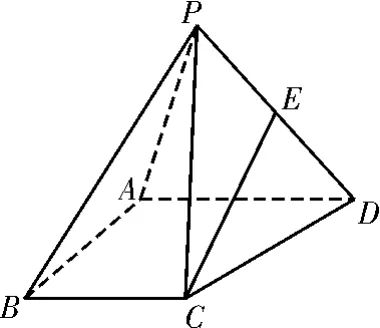
图9
解题分析:如图10,在四棱锥P-ABCD中,取AD的中点F,连接∠ABC=90°,则四边形ABCF为正方形,所以AB∥CF。

图10
在△PAD中,EF是中位线,故PA∥EF。
又AB∩PA=A,EF∩FC=F,所以面PAB∥面EFC。
又直线CE⊂面EFC,所以直线CE∥面PAB。
四、应用向量法求空间角时,易忽视坐标系的建立
考点指南:立体几何属于高考中等难度的问题,考生易得分,空间问题的求解比证明复杂一些,在2010年之前,求解空间角常采用直接构造,对空间想象能力要求比较高,难度比较大,近些年,考查思路转化到代数方法,就是用空间向量去求解,空间向量的运算比构造角的三角形计算,计算量小一些,对考生的考查进一步体现数学的基础性、工具性。建立空间坐标系,通过向量运算证明空间垂直问题,不可小看。
例4 如图11,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF。求DP与平面ABFD所成角的正弦值。

图11
解题分析:由已知的垂直条件可得PF⊥BF,BF⊥EF,所以BF⊥平面PEF。
又线BF⊂面ABFE,所以平面PEF⊥平面ABFD。
过点P作PH⊥平面ABFD,则点H在平面PEF与平面ABFD的交线EF上,过H在面ABFD上作HQ⊥EF,以H为坐标原点,以HQ,HF,HP所在直线为坐标轴,建立空间坐标系,如图12所示。

图12
由于F为正方形的边BC的中点,设BF=1,则PF=1,DP=2,DE=1。
在R t△PED中
在△PEF中,PE2+PF2=EF2,所以△PEF是直角三角形。
设直线PD与平面ABFD所成角为θ,
所以PD与平面ABFD所成角的正弦值是
考查意图:本题通过翻折,把正方形问题转化为空间几何问题,通过翻折前后的垂直关系,考查线面垂直的证明与应用,求解线面角时,可采用直接构造线面角,难度在于垂线的分析,即垂足位置,采用空间坐标系,考查点的坐标的求解,经典的直角三角形求边长,是不容忽视的问题。
复习建议:在坐标系建立问题上,梳理归纳考题中的垂直因素:①线面垂直,可以直接用;②面面垂直,融合等腰的中点问题,采用三线合一;③空间几何体,出现斜棱柱或者翻折问题,抓住垂直问题的证明去建立垂直。
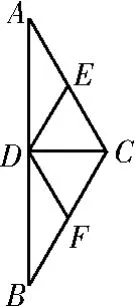
图13
变式练习4:如图13,在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B,如图14。
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E-DF-C的余弦值。
解题分析:(1)如图14,在△ABC中,由E,F分别是AC,BC的中点,得EF∥AB。又AB⊄平面DEF,EF⊂平面DEF,所以AB∥平面DEF。

图14
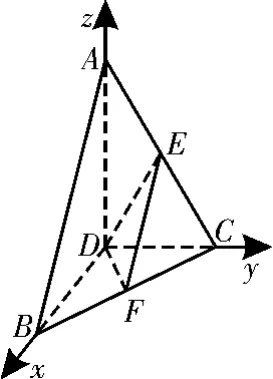
图15
(2)以点D为坐标原点,直线DB,DC,DA为x轴,y轴,z轴,建立空间直角坐标系,如图15所示。设CD=a,则AC=BC则
取平面CDF的法向量为m=(0,0,1),设平面EDF的法向量为n=(x,y,z),则
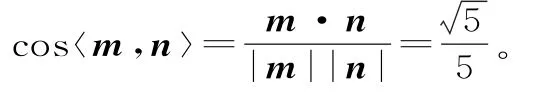
所以二面角E-DF-C的余弦值为
变式练习5:如图16,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC。
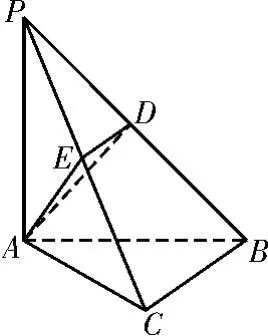
图16
(1)求证:BC⊥ 平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值。
解题分析:(1)因为PA⊥底面ABC,所以PA⊥BC。
又∠BCA=90°,所以AC⊥BC。
所以BC⊥平面PAC。
(2)因为D为PB的中点,DE∥BC,所以三角形,所以
在 R t△ABC中,∠ABC=60°,所以
由(1)知BC⊥平面PAC,所以DE⊥平面PAC,垂足为点E,所以∠DAE是AD与平面PAC所成的角。
因为PA⊥底面ABC,所以PA⊥AB。
又PA=AB,所以△ABP为等腰直角
在 R t△ADE中
