黄土区不同土层土壤容重空间变异与模拟*

于冬雪 贾小旭† 黄来明 邵明安 王 娇

（1 中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室，北京 100101）

（2 中国科学院大学资源与环境学院，北京 100190）

土壤容重（Bulk density, ρb）是土壤基本物理性质之一，是衡量土壤质量和土壤生产力的重要指标［1］，对土壤的透气性、入渗性能、持水能力、溶质迁移特征以及土壤的抗侵蚀能力均有显著影响［2］，也是评估土壤有机碳和养分贮量的重要参数［3-4］。土壤容重的大小与空间分布受土壤质地与结构、土地利用方式、地形、气候等因素的影响［2,5-8］。黄土高原地形复杂多变、水土流失严重，了解黄土区土壤容重的空间变异规律及其影响因素，建立适于该区土壤容重的统计预测模型，有助于为该区的水土流失与侵蚀预报提供基本参数。

目前，已有大量学者对不同尺度下土壤容重的空间异质性进行研究，并取得重要进展［2-3,7,9-14］。耿韧等［11］研究了黄土丘陵区浅沟表层土壤容重的空间变异特征，发现土壤容重从浅沟上部到下部总体上呈逐渐减小的趋势，土壤容重的空间异质性以各向同性为主；傅子洹等［12］结合经典统计学与地统计学方法，研究了黄土高原小流域尺度土壤容重的时空变化规律，发现小流域土壤容重在月际尺度上变化趋势较为一致，表层土壤容重总体差异较小；易小波等［13］采用经典统计学方法分析了黄土高原南北样带不同土层深度土壤容重的变异特征，发现0～20 cm土壤容重为中等程度变异，20～40 cm为弱变异；柴华和何念鹏［14］基于全国3 361个样地的11 845个土壤容重数据，全面阐释了中国陆地生态系统土壤容重的基本特征和变异规律，结果表明，土壤容重随土层深度增加而增大，不同土壤类型间的容重具有较大差异，这为准确评估区域乃至全国土壤碳、氮贮量提供了重要参数。

传递函数模型根据容易获得的土壤理化性质可以快速获得不同尺度上的水力参数，其构建方法主要有线性回归、非线性回归、神经网络等［15］。由于大面积直接测量获取土壤容重存在困难，国内外学者利用更易实现的土壤容重传递函数模型来预测土壤容重。Wang等［3］利用传递函数方程对黄土高原区域尺度表层土壤容重进行模拟，结果表明，基于黏粒和粉粒含量、有机碳含量、坡度建立土壤容重传递函数预测模型可以达到合理的精度。然而，该研究只分析了0～25 cm表层土壤容重，未进行土壤容重的分层模拟，而传递函数的重要应用之一就是对深层土壤容重进行模拟预测；韩光中等［8］对中国主要土壤类型的土壤容重传递函数研究发现，基于土壤系统分类的数据分组后建立的土壤容重传递函数能够明显提高预测精度，利用土壤容重传递函数时需注意研究区及适用范围。

纵观已有研究，对黄土高原区域尺度不同土层、不同土地利用方式下的土壤容重空间变异与模拟的研究较少。本研究获取黄土区0～10、10～20和20～40 cm的土壤容重，采用经典统计学与地统计学方法，分析不同土层深度土壤容重的空间变异规律，并基于土壤、地形、土地利用和气候因子，利用多元逐步回归方程和传递函数方程对不同土层的土壤容重进行模拟预测，以期为该区的水土资源管理和生态建设提供基本参数和依据。

1 材料与方法

1.1 研究区概况

黄土高原位于中国西北地区（3 3°4 3′～41°16′N，100°54′～114°33′E），是指日月山、贺兰山以东，太行山以西，秦岭以北，阴山以南的广大地区，面积约为64万km²。该地区气候呈现地带性分布，降水量、平均气温、干燥度均由东南向西北方向递减［16］。年降水量为150～800 mm，且集中在6—9月份，占全年降水量的55%～78%，多年平均降水量为466 mm，年平均气温为3.6～14.3 ℃，年蒸发量为1 400～2 000 mm。典型黄土区特指我国晋、陕、甘、宁、豫、内蒙诸省间黄土分布最连续、厚度最大、侵蚀地形最典型的地段（图1），面积约为43万km²，该区域塬、梁、峁、沟壑等黄土地貌发育最典型，水土流失最严重［17］，是黄土高原进行生态建设的重点区域。

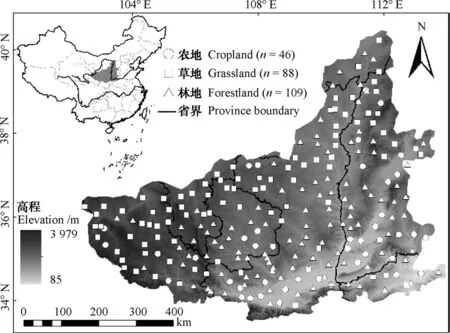
图1 黄土区位置以及采样点分布Fig. 1 Location of the loess area and distribution of the sampling sites

1.2 数据采集与分析

2012年5—8月，以典型黄土区数字化地图为底图，采用间距约为40 km×40 km的网格进行取样。具体为：在野外采样之前，使用GIS软件在典型黄土区的数字地形图上加载一个40 km×40 km的格网作为参考；此外选择合适的道路系统覆盖整个区域构成采样路径，沿着选择的道路方向取样，采样点之间间隔约为40 km。实际采样过程中，具体采样点的原则既要具有随机性且能代表网格范围内的主要土地利用类型、地形特征等。同时，要考虑采样点的可达性和实际的可操作性。在每个样点，利用环刀分3层（0～10、10～20和20～40 cm）采集原状和扰动土壤样品。将原状土壤样品带回实验室，采取烘干法测定其容重。扰动土壤样品自然风干，处理通过1 mm筛孔，经预处理后利用激光粒度仪测定土壤颗粒组成。

为了更好地描述和体现各个网格内地表景观的代表性，取样时选择最能代表该网格土壤和植被类型的样点，若网格内地表景观复杂多变，则考虑适当增加代表其他土地利用方式的样点。经统计，本研究在黄土区共计布设243个样点，其中农地（主要指1年生农作物地）46个，草地（包括人工草地和天然草地）88个，林地（包括天然和人工乔木林及灌木林地）109个（图1）。

利用GPS记录每个采样点的经纬度坐标和海拔，使用罗盘仪测定样点的坡度和坡向，同时记录各样点的土地利用方式和植被类型。为了分析方便，将土地利用方式分别进行数字编码，农地=1，草地=2，林地=3［18］。利用黄土高原74个气象站1951—2012年月尺度气象数据，包括降水量、气温、蒸发量、干燥度（干燥度=蒸发量/降水量），使用反距离加权插值法将各气象要素插值生成空间上连续分布的气象数据（空间分辨率为100 m×100 m），然后提取每一样点的气象数据。由于土壤实际的蒸发量数据难以获取，因此，本文利用气象站常规观测指标—水面蒸发量来反映样点所在地区的蒸发能力。

1.3 经典统计学空间变异分析理论

土壤容重的空间变异特征用变异系数（CV）表示：

式中，S代表标准偏差，x 代表平均值。根据变异程度分级，CV≤100%为弱变异性，10%＜CV＜100%为中等变异性，C V≥1 0 0%为强变异性［2, 19］。

1.4 地统计学空间变异分析理论

地统计学进行空间变量变异特征分析是根据半方差变化规律进行的，半方差函数的计算公式如下：

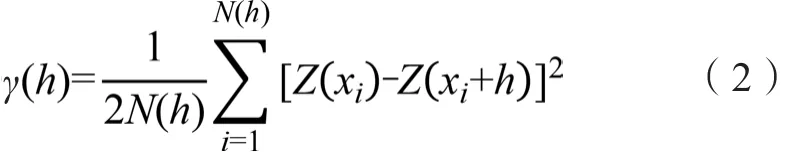
式中，γ(h)代表半方差函数值，N(h)代表相距为的点对数，Z(xi)代表x=xi处变量Z的实测值，Z(xi+h)代表x=xi+h处变量的Z实测值。以滞后距h为横轴，半方差函数值为纵轴可以绘制半方差图。根据半方差图可以得到块金值C0，基台值C0+C，变程A三个重要特征值。C0表示随机部分引起的空间变异性，C0+C表示变量的最大变异程度，A表示变程即变量自相关范围。通过公式C0/(C0+C)计算可以得到一个描述空间变量依赖性的重要指标即空间异质比，根据Cambardella的划分标准［9］，C0/(C0+C)≤25%时表示强的空间依赖性，25%＜C0/(C0+C)＜75%时表示中等空间依赖性，C0/(C0+C)≥75%时表示弱的空间依赖性［2,10,20］。基于半方差函数的最佳拟合模型，利用普通克里格插值得到不同土层土壤容重的空间分布图［10］。

1.5 逐步回归方程和传递函数模型评价指标

本研究采用决定系数（R2）、平均误差（AE）、平均绝对误差（MAE）、均方根误差（RMSE）和模型效率系数（MEC）五个参数来评价逐步回归方程和传递函数模型的精度。其中，决定系数可以表示模型对土壤容重空间变异的解释量，其值越大，说明模拟值所能解释的变异越多。模型效率系数最早被用来评价水文模型的预测效果［21］，其值越接近于1表明精度越高。平均误差、平均绝对误差和均方根误差越小，代表传递函数方程拟合的效果越好，预测的精度越高。

1.6 数据处理

使用Microsoft Excel2013和SPSS20.0进行土壤容重的描述性统计分析、土壤容重与环境因子的皮尔森相关分析和多元逐步回归分析以及不同土层土壤容重的传递函数方程的模拟。利用GS+9.0进行半方差函数模型的拟合，采用ArcGIS10.2地统计模块进行土壤容重的克里格插值及制图。

2 结果与讨论

2.1 土壤容重的基本统计特征

表1显示了不同土层土壤容重的统计特征值。结果表明，3个土层深度中10～20 cm土壤容重的变化范围最大。黄土区0～10、10～20和20～40 cm土壤容重的平均值分别为1.25、1.32、1.37 g·cm-3，这与易小波等［13］所测黄土高原南北样带3个土层土壤容重平均值基本一致，表明黄土区土壤容重随土层深度的增加而增大，主要原因可能是表层土壤有机质含量高，植物根系也主要分布在浅层土壤，土壤孔隙状况良好［22］。Wang等［3］和吕殿青等［23］研究表明容重与有机碳含量和孔隙数量呈负相关关系。经典统计结果表明，3个土层土壤容重的变异系数分别为10.0%、11.4%和10.4%，即3个深度的土壤容重均属于中等程度变异。通过偏度、峰度以及单样本Kolmogorov-Smirnov（K-S）检验来判断容重数据是否符合正态分布，3个土层土壤容重的K-S值分别为0.697、0.130、0.221，表明不同土层容重均符合正态分布，可进行进一步的统计分析。

表1 不同土层土壤容重的描述性统计特征Table 1 Descriptive statistics characteristics of soil ρb relative to soil layer

2.2 基于地统计学的土壤容重空间变异特征

利用地统计半方差理论对不同土层土壤容重的空间变异性进行分析，结果见表2。0～10和10～20 cm土壤容重的最佳拟合模型均为指数模型，20～40 cm土壤容重最佳拟合模型为球状模型，最佳拟合模型的决定系数均较高，表明所选模型能够很好地反映土壤容重的空间变异特征。3个土层的块金值变化范围为0.002～0.013，表明随机因素引起的土壤容重变异性较小。空间异质比分别为13.3%、50.0%和50.0%，表明0～10 cm土壤容重具有强烈的空间依赖性，10～20和20～40 cm土壤容重具有中等程度的空间依赖性［3,13］。因此，底层土壤容重由随机因素引起的变异性更强。0～10 cm容重变程为22.3 km，10～20和20～40 cm变程分别为283.4 km和781.5 km，表明10～40 cm深度土壤容重空间连续性的尺度范围更大。根据Flatman 和Yfantis［24］的建议，最佳采样间距为变程的1/4～1/2，因此，3个土层深度容重最佳采样间距分别为5.6～11.2 km、70.9～141.7 km和195.4～390.8 km。0～10 cm容重变程大于理论最佳采样间距，为了达到反映其空间结构的目的，该土层深度需要减小采样间距，增加采样点数量，而10～40 cm土层可增大采样间距，适当减少采样数量。

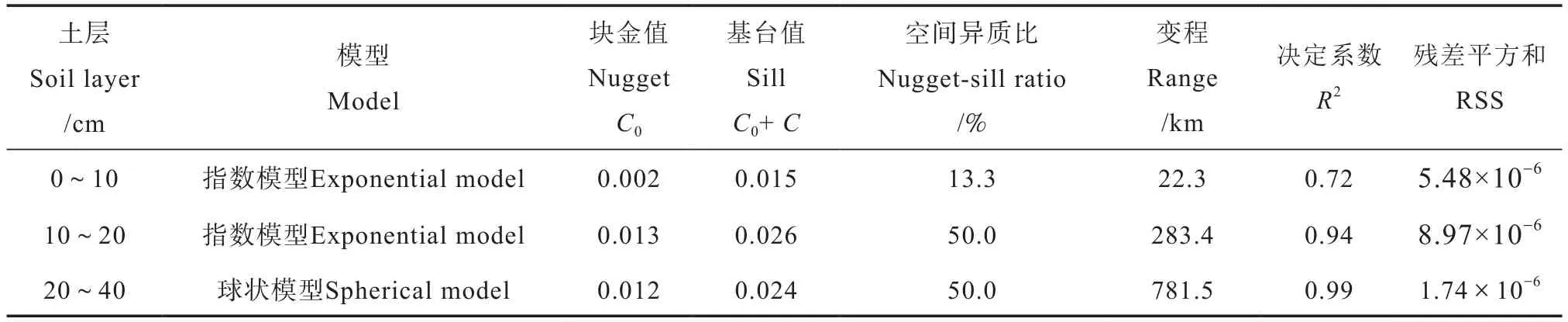
表2 不同土层土壤容重的半变异函数模型及其结构参数Table 2 Semivariance model and structural parameters of soil ρb relative to soil layer

2.3 土壤容重的空间分布格局

为了直观地反映黄土区不同土层土壤容重的空间分布情况，基于半方差函数的建立，采用普通克里格插值法对3个土层深度土壤容重进行空间插值。由图2可以看出，不同土层土壤容重的连续性较好。总体而言，0～10 cm土层容重表现为黄土区内的甘肃、陕西中部和山西中部较低，20～40 cm土壤容重表现为黄土区内的陕西南部、河南和内蒙古较高。这可能是因为陕西南部和河南主要的土地利用类型为农地，农业活动导致犁底层被压实，因而土壤容重较大。从局部来看，部分地区会出现土壤容重偏大或者偏小的值，这可能与人类的扰动、牧群的践踏、鼠群的活动、植物的斑块化生长有关［25］。

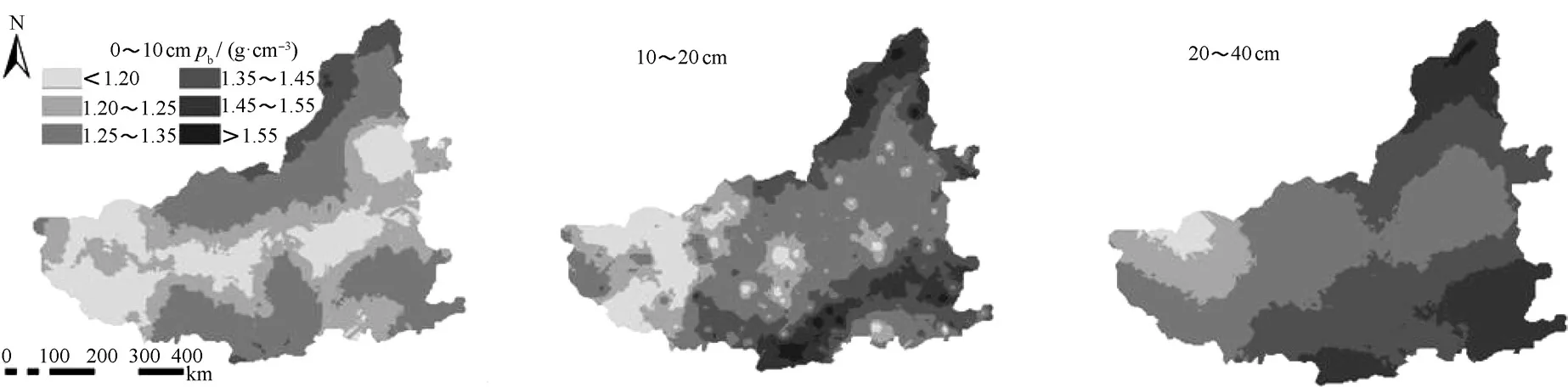
图2 黄土区不同土层土壤容重的空间分布图Fig. 2 Spatial distribution of soil ρb relative to soil layer in the loess area

2.4 土壤容重与各变量的Pearson相关性

土壤容重在不同尺度下受土壤类型、气候、地形、土地利用以及生物扰动等因素的综合影响［7,12］，因此，本研究选取11个可能影响土壤容重的环境因子（包括黏粒、粉粒、砂粒、土地利用方式、海拔、坡度、坡向、多年平均降水量、多年平均气温、蒸发量和干燥度）进行Pearson相关性分析，以期揭示区域尺度与土壤容重显著相关的因素。对11个因子进行单样本K-S检验，发现砂粒含量、坡度、多年平均气温和干燥度4个因子经过对数转换后符合正态分布，故对此4个因子进行对数转换后做进一步分析。

表3为不同土层土壤容重与土壤、气候、地形和土地利用方式的皮尔森相关分析结果。可以看出，3个土层土壤容重与粉粒含量均呈极显著负相关关系。粉粒含量的增加，可使土壤孔隙结构和透气性有较大提高，从而导致土壤容重降低［3］。3个土层深度土壤容重均与海拔和坡度呈显著负相关关系，可能是由于海拔较高、坡度较大的样点土壤易被侵蚀，土壤较松散，以致土壤容重较小。此外，坡度较大的地方，受动物或人为活动干扰较小，故在一定程度上也可减小对土壤的压实。此外，3个土层深度土壤容重均与土地利用方式呈显著负相关关系。

针对土地利用方式对土壤容重的影响进行了单因素方差分析（图3）。结果表明，对于同一种土地利用方式，土层越深，土壤容重越大；对于同一个土层，土壤容重表现为农地最大，草地与林地相近，这与连纲等［7］得到的灌木林地和荒草地土壤容重较大，林地和坡耕地土壤容重较小，梯田土壤容重居中的结果并不一致。这可能与研究区不同有关。本文以整个黄土区为研究对象，农地主要分布在黄土区南部，土壤黏粒含量高，土质密实，而林草地主要分布在黄土区中部和西北部，土壤颗粒组成以粉粒为主，土质疏松，加之林草地土壤根系含量高，人为活动导致的土壤压实干扰小，所以林草地土壤容重较农地小。

2.5 土壤容重多元逐步回归方程和传递函数方程

土壤容重的传统测量方法与近年来出现的间接方法均很难实现大面积的连续测定，故造成土壤容重数据库缺失。因此，利用土壤其他属性来预测土壤容重对完善土壤容重数据库具有重要意义［8,26］。本研究根据皮尔森相关分析结果，利用243个样点中的80%（195个）作为建模点。选取与每个土层土壤容重显著相关的因子进行多元逐步回归分析，得到3个土层的多元逐步回归方程（表4）；结合与每个土层土壤容重显著相关的因子及其6种常见的转换函数（对数、倒数、平方、开方、余弦、显著相关因子两两相乘）作为自变量进行逐步回归分析，将通过显著回归的因子进行线性回归，得到3个土层土壤容重的传递函数方程（表4）。

结果表明，3个多元逐步回归方程均包含粉粒含量、海拔、土地利用方式。不同土层深度的传递函数方程包含的变量不同，0～10 cm主要为粉粒含量、土地利用方式、海拔以及坡度，10～20 cm主要为粉粒含量、海拔、多年平均气温、干燥度及土地利用方式，20～40 cm主要为粉粒含量、海拔、土地利用方式、多年平均降水量、坡度及干燥度。结合皮尔森相关分析、多元逐步回归方程以及传递函数方程模拟结果可以看出，黄土区土壤容重受土壤、地形、土地利用方式、气候等大尺度与小尺度因子的综合影响。

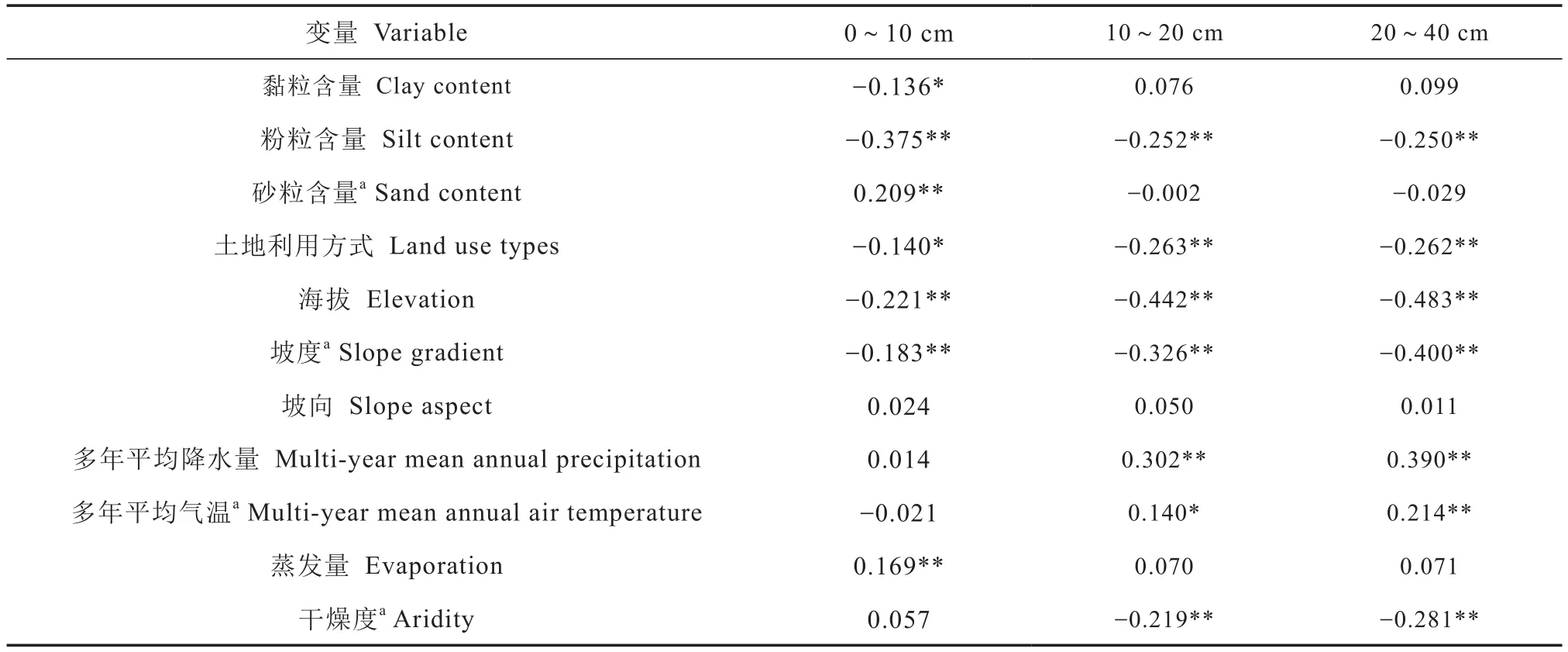
表3 不同土层土壤容重与各变量的Pearson相关系数Table 3 Pearson's correlation coefficients between soil ρb and other variables relative to soil layer

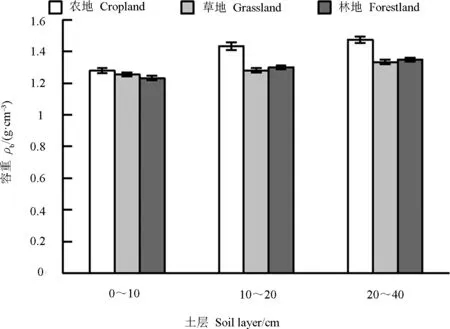
图3 不同土地利用方式下土壤容重单因素方差分析（平均值±标准误差）Fig. 3 One-way analysis of variance of soil ρb relative to land use (mean ± standard error)

利用243个样点中的20%（48个）进行模型精度验证，验证结果见表4。多元逐步回归方程3个土层的决定系数R2分别为0.39、0.35、0.34，传递函数方程3个土层土壤容重的决定系数R2分别为0.40、0.38和0.52。因此，两种方法对0～10 cm土层土壤容重的模拟效果相近，可以解释土壤容重空间变异的40%。与0～10 cm模拟结果不同，10～20和20～40 cm深度传递函数模型模拟效果明显优于逐步回归方程，模拟精度较逐步回归方程分别提高3%和18%。传递函数方程平均误差、平均绝对误差均小于0.1，均方根误差均小于0.2，模型效率系数也均超过0.3，精度验证参数总体优于多元逐步回归方程，表明传递函数方程在预测底层土壤容重方面效果更佳。这主要是因为传递函数方程包含了不同变量的转换，可以更好地描述变量与容重之间的关系［3］。同时，根据Leij等［27］提出的地形因子可以提高传递函数模型的效率，本研究将坡度、海拔等地形因子均考虑在内。此外，Han等［28］研究表明土壤容重与土层深度呈显著正相关，本研究对不同土层土壤容重分别进行模拟，可剔除土层深度对模拟效果的干扰。与Wang等［3］研究相比，本研究采集的样点土层更深，因而对深层土壤容重研究更具有指导意义。此外，传递函数模型中容重的影响因子也较容易获取，因此，该传递函数模型可用于田间条件下黄土高原区域尺度不同土层土壤容重的模拟与预测。

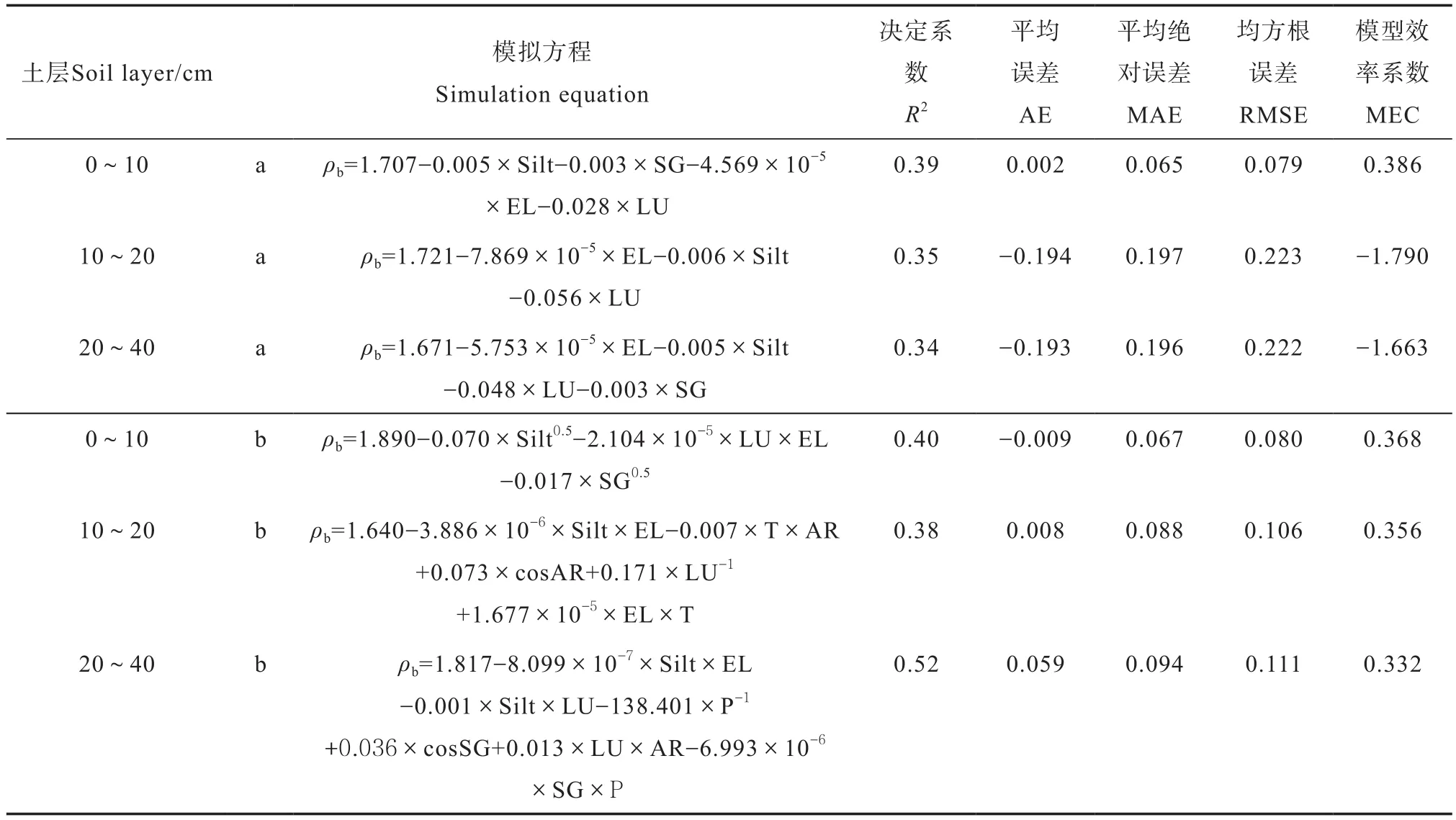
表4 不同土层土壤容重模拟的多元逐步回归方程（a）、传递函数方程（b）和预测精度Table 4 Simulation of soil ρb with multi stepwise regression equation(a), and pedotransfer function equation(b) and their prediction accuracies

3 结 论

黄土区不同土层、不同土地利用方式下土壤容重的空间分布具有显著差异，土壤容重随土层深度的增加而增大，且不同土层中农地的容重最大，其次为林地和草地。0～10 cm容重具有强烈的空间依赖性，而10～40 cm具有中等程度空间依赖性，各土层容重的半变异函数可用指数模型和球状模型进行较好拟合。0～10、10～20和20～40 cm深度土壤容重最佳采样间距分别为5.6～11.2、70.9～141.7和195.4～390.8 km。黄土区不同土层土壤容重空间变异受土壤、地形、气候和土地利用方式的共同影响。0～10 cm主要为粉粒含量、土地利用、海拔以及坡度，10～20 cm主要为粉粒含量、海拔、多年平均气温、干燥度及土地利用，20～40 cm主要为粉粒含量、海拔、土地利用、多年平均降水量、坡度及干燥度。传递函数模型对底层土壤容重模拟效果优于多元逐步回归方程，可用于田间复杂环境条件下区域尺度土壤容重空间分布特征的预测。