基于HyperMesh二次开发的车轮径向台架疲劳分析流程优化
2019-02-26赵唐雷杨宁宁
赵唐雷,杨宁宁
(华晨汽车工程研究院, 辽宁沈阳 110141)
0 引言
车轮是乘用车行走的关键组成部分,一般包含轮胎、轮辐和轮辋,其主要功能是支撑汽车总质量,吸收和缓和汽车行驶过程中路面给予的冲击和振动,平衡汽车行驶过程中不利于驾驶的力,提高汽车的动力性、制动性和通过性。车轮径向疲劳试验是模拟车轮在直线行驶过程中,在承受一定的载荷下,研究车轮结构的强度和疲劳性能,因此车轮台架径向疲劳试验是车辆的一项重要试验内容。在车轮开发阶段,汽车车轮径向台架疲劳有限元分析也是车轮设计中一个非常重要的分析项,这样做能够减少车轮开发周期和开发费用。通常进行车轮径向疲劳分析时,需要将轮胎座区域划分20份以上进行加载,实现车轮滚动过程中的受力模拟,通常在受力区域选择和径向载荷加载时需要不断地重复操作,复杂的重复操作如果发生错误不但会影响计算也会增加建模时间。为优化加载过程,利用HyperMesh二次开发功能,用TCL/TK语言[1]开发车轮径向载荷加载辅助程序,提高分析效率的同时固化分析流程。HyperMesh是一款功能齐全,与大部分主流CAE分析有着良好的接口,并且有丰富的二次开发接口和帮助文档[2]。本文作者运用TCL/TK语言和HyperMesh内置函数在二次开发接口中编写车轮径向力加载辅助程序[3-5],帮助工程师快速完成前处理加载任务。
1 车轮径向疲劳试验流程
车轮径向疲劳试验是模拟车轮在直线行驶过程中,在承受一定的载荷下,研究车轮结构的强度和疲劳性能。通常情况下,试验机是一台带有主动旋转转鼓的设备,转鼓表面带有增加摩擦力的浅突起,转鼓须比试验轮胎接触区宽,当试验进行时车轮与转鼓之间会施加一恒定不变的载荷,加载方向应当垂直于转鼓表面,车轮和转鼓的中心在径向上成一条直线,转鼓轴线与车轮轴线应当平行,转鼓直径为1 708 mm,试验示意图如图1所示,试验机如图2所示。试验时轮胎应当充气,车轮使用规定的螺栓与工装进行连接,并且应当定期检查螺栓预紧力。

图1 车轮径向疲劳试验示意图

图2 径向疲劳试验机
径向载荷按照下式确定:
Fr=FK
(1)
式中:Fr为径向载荷;F为车轮或主机厂规定的最大垂直静负荷或车轮额定负荷;K为试验强化系数,当K取2.0时,寿命应不小于100万次,当K取2.25时,寿命应不小于50万次[6]。
文中采用一铝车轮进行试验和分析,径向试验载荷为14.945 kN,要求循环次数为150万次。试验后的轮毂和试验参数如图3所示,轮毂表面无可见裂纹,轮胎胎压和螺栓扭矩衰减低于5%,满足性能要求。

图3 试验后的轮毂和试验参数
2 车轮径向疲劳有限元分析流程
车轮径向受力有限元分析过程中,车轮与工装通过螺栓进行连接,预紧力和接触对车轮的应力分布影响不大,通常可忽略;轮胎充气压力对车轮的应力分布影响也非常小,也可忽略;由于轮胎结构复杂,而且材料是非线性橡胶材料,受载时发生大变形,所以进行完整轮胎建模工作量非常大,分析中省略轮胎,径向载荷按照一定的分布方式直接施加到车轮。
在HyperMesh中创建车轮台架径向疲劳计算有限元模型时,首先导入车轮的几何模型,根据车轮的几何特点确定车轮和轮胎座的分割方法,分割好后进行有限元网格划分,根据车轮的安装状态进行约束设置,根据每一个受力方向创建局部坐标系进行载荷加载,其正常操作流程如图4和图5所示。这些流程人工操作步骤复杂,操作项数量多,容易产生误操作。
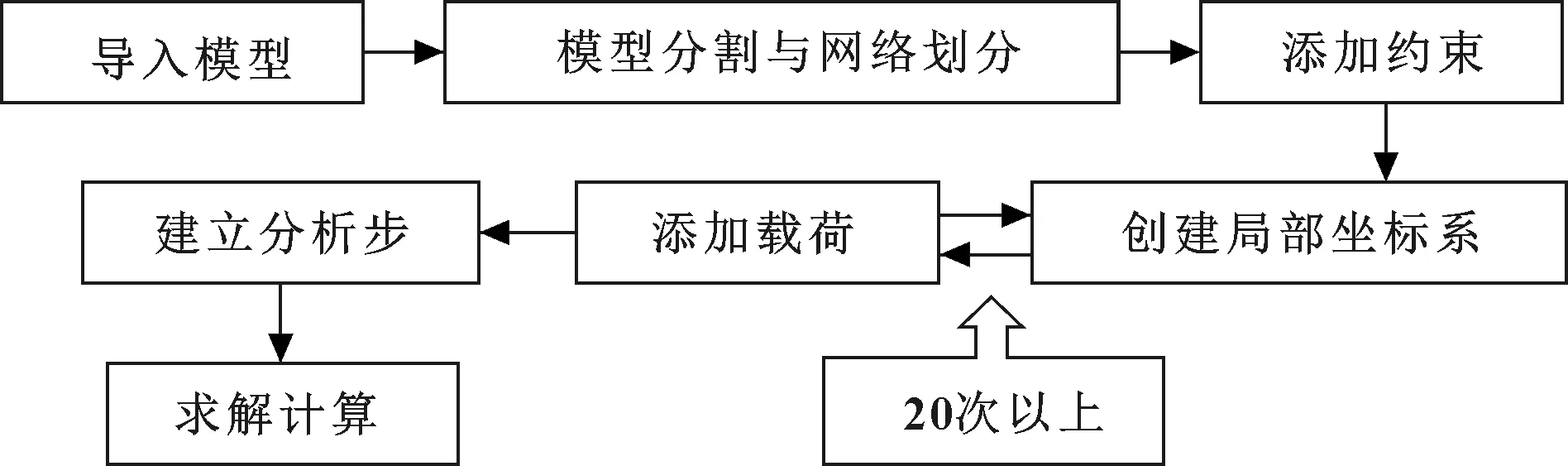
图4 车轮径向疲劳分析流程图(一)
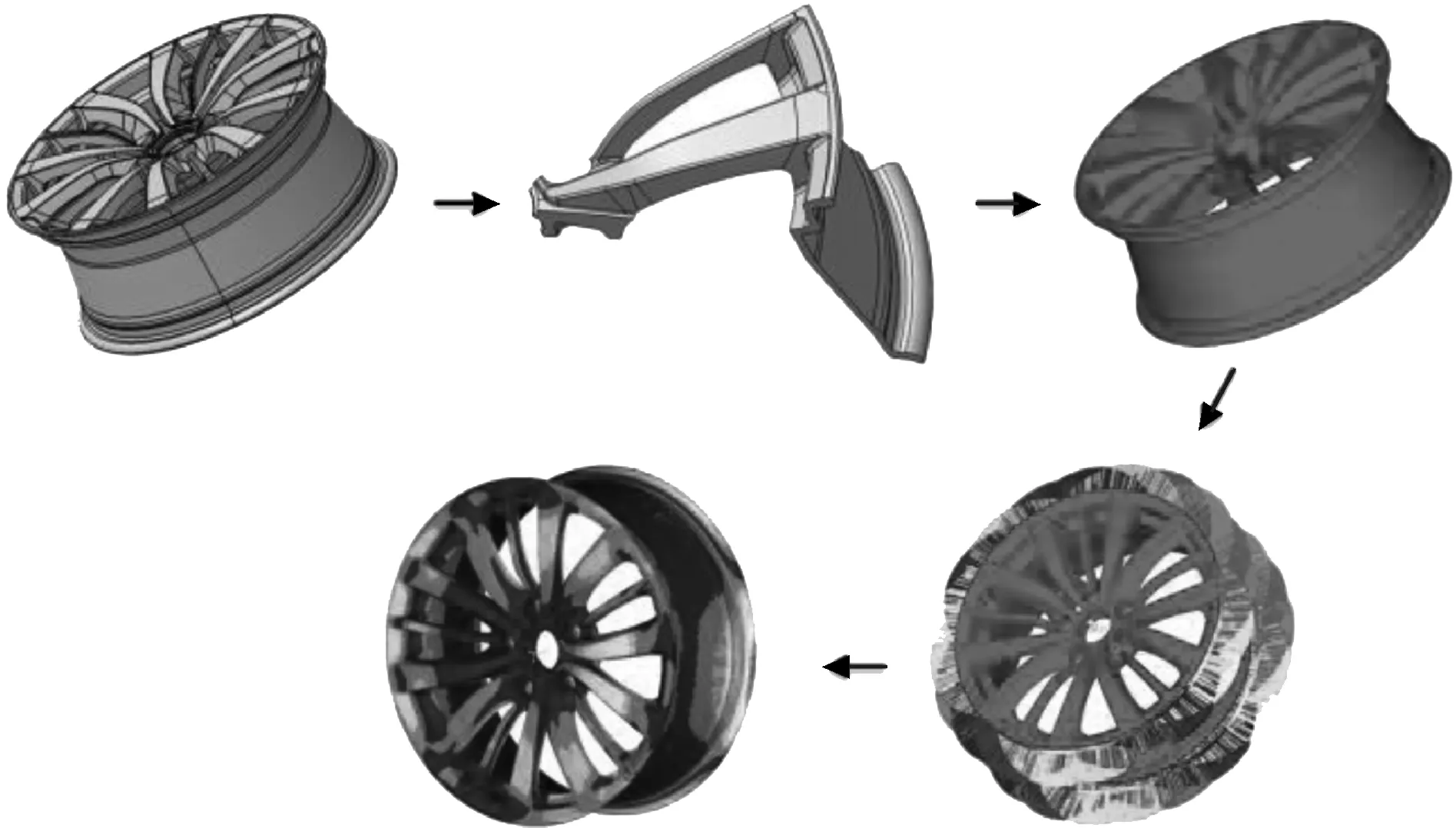
图5 车轮径向疲劳分析流程图(二)
3 轮胎座分布力计算
车轮承受径向载荷时,只有与台架转鼓接触区域的部分橡胶发生大变形,按照经验该区域在外力作用下变形(0°~72°),并且分布方式呈余弦形式,中间高,两侧逐渐减小至零,方向沿着轮子径向。
计算时,以车轮中心为原点建立局部柱坐标系,R轴为车轮径向。在R轴两侧72°(左右各36°)范围内施加分布力,加载区域为轮辋内外胎圈座。加载载荷计算公式如式(2)—(3)所示。分布力在中间位置大,向两侧逐渐减小至零,方向沿着车轮径向指向轮心,如图6所示。
(2)
(3)
式中:R为轮胎座半径;W为径向疲劳试验载荷的一半;b为轮胎座受力宽度;Wr为与轴线成θ角处的车轮径向分布力;W0为最大径向分布力;θ0为径向载荷作用范围的最大偏角,即36°。

图6 轮胎座分布力示意图
4 自动化加载流程实现
针对添加径向载荷过程中的载荷分布非线性,加载区域繁多和多个加载工况,需要特别设计一款自动化程序,该程序应当具有选取元素少,设置和操作方便的特点,因此可将加载流程进行模块化分解。正常思路是每一个局部柱坐标系对应加载一系列载荷,但是为了操作方便不可能在程序中多次创建柱坐标系,因此可以改变载荷公式参数进行更改加载角度,而此时单独采用一个HyperMesh中的柱坐标系是不能完成360°依次加载的,因此在确定好该坐标系的加载有效角度范围对加载区进行分块,之后旋转坐标系依次进行分区加载,最终完成整个加载过程。该流程图如图7所示。
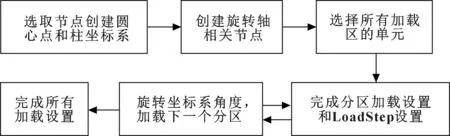
图7 自动化加载算法
程序中编写了不同的分块程序实现分区内的载荷加载,使其通过循环的方式减少代码数量。下面的程序段会实现分区内循环加载。
for {set i 0} {$i<5} {incr i} {
*createmark loadcols 1 $loadcols_name
*collectorcreate loadcols "$loadcols_name" ""/ [expr int(64*(rand())) + 1]
eval *createmark elements 1 $elements
*pressuresonentity_function elements 1 1 0 0 0/ 1 30 1 0 0 0 "3.9 *cos(2.5*(y-$i*0.31415926/
-3*0.31415926))" [hm_entitymaxid systs]
set x_C_1 30
*createmark loads 1 "by box" $x_C_1 $y_C_1/ $z_C_1 $x_C_2 $y_C_2 $z_C_2
[hm_entitymaxidsysts] outside 0 0 0
}
下面为坐标系旋转代码,实现旋转改变分区。
set origin_node_cord [hm_nodevalue $origin/_node]
set origin_cor [lindex $origin_node_cord 0]
set ori_1 [split $origin_cor " "]
set ori_1_x [lindex $ori_1 0]
set ori_1_y [lindex $ori_1 1]
set ori_1_z [lindex $ori_1 2]
*createnode 0 0 50 [hm_entitymaxid systs] 0 0
set orientation_node [hm_entitymaxid nodes]
*createmark systems 1 [hm_entitymaxid systs]
*createplane 1 $ori_1_x $ori_1_y $ori_1_z/ $ori_2_x $ori_2_y $ori_2_z
*rotatemark systems 1 1 90
将写好的存储程序转成*.tcl格式,通过userpage.mac的创建按钮功能将程序搭载到HyperMesh中。在userpage.mac中可通过下面的代码进行按钮设置。
*createbutton(5,"按钮名称",0,0,10,按钮颜/色,"",EvalTclScript,"D:/TclTools/按钮名称.tcl")
*beginmacro("EvalTclScript")
*evaltclscript($1,0)
*endmacro()
为了方便不同直径的轮胎座宽度,特设定相应的设置界面,该界面可输入内容包括轮胎座直径、轮胎座宽度和加载所需的径向力,如图8所示,设定好之后单击添加径向力按钮即可进入主程序执行模块。

图8 程序设置界面
5 铝车轮径向疲劳计算
以与试验相同的车轮数模作为分析对象,在HyperMesh软件中对车轮进行加载区划分和网格划分,设置材料属性,添加连接单元和约束后,采用自动化程序对车轮加载和计算,图9和图10分别为车轮在0°和144°位置的计算结果云图,其中车轮上的最大应力发生位置均在轮毂内缘外圈上,轮子使用材料为A356,材料特性为:弹性模量78 GPa,泊松比0.33,屈服强度180 MPa,抗拉强度260 MPa,应力计算结果均未超过材料屈服强度。
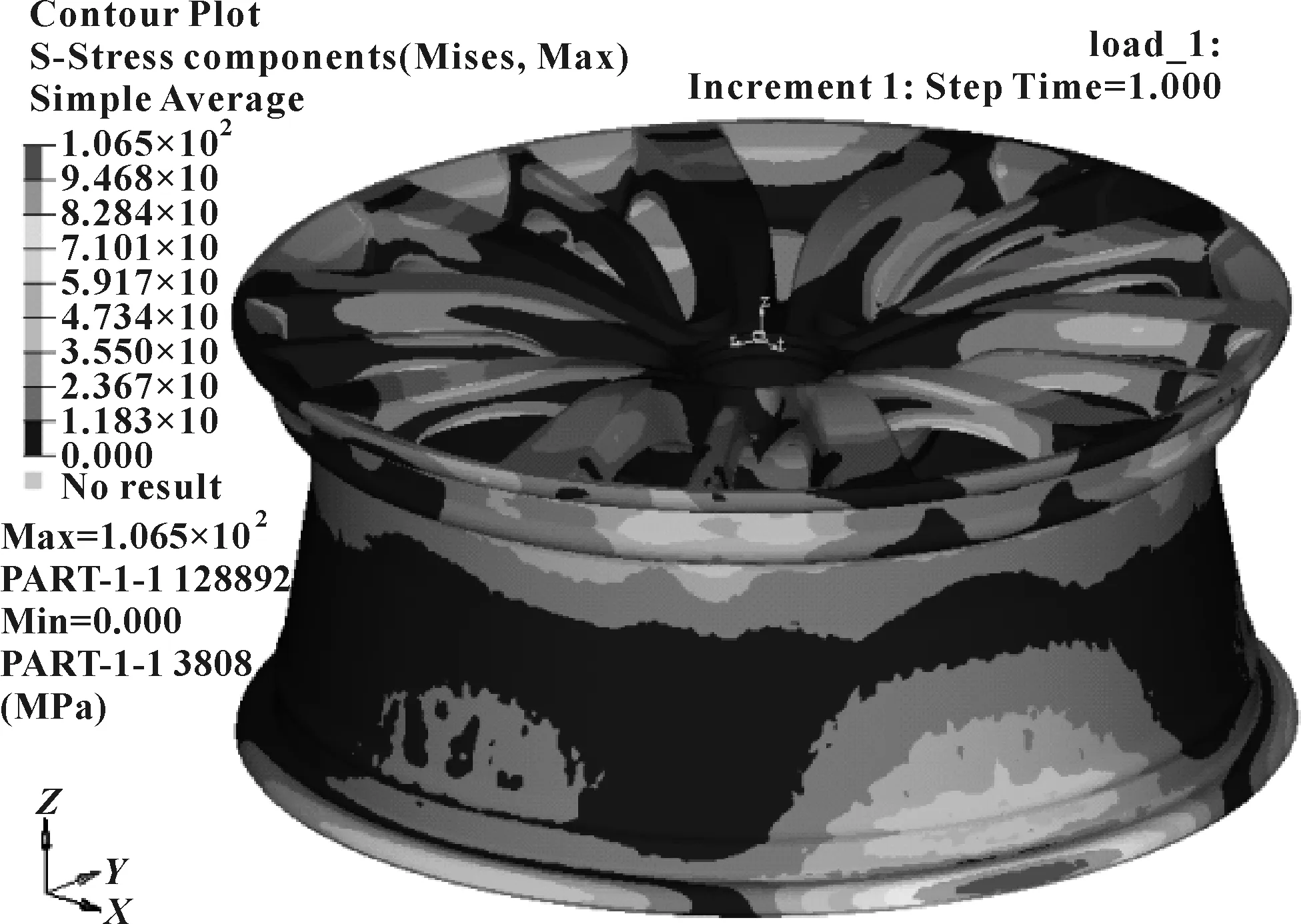
图9 车轮在0°位置的计算结果云图
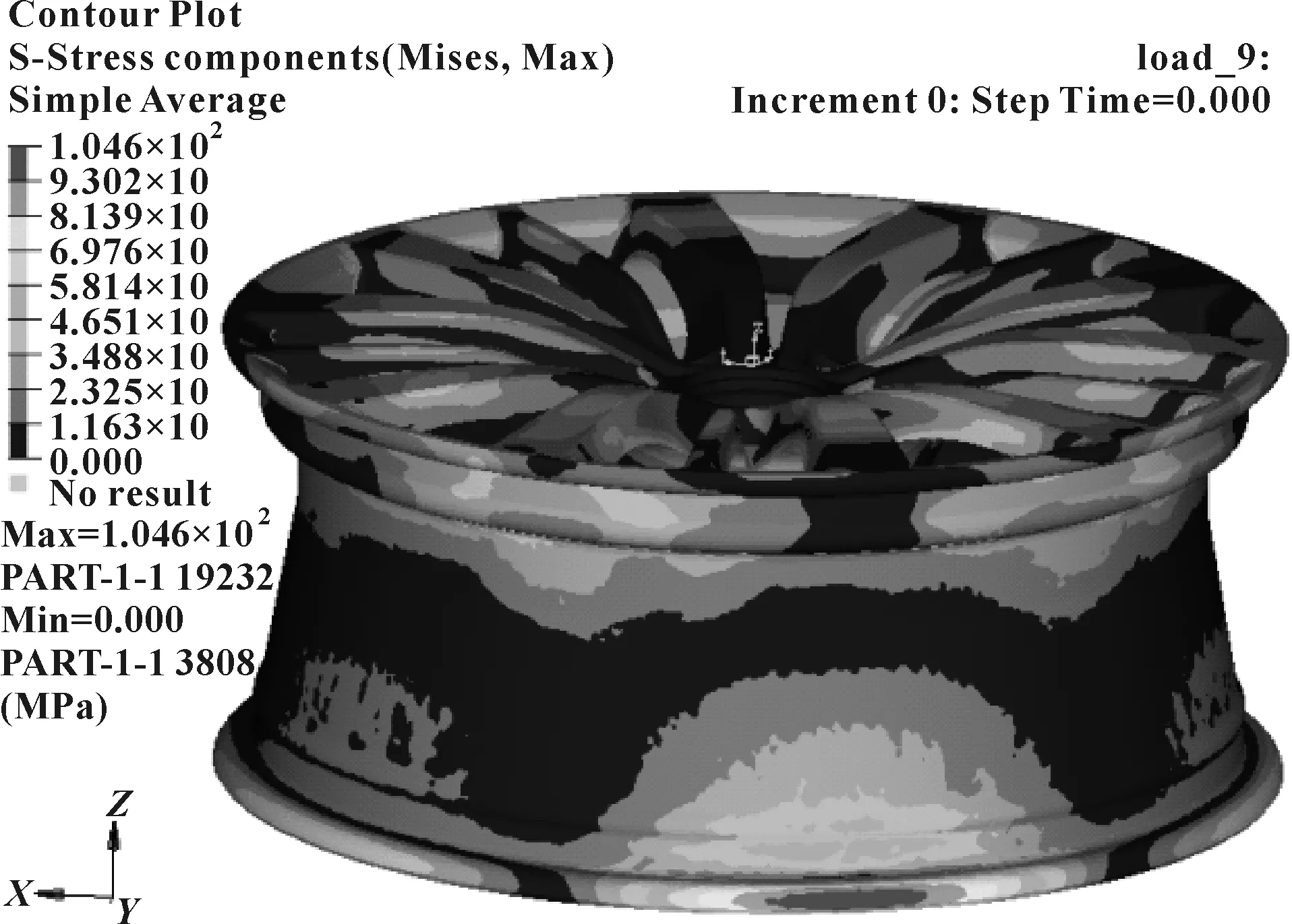
图10 车轮在144°位置的计算结果云图
将计算结果文件导入疲劳软件Femfat中的TransMax模块内进行疲劳分析,根据材料的抗拉和屈服极限生成材料应力寿命曲线,如图11所示。
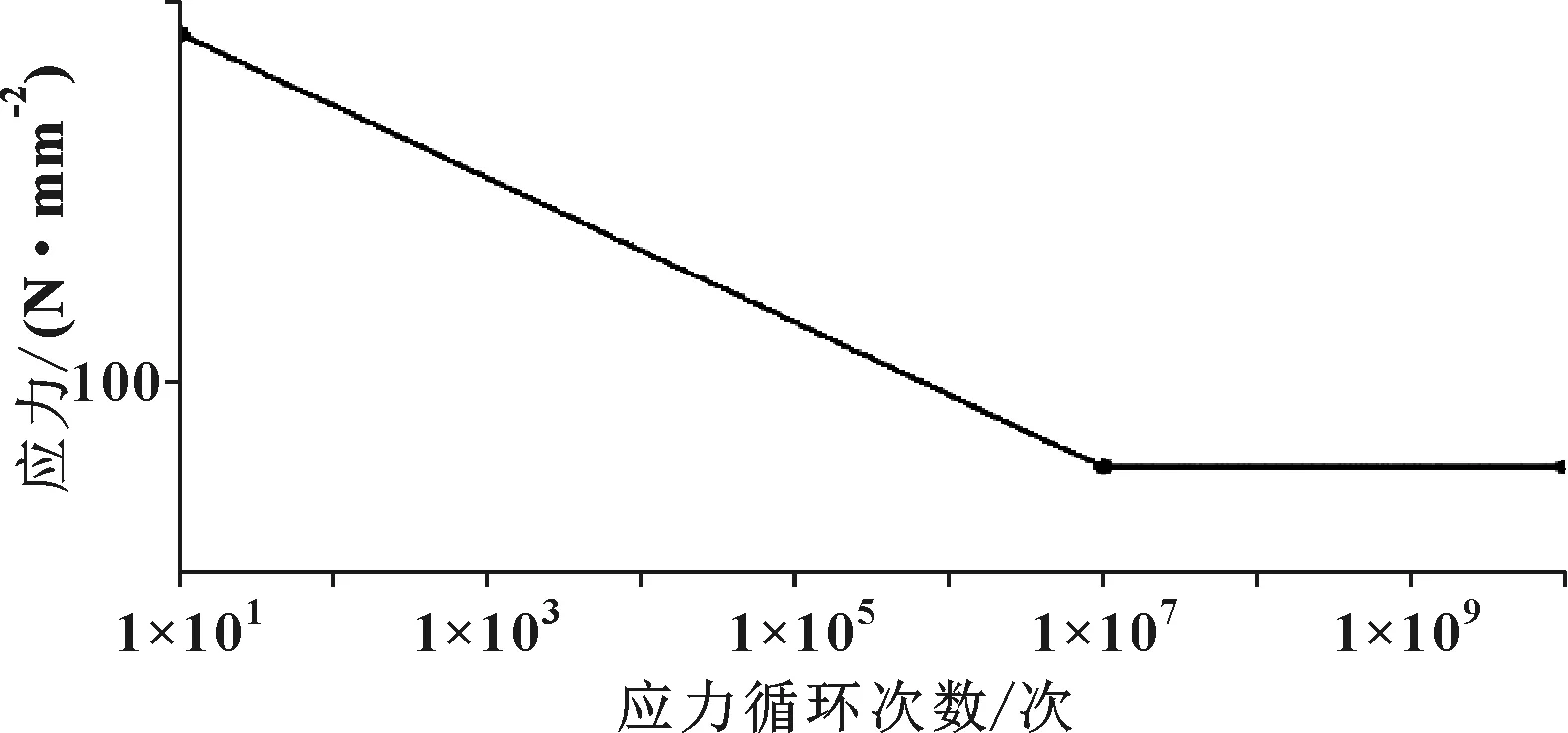
图11 材料的S-N曲线
在软件中设置好疲劳相关的参数后,计算出的寿命云图如图12所示,其中最低寿命为4.37×109次,远高于目标要求的1.5×106次,寿命差距过大是因为软件会根据部件的形状特征和应力修正从而生成部件的S-N曲线,因此该计算是有效的,如图13所示,图中线条1为部件的S-N曲线。

图12 疲劳计算结果云图
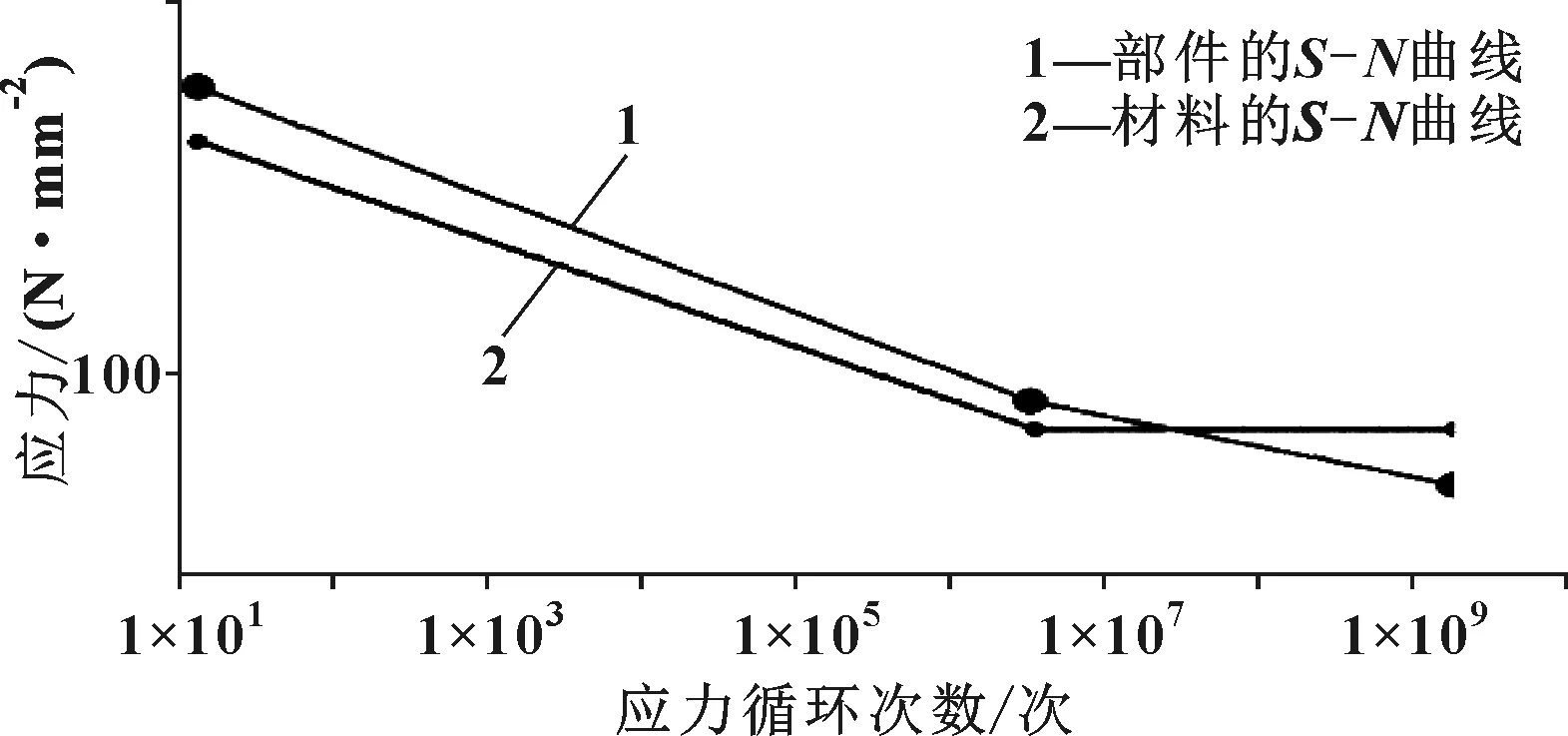
图13 材料和部件的S-N曲线
6 结论
经过实践验证,自动化流程使得加载设置过程的时间缩短了98%,同时缩短了整体建模的时间,提高了工作效率,减少了工作中人为操作产生的失误。采用Femfat软件进行轮毂疲劳计算能够方便地设置与疲劳相关的各项因子,还能够计算出部件局部的S-N曲线,使疲劳寿命预测得更加准确。
