Comparison of single-neutral-atom qubit between in bright trap and in dark trap∗
2019-02-25YaLiTian田亚莉ZhiHuiWang王志辉PengFeiYang杨鹏飞PengFeiZhang张鹏飞GangLi李刚andTianCaiZhang张天才
Ya-Li Tian(田亚莉),Zhi-Hui Wang(王志辉),Peng-Fei Yang(杨鹏飞),Peng-Fei Zhang(张鹏飞),2,Gang Li(李刚),2,†,and Tian-Cai Zhang(张天才),2,‡
1 State Key Laboratory of Quantum Optics and Quantum Optics Devices,and Institute of Opto-Electronics,Shanxi University,Taiyuan 030006,China
2 Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
Keywords:single qubit,laser trapping,coherence time
1.Introduction
Quantum bits(qubits)encoded in single neutral atoms are among the most promising candidates to realize quantum information processing.[1,2]Qubit is usually encoded in the hyper fine or Zeeman states of single atom.Thus,long lived single atom with long coherence time will benefit the processing of quantum information.In a real experiment,a single neutral atom is usually confined in a micro-sized far off-resonant optical trap(FORT).[3-9]To prolong the storage time of single atom in FORT,the ultra-low pressure vacuum is requested to suppress the collision with the background atoms.Periodic cooling is adopted in the red-detuned trap to recool the atom when it is heated by scattering the trap photons.[10]The coherence time of a confined atom is mainly limited by the inhomogeneous mechanism due to the state energy fluctuations associated with the movement of the atom in FORT.[11]The trap potential of a FORT is formed by the locally distributed ac Stark energy shift associated with the intensity distribution,thus there is a differential Stark shift between the two qubit states due to unequal polarizabilities.Then,the movement of the atom will induce the energy distance between the two states to fluctuate,and thus dephase the quantum state.To eliminate this inhomogeneous dephasing,researchers have been searching for a trap with magic conditions where the differential ac-Stark shifts between two interested atomic states are independent of the intensity distribution of the trap beam.[12-14]Although the magic condition can dramatically extend the dephasing time,it can only be found for some special quantum states and it is still a challenge to search for the magic condition for many atomic species.Without considering the magic conditions,the dark trap(blue-detuned trap)confines atom in its intensity minima with even zero excitation and in principle is expected to possess longer storage time and coherence time than bright trap(red-detuned trap)for all the atomic species and states.In this paper,we experimentally compare the qubits encoded in “clock states”of single cesium atom confined in 1064-nm bright trap and 780-nm dark trap,respectively,under almost the same trap depth.This provides a direct proof of superiority of dark trap over bright trap.
2.Structures of trap and single atom loading
In our experiment,as shown in Fig.1(a),the bright trap is formed by deeply focusing a 1064-nm laser beam with a beam diameter 12 mm through a high numerical aperture lens group(NA=0.29 and f=36 mm).The waist size of the trap is 2.0µm,and the corresponding frequency detuning to cesium D1(D2)line is about-53 THz(-70 THz).Therefore,by using 16-mW trap power,we can obtain a trap potential of-kB×0.63 mK,where kBis the Boltzmann constant.The dark trap is formed by shining two parallel donut 780-nm laser beams with orthogonal polarizations through another high numericalaperture lensgroup(NA=0.4 and f=22.9 mm).The experimental setup is described in Fig.1(b).The two beams will intersect with each other at the lens focus where the beam waist is located simultaneously.The donut beam is produced by sending a Gaussian beam with a beam size of 1.83 mm through a spiral phase plate(VL-209-M-Y-A,HOLO/OR),and the beam is subsequently separated by a calcite beam displacer into two parallel beams with orthogonal polarizations.The distance between two donut beams is 4 mm.The trap profile is measured at focus and is depicted in Fig.2.We can see that the crossed donut beams produce a dark spot surrounded by high intensity.[15]Since the frequency detuning of 780-nm trap beam to Cesium D1(D2)line is about 49 THz(33 THz),the high light intensity will form a potential barrier and make the dark spot a trap.This bottle trap has a size of about 2.0µm along the radial directions and 11µm along the axial direction.By using 190 mW of trap power the minimum barrier height is about kB×0.63 mK.
To load the atom from the precooled atom sample,both of the traps are superposed with the atom ensembles in the magneto-optical trap(MOT).The scattered photon by trapped atom is collected by the same objective lens groups and is finally fed to single photon detectors(Figs.1(a)and 1(b)).[6]

Fig.1.Experimental setups of bright trap(a)and dark trap(b).A TEM00 Gaussian beam or two orthogonal polarized donut beams are tightly focused beam by a high numerical aperture lens(NA=0.29 for bright trap and NA=0.4 for dark trap)to produce the bright or dark trap.The traps overlap exactly with MOT to load single atom from precooled atomic samples.Fluorescence photons scattered by trapped atom are collected by the same lens group and separated from the FORT beam path by a dichromic mirror and finally feed to SPCM.HWP:half wave plate;NA:numerical aperture;HR:high reflection;SPCM:single photon counting module;PC:personal computer.

Fig.2.(a)Measured intensity distribution of the dark trap by a CCD camera in x-y plane at positions of z=2µm,12µm,and 22µm.(b)and(c)Reconstructed intensity distribution in x-z and y-z planes.
Since the red trap has a negative potential,atoms can be attracted to the trap center.So the red trap does not need to be switched off during the atom loading phase.The trap volume is a region where the trap potential on the border is equal to the kinetic energy of the cold atoms kB∗TMOT.[3]Atoms that have already been in this region can be effectively trapped.The atomic ensemble in our MOT has a temperature of 15µK which gives a red trap volume of 681µm3.The atoms loaded into the trap finally accumulate in the trap bottom where the light assistant 2-atom collision by the red detuned MOT beam pushes atoms out of trap two by two,and finally only zero or one atom is left.[16]Figure 3(a)shows the single atom signal loaded to the FORT,and Fig.3(b)displays the histogram which gives a single atom loading probability around 60%,which is a little higher than the theoretical value given in Refs.[16]and[17].The loading probability could be further increased by using light assistant collision induced by blue-detuned beam or feedback technique.[18-20]
In contrast,the blue bottle trap can only trap the atom already within the trap volume which is set up by the high trap barrier.The atom outside the trap region cannot enter into the trap due to low kinetic energy.Thus,our 780-nm bottle trap has a volume of 184µm3.The trap needs to be switched off at the beginning,and after the atom samples in MOT is ready,the FORT is then switched on again to trap the atom.In order to obtain a considerable loading probability the density of the atom cloud needs to be as high as possible.Once two or more atoms have been trapped,the light assistant two-atom collision will finally leave zero or one atom as the scenario in the red trap.Figure 3(c)shows the single atoms’signals in dark trap.From the histogram shown in Fig.3(d)we obtain a lower loading efficiency of 40%in the dark trap than in the red trap due to the low atom density in our experiment.
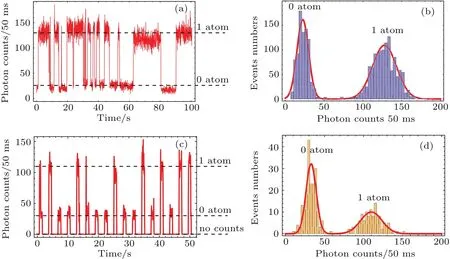
Fig.3.Typical signal from single atoms trapped in(a)bright and(c)dark trap,and((b)and(d))their corresponding histograms.
3.Atom heating in traps and atom storage time
For an ideal conservative trap,the atom loss due to the parametric heating of the fluctuation of the trap and the storage time of trapped atoms are determined only by collision from background atoms in the vacuum chamber.The storage time is determined by the vacuum pressure through[21]

where m is the mass of trapped atom,kBis the Boltzmann constant,Tbis the environment temperature,σ is the atomatom collisional cross section,and Pbis the background pressure.In both of our experiments with bright and dark traps,the background temperature is 300 K and our vacuum pressure is about 2.66×10-9Pa.Considering the cesium-cesium collisional cross section σ ∼ 3.14×10-13cm2a single atom storage time of about 200 s for both traps is expected in theory.The actual measurements of storage time for both of the traps are shown in Fig.4.We can see that the survival probability of atom in the bright trap is in a strange shape and the overall storage time is much shorter than in dark trap because of the parametric heating of the trap beam intensity noise.For the blue-detuned trap the atom is trapped in the intensity minima,so the parametric heating is suppressed.If the light intensity in the trap center is low enough the atom storage time is then mainly limited by the background collisions.Figure 4(b)showsour measurementin the 780-nm bottle trap and the atom survival lifetime is 118 s,which is still shorter than the theoretical expectation due to the residue parametric heating.
For those atoms confined in the intensity maxima in the bright trap,parametric heating is the dominant reason for atom loss.According to Ref.[22]the change of average energy 〈E〉of atom in bright trap can be expressed as

where Γεis the heating constant which is related to the intensity noise of trap beam around the sidebands with twice the atom’s oscillation frequency.The energy of the trapped atom increases exponentially due to the parametric heating.Once the atom energy exceeds the trap potential,the atom will escape from the trap.
For an atom with temperature T the energy distribution obeys the Boltzmann statistics

There is a certain probability with which the atom energy exceeds the trap potential U and this part of atoms will escape out of the trap.The Boltzmann distribution is then truncated and the mean energy of the remaining atom will decrease due to the loss of the high-energy atoms.If we take this effective cooling effect into account,then equation(2)becomes,
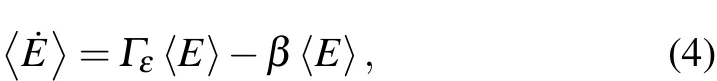
where β = Δ〈E〉/〈E〉=(〈E〉-〈E′〉)/〈E〉is the effective cooling rate.To calculate β we need to know the average energy 〈E′〉of the trapped atom after the high-energy atoms has been lost.This is given by[22]
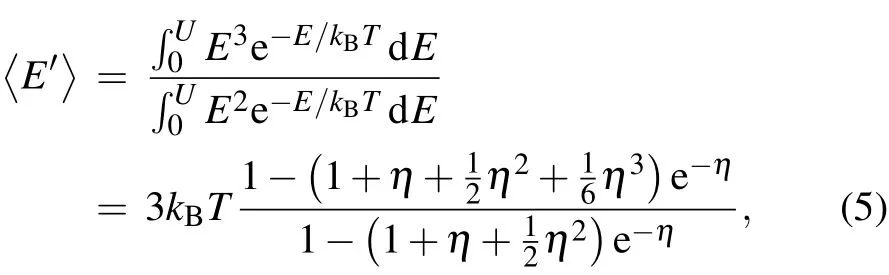
where η=U/kBT.Thus

Here we have used 〈E〉=3kBT in a three-dimensional trap.
The dynamic of atom’s survival probability P then obeys
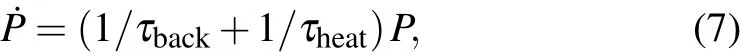
where 1/τbackis the loss rate due to the background collision and

is the atom loss rate due to parametric heating.From Eqs.(4)and(7)we can obtain the dependence of temperature and atom survival probability on storage time.The experimental data of the survival probability and temperature versus storage time,the corresponding theoretical fittings are shown in Fig.4(a).The temperature is measured by release and recapture method.[23]We can see that the atom temperature increases as storage time is extended.The temperature increases exponentially at the beginning of storage as indicated by Eq.(2),when the corresponding Boltzmann distribution of atom kinetic energy mainly resides below the trap depth and the atom loss due to the parametric heating can be neglected.In this region,the atom loss is mainly caused by the collisions of the trapped atoms with the background atoms.As the storage time increases,the temperature of atom goes up further and the truncation of Boltzmann distribution cannot be omitted.The cooling effect then begins to work and the increase of the atom temperature slows down.The process is strictly described by Eqs.(4)and(3).The atom loss is then dominated by the parametric heating.The overall storage time is measured to be 27.8 s.This storage time can be improved by cooling the atom periodically.The blue data points in Fig.4(a)are the results with 5-ms cooling in every 10 seconds after the atom has been trapped in the red trap.The storage time is then prolonged to 79.3 s.

Fig.4.Plots of storage time of single atom in(a)bright trap and(b)dark trap.Red points and blue points in panel(a)are data with and without periodic cooling,respectively.The red and blue curve are the theoretical fittings,which give single atom lifetime of 27.8±1.2 s without periodic cooling and 79.3±5.6 s with periodic cooling,respectively.The inset in panel(a)shows temperature of the atom versus storage time and the fitting.The measurement of single atom lifetime in dark trap is shown in panel(b),which gives a life time of 117.7±10.6 s.The data points are obtained by using the statistic over more than 100 atom samples and the range of error bars shown here is±σ,where σ denotes standard deviation.
4.Qubit decoherence
A single atom with a long storage time can be used as carrier of single qubit for quantum information processing and quantum computation.The dephasing time of the qubit is the most important factor for these applications.The coherence time of the qubit encoded in single trapped neutral atom is mainly limited by the variation of the differential ac Stark shift between the two encoded states when atom oscillates in the trap.[11]This dephasing mechanism is usually classified as an inhomogeneous dephasing process.In our experiment,the qubit is encoded in the cesium “clock states”with the notations|0〉≡ |F=4,mF=0〉and|1〉≡ |F=3,mF=0〉.The qubit is firstly initialized to|0〉and a resonant microwave with a frequency of 9.2 GHz is used to drive the state to rotate.By using a standard Ramsey’s interferometer the qubit coherence time T2can be precisely measured.Figure 5 shows the interference signal on the time scale with atom trapped in the bright trap(Fig.5(a))and dark trap(Fig.5(b))with temperature T=15µK,respectively.In the bright trap,=4.9 ms,which is consistent with a theoretical dephasing time[11]
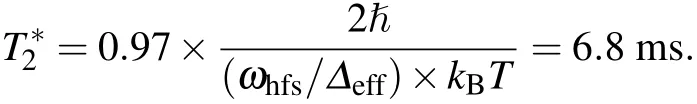
Here,ωhfsis the ground-state hyper fine splitting,Δeffis the effective detuning with D1 and D2 lines.By comparison,the dephasing time is extended to 10.1 ms in the dark trap,which is due to the low trap light and thus lower inhomogeneous dephasing than that of bright trap.In addition,the dephasing time is still limited mainly by the motion of the atoms.When the atoms are cooled to their vibrational ground state of the trap potential,it is possible to obtain a longer coherence time.

Fig.5.Evolution of Ramsey fringe amplitude with time delay between two π/2 pulses in(a)bright trap and(b)dark trap.Data points are obtained by statistic of about 100 atom samples and range of error bars shown here is±σ,where σ is standard deviation.Red curve denotes theoretical fitting of cosine function with exponential decay,which gives a single qubit coherence time of 4.9±1.2 ms in bright trap and 10.1±1.0 ms in the dark trap.
5.Conclusions and perspectives
In this work,we have experimentally compared the qubits encoded in the “clock states”of single cesium atom confined eitherin a 1064-nm bright trap or in a 780-nm dark trap:which possess almost the same trap depth.Due to less heating effect,the atom lifetime can be extended to hundred seconds in the dark trap,which is longer than that in the bright trap.Lifetime is primarily limited by collisions of the trapped atoms with the background hot atoms.The coherence time of single qubit states in the dark trap is more than twice as long in the bright trap.Recently,the magic condition for qubits encoded in hyper fine state of an optically trapped atom has been found theoretically and experimentally.In the magic trap,the inhomogeneous dephasing can be suppressed in the dark trap and the coherence time for the clock state can be extended to hundreds of ms.[24]Of course,to realize the magic condition,the trap beam polarization,bias field,and other parameters of the trap need to be accurately controlled.For a relatively simple trap such as the setups shown here,the dark trap has obviously more advantages for quantum information processing than the bright trap.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Physics of quantum coherence in spin systems∗
- Recent progress of infrared photodetectors based on lead chalcogenide colloidal quantum dots∗
- Progress in quantum well and quantum cascade infrared photodetectors in SITP∗
- Recent advances in Ga-based solar-blind photodetectors∗
- Development of long-wavelength infrared detector and its space-based application requirements∗
- Transition of photoconductive and photovoltaic operation modes in amorphous Ga2O3-based solar-blind detectors tuned by oxygen vacancies∗
