基于EFEN-SP3方法的pin-by-pin中子动力学计算方法研究

谢伟华，曹良志，李云召

(西安交通大学 核科学与技术学院，陕西 西安 710049)

pin-by-pin的压水堆三维瞬态计算可直接给出安全分析所需的单棒功率密度分布而不需要引入组件均匀化近似和精细功率重构带来的误差[1]。但pin-by-pin中子动力学计算以栅元为最大计算网格，一方面使中子扩散计算的假设不再满足，另一方面计算量和存储量也都增加了几个量级。本文在西安交通大学自主研发的压水堆堆芯燃料管理计算程序系统NECP-Bamboo2.0[2]的基础上，采用全隐式向后差分方法离散SP3中子动力学方程组的时间项，采用指数函数展开节块-SP3(EFEN-SP3)方法[3]求解含裂变介质的固定源方程。其中，由于EFEN中采用的平源近似假设与缓发中子先驱核浓度计算时认为的缓发中子先驱核浓度形状和中子通量密度形状相同不兼容，造成计算误差会随时间步累积。因此，本文采用高阶源展开的指数函数展开方法[4]抑制计算偏差随时间步不断增加的趋势，并采用一系列加速技术对EFEN-SP3的固定源问题求解过程进行加速。

1 理论模型

三维多群时空SP3中子动力学方程组经全隐式向后差分离散后可得tn+1时刻的固定源方程组[5]：

(1)

其中：

(2)

相应的缓发中子先驱核浓度方程为：

(3)

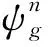
若Pn为第n阶勒让德多项式、hi为节块在i方向上的长度(cm)，将源项在x、y、z3个方向上用勒让德多项式展开：

(4)

其中：sn为勒让德多项式展开系数；N为多项式展开最大阶数。

基于EFEN-SP3方法，可得到中子通量密度解析解[4]为：

ψ(x,y,z)=Cu+eκx+Cu-e-κx+Cv+eκy+

Cv-e-κy+Cw+eκz+Cw-e-κz+ψ0+

(5)

将其近似为多项式形式，可得：

(6)

其中：Cu±、Cv±、Cw±分别为x、y、z3个坐标系上的展开系数；κ为自定义系数，由总截面和扩散系数求得。

本文采用3种加速方法对EFEN-SP3的固定源问题求解过程进行加速，具体包括Ks因子[6]、LW外推[7]和粗网再平衡[8]。

2 数值验证与分析

本文基于建立的pin-by-pin中子动力学计算方法，研发了相应的计算程序EFEN-K，并对高阶源展开方法和加速方法进行了验证与分析。

2.1 高阶源展开方法验证

二维TWIGL扩散基准题是一简化的两群瞬态问题，堆芯是由3个燃料区组成的边长为160 cm的正方形，组件尺寸为8 cm×8 cm，详细的堆芯几何布置示于图1，材料的截面参数参考文献[9]。瞬态过程由燃料区1的热群宏观吸收截面Σa，2发生如下线性变化引起：

(7)

图1 二维TWIGL基准题几何布置Fig.1 Geometric distribution of 2D TWIGL benchmark

设堆芯的初始归一化功率为1.0，分别以10-2、10-3、10-4和10-5s的时间步长模拟计算0.5 s的瞬态过程。

平源近似下的功率曲线如图2a所示，参考Bamboo-Transient[10]的相对偏差曲线如图2b所示。由图2可看出：计算结果不随时间步长的缩小而收敛，在时间步长取10-5s时，相对偏差开始显著增大。高阶源展开下的功率曲线如图3a所示，参考Bamboo-Transient的相对偏差曲线如图3b所示。由图3可看出：计算结果随时间步长的缩小而逐渐收敛，并稳定在0.35%左右，主要是SP3方法与扩散近似之间的方法差异带来的偏差。

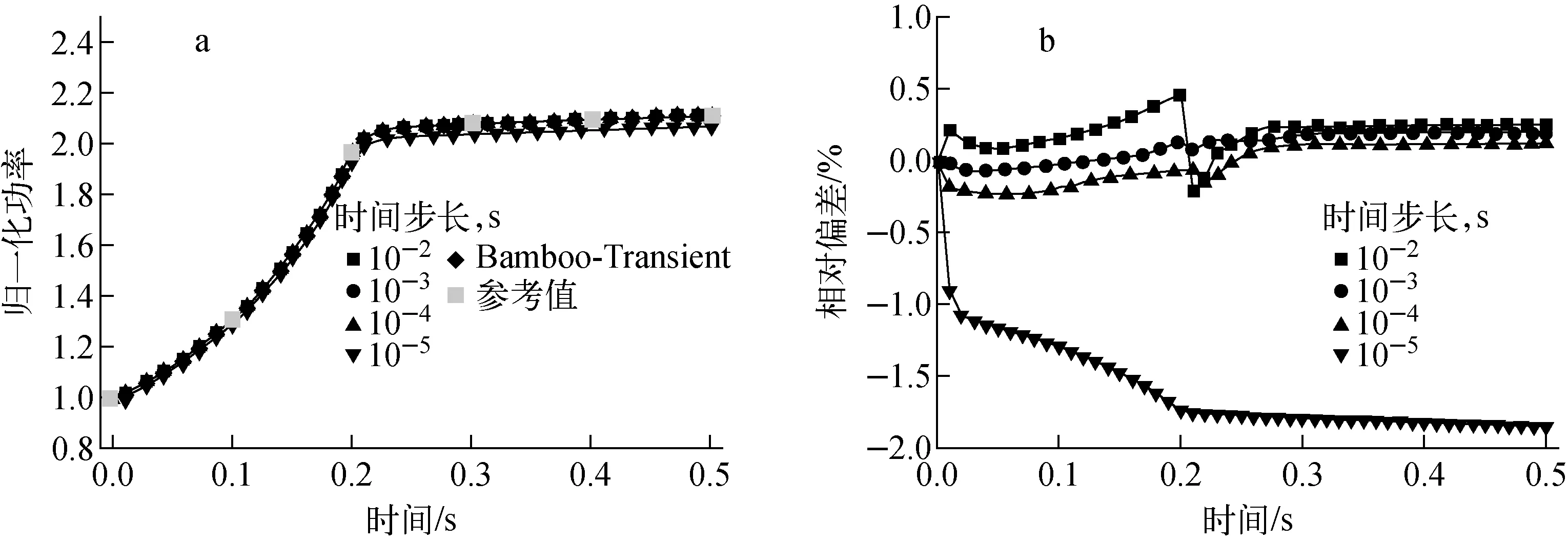
图2 平源近似下的归一化功率和功率相对偏差Fig.2 Normalization power and relative deviation of power with flat-source approximation

图3 高阶源展开下的归一化功率和功率相对偏差Fig.3 Normalization power and relative deviation of power with high-order source expansion

2.2 加速方法验证

参考VERA基准题[11]设计压水堆三维单组件pin-by-pin算例，其径向右下1/8几何布置如图4所示。整个组件包含1个裂变室、24个导向管与264根燃料棒，栅元间距为1.26 cm，最外层栅元包含0.04 cm的水隙，轴向半组件高度为1 250 cm，上部有20 cm的反射层，之外是真空边界条件，下部采用全反射边界条件。4群截面参数列于表1，动力学参数列于表2。瞬态过程由导向管材料的总截面在初始时刻发生如下阶跃变化引起，近似模拟0.02 s内控制棒插入过程。

图4 加速方法验证算例径向1/8示意图Fig.4 Sketch of 1/8 verification case for acceleration method

(8)

采用4种不同方案进行计算：1) 不加速；2) Ks因子加速；3) Ks因子和LW外推(Ks+LW)加速；4) Ks因子、LW外推和粗网再平衡(Ks+LW+CM)加速。细网计算的网格划分是径向每个栅元1个计算网格，轴向网格为5.0 cm。粗网再平衡的网格合并方案为：径向x方向6个网格和y方向6个网格与z方向5个网格合并成1个网格。

表1 加速方法验证算例单组件截面参数Table 1 Cross section of fuel rod in verification case for acceleration method

续表1

表2 加速方法验证算例动力学参数Table 2 Kinetics parameter of verification case for acceleration method

注：β=2.133 33×10-4pcm，λ=0.08 s-1

针对4种方案的计算结果比较如图5a所示，以无加速下的结果为参考解，另外3种方案结果的相对偏差如图5b所示。由图5可见，加速方法对结果影响很小，可忽略。对4种方案的计算总时间进行统计，结果列于表3，可看出：Ks加速可取得47.6倍左右的加速；LW外推在此基础上可获得1.99倍的加速；粗网再平衡可在此基础上获得1.42倍的加速；3种加速技术共可实现134.9倍的加速。

图5 4种方案SP3计算的归一化功率与相对偏差Fig.5 Normalization power and relative deviation of power of SP3 calculation with 4 cases

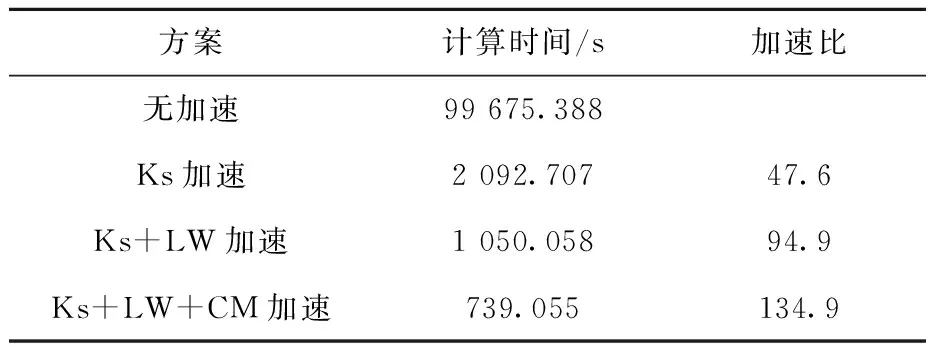
方案计算时间/s加速比无加速99 675.388Ks加速2 092.70747.6Ks+LW加速1 050.05894.9Ks+LW+CM加速739.055134.9

2.3 三维多组件问题

该算例参照C5G7-TD基准题[12]，径向几何如图6所示，由两个UOX组件与两个MOX组件相隔布置而成，四周为全反射边界，活性区高度为42.68 cm，顶部为21.34 cm的轴向反射层，外为真空边界条件，底部无反射层，为全反射边界条件。栅元均匀化少群常数由压水堆栅格计算程序Bamboo-Lattice2.0提供。瞬态过程中，所有材料的总截面与散射截面的线性变化，用于模拟硼浓度的变化。具体为在0～1 s内所有能群的总截面线性增加0.1%，所有能群的散射截面线性减少0.1%；在1～2 s内截面线性恢复初始截面。瞬态模拟过程为3 s。

图6 pin-by-pin问题径向几何布置Fig.6 Radial configuration of pin-by-pin problem

EFEN-K采用SP3近似，计算时径向网格为1个栅元(1.26 cm×1.26 cm)1个网格，轴向网格大小为5.355 cm。参考解为采用输运动力学程序NECP-X[13]进行同样pin-by-pin计算得到的结果。

归一化功率随时间的变化如图7所示，可看出：SP3近似的结果与参考解存在一定偏差，最大偏差在1.0 s时刻，归一化功率分别为0.138与0.124，主要是因为归一化功率绝对值非常低导致相对偏差较大。另外，参考解采用高阶输运MOC方法与SP3近似之间存在误差，在实际计算时SP3近似方法需结合合适的栅元均匀化技术。取第0.25、0.75、1.875、2.0和3.0 s时刻的径向二维功率分布和轴向一维功率分布，以NECP-X的功率分布结果为参考解，得到SP3近似的径向棒功率均方根相对偏差和最大相对偏差以及轴向一维功率分布的最大相对偏差和均方根相对偏差，结果列于表4。可看出：径向最大相对偏差和均方根相对偏差均出现在0.75 s，分别为-2.598%与1.006 4%；轴向最大相对偏差和均方根相对偏差均出现在第0.75 s，分别为0.389 9%和0.121 6%。其中，第0.75 s的径向棒功率相对偏差分布如图8所示，可看出相对偏差呈对角布置，MOX组件多为负偏差，UOX组件多为正偏差，但最大相对偏差均不超过3%。取第0.75 s的轴向功率分布及其相对偏差列于表5，可看出相对偏差主要在靠近反射层的活性区位置，但均不超过0.5%。

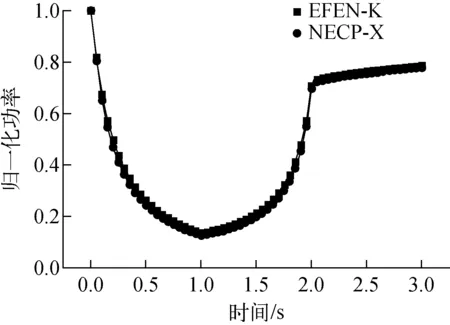
图7 三维多组件问题归一化功率随时间的变化Fig.7 Normalization power change with time of 3D multi-assembly problem

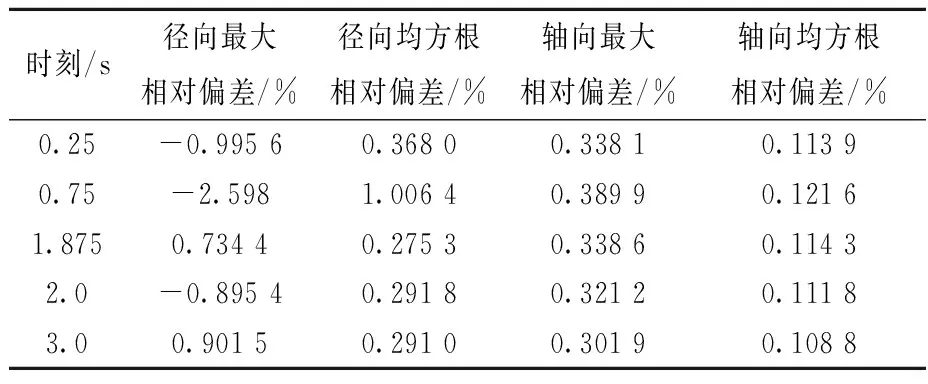
时刻/s径向最大相对偏差/%径向均方根相对偏差/%轴向最大相对偏差/%轴向均方根相对偏差/%0.25-0.995 60.368 00.338 10.113 90.75-2.5981.006 40.389 90.121 61.8750.734 40.275 30.338 60.114 32.0-0.895 40.291 80.321 20.111 83.00.901 50.291 00.301 90.108 8

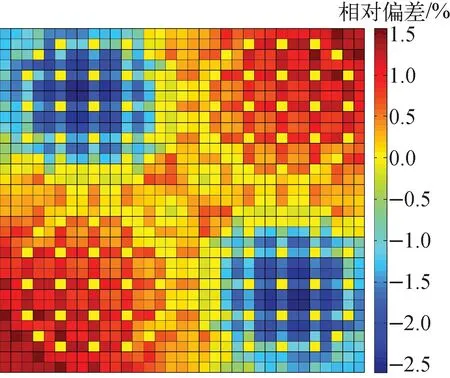
图8 三维多组件问题第0.75 s的SP3近似径向棒功率相对偏差分布Fig.8 Relative deviation distribution of radial rod power of SP3 calculation for 3D multi-assembly problem at 0.75 s

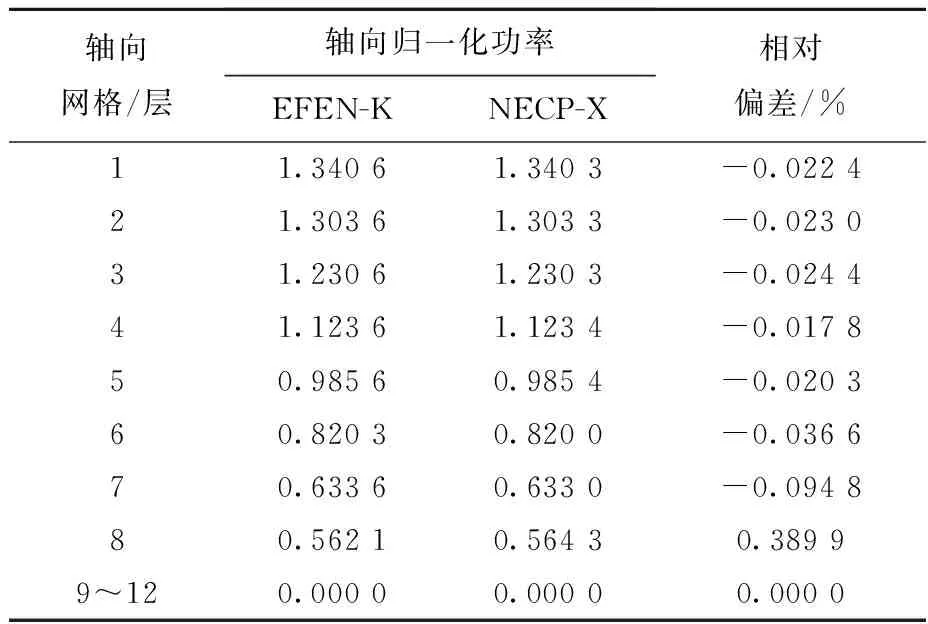
表5 三维多组件问题第0.75 s轴向棒功率分布及其相对偏差Table 5 Axial rod power distribution and relative deviation of 3D multi-assembly problem at 0.75 s

3 结论

为实现压水堆三维pin-by-pin中子动力学计算，本文研究了基于全隐式向后差分方法和EFEN-SP3方法的中子动力学计算技术，通过高阶源展开方法消除了固定源问题求解过程中的平源近似与缓发中子先驱核浓度计算中的高阶近似之间的不兼容问题，通过一系列加速方法有效提高了计算效率，并通过一系列算例的计算进行了数值验证与分析。数值结果表明：1) pin-by-pin中子动力学计算能直接给出安全分析所需的单棒功率密度分布，且计算结果与中子输运时空动力学程序NECP-X的pin-by-pin计算结果符合良好；2) 高阶源展开技术可有效抑制计算偏差随时间步的累加效应；3) 加速技术可将SP3动力学计算的求解速度提高134.9倍。