基于改进多区delta-tracking方法的蒙特卡罗中子输运跟踪与临界计算验证
2019-02-25陈珍平谢金森张震宇
陈珍平,谢金森,郭 倩,张震宇,谢 超,于 涛,*
(1.南华大学 核科学技术学院,湖南 衡阳 421001; 2.湖南省数字化反应堆工程技术研究中心,湖南 衡阳 421001; 3.南华大学 环境与安全工程学院,湖南 衡阳 421001)
蒙特卡罗方法因其计算精度高、几何适应性强、收敛速度与问题维数无关、具有优良并行计算特性等优势而被广泛应用于粒子输运问题的求解。因此,蒙特卡罗中子输运方法被国际反应堆物理界认为是新一代高精度堆芯物理分析方法的重要候选方法之一,也是近年来国际上的研究热点[1-2]。目前,相对于确定论方法而言,蒙特卡罗中子输运方法的最大缺点在于计算效率较低,这也是阻碍蒙特卡罗中子输运方法进行反应堆工程化应用的主要瓶颈之一。据相关研究表明[3-4],蒙特卡罗中子输运计算中约30%~80%的计算时间用于中子输运跟踪。因此,如何提高中子输运跟踪的效率是提高蒙特卡罗中子输运计算效率的重要手段。为弥补传统中子输运跟踪方法带来的潜在效率降低的缺陷,本文采用改进多区delta-tracking方法引入虚截面来对模型进行多区虚拟均匀化处理,进而在中子输运跟踪时则不考虑不同材料边界穿越问题,理论上可提高中子输运跟踪效率。
1 蒙特卡罗中子输运方法
蒙特卡罗中子输运方法的本质[5]就是模拟每个中子在给定模型系统中的随机游动历史,即模拟中子从产生到消失的运动过程。1个中子在介质系统中的游动历史可用1组状态参数来描述,中子的状态参数主要包括空间位置r、能量E和运动方向Ω,用状态变量S=(r,E,Ω)表示。假设1个源中子初始状态为S0=(r0,E0,Ω0),中子在介质材料中第m次碰撞后状态为Sm=(rm,Em,Ωm),其中rm为中子在第m次碰撞点的空间位置,Em为粒子在第m次碰撞后的能量,Ωm为粒子在第m次碰撞后的运动方向。因此,1个源中子在介质系统中随机游动,经过与介质靶核的若干次碰撞后,其游动历史结束(如被吸收或逃出系统)。因此,1个中子在系统中的游动历史可用1个状态序列表示为:S0,S1,S2,…,SM-1,SM。因此,蒙特卡罗方法的本质就是根据任意的中子状态Sm确定其碰撞后的下一个状态Sm+1,进而确定每个中子的状态序列(即游动历史)。如图1所示,当中子在系统中随机游动时,由状态Sm=(rm,Em,Ωm)(m=1,2,…,M-1)经过碰撞达到状态Sm+1=(rm+1,Em+1,Ωm+1)时,需通过中子输运跟踪确定其第m+1个状态的空间位置rm+1、能量Em+1和运动方向Ωm+1。其中,中子输运跟踪的1个重要任务就是确定中子从Sm状态到达Sm+1状态时的飞行距离。
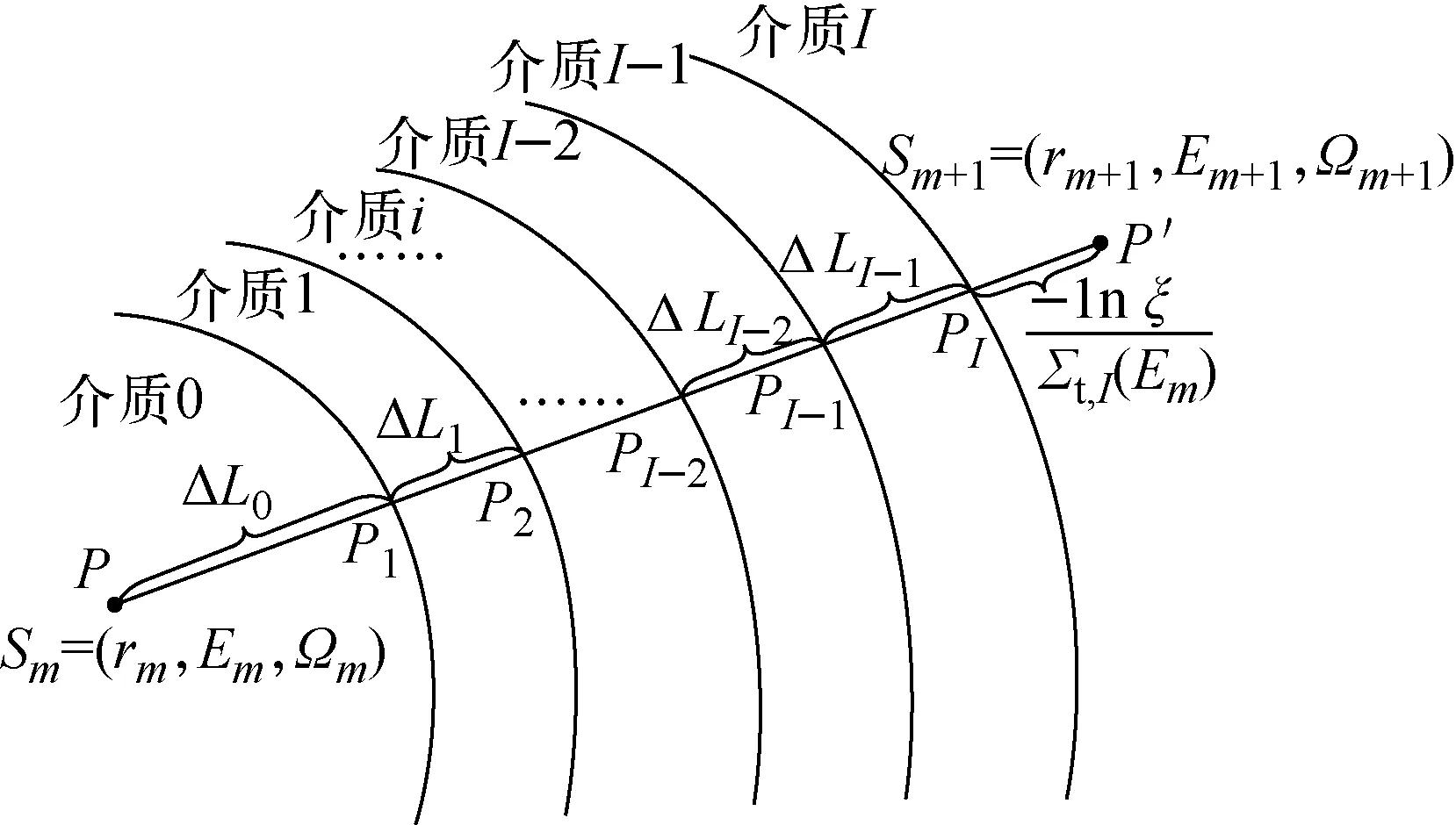
图1 传统中子输运跟踪方法Fig.1 Traditional neutron transport tracking method
假设中子以Sm状态出发,以Em能量、沿Ωm方向飞行L长度后,发生第m+1次碰撞时的位置为rm+1=rm+LΩm,其中L称为中子两次碰撞之间的输运长度。由核反应堆物理理论可知,输运长度L服从的概率密度分布函数为:
f(L)=Σt(rm,Em)·
(1)
其中:Σt为介质材料的宏观总截面;l为中子的飞行径迹长度。对于式(1),当中子在均匀介质中输运时,则输运长度抽样为:
(2)
其中,ξ是在0~1区间内均匀分布的随机数。但是,当中子在非均匀介质系统中进行输运时(图1),可能会依次穿过多层介质才发生碰撞,根据指数分布的无记忆特点,此时需逐层考虑中子是否在该层介质发生碰撞;如果不发生碰撞,则中子将沿当前方向继续飞行到下一层介质边界处,再判断是否在该层介质发生碰撞,直到中子在某一第I层介质发生碰撞,此时输运长度抽样为:
(3)
其中:ΔLi为中子由rm出发、沿Ωm方向随机游动、在第i个介质区域内飞行的距离;Σt,I(Em)为中子发生碰撞反应的第I层介质的宏观总截面。如图1所示,在进行非均匀介质系统(如实际燃料组件或反应堆堆芯)蒙特卡罗中子输运计算时,为确定式(3)的中子输运长度,传统中子输运跟踪方法需根据中子射线方程与几何模型的边界面方程,联立求解计算ΔLi。因此,在蒙特卡罗中子输运计算中,为确定式(3)的输运长度,当中子的平均自由程大于局部模型的宏观尺寸时,频繁大量的ΔLi距离计算是导致中子输运跟踪效率降低的主要原因之一。
2 传统单区delta-tracking中子输运跟踪方法
为弥补在传统中子输运跟踪方法中,中子每次穿越材料边界时都需要频繁地进行距离计算带来效率降低的缺陷,Woodcock等[6]提出了delta-tracking方法来解决这一问题,其基本原理是假设1个模型共包含N个几何体,每个几何体均被赋予了一种特定材料,整个模型中共有M种材料。传统delta-tracking方法通过给每种材料的宏观总截面添加1个虚截面,然后整个模型被虚拟均匀化为单一均匀介质材料来进行蒙特卡罗中子输运跟踪(单区delta-tracking方法),从而中子每步的输运长度便可根据式(2)直接获得,即使中子穿越材料边界时,也不再需进行边界距离计算,从而节省了中子输运跟踪时间,提高了中子输运计算效率。
图2示出基于传统单区delta-tracking的中子输运跟踪方法。假设1个模型中包含M种介质材料M1,M2,M3,…,MM,对于中子处于某一能量Ei,各材料在该能量Ei下的宏观总截面为Σt,1,Σt,2,Σt,3,…,Σt,M。对所有材料对应能量下的宏观总截面进行如下处理:
Σt,max=max{Σt,1,Σt,2,Σt,3,…,Σt,M}
(4)
Σt,max=Σt,1+Σ1,δ=
Σt,2+Σ2,δ=…=Σt,M+ΣM,δ
(5)
其中:Σt,max为当前Ei能量下所有M种材料中宏观总截面的最大值;Σ1,δ,Σ2,δ,Σ3,δ,…,ΣM,δ为虚截面,这些截面数据是人为定义和添加的。此时,整个模型被当成一种均匀介质来处理,可用式(2)直接进行输运长度抽样,进而避免了多次边界距离计算,提高了中子输运跟踪效率。
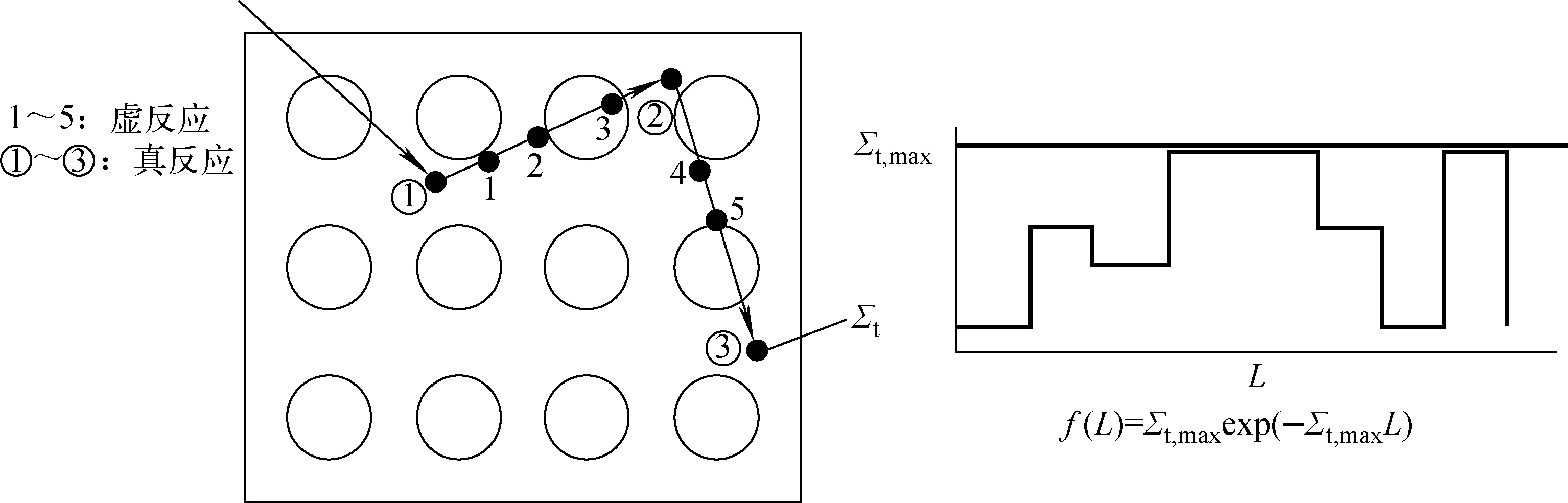
图2 传统单区delta-tracking中子输运跟踪方法Fig.2 Neutron transport tracking based on traditional single-regional delta-tracking method
此时根据式(2),中子每步的输运长度抽样为:
(6)
由于给每种材料的宏观总截面引入了虚截面,因此式(6)中抽样采用的Σt,max是包含虚截面部分的。因此为排除因虚截面的引入而带来的与真实中子输运物理问题的偏差,需将中子物理反应分为真反应和虚反应(或假反应),也就是按照式(6)进行输运长度抽样并进行中子输运跟踪时,需采用拒绝抽样来判断真假中子物理反应,其判断条件如下。
1) 当中子按式(6)输运长度随机游动1步后,到达第i种介质材料,然后判断是否满足条件:ξ1<Σt,i/Σt,max(Σt,i为中子当前碰撞点处材料的宏观总截面,ξ1为抽样在0~1之间的随机数);如果满足该条件,则中子在该点发生真实物理反应(真反应),从而进行后续的反应核素、反应类型、中子反应后状态进行抽样,然后进行下一步输运。
2) 反之,如果不满足上述判断条件,则中子在该点发生虚反应或假反应,此时中子的能量和运动方向不发生变化,继续以式(6)抽样新的输运长度(此时需抽样新的随机数),并以原来的能量沿原来运动方向向前飞行;然后返回步骤1重新进行判断,直到中子发生真实物理反应、被吸收或离开系统为止。
3 改进多区delta-tracking中子输运跟踪方法
3.1 基本原理
在传统单区delta-tracking中子输运跟踪方法中,对一个含有M种材料的模型,通过引入唯一一个当前中子能量下的最大宏观总截面Σt,max来对整个模型进行单区虚拟均匀化处理,将非均匀介质转化为单一均匀介质,此时将输运长度抽样公式由式(3)简化为式(6)以提高中子输运跟踪效率。然而研究发现,当模型局部区域存在强中子吸收体(或Σt,max较大的材料)时,此时模型部分材料区域(除强中子吸收体外的区域)满足Σt,i≤Σt,max,则有Σt,i/Σt,max≈0,这时中子输运跟踪过程进行拒绝抽样时会出现大量虚反应,这一现象反而会导致delta-tracking跟踪效率降低[7-8]。为弥补这一缺陷,本文提出了基于改进多区delta-tracking的中子输运跟踪方法。
通过对传统单区delta-tracking方法分析,导致其效率降低的潜在因素在于,由于强中子吸收体(宏观总截面较大的材料)的存在,导致强中子吸收体的Σt,max与其他材料的Σt,i相比量级大太多。为解决该问题,采用改进多区delta-tracking方法,根据模型中各区域材料对中子的吸收特性,对整个模型进行区域分解,将模型划分为多个虚拟均匀化区域(子区域),在每个虚拟均匀化子区域内再采用单区delta-tracking方法跟踪。在进行区域划分时,直接利用构成模型的几何曲面进行划分,例如以燃料组件的边界面(图3)进行虚拟划分可得到多个子区域。此时,中子在不同子区域进行delta-tracking跟踪时,进行输运长度抽样及拒绝抽样时采用的Σt,max仅是当前虚拟均匀化子区域内包含材料的最大宏观总截面,而每个子区域delta-tracking跟踪时采用的Σt,max互不相同且互不影响。
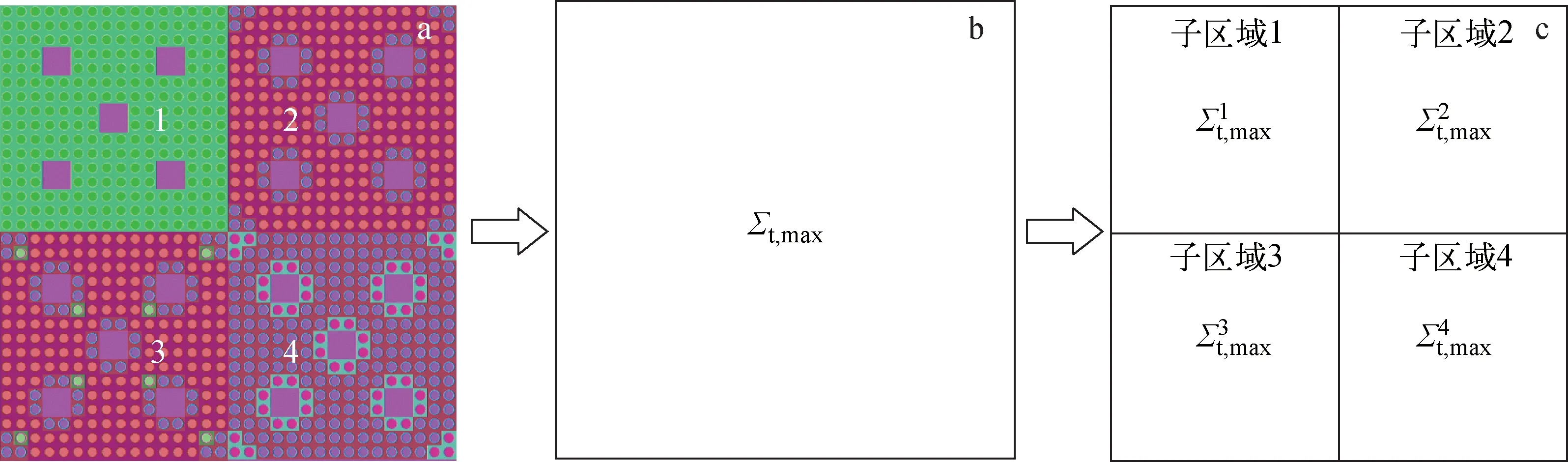
a——组件模型;b——单区delta-tracking跟踪;c——多区delta-tracking跟踪图3 改进多区delta-tracking中子输运跟踪方法Fig.3 Neutron transport tracking based on improved multi-regional delta-tracking method
以图3a所示模型为例,其包含4个燃料组件,假设整个模型包含M种材料,其中1、2、3、4号组件各包含M1、M2、M3、M4种材料。在进行delta-tracking中子输运跟踪时,利用式(6)进行输运长度抽样及拒绝抽样时,对传统单区delta-tracking跟踪(图3b),其最大宏观总截面为:
(7)
对于改进多区delta-tracking跟踪(图3c),假设将整个模型以组件为单位划分为4个虚拟均匀化子区域进行中子输运跟踪,跟踪时各子区域的最大宏观总截面为:
(8)
通过分析式(7)、(8)可知,将单区改进为多区跟踪时,可减小Σt,max与Σt,i之间的量级差异。因此,通过将传统delta-tracking方法的单区全局跟踪方式改进为基于多区的局部跟踪方式,可有效避免因某个或几个子区域存在强中子吸收体而导致其他区域中子输运跟踪效率降低的现象。
3.2 无偏性证明
在进行delta-tracking中子输运跟踪时,当中子穿越材料边界时不再进行式(3)的边界距离计算,而此时的跟踪过程与传统蒙特卡罗中子输运跟踪方法完全不同。但从概率论和统计学上来讲,中子经delta-tracking输运跟踪得到的最终统计结果与采用传统中子输运跟踪方法所得到的结果是一致的,即delta-tracking方法对中子输运计算结果的统计是无偏的。以下证明给出了delta-tracking方法对输运结果统计的无偏性。
假设1个给定能量的中子在介质中穿过路程L仍未发生反应的概率为P(L)。由式(5)可知Σt,max=Σt+Σδ,则对该式两边从0到L进行积分有:

(9)
在中子输运1步时,中子可能经过0次,1次,2次,…,n次虚反应到达L处,则有:

(10)
其中,P(L|n)可由如下得到:
P(L|0)=e-Σt,maxL
(11)


(12)
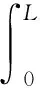
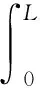
(13)

(14)
因此,中子穿过L长的路程仍未发生核反应的概率P(L)为:
(15)
由式(15)可知,在delta-tracking跟踪方法中,中子输运长度仍服从负指数分布,与传统的蒙特卡罗中子输运跟踪过程中,中子输运长度服从的概率密度分布函数(式(1))在本质上是一致的。因此,delta-tracking跟踪方法对中子输运结果统计是无偏的。
3.3 中子输运跟踪流程
基于改进多区delta-tracking方法的中子输运跟踪流程如图4所示,给出了中子完成1步随机游动过程的输运跟踪流程。
4 数值验证
本文将改进多区delta-tracking中子输运跟踪方法在NEAL团队开发的多功能辐射输运模拟仿真平台MOSRT系统[9]中进行了程序实现。本文开展数值验证时分为两个层面:为验证本文方法及程序的正确性与有效性,从国际临界安全基准评价实验手册中选择40道基准题模型(多层介质几何模型)开展临界计算验证;为进一步验证本文方法及程序对于复杂问题的适应性,选取3个全堆芯模型开展临界计算验证,以证明本文方法及程序对于复杂问题同样有效。其中,本文在Windows 7系统下采用单核Intel Core i5-5200 2.20 GHz处理器开展数值验证,临界计算条件为:共计算3 000个循环代,跳过500个非活跃代,每代5 000个中子,以计算得到的有效增殖因数(keff)作为正确性验证,以完成临界计算的计算时间作为效率提升的有效性验证。

图4 基于改进多区delta-tracking的中子输运跟踪流程Fig.4 Neutron transport tracking procedure based on improved multi-regional delta-tracking method
4.1 基准题模型临界验证
为减小计算结果的统计涨落,保证计算的准确性,蒙特卡罗临界计算keff时通常采用径迹长度估计、碰撞估计和吸收估计3种方法进行组合计算[10]。然而,基于delta-tracking方法进行中子输运跟踪时,无法统计中子在每个材料区域单独的径迹长度,导致计算keff时无法采用径迹长度估计进行组合计算。因此,根据keff的物理定义,本文采用直接估计法[11](新生一代的裂变中子数目与其直属上一代的中子数目之比)代替径迹长度估计法,以保证keff计算的准确性。
国际临界安全基准评价实验手册(ICSBEP)[12]是由OECD-NEA组织编撰,用于校验临界计算方法和程序正确性的实验基准题库。为验证本文方法及程序实现的正确性,从手册中选取了40道基准题,其主要为多层平板、球壳、圆柱及铀水棒栅等临界实验装置,且覆盖不同燃料富集度、燃料类型和中子能谱。其中,根据235U的富集度分成高富集度、中富集度和低富集度铀;燃料类型包括金属燃料和溶液燃料;中子能谱包括快谱和热谱。因此,40道基准题根据铀富集度、燃料类型及中子能谱分为4类:1) hmf系列,高富集度、金属燃料、快谱基准题;2) hst系列,高富集度、溶液燃料、热谱基准题;3) imf系列,中富集度、金属燃料、快谱基准题;4) lst系列,低富集度、溶液燃料、热谱基准题。
表1列出基于多区delta-tracking(MDT)方法、单区delta-tracking(SDT)方法和传统中子输运跟踪方法(TTM)对40道基准题进行蒙特卡罗临界计算得到的keff结果,并以MCNP程序计算结果作为基准校验,同时给出实验值作为参考。从表1可知,基于MDT和SDT方法得到的keff计算结果与TTM结果的最大偏差分别为45 pcm和121 pcm,说明MDT、SDT方法与TTM符合较好;同时,以MCNP结果作为基准校验,MDT、SDT和TTM 3种方法得到的keff结果与MCNP结果的最大偏差分别为53、69和64 pcm,且3种方法的计算结果均落在MCNP结果的标准差内,说明在相同的临界计算条件下3种方法与MCNP程序符合一致。因此,通过临界基准题的计算分析以及与MCNP程序的基准校验,证明了本文方法及程序的正确性。
表2列出基于SDT和MDT方法进行蒙特卡罗临界计算时得到的加速比。从表2可知,基于delta-tracking方法可有效提升蒙特卡罗临界计算的效率,可得到最大加速比为1.8。同时,通过临界基准题的计算验证发现,MDT方法得到的加速比略大于SDT方法,说明MDT方法的中子输运跟踪效率优于SDT方法,证明了本文方法及程序在蒙特卡罗临界计算效率提升方面的有效性。
4.2 全堆芯模型临界验证
为进一步验证本文方法及程序在复杂问题计算中的适应性,采用全堆芯模型对其进行正确性和有效性验证,本文采用OPR、HM和BEAVRS 3个不同复杂度的全堆芯压水堆(PWR)模型开展了蒙特卡罗临界计算验证。其中,OPR模型[13]由177个5种不同富集度燃料组件组成,每个燃料组件为16×16的棒栅布置;HM模型[14]由241个相同的燃料组件组成,每个燃料组件为17×17的棒栅布置;BEAVRS模型[15]由193个多种类型的燃料组件组成,每个燃料组件为17×17的棒栅布置。具体堆芯布置和结构组成如图5所示。
针对3个全堆芯模型进行了临界计算keff正确性验证。表3列出采用3种中子输运跟踪方法得到的keff结果,并以MCNP程序计算结果作为基准校验。从表3可知,基于MDT和SDT方法得到的keff结果与TTM结果的最大偏差分别为15 pcm和47 pcm,说明MDT、SDT方法与TTM符合较好。同时以MCNP结果作为基准校验,MDT、SDT和TTM 3种方法得到的keff结果与MCNP结果的最大偏差分别为18、46和33 pcm,且3种方法的计算结果均落在MCNP结果的标准差内,说明3种方法与MCNP程序符合一致。因此,数值结果证明了本文方法及程序在复杂全堆芯模型实际应用中的正确性。
表4列出对3个全堆芯模型进行临界计算keff的有效性验证,以证明本文方法在处理复杂全堆芯模型时在中子输运跟踪效率提升方面的有效性。从表4可知,MDT方法的中子输运跟踪效率明显优于TTM和SDT方法,其对3个模型临界计算的平均加速比约为1.4、1.5和1.6。因此,数值结果证明了本文方法及程序在复杂全堆芯模型实际应用中的有效性。
5 结论
针对传统蒙特卡罗中子输运跟踪方法存在的效率降低问题,本文提出了改进多区delta-tracking中子输运跟踪方法以提高中子输运跟踪效率。本文对改进多区delta-tracking方法的原理及跟踪流程进行了详细阐述,并利用国际临界安全实验基准题和典型全堆芯压水堆模型开展了蒙特卡罗临界计算验证。数值结果表明,改进多区delta-tracking方法的临界计算结果与传统中子输运跟踪方法的计算结果符合一致,且中子输运跟踪效率得到明显提升,证明了本文方法及程序的正确性和有效性。
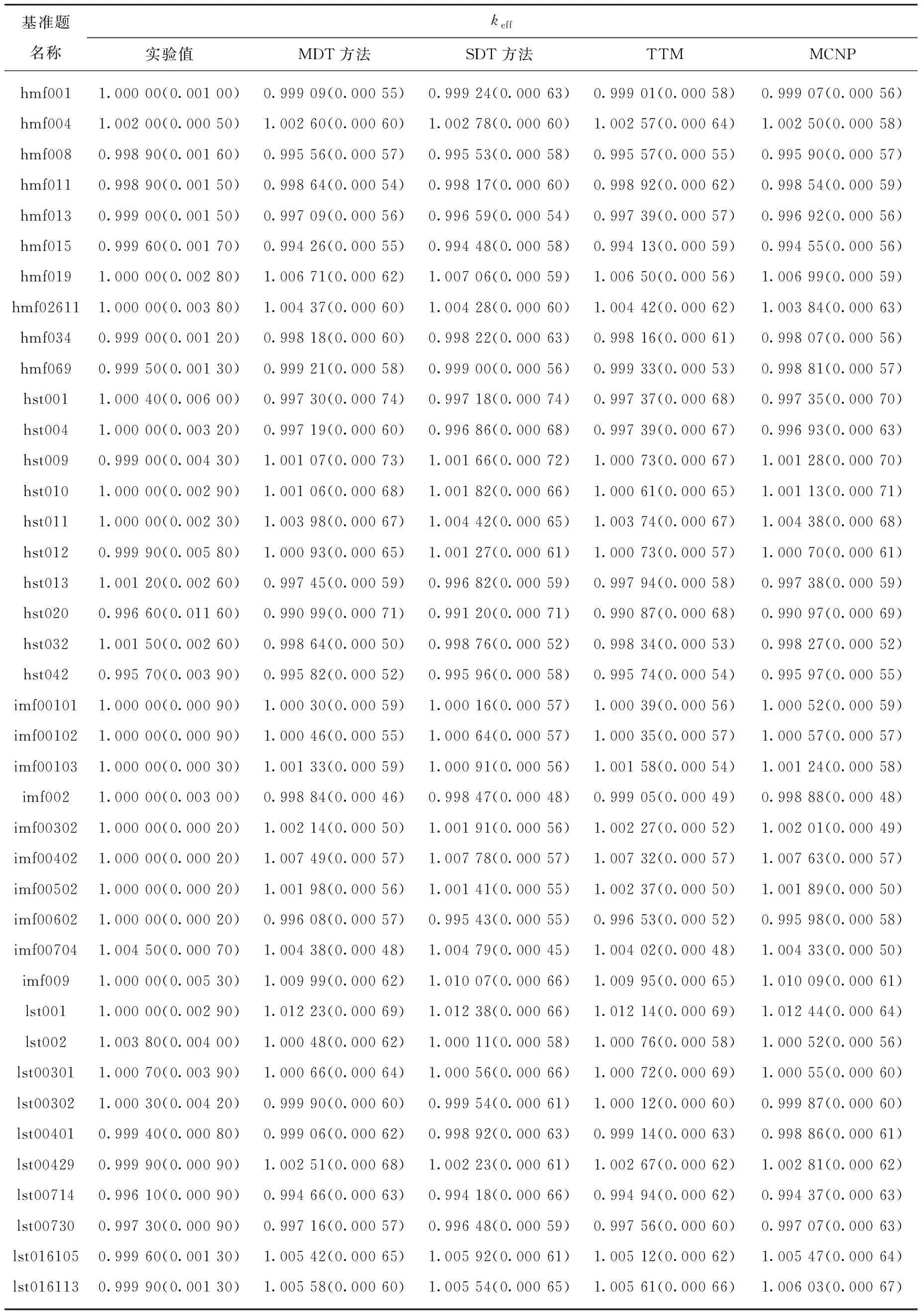
表1 国际临界安全基准题模型临界计算正确性验证Table 1 Verification of accuracy for ICSBEP benchmark criticality calculation
注:括号内数据为标准差
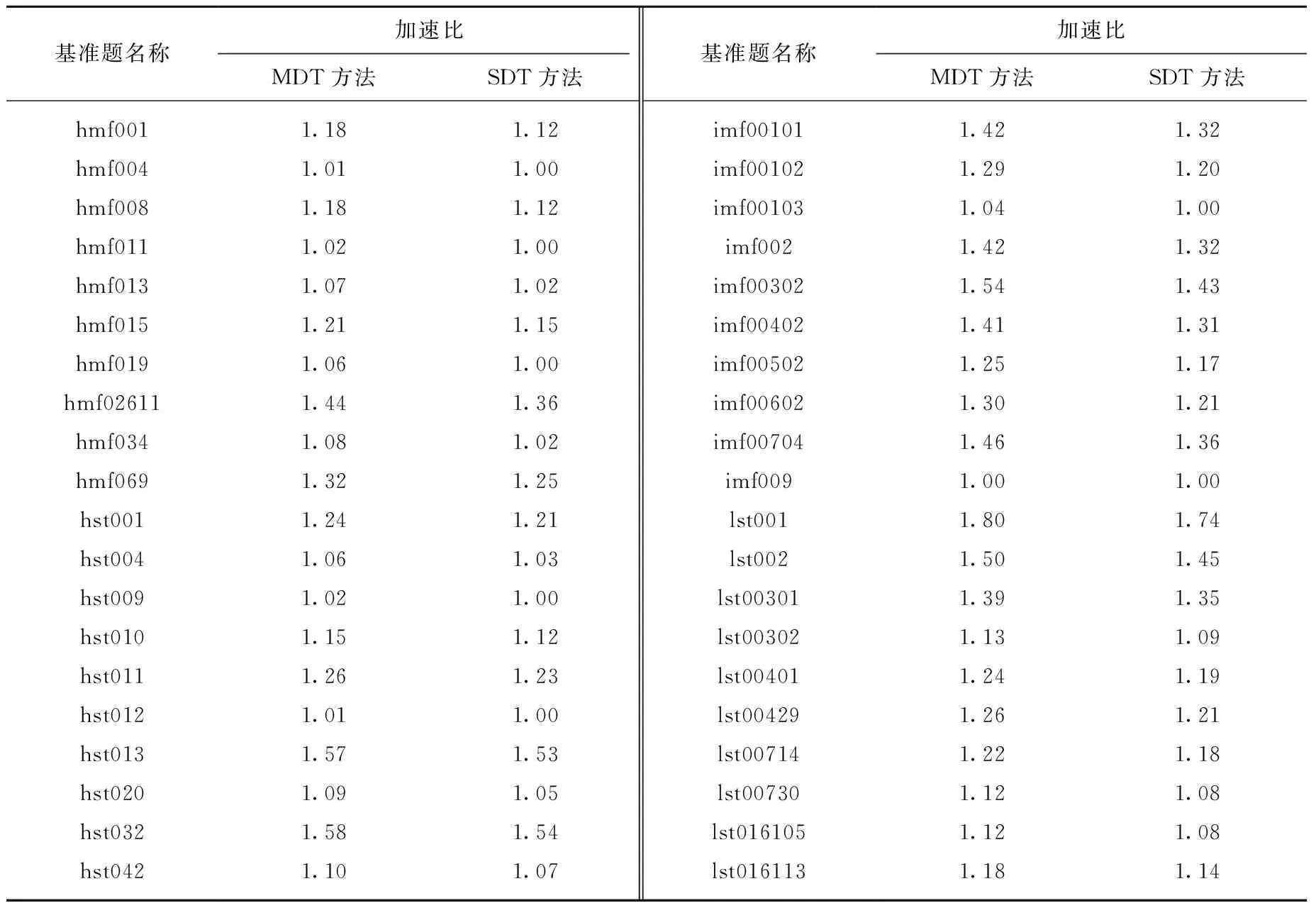
表2 国际临界安全基准题模型临界计算有效性验证Table 2 Verification of efficiency for ICSBEP benchmark criticality calculation
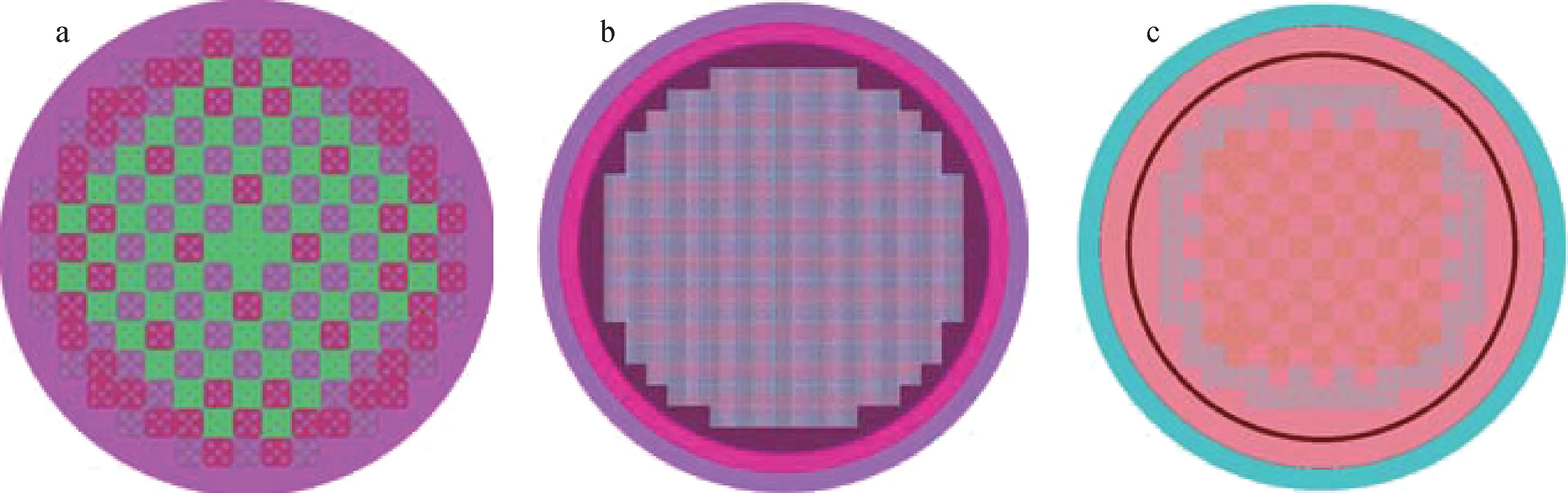
a——OPR模型;b——HM模型;c——BEAVRS模型图5 全堆芯压水堆模型Fig.5 Whole-core PWR model

全堆芯模型keffMDT方法SDT方法TTMMCNPOPRHMBEAVRS1.006 10(0.000 85)1.001 28(0.000 59)1.005 05(0.000 72)1.005 95(0.001 05)1.001 58(0.000 68)1.005 37(0.000 84)1.006 23(0.000 91)1.001 16(0.000 57)1.004 90(0.000 72)1.006 24(0.000 82)1.001 12(0.000 64)1.005 23(0.000 68)
注:括号内数据为标准差
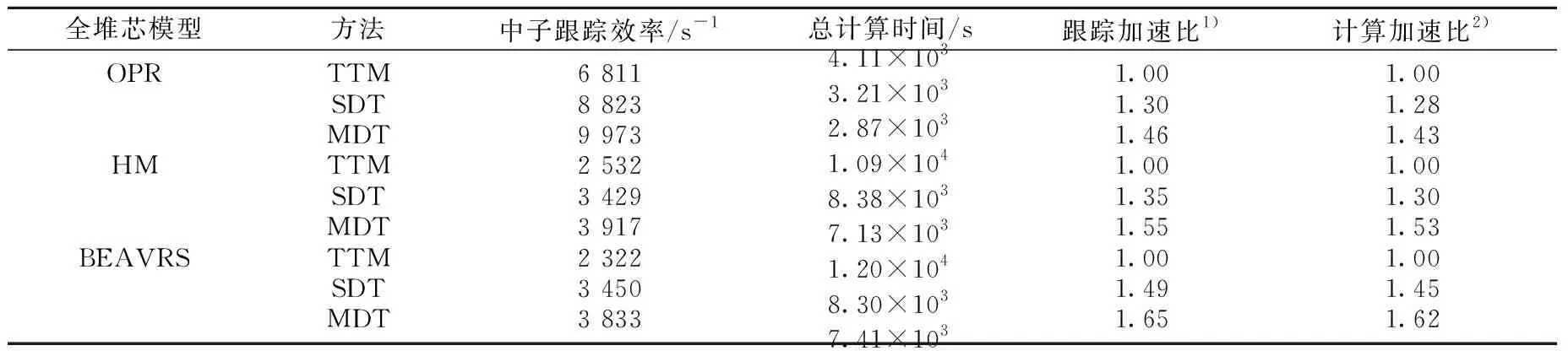
表4 全堆芯压水堆模型临界计算有效性验证Table 4 Verification of efficiency for whole-core PWR criticality calculation
注:1) 当前中子输运跟踪方法与传统中子输运跟踪方法的中子跟踪效率之比
2) 传统中子输运跟踪方法与当前中子输运跟踪方法的总计算时间之比
