低复杂度的正交空间调制检测算法
2019-02-25唐青青李兆玉李若梦
唐青青,李兆玉,李若梦
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
0 引 言
与单输入单输出(single-input single-output,SISO)相比,传统的多输入多输出(multiple-input multiple-output,MIMO)技术使用多根发送天线来发送多个数据流[1],在保证系统可靠传输的前提下能够大幅度地提高数据传输速率。然而,MIMO方案也存在一些弊端:需要较高的天线同步(inter-antenna synchronization,IAS)来满足同时传输数据的要求;接收端将产生较高的信道间干扰(inter-channel interference,ICI),增加了译码和计算的难度;多天线同时工作需要多个射频链路(radio frequency,RF),增加了系统成本和开销[2]。为了解决上述问题,空间调制(spatial modulation,SM)技术被提出。
作为一种新型的多输入多输出技术,空间调制以一种新的方式来使用多根发送天线,能够在不增加信道带宽和发射功率的前提下有效地提高系统容量和频谱效率[3]。与传统的多输入多输出方法不同,空间调制[4-5]技术除了传统的符号映射承载了部分信息以外,天线序号也携带了部分比特信息,即一部分比特用来选择激活天线的序号,另一部分比特用来进行传统的符号调制。用来选择激活天线序号的那部分比特并不通过信道直接进行传输,而是隐含在激活天线序号中,接收端只需要进行相应的检测与解调,这部分比特信息便可恢复。在一个时隙里单根天线被激活,这样就完全避免了IAS和ICI问题。虽然,空间调制是一种非常有效的提高传统多输入多输出方案频谱效率的方法,但是频谱效率较低。为了提高系统吞吐量,一种新的方案被提出来,新方案被命名为正交空间调制系统(quadrature spatial modulation,QSM),并且正交空间调制技术几乎保留了传统空间调制所有的优点。
正交空间调制[6],是一种在发送端对发送信号进行预处理的调制技术,在发端它把空间星座符号分解成正交分量和同向分量2部分,然后这2部分分别搭载到正弦和余弦载波上由2根被激活的天线发射出去。而值得注意的是,在空间调制系统中,单根天线被激活来发送这2部分信息,所以在频谱效率上,与传统的空间调制系统相比,正交空间调制系统能够提高lbNt个比特[7],Nt表示发端发送天线的个数。
空间调制由于单天线激活从而能够消除信道间干扰。在正交空间调制系统中,因为2种载波相互正交,同样信道间干扰也能消除。正交空间调制检测,不仅要在接收端检测出发送符号实部和虚部的激活天线,还要根据激活天线对应的实部和虚部来得到发送的星座符号,最终才能恢复出发送比特流。传统的空间调制只需检测单根发送天线和对应的星座点符号,而这无疑在接收端增加了检测的难度和复杂度。目前,空间调制的检测算法研究已相当成熟,而正交空间调制检测算法的研究还很少,有进一步研究的空间,而传统的检测算法在性能和复杂度上只能表现出一个优势,这就需要一种既能确保较性能较优又能使复杂度增加较小的检测算法。
本论文将传统线性检测方案—迫零(zero forcing,ZF)、最小均方误差(minimum mean square error,MMSE)应用于正交空间调制系统中[8-11]。仿真结果表明,虽然线性检测算法复杂度较低,但是误比特性能却很差[12]。为了更好地实现复杂度和性能之间的均衡,增强型迫零检测算法被提出。该算法将检测过程分为2个步骤:①天线检测;②符号检测。在步骤1中,检测出可能的发送天线组合(transmit antenna combinations,TACs);在步骤2中,基于步骤1检测出的可能的发送天线组合,采用最大似然思想检测出具体的调制符号。在增强型迫零和最大似然2种检测算法的结合下,实现了复杂度和性能之间的折中考虑。
1 系统模型
1.1 信道模型
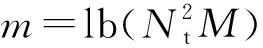
(1)
然而,在空间调制技术中,每个时隙只激活一根天线用来发送xR和xI。因此,与空间调制相比,正交空间调制中每个时隙传输的比特数增加了lbNt。因为正弦和余弦载波相互正交,所以在正交空间调制系统中信道间干扰不必考虑。因为每个时隙激活的天线个数最多是2,所以天线间同步的要求也降低了。在正交空间调制技术中,可以使用空间分离器将一个信号的实部和虚部分别分配给相应的激活天线[6]。
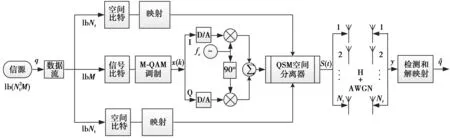
图1 正交空间调制系统模型图Fig.1 QSM system model diagram
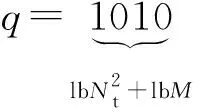
(2)
正交空间调制系统发送比特数为4 bit时的具体映射如表1所示。
1.2 最大似然-最优检测
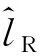
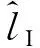
(3)
由于最大似然检测算法需要穷尽搜索所有的激活天线和所有的信号调制星座点,因此,ML检测算法有着相当高的计算复杂度。
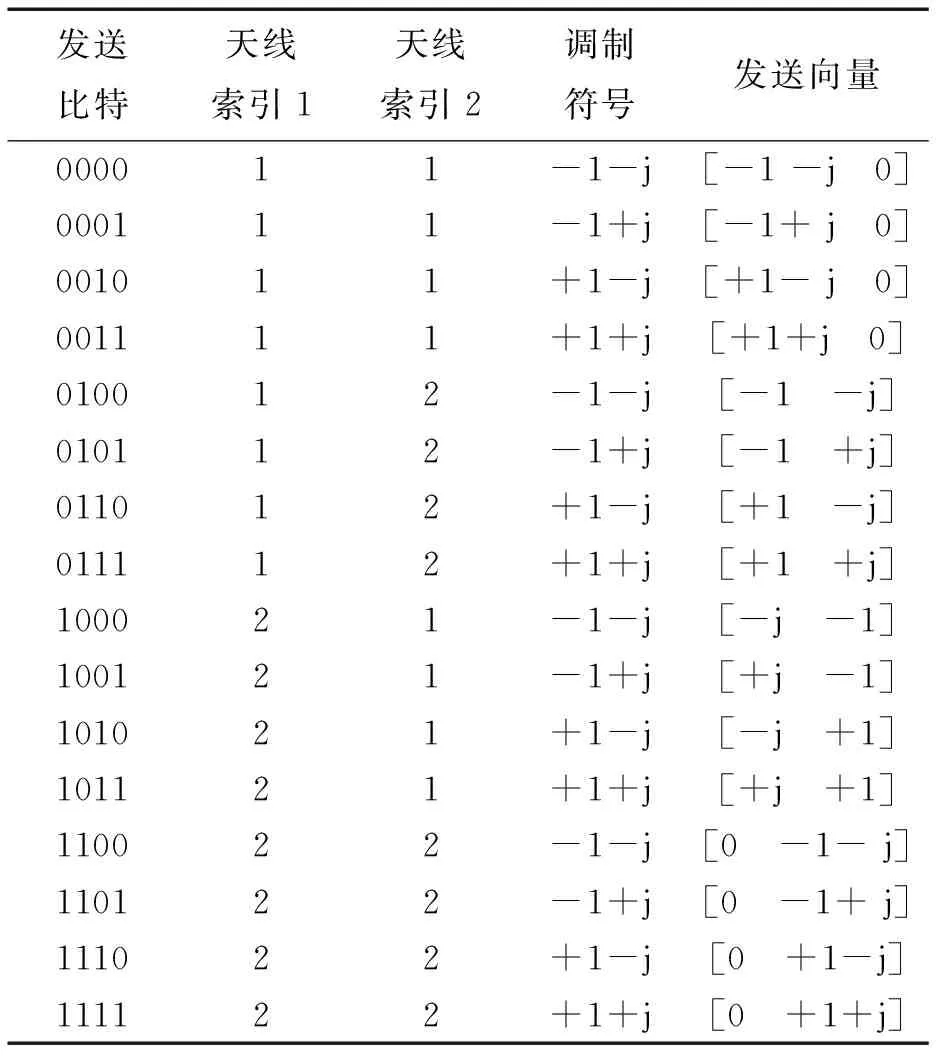
表1 正交空间调制映射表
1.3 迫零检测
迫零检测是一种低复杂度的线性检测方案,迫零检测[8]具体实现可表示为
(4)
(4)式中:H+表示信道矩阵H的伪逆;(·)H表示一个向量或矩阵的复共轭转置;(·)-1表示逆矩阵。
从(2)式和(4)式可以看出,ZF检测可以消除来自其他天线的干扰,且在高信噪比下(signal to noise ratio,SNR)能够获得较好的误比特性能。然而,ZF检测却放大了噪声,尤其在信道响应的零点。
1.4 最小均方误差检测
最小均方误差也是一种低复杂度的线性检测算法。由于最小均方误差将噪声考虑进去,所以它能够获得比迫零检测较好的误比特性能。最小均方误差[8]具体公式为
(5)
(5)式中,ρ表示每一根接收天线的平均信噪比。最小均方误差基于最大输出信干噪比的考虑,目的是在噪声抑制和干扰消除之间找出一个最优平衡点。因此,与迫零检测相比,最小均方误差是一个较好的选择。
2 提出的检测算法
本论文提出了一种基于迫零的正交空间调制系统检测方案。对于ZF,MMSE以及提出的EZF 3种检测算法,检测过程都是分为2步,即可能的发送天线组合检测和基于可能的发送天线组合利用ML思想的符号检测。与ML相比,ZF和MMSE都有着较差的性能。本论文的主要贡献是提出了一种低复杂度且性能较ZF和MMSE优的新方案。
2.1 增强型迫零检测
迫零是对信道矩阵H直接求伪逆的过程,是一种最简单的低复杂度检测算法。然而,在迫零检测中,要想获得较好的性能,接收端就需要更多的接收天线。因此,为了不增加硬件成本而又提高性能,一种新的低复杂度线性检测方案被提出,命名为增强型迫零检测算法。提出的检测算法有着比ZF和MMSE更低的误码率性能,具体实现如下。
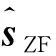
(6)
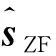
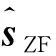
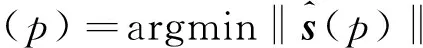
(7)
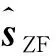
步骤3执行多次迫零以后,得到一个2维的发送天线索引
TA″=[i,j]T
(8)
(8)式中,i,j∈[1,…,Nt]。正交空间调制一个时隙激活发送天线数最多为2,当激活天线数为1时,表示符号实部和虚部在同一根天线发送。对上述得到的2维向量中的元素进行重组,可得到发送天线组合(transmit antenna combination,TAC),用RTA表示为
(9)
根据矩阵RTA中3 种可能的天线组合,星座符号x和相应的发送天线组合可通过ML思想被检测出来。发送天线索引和星座符号可由(10)式得到
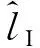
(10)
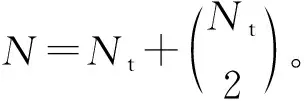
2.2 计算复杂度
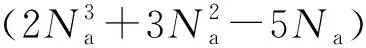
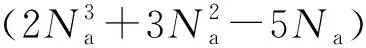

表2 正交空间调制系统中不同算法的复杂度
3 计算机仿真结果
在平坦瑞利衰落信道下,本节将考虑至少106次蒙特卡洛仿真结果来比较QSM和SM的性能。仿真结果也给出了提出的检测算法与迫零、最小均方误差以及最大似然间的性能和复杂度比较情况。
3.1 正交空间调制与空间调制的性能比较
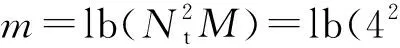
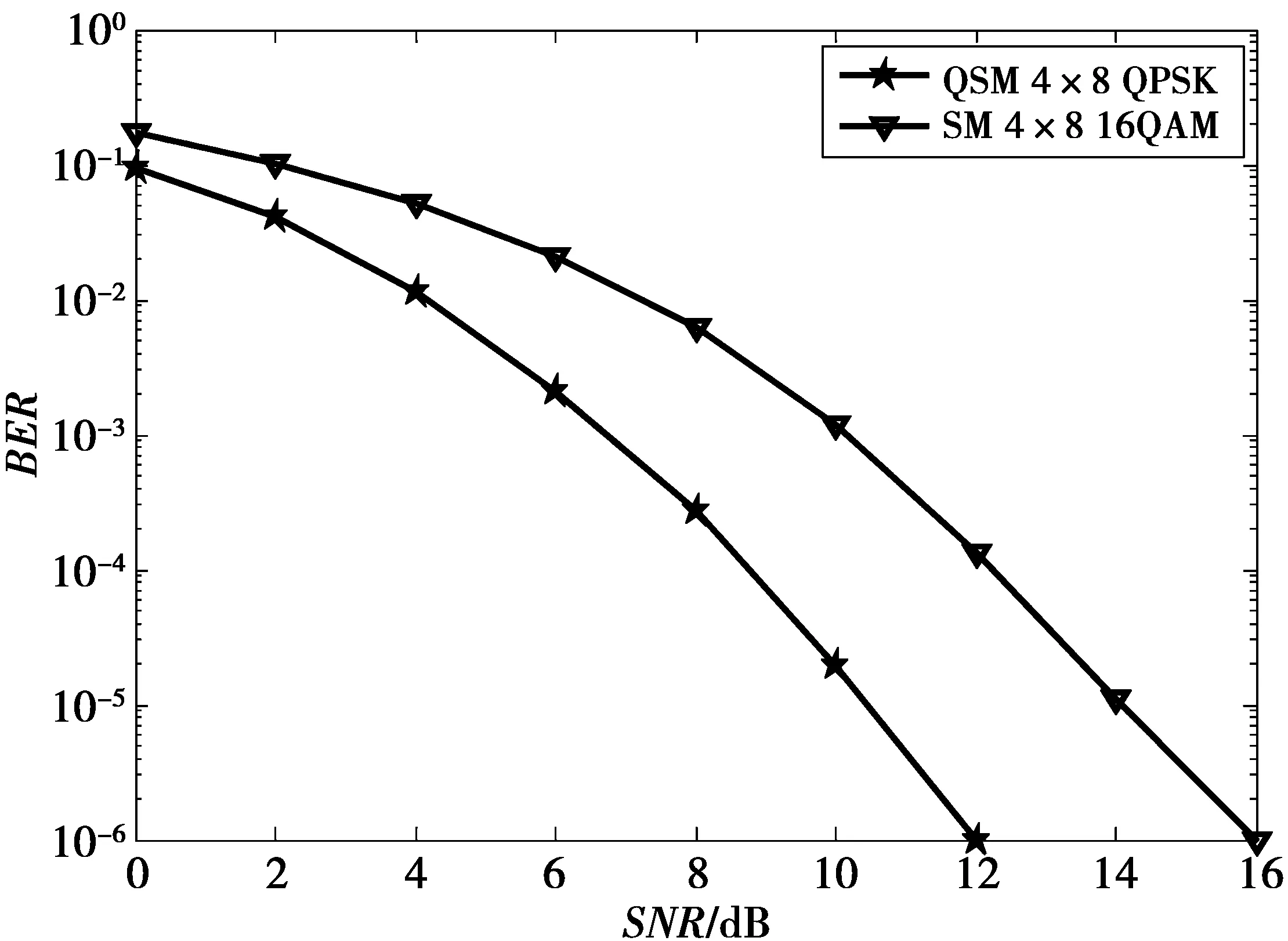
图2 正交空间调制与空间调制在最大似然检测下的性能比较Fig.2 BER performance comparison between QSM and SM under ML detection
3.2 正交空间调制系统的性能分析
为了比较不同频谱下ZF,MMSE,EZF之间的性能,本部分进行了一系列的仿真,结果如下。
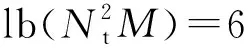
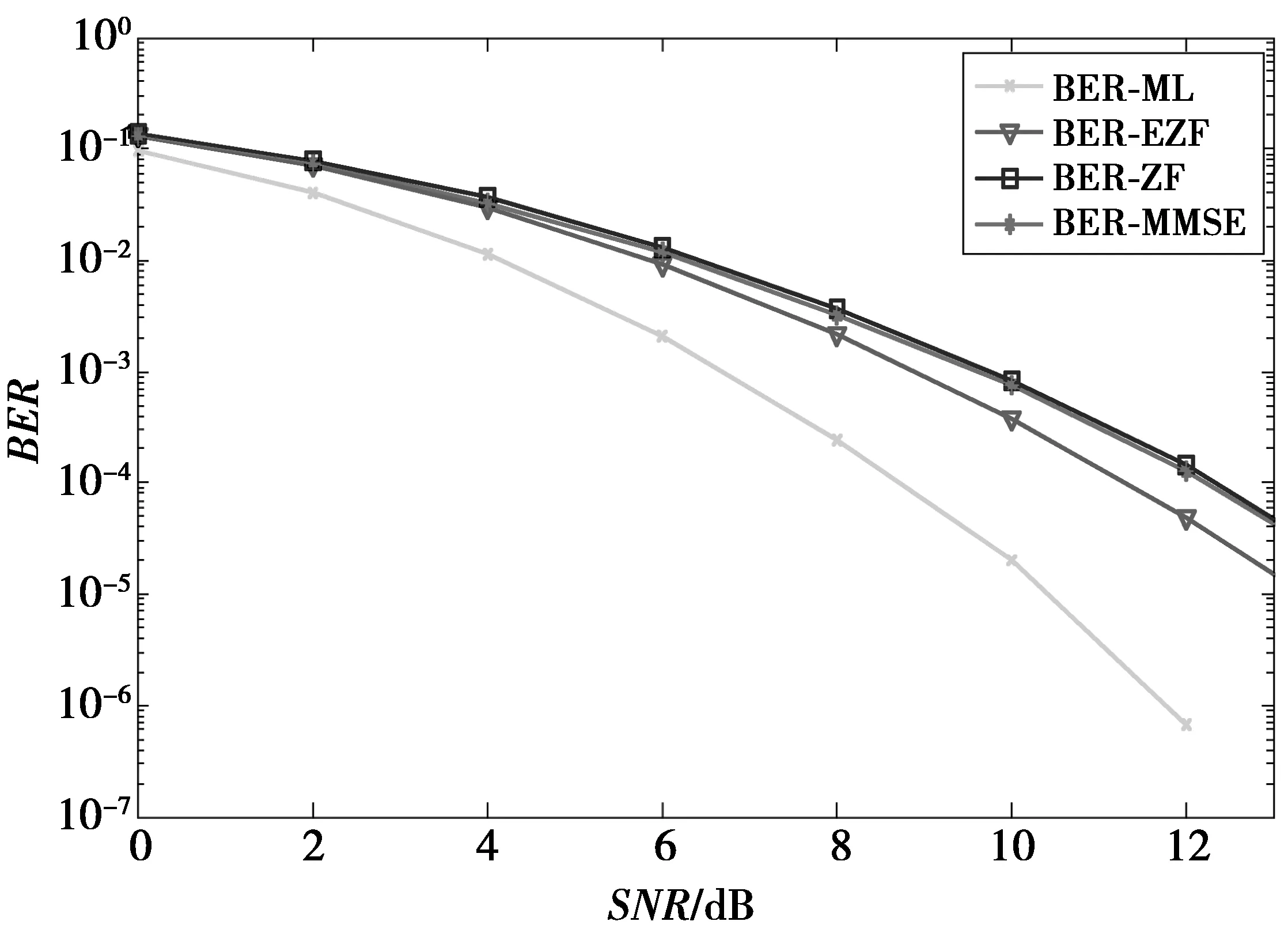
图3 Nt=4,Nr=8以及M=4(QPSK)下ML,MMSE,ZF以及EZF的性能比较Fig.3 Performance comparison between ML, MMSE, ZF and EZF with Nt=4,Nr=8 and M=4
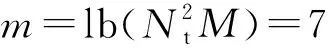
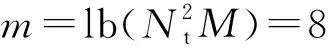
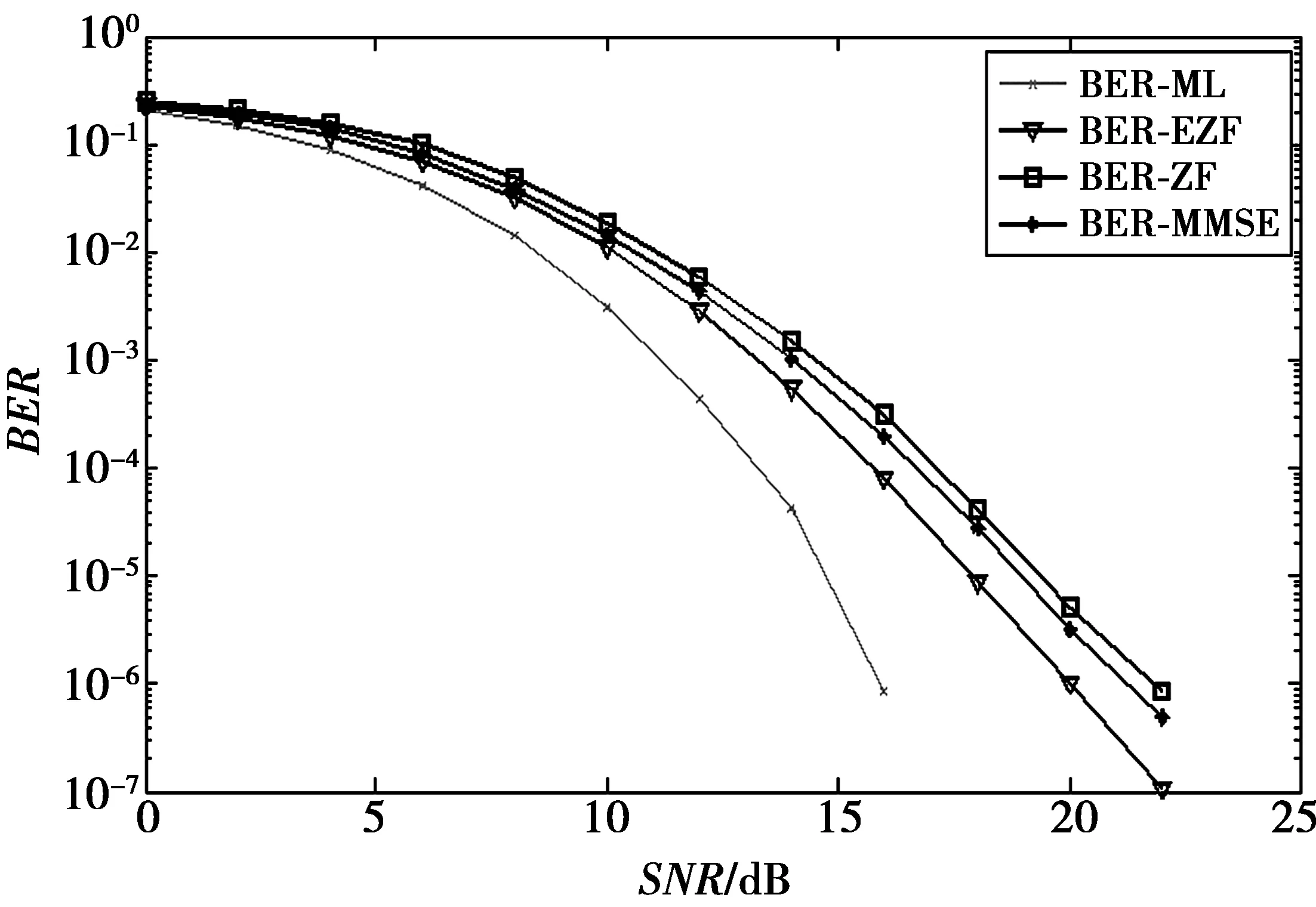
图4 Nt=4,Nr=8以及M=8(8QAM)下ML,MMSE,ZF以及EZF的性能比较Fig.4 Performance comparison between ML, MMSE, ZF and EZF with Nt=4,Nr=8 and M=8
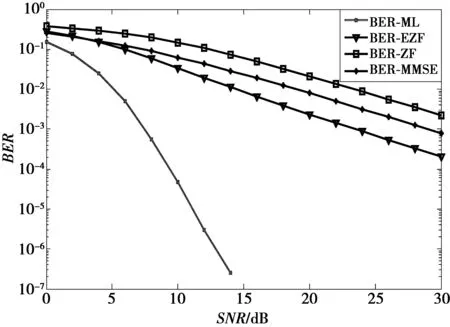
图5 Nt=8,Nr=8以及M=4(QPSK)下ML,MMSE,ZF 以及EZF的性能比较Fig.5 Performance comparison between ML, MMSE, ZF and EZF with Nt=8,Nr=8 and M=4
通过图3—图5可以看出,在不同的频谱效率下,提出的检测方案EZF能够实现较ZF和MMSE方案较优的性能。且EZF算法还实现了复杂度和性能之间的较好的权衡。
3.3 复杂度分析
迫零、最小均方误差、增强型迫零和最大似然4种检测算法复杂度如表3所示。从表3可以看出,EZF的复杂度比最大似然低,甚至比最小均方误差还低,仅仅比迫零略高。数值分析结果表明,EZF与ML相比,在复杂度上几乎可以降低70%。
4 结束语
本文针对正交空间调制系统不仅对传统的迫零和最小均方误差做了相应研究,并提出了一种有效的线性检测算法—增强型迫零。蒙特卡罗仿真结果表明,提出的检测算法与经典的线性检测算法相比有着较好的性能增益。与最大似然相比,提出的检测算法在复杂度上几乎可以降低70%,且复杂度甚至比最小均方误差还低,仅比迫零略高。
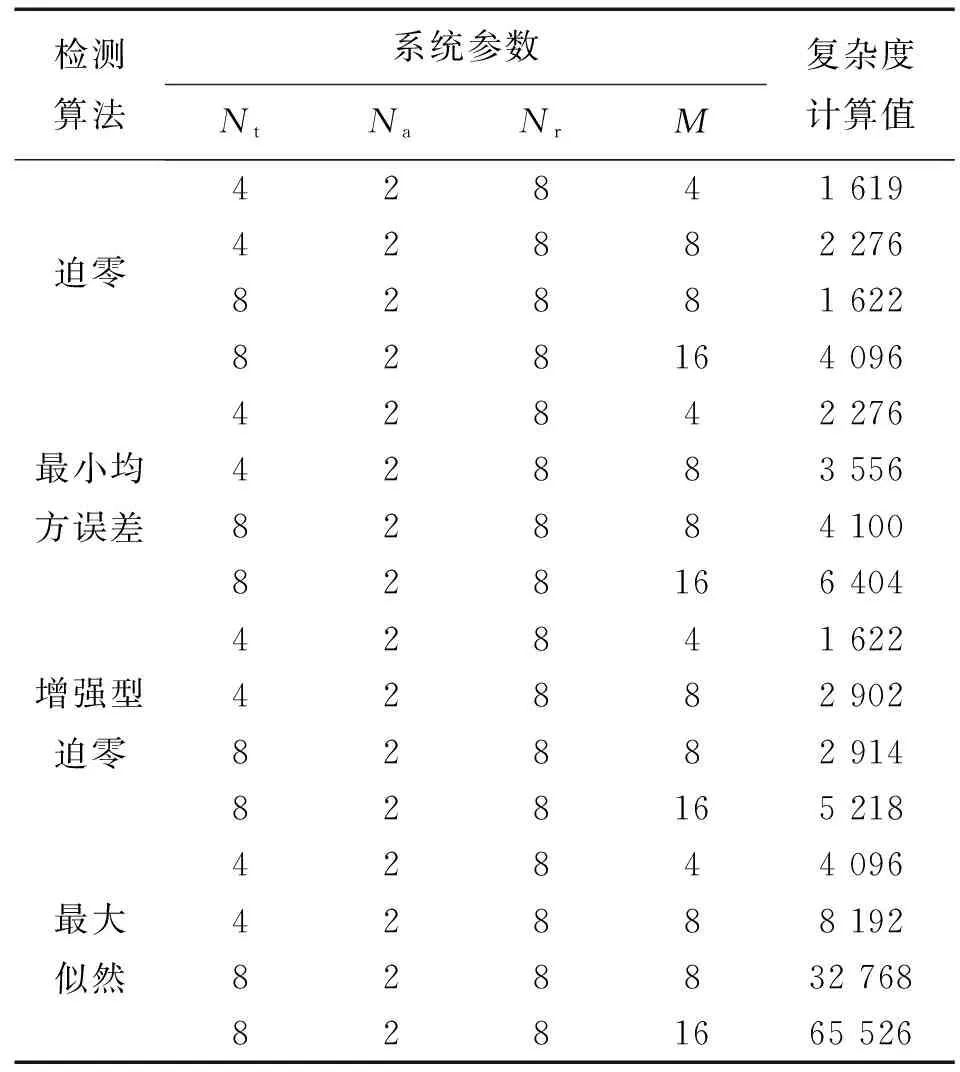
表3 不同检测算法复杂度的经典值
