一种用于电力线通信系统的改进MIMO检测算法

申 敏，李 想，林 欢

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.移动通信教育部工程研究中心，重庆 400065)

0 引 言

近年来，随着智能电网、物联网等技术的发展，电力线通信(power line communication, PLC)已逐渐应用于人们生产、生活等多个领域。与无线通信网络、传统的以太网等网络技术相比，电力线通信具有无需重复布线、分布范围广等特点，因此，电力线通信网络是一种具有较强竞争力的通信网络[1]。为了充分利用布线资源，将多输入多输出(multiple-input multiple-output，MIMO)技术引入电力线通信中，不仅能够提升整个系统的容量，而且能够提高覆盖范围和抗信道衰落的能力。目前ITU-T G.hn，IEEE1901和HomePlug AV2标准中已经采用了MIMO技术[2]。但是，MIMO PLC系统噪声环境复杂，噪声主要包括脉冲噪声和背景噪声，并且噪声之间存在相关性，严重影响通信质量，传统的基于高斯噪声环境设计的MIMO检测算法不能满足MIMO PLC系统的需求，因此，针对MIMO PLC系统中特殊噪声环境下的MIMO检测算法研究极具研究价值。

传统的MIMO检测算法主要应用在无线通信中，所有的算法设计均基于高斯噪声环境，其研究相对比较成熟。文献[3]提出的迫零检测算法通过消除信道影响来检测出发射信号，但未考虑噪声的影响，虽然复杂度低但性能不佳。文献[4]提出最大似然检测算法，该算法在高斯噪声环境下能获得最优的检测性能，但复杂度高，不便于工程应用。文献[5]提出一种次优的检测算法，将QR分解与球形译码(sphere decoding, SD)算法结合，牺牲一部分性能来降低信号检测算法的复杂度。上述算法都不适应MIMO PLC系统环境，所以，文献[6]提出用Alpha稳态分布建模脉冲噪声，采用基于分数低阶统计(fractional lower order statistics，FLOS)的检测算法，但该算法未考虑背景噪声以及噪声相关性，所以，Alpha稳态分布建模不具有一般性。

本文针对MIMO PLC系统特殊的噪声环境，采用了二元Middleton class A类噪声模型来描述脉冲噪声和背景噪声的联合分布，并考虑噪声之间的相关性。在此基础上对传统基于高斯噪声下的最大似然检测算法进行改进，通过二元Middleton class A类噪声分布得到在该噪声下的最大似然检测算法的表达式，改进算法在MIMO PLC系统中的性能明显优于传统的检测算法，无需再对脉冲噪声进行消除，可以直接根据噪声分布来检测。为了降低该算法的复杂度，本文进一步提出2种次优的检测算法，通过分段近似函数来降低指数运算的复杂度，且性能损失较小。

1 MIMO PLC信道模型和噪声模型

1.1 系统模型

家庭电力线路由相线(phase wire，P)，中线(neutral wire，N)和接地保护线(protection earth wire，PE)组成，这就为在家庭电力线通信中使用MIMO技术提供多端传输和多端接收的可能,但需满足基尔霍夫定律，故发射端只能采用2根天线[1]。文献[7]提出利用多导体传输线理论计算多输入多输出信道的衰减因子，利用多径模型计算单个载波信道的频率响应来建立多输入多输出电力线载波信道模型。MIMO PLC系统等效模型如图1所示。

图1 MIMO PLC系统模型框图Fig.1 Model of a MIMO PLC system

因为电力线上接入的负载不均，造成阻抗不连续，所以电力线信道具有多径效应和频率选择性衰落。多径信道模型为[7-8]

·e(-αm,n·dn)·e-j2πf(dn/vp)

(1)

(1)式中：m为发射天线序号；n为接收天线序号；N为多径数；gn为加权系数；dn为路径长度；vp为信号在电缆中传播速度；αm,n为衰减因子。

根据上述MIMO PLC信道建模方法，可以得到2×2的多输入多输出电力线载波通信共有4条信道，用矩阵表示为

(2)

MIMO PLC系统接收端接收信号为

Y=HX+N

(3)

(3)式中：Y为接收信号矩阵；H为MIMO PLC信道矩阵；X为发射信号矩阵；N为噪声矩阵。

1.2 噪声模型

电力线上噪声分为5类，包括有色背景噪声、窄带噪声、与工频异步噪的周期性脉冲噪声、与工频同步的周期性脉冲噪声和随机脉冲噪声。前3种称为背景噪声，后2种称为脉冲噪声。Middleton在1972年提出了一种脉冲噪声模型[9]。Middleton Class A噪声模型是一种非高斯分布的窄带噪声模型,包含相互独立的高斯分量和脉冲噪声分量的叠加，其背景噪声分布服从高斯分布，所以该模型能表示电力线上脉冲噪声和背景噪声的混合噪声环境。其概率密度函数表达式为

(4)

(5)

(5)式中，Γ表示高斯噪声功率与脉冲噪声功率的比值。

因为噪声之间存在相关性，文献[10]提出用二元Middleton class A噪声建模，该模型在Middleton class A噪声模型基础上加入了不同天线噪声相关性，概率密度为

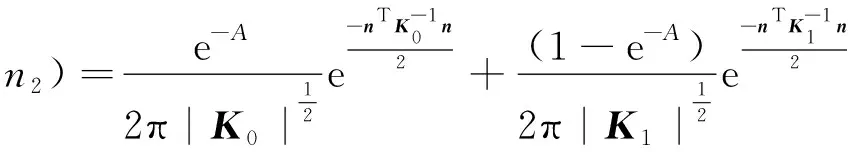
(6)

(6)式中：n1和n2表示不同天线上的噪声；Γ1，Γ2表示每根天线上高斯噪声功率与脉冲噪声功率的比值，Γ1,Γ2∈[10-6,1]；Km(m=0,1)为相关系数矩阵，即

，

(7)

(8)

(8)式中，K为相关系数，表示2根天线之间的相关度。

2 改进的最大似然检测算法

2.1 传统最大似然检测

传统的最大似然检测算法是基于噪声为高斯分布,最大似然检测是寻找最大化条件概率P(y|x)。其原理是将接收信号对所可能的发送符号域x遍历式的搜索，分析接收信号向量y和所有后处理向量Hx之间的最小欧式距离，把欧式距离最小的发送符号作为原始发送符号。

(9)

(9)式的搜索范围是整个星座图，当发送信号等概率时，概率函数可以表示为

(10)

(10)式等效为通过寻找接收信号与后处理的信号欧式距离最小的星座点来检测发射信号[4]。

(11)

(11)式中，ΩNt是标准星座点集合。

最大似然(maximum likelihood，ML)信号检测算法是目前最优的检测算法，能够获得最高的分集增益。目前ML算法主要应用在无线通信系统中，无线通信系统的噪声主要是高斯噪声，所以传统的ML算法是基于高斯噪声分布来实现。但是在MIMO PLC系统中，其噪声不再服从高斯分布，传统ML算法将不会提升性能。因此，本文提出在MIMO PLC系统噪声环境下的改进最大似然检测算法。

2.2 改进的最大似然检测算法

传统的最大似然检测算法中，可以遍历所有星座点来寻找在所有后处理向量中与接收信号欧式距离最小的星座点作为返回值。但是在MIMO PLC系统下的Middleton class A类噪声环境中，采用上述方式其复杂度非常大，所以只能根据Middleton class A类噪声的分布特性来得到改进的最大似然检测，当噪声最小的时候，其对应的概率密度函数值最大，这时能够检测出符号，噪声分布特性如图2所示。

(12)

f(y|x)的表达式为

(13)

(13)式中，n=y-Hx。

考虑噪声的实部和虚部是相互独立，且都服从Middleton class A类分布，(13)表达式变为

(14)

(14)式中：real (·)表示取实部；imag (·)表示取虚部。

图2 高斯噪声和Middleton class A类噪声概率密度函数Fig.2 Gauss noise and middleton class A noise probability density function

基于二元Middleton class A类噪声分布下的改进最大似然检测算法，虽然算法性能最佳，但复杂度高，为了便于实现，考虑在性能和算法复杂度间折中，提出2种次优的检测算法，可在性能损失较小的情况下，降低改进最大似然检测算法的复杂度。

2.3 2种次优检测算法

以上改进最大似然检测算法，其复杂度高的原因是因为指数运算和二次型运算带来的，所以次优检测算法可以通过降低指数运算的复杂度来降低算法复杂度。根据二元Middleton class A类噪声分布得到其似然函数，一般用对数形式表示

(15)

(15)式中，Λ1，Λ0和φ(z)定义如下

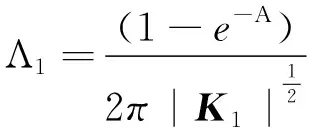
(16)

φ(z)=ln(1+ez)，∀z∈R

(17)

(17)式中，由于包含了对数运算和指数运算，使得其复杂度较高，针对该问题，本文提出2种次优的算法进行简化，降低改进最大似然检测算法的复杂度。次优算法通过分段线性函数来逼近φ(z)，性能上损失较少，但能够减少求对数和指数运算的复杂度，大大降低复杂度开销，如图3所示。

图3 近似函数与原函数对比Fig.3 Comparison of approximate function and primitive function

① 2段线性分段函数近似法。采用2段线性分段函数近似φ(z)。

(18)

该方法通过分段的线性函数降低了(14)式指数和对数运算，由图(3)可知，φ1(z)表示的折线能够基本近似φ(z)，因此，误差小，带来的性能损失相对较小。最终得到化简后的对数似然函数为

L(y|x)≈

(19)

(20)

图3表明，4段函数近似法能够与原函数曲线几乎重合，其性能损失能达到最小，该算法能够降低改进最大似然检测算法的复杂度，适用于MIMO PLC系统。最终表达式化简为

(21)

将(21)式代入(14)式，得到信号检测的表达式为

·imag (L(y|x))))

(22)

(22)式中，ΩNt是标准星座点集合。

3 复杂度和仿真分析

3.1 运算复杂度分析

本文对比分析了所提改进ML算法、2段近似次优ML算法和4段近似次优ML算法的复杂度，如表1所示。算法复杂度的变化主要是指数运算和对数运算，这3个算法都没有简化二次型运算的复杂度，所以，其二次型运算的复杂度不变，只简化了φ函数的计算复杂度。

根据(16)—(17)式得到z函数，其复杂度δ为

δz=Ο (23)

分析可知，2种次优ML算法较改进ML算法能降低一半的复杂度，大大降低了硬件实现的开销。

3.2 仿真结果分析

在Middleton class A类噪声环境下对本文所提算法进行性能仿真，验证算法的可行性。对比分析了基于高斯噪声分布的最大似然算法(ML)和迫零检测算法(ZF)以及本文所提改进最大似然检测和2个次优检测算法的性能。

噪声模型采用文献[10]提出的二元Middleton class A类噪声建模，如图1所示；信道模型采用文献[7-8]的MIMO PLC2×2信道，如图5所示，信道编码采用Turbo编码，具体仿真参数如表2所示。

表2 仿真参数

图4 脉冲噪声幅度Fig.4 Impulse noise amplitude

由图4可知，Middleton class A类噪声包括脉冲噪声分量和高斯噪声分量，脉冲噪声分量幅度高，若不考虑此噪声的分布或不采用脉冲噪声消除算法直接进行检测，系统性能将会受到严重影响。仿真中背景噪声用高斯噪声来替代。

图5表示信道采用多导体传输原理来建模，该信道是一个对称信道，包括共信道和交叉信道。MIMO PLC信道具有频率选择性衰减的特性，一般交叉信道的衰减相对共信道较为严重。由于本文主要是针对不同的MIMO信号检测算法对性能的影响，所以信道估计采用理想信道估计，忽略由信道估计误差对性能的影响。

图5 MIMO PLC信道频域响应Fig.5 MIMO PLC channel frequency response

图6对比了迫零检测、基于高斯噪声分布下的最大似然检测、本文所提的改进的ML以及2段近似次优ML和4段近似次优ML 5种算法的性能。仿真中噪声参数A为0.1，两天线的高斯噪声和脉冲噪声功率比分别为0.01和0.1，噪声相关系数为0.4。仿真结果表明，ZF和ML算法在QPSK调制下性能明显差于本文所提算法，主要原因是传统检测算法都是应用于高斯噪声环境，其具体实现都是基于高斯分布，但MIMO PLC系统的噪声环境不仅包括高斯噪声还有脉冲噪声，所以其性能差。而改进的ML检测算法基于MIMO PLC系统噪声模型，考虑了混合噪声模型，其性能好。改进的ML和2个次优算法在12 dB时，其误比特率已经达到10-5，其3种算法性能基本一致。从复杂度来分析，改进的ML虽然能够获得最佳的性能但其复杂度高，所以考虑实际应用，2种次优算法更具有实用性。

图6 QPSK调制下各个算法性能对比Fig.6 Performance comparison of each algorithmunder QPSK modulation

MIMO PLC系统若采用更高阶的调制方式，系统可获得更高的吞吐量，图7仿真了16QAM调制下的5种算法性能对比。仿真噪声参数A为0.1，两天线的高斯噪声和脉冲噪声功率比分别为0.01和0.1，噪声相关系数为0.4。分析可知，各类算法在16QAM调制下性能明显差于QPSK调制，因为高阶调制的容错能力较低阶调制差。但是本文所提的改进的ML算法和2种次优ML算法仍然比传统检测算法好，且这3种算法性能趋于一致。

图7 16QAM调制下各个算法性能对比Fig.7 Performance comparison of each algorithmunder 16QAM modulation

4 结束语

本文针对MIMO PLC系统特殊的噪声环境，采用二元Middleton class A类噪声建模，并对传统基于高斯噪声分布的最大似然检测算法进行改进，得到基于二元Middleton class A类噪声分布的检测算法，该算法能避免使用脉冲噪声消除算法带来的复杂度开销。为了进一步降低检测算法的复杂度，在此基础上提出2种次优算法，通过仿真验证均能获得良好的性能，从实际工程应用考虑，2种次优算法更能适应实际情况。