基于可靠性的服务功能链构建算法

兰巨龙，金子晋，孙鹏浩，江逸茗，王月

（国家数字交换系统工程技术研究中心，河南 郑州 450002）

1 引言

随着电子商务、数据中心、社交网络等新型网络业务的迅猛发展，目前的信息网络已难以承载不同用户的多样化需求[1]。传统 IP网络架构中，TCP协议通过校验和、确认应答和序列号、超时重传[2]等技术来保障数据传输的可靠性。然而这种方式容易造成数据分组的“粘连”，从而导致数据被截断或传输错误等后果，同时，超时重传的超时周期比较长，当数据分组发生丢失而采用超时重传技术进行恢复时，会增加大量传输时延。多协议标签交换（MPLS，multi-protocol label switching）作为IP网络的下一代传输技术，由因特网工程任务组（IETF，Internet engineering task force）提出。但是MPLS环境下网络管理难度大、可扩展性不足、成本高等问题仍然突出。尽管学术界和工业界针对数据传输问题研究开发了许多协议以及检测防护技术，但仍需面对数据流传输的可靠性问题。“为当前互联网设计新型体系结构是解决这些问题的根本途径”这一观点[3]得到学术界的一致认可。网络功能虚拟化（NFV，network functions virtualization）[4-5]等新兴技术应运而生，NFV不仅可增强网络服务的灵活性，而且有利于提升网络整体效能。在NFV中，基于软件的虚拟网络功能（VNF，virtual network function）[6]根据需求按一定的逻辑顺序组合构成服务功能链[7]（SFC，service function chain）来向用户提供相应的网络服务。VNF凭借其拓展性强、配置灵活且成本低等特性逐渐代替了传统的中间件盒子[8]。然而，网络服务的可靠性受网络功能的影响，网络功能故障导致的网络服务失效甚至网络瘫痪的事件时有发生。例如2012年12 月，谷歌公司因负载均衡器的配置不当导致包括 Gmail和 Chrome 在内的多个谷歌服务受到影响[9]。因此，如何提高服务功能链的可靠性成为近年来研究的热点。

对此，文献[10]通过对 SDN/NFV（software defined networking/network functions virtualization）技术的分析，提出通过组合虚拟安全应用模块来构建安全服务链（SSC，security service chain）的技术思想，但并未给出服务构建策略。文献[11]基于软件定义网络环境提出一种灵活可配的安全服务链动态组合机制，但未考虑多节点协同组合的情况。文献[12]在假设网络节点具有安全服务能力的条件下，研究了节点间的路由问题，提出一种多点到点的节点树路由算法，在算法所得解中单个交换机路由规则的最大数量是有界的且与网络大小一致。该算法复杂度低，可在动态网络环境下应用，但是在可靠性保障方面效果并不突出。文献[13] 提出了一种基于 NFV环境的数据中心网络可靠性感知延迟约束路由优化框架READ（reliability-aware and delay-constrained），采用一种复杂的混合整数线性规划来得到一个最优的VNF部署和路由策略，以最大限度地保障数据传输可靠性；同时，提出了启发式算法—— GSP来降低算法的复杂性并获得有效的路由方案，然而该算法对复杂度的降低效果仍有待提高。

在现有的研究基础上，本文侧重于节点间的路由选路问题，在每个流所需的服务都被实现且网络节点具有安全服务能力的情况下（即不考虑容量、带宽等条件的限制），提出一种新的选路算法。首先，排除部分冗余事件来确定路径失效的上下界；其次，引入多个新的指标，量化节点的失效概率，将失效概率转化为长度；最后采用最短路径算法来进行网络节点间路由的可靠性分析，从而给出确切的选路方案。

2 模型

考虑一个与文献[12]中相同的网络拓扑，如图1所示。

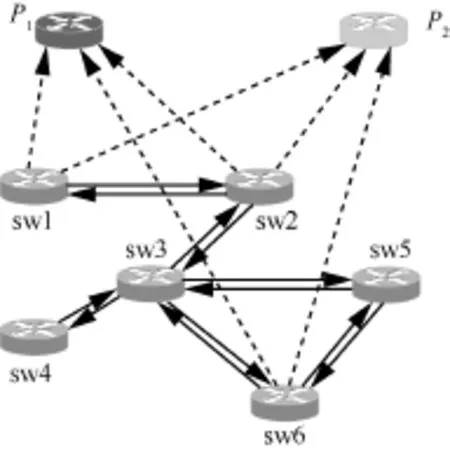
图1 网络拓扑

为了方便模型的建立及表述，本文将这一拓扑抽象为图2形式，其中，实心点表示网络节点（下文中简称为节点），空心点表示为其提供服务的底层（PM，physical machine）（下文中简称为底层节点）。假设每个底层节点为节点提供的服务是可取代的（可以理解为一个或多个可提供服务的备份底层节点），则只要有至少一个底层节点向其提供服务，节点就能发挥功能。

图2 模型示意

3 路径可靠性的计算

假设p为底层节点失效的概率，n为节点数，如果每个节点都只有一个底层节点为其提供服务，则路径失效的概率为然而，若每个节点拥有提供服务的多个底层节点，计算路径失效的概率是一个NP-hard问题[14]。不过，仍然可以通过一个（,ε δ）近似算法来估算路径的失效概率。对于最小化问题，首先给出最优解的一个下界，然后把算法的运行结果与这个下界进行比较。最大化问题则先给出一个上界然后把算法的运行结果与这个上界比较。文献[15]中的蒙特卡洛算法证明，在此背景下路径失效的概率为其中，E[I]是I的期望值，当循环次数足够多时，E[I]可以被近似地估算为1-δ。

如果每个节点拥有相同个数底层节点，且每个底层节点失效的概率一致，则抽取节点vi的概率为如果节点v被选中，将其拥有的底层节点全部

i设为失效；对于其他的底层节点，仍然遵循其自身的失效概率。定义U为所有失效底层节点的集合，当且仅当U中底层节点失效时，测试vi是否为中第一个失效的，若是，定义I=1,若不是则I=0。对这一过程重复次，然后计算路径失效的概率为具体步骤如算法1所示。

如果采用蒙特卡洛算法[16]，当路径的失效概率太低时，迭代的次数会非常庞大，而采用重点抽样的方法进行估算，会使迭代次数减少。

算法1重点抽样算法

初始化

主循环

结果

然而，算法1只能估算某条特定路径的失效概率，并不能用来寻找最可靠的路径。因此，下文会引入新的指标，来寻找最可靠路径。

3.1 底层节点失效概率小且相同

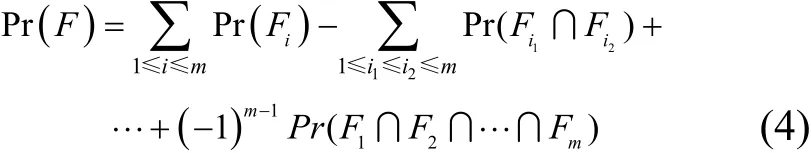
其中，Pr（x）表示事件x发生的概率。由于容斥公式的第j项有项求和，直接计算路径失效概率是很困难的。因此，需要减少式（4）中的项数，并根据底层节点的失效概率小且相同这一条件，进一步简化计算。

为了减少式（4）中的项，首先需要去除一些冗余事件。例如，若事件iF发生当且仅当事件Fj发生，那么事件iF就是冗余的。定义当事件iF冗余时，节点vi为可移除节点，为节点vi所独有的底层节点个数。

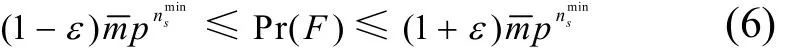
证明

定义集合A为除多余节点以外的节点；1A⊂A为集合A中恰好拥有个底层节点的节点，则为剩余节点的集合，其中每个元素 拥 有ns

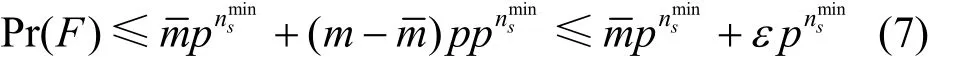
min+1或者更多个底层节点，则可得当时，Pr（F）的上界为对于A中的任意一对节点拥有的底层节点数至少有个，因此，至少需要移除个节点来使1A中的一对节点失效；至少需要移除ns

min+2个节点来使A2中的一对节点失效，则可得时，Pr（F）的下界为

证毕。

另外，如果每个节点都拥有ns个不同的底层节点，每个底层节点的失效概率为且不相关，那么路径失效的概率满足

证明

若节点vi和vj拥有相同的底层节点，那么必同时失效且因此，在计算路径失效概率时，这些拥有相同底层节点的节点可以用一个节点来代替。定义为路径中的节点，其中它们的底层节点至少有一个不相同，则式（4）中的第一项可转化为又节点一共拥有至少个底层节点，则这2个节点同时失效的概率为对于式（4）中的第2项，有

3.2 底层节点失效概率随机

当底层节点失效的概率随机时，计算路径失效的概率十分困难，因此，本文首先对路径的失效概率范围进行限定，然后寻找最可靠的路径。

3.2.1 路径失效概率上界

证明

定义事件S为节点有效，如果节点vi及∪kvk没有共用的底层节点，那么事件Si即节点vi有效与事件Sk即节点∪kvk有效是不相关的；相反，若节点vi及∪kvk共享了一个或者多个底层节点，那么事件与事件相关。因此

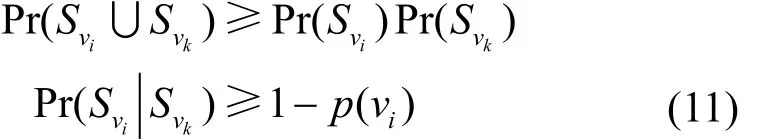
证毕。

3.2.2 路径失效概率下界

首先，将为多个节点提供服务的底层节点替换为多个独立的新的底层节点，每个新的底层节点只为一个节点提供服务，显然，这不影响原路径的失效概率。对图，考虑节点为节点vi的底层节点，其中Bi为节点拥有的底层节点的集合，为其失效的概率，定义为由提供服务的节点数目，完成替换后，底层节点的失效概率为

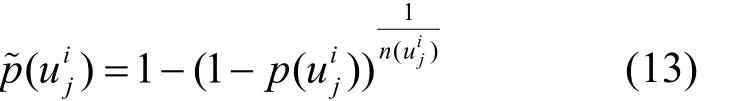
若底层节点失效的概率不相关，则节点vi失效的概率为

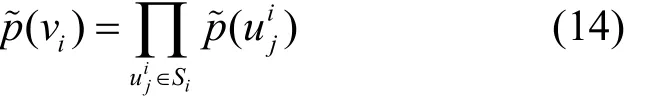
由此，可得路径失效概率的下界为

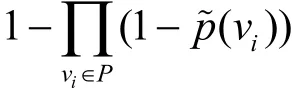
其中，P为路径上节点的集合。

证明[17]

定义BP为路径P中节点拥有的底层节点集合，为由底层节点提供服务的节点集合，且

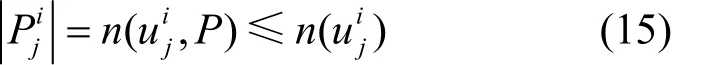
同时，定义Bs为所有有效节点（即所有服务层节点及底层节点）的集合，Bf为所有失效的节点的集合，则若路径P中每个节点拥有的底层节点至少有一个在集合Bs中，那么路径P连通，不论底层节点是否失效；若路径P中某一节点所拥有的所有底层节点都在集合Bf中，则路径P失效，不论底层节点是否失效；若路径中节点除外的其他底层节点都失效，则路径P连通当且仅当有效。用个独立且失效概率为的节点来代替那么所有个节点都有效的概率为

对每个底层节点都采用上述操作，最终，可以得到路径失效概率的下界为

证毕。

4 最可靠路径的选择

4.1 底层节点失效概率小且相同

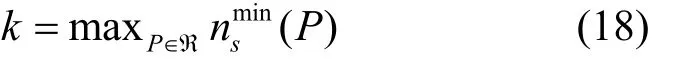
将拥有底层节点数小于k的节点以及与其相连的边都移除，得到一个新的图显然，为了使路径的可靠性最高，被移除的节点在选路时并不会被用到。定义V′′V′⊆ 为拥有k个底层节点的节点，则本文的目标是找到一条路径P，定义其包含节点的集合为VP，使VPV′′∩ 最小。定义Si为节点iV′′∈ 拥有底层节点的集合，定义一个变量xij，xij=1，当且仅当边（i,j）

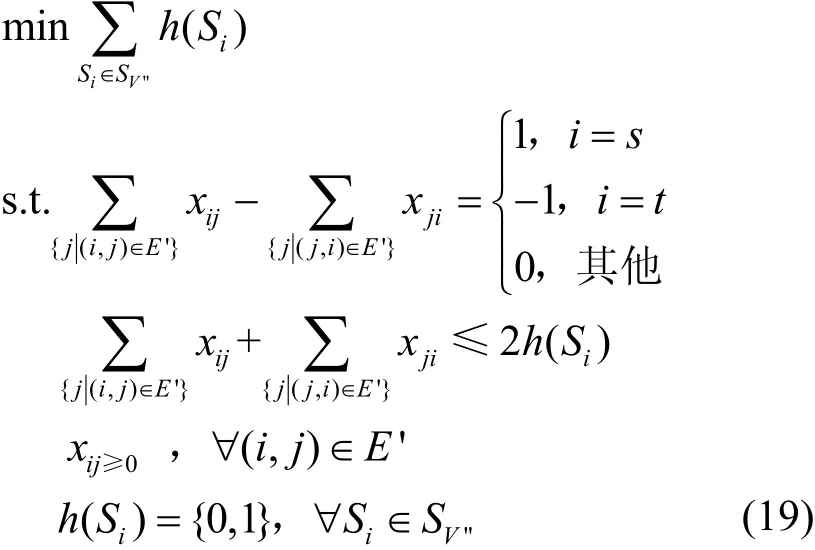
算法2选路算法

4.2 底层节点失效概率随机

如前文所述，可求得某一路径失效的上下界。在本节中将那些为多个节点提供服务的底层节点替换为多个独立的新的底层节点，从而将一个寻找最可靠路径的问题转化为一个标准的最短路径问题。由此，本文提出以下算法，用以估算路径失效的概率。对于vi∈V，定义为节点vi的失效概率，底层节点的失效概率为其中，底层节点为个节点提供服务

同时，假定vi失效的概率独立且为将穿过节点vi的距离设为那么，寻找最可靠路径的问题可以转化为一个标准的最短路径问题。具体步骤如算法3所示。

算法3s-t路径可靠性估计算法

5 仿真计算

对本文提出算法进行模拟选路，并对算法可靠性、算法实现所需时间等指标进行仿真评估，同时与其他算法进行比较。本文仿真环境为Win7操作系统，CPU型号为Core i7-4710HQ，主频2.50 GHz。在仿真时，如果最可靠路径受到容量带宽等条件的限制无法实现，将自动选择次优路径。采用mininet工具搭建一个如图3所示的网络拓扑，其中横轴表示经度，纵轴表示纬度，*表示网络节点， 表示底层节点，网络拓扑由37个节点和52条边组成，其中，s表示源节点，t表示目的节点。

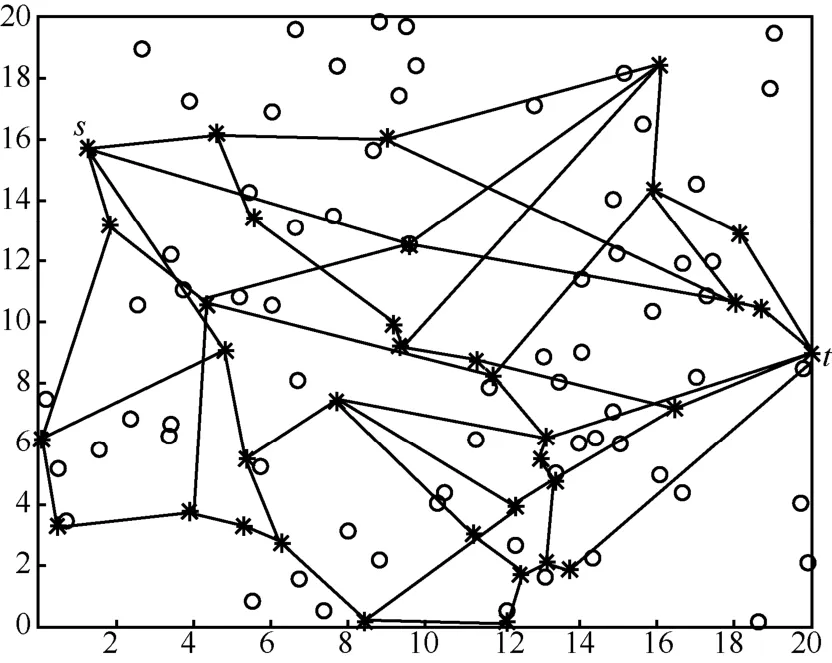
首先，假设每个节点都由离它最近的2个底层节点提供服务，每个底层节点失效的情况独立且概率为1%。由于底层节点失效概率很小且相同，所以可以通过算法2获得最可靠路径。

图4 最终链路选定

在与文献[12]算法和文献[13]算法进行对比时，本文对扩大样本进行了大量实验，实验都采用50个点的拓扑，对比结果如图5所示。由图5可知，与文献[12]算法相比,本文中算法2的路径选择可靠性的提高了 15%以上；而与文献[13]算法相比，算法2在可靠性保障方面也有所提升。

图5 各算法可靠性对比

在实验过程中，针对底层节点失效概率小且相同的情况，最可靠路径的选择可在5 s内完成；对于本文中算法2的近似求解可以在1 s内完成；而对于算法 3，采用启发式算法得到的路径的选择需要几秒钟来实现。相信在更为专业的实验环境下，本文算法能得到更快的实现。同时，在对文献[12]算法与文献[13]算法的实验进行复现时，所得实验时间如图6所示，从图6中可知，本文算法实现所需时间较另2种算法均有大幅减少。因此，本文算法具有一定的实际应用价值。

图6 不同算法所需时间对比

6 结束语

目前的信息网络已难以承载不同用户的多样化需求，针对这一现状，本文基于目前发展日新月异的NFV环境，提出了一种多点到点传输的路径可靠性算法。该算法对服务功能链的选定进行量化分析，从而满足用户对于服务功能链的可靠性需求，性能指标提升较大且算法实现所需时间较少。目前，有关网络服务功能链部署问题的研究正不断兴起，下一步将继续完善本文研究，在考虑资源、带宽等方面影响的情况下，从多个方向完善服务功能链可靠性的研究。