基于结构相似性的非参数贝叶斯字典学习算法

董道广，芮国胜，田文飚，康健，刘歌

（海军航空大学信号与信息处理山东省重点实验室，山东 烟台 264001）

1 引言

字典学习是图像和通信信号处理方面的重要内容，是进行信号和图像数据分类[1]、压缩[2-6]、去噪[7-11]、修复[7,9-10,12-13]乃至超分辨[14]的有力工具，随着我国太空战略的深入推进，字典学习在海洋信息感知领域，尤其在卫星图像遥感、卫星气象遥感、卫星军事侦察等方面的应用价值愈发凸显。近年来，非参数贝叶斯方法在字典学习中的应用引起人们的关注，相对于以最优方向法（MOD, method of optimal directions）和K奇异值分解算法（K-SVD，K-singular value decomposition）为代表的传统综合字典学习算法体现出了显著的优越性。该优越性体现在三方面：1）学习过程中能够自动推断出字典原子数目、信号稀疏度和正则化参数值，从而无需对这些参数的取值进行预设，避免了因预设不当而造成的人为影响；2）有严格的理论证明其算法的收敛性和解的最优性，而K-SVD和MOD尚缺乏理论证明的支撑；3）其自身基于概率图模型进行建模，结构清晰且具有开放性，适于引入各种正则化概率先验约束。

Zhou等[11]将非参数贝叶斯用于图像去噪和压缩重构，提出了 beta过程因子分析（BPFA, beta process factor analysis）算法，是贝叶斯因子分析方法在字典学习领域的一次成功尝试，取得了较好的应用效果，但该算法没有考虑到图像的全局结构相似性和变异性，在字典结构特性方面仍有较大提升空间。后期围绕提升非参数贝叶斯字典学习的结构特性，又陆续出现了狄氏过程-beta过程因子分析（DP-BPFA，Dirichlet process-beta process factor analysis）[7]和相依分层 beta过程（dHBP，dependent hierarchical beta process）[9-10]等算法，这些算法将空间相关性引入了非参数贝叶斯建模，使图像在字典学习下的稀疏表示能够体现出一定的邻近空间相似性，显著提升了字典在去噪、修复、压缩感知等方面的应用性能，但复杂度颇高，运行时间较长。Sunil[15-16]及 Li[17-18]等认识到结构相似性和变异性对信号/图像稀疏表示的重要影响，基于狄氏过程的聚类特性，提出了适于多来源数据条件下的多字典学习算法，较好地解决了图像稀疏表示对结构相似性的利用问题。但数据聚类的先验建模用到了stick-breaking模型，因其非共轭的数学形式，造成了后验推断上的非解析性。其次，多字典学习适于数据来源非单一的情形，对于单一来源数据内部结构的聚类效应，其适用性仍值得进一步研究。在传统的结构字典下，图像的稀疏表示具有块结构性，这利于提高字典对信号结构特征的表达能力，且相似图像块稀疏表示的支撑集通常也相似，利于进行多观测向量模型下的联合稀疏重构，进而利于降低观测数目并提高重构性能。这为非参数贝叶斯字典学习提供了重要的启发，即将字典学习建立在图像块相似性聚类的基础上，并进一步将块结构特性引入稀疏表示作为字典学习的正则化约束条件。而非参数贝叶斯字典学习则因其对图像本身结构的自适应性，继续保持其相对于传统结构字典的优势。

本文在上述问题和解决思路的启发下，提出了一种基于结构相似性的非参数贝叶斯图像字典学习算法，其主要创新有三方面：1）以图像块的相似性为测度，通过K-均值分类算法对图像块进行聚类处理，将前述各非参数贝叶斯字典学习算法的空域结构特征从局部扩展到全局，使所有具备相似结构的图像块共同参与本聚类图像块的稀疏表示；2） 鉴于传统结构字典下多个相似信号联合稀疏重构时一般假设支撑集相同的局限性，为使相似图像块的稀疏表示适应支撑集平滑变化的实际情况，令同一聚类内部的各图像块对字典原子的使用仅服从概率意义上的相同，使得学习所获得的字典利于进行多信号的联合稀疏重构；3）将传统结构字典下信号稀疏表示普遍存在的块结构效应作为正则化约束条件引入非参数贝叶斯字典学习框架，以提升字典对图像结构的表达能力。

2 贝叶斯建模

2.1 基于全局结构相似性的图像预处理

图像内部存在大量的相似冗余成分，其在传统结构字典下的稀疏表示也具有相似性，突出体现为支撑集的相似性。将全局相似性测度引入字典学习框架有利于提升字典对图像结构特征的表达能力。本文采取K-均值聚类方法进行图像块聚类。K-均值聚类是一种简单而又行之有效的无监督聚类方法，在数据未分类亦无标签的条件下，依预设的聚类数目随机选择相应的聚类中心，通过计算各图像块到各聚类中心的相似性测度，决定图像块的聚类归属，随后将各聚类内部全部图像块的均值作为新的聚类中心，再次计算各图像块到各聚类中心的相似性测度，进行新一轮的聚类。迭代执行上述过程，直至各聚类中心相对前次迭代的聚类中心无明显偏移或达到预定迭代数目上限时，方结束迭代并输出最终聚类结果。其中最为关键的2个问题分别是聚类数目的确定和相似度测度的选择。聚类数目过多会造成聚类顽健性下降，出现聚类碎片效应，对字典学习造成不利的人为影响；但也不宜过少，因为过少会无法准确体现自然图像中丰富的结构信息。本文以图像块灰度值的欧式范数作为相似性测度，并根据聚类分割中常用的贝叶斯信息准则（BIC，Bayesian information criterion）确定聚类数目。

2.2 非参数贝叶斯字典学习建模

设从图像中采集了N个P×P灰度块，对其分别做列向量堆栈处理，记作其中M=P×P，i= 1,2,… ,N。此时经过前述聚类操作，此时的数据集是带有聚类标签的，这将为后续的字典学习提供重要的结构参考。待学习的字典记作，由K个与xi同维数的原子构成。虽然不需要预置字典原子规模是非参数贝叶斯的一大优势，但这与K值的选择并不矛盾，因为非参数贝叶斯字典学习的核心思想是贝叶斯稀疏因子分析，稀疏先验可以确保信号表示的稀疏性，在K值足够大的条件下，仍会存在相当数量的原子不参与对信号的表示，很容易确定实际的原子规模。本文算法的核心即基于聚类处理后的数据集和下述非参数贝叶斯模型估计获得字典D。数据观测模型为

其中，i表示当前图像块在采集到的全部图像块中的位序；是稀疏表示的权重分量，反映各原子参与表示信号的程度；是稀疏表示的模式分量，反映各原子有无参与对信号的表示；符号⊙是Hadamard乘积，即逐元素对应乘积而不改变向量维数；iε是均值为0的高斯白噪声，其中0α是观测噪声精度，服从Gamma超先验分布，如式（3）所示。

该分布与高斯分布共轭，a和b分别表示形状参数和尺度参数，为保证噪声幅值的稀疏性，一般取

式（1）中，当zi的某个元素zik= 0时，sik便不再起作用，因为原子dk并不参与对xi的表示。权重向量si服从如式（4）所示的多元高斯先验分布。

其中

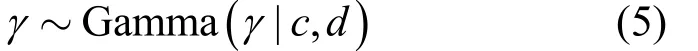
出于防止过拟合的考虑，令权重向量的全部元素使用相同的逆方差γ。类似地，Gamma分布的参数一般取

与基于BPFA的算法相比，本文所提算法将前述聚类过程获得的全局相似性结构特征引入到稀疏模式向量zi的先验分布中，如式（6）和式（7）所示。

其中，πjk是聚类j中原子dk参与表示数据的概率，J是聚类数目。

假设同一聚类内部的数据对字典原子的使用概率是相同的，允许这些数据不必共用同一支撑集，而是仅在概率意义上具备支撑集的同一性，从而适应了自然信号在空域和时域上普遍存在的支撑集缓变特性。需要指出的是，假设当前数据所属聚类标签为j，该聚类内全部数据索引的集合记作则超参数

eˆ和的取值决定于该聚类中全部数据稀疏模式向量相应元素的毗邻元素取值。引入符号该符号代表花括号内集合的元素总数；代表集合的元素总数，并分别定义变量1Δ、2Δ和3Δ，如式（8）～式（9）所示和的取值规则如式（11）所示。

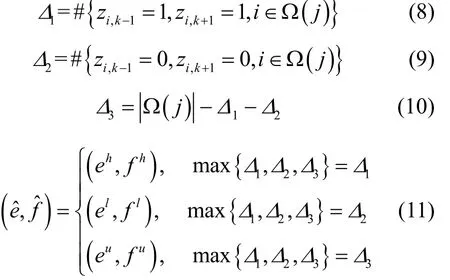
式（8）～式（11）的核心即将马尔可夫随机场的思想引入字典学习框架中。当邻域稀疏模式均为1时，取值为1的概率更大，令有利于生成数值较大的πjk，从而倾向于使zik以较大概率取值为1；当邻域稀疏模式均为0时，zik取值为0的概率更大，令有利于生成数值较小的πjk，从而倾向于使zik以较大概率取值为0；当邻域稀疏模式为1和0共存时，zik具备取值的不确定性，此时令可以保证z取值概率的均衡性。

ik

然而，有别于各数据向量具有不同原子使用概率的情形，也有别于所有数据向量共用同一原子使用概率的情形，全局结构相似性聚类后的数据在同一聚类内共用相同的原子使用概率，这是对zik取值的折中处理，也是结构聚类思想的本质要求，为此，需统计聚类内部各数据向量的邻域稀疏模式，以数量最多的邻域稀疏模式决定的取值，如式（11）所示。字典原子服从如式（12）所示的高斯先验分布。

基于上述理论，建立贝叶斯建模的概率图模型，如图1所示。

图1 贝叶斯建模的图模型

3 贝叶斯推断

3.1 原子dk的Gibbs采样

结合式（1）观测数据模型和式（12）原子先验分布，可得的dk满条件分布，如式（13）所示。

其中

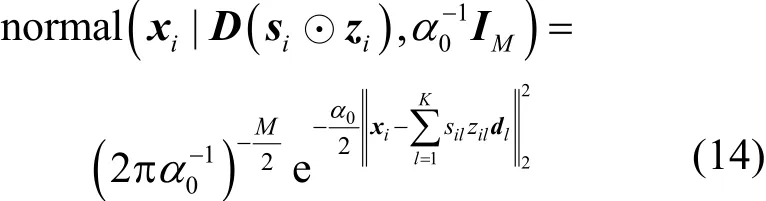
3.2 权重si的Gibbs采样

结合式（1）观测数据模型和式（4）权重先验分布，可得的sik的满条件分布，如式（18）所示。

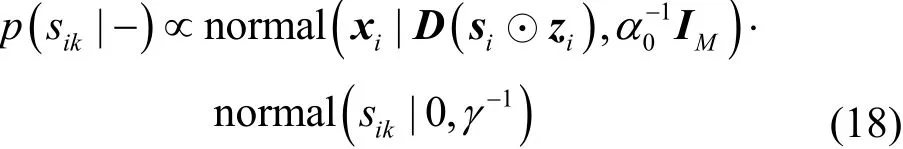
整理可得

3.3 稀疏模式zi的Gibbs采样

结合式（1）观测数据模型与式（6）稀疏模式先验分布，可得zik的满条件后验分布，如式（22）所示。

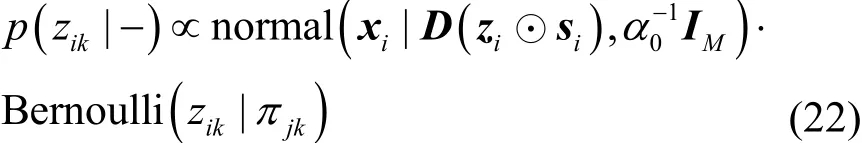
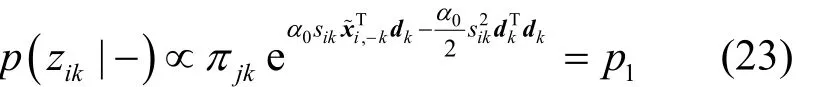
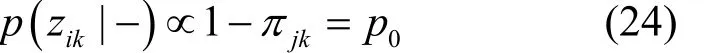
整理可得zik的满条件分布为Bernoulli分布，即

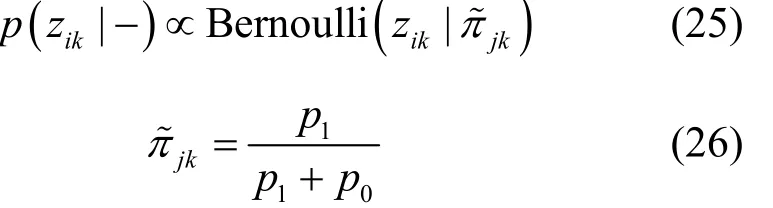
3.4 原子使用概率π的Gibbs采样

结合式（6）和式（7），可得πjk的满条件分布，如式（27）所示。

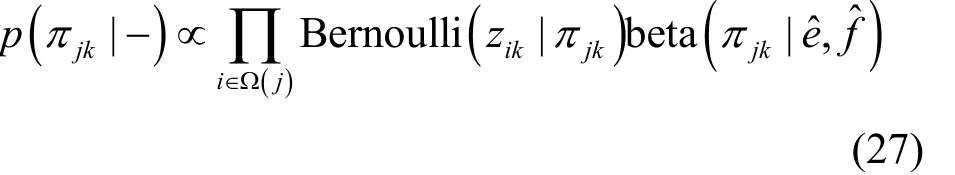
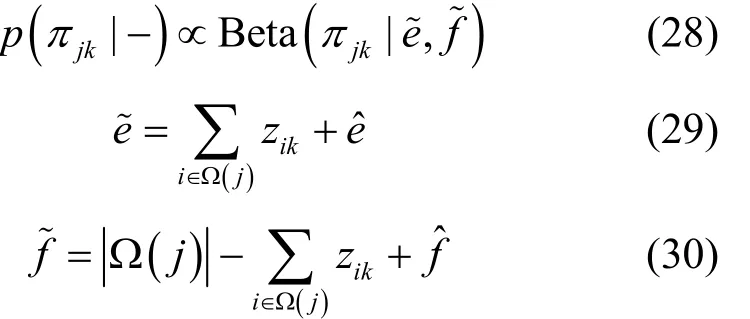
3.5 超参数0α和γ的Gibbs采样

结合式（1）和式（3），可得超参数0α的满条件分布，如式（31）所示。

整理可得

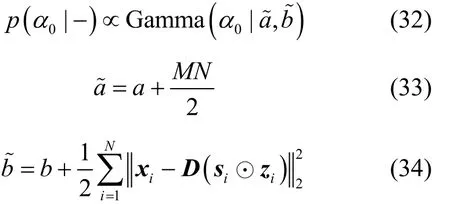
结合式（4）和式（5），可得超参数γ的满条件分布，如式（35）所示。

整理可得

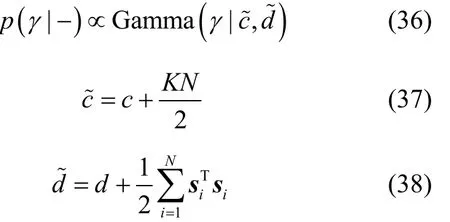
根据式（32）～式（34）可对超参数0α进行Gibbs采样，根据式（36）～式（38）即可实现对超参数γ的 Gibbs采样。

迭代执行本节的Gibbs采样流程，直至达到预定数目的迭代上限，即结束迭代并输出各隐变量和模型参数的当前采样值作为推断结果，完成字典学习，本文与传统BPFA保持一致，将迭代次数上限设置为 150，为免混淆，本文算法称为结构相似性beta过程因子分析（SSIM-BPFA，structure similarity-beta process factor analysis）算法，具体流程见算法1。

算法1SSIM-BPFA字典学习算法

输入图像块数据集

初始化超参数当图像大小超过300×300时令字典原子规模K=512，否则令K=256。

步骤1利用K-均值算法结合传统的BIC准则对进行聚类预处理，确定聚类数目J，并获得每个数据点的聚类标签j，j=1,…,J。

步骤2根据式（1）～式（12）进行贝叶斯概率建模，建立隐变量和模型参数集

步骤3设置迭代总数为150，为当前迭代索引赋值t=1。

步骤4按照式（15）～式（17）对字典原子进行Gibbs采样。

步骤5按照式（19）～式（21）对权重进行Gibbs采样。

步骤6按照式（23）～式（26）对稀疏模式进行Gibbs采样。

步骤7按照式（28）～式（30），并参考式（8）～式（11）对原子使用概率进行Gibbs采样。

步骤8 分别按照式（32）～式（34）和式（36）～式（38）对超参数0α和γ进行后验Gibbs采样。

步骤9 若t=150，则将Θ内各元素的当前采样值作为估计值；若t≠150，则令t=t+1，并返回步骤4执行迭代。

输出当前估计的字典，权重和稀疏模式

4 算法分析与数值实验

本文围绕图像去噪和压缩感知这 2个方面的性能对所提的 SSIM-BPFA算法的有效性展开评估，以图像处理领域中的Barbara、Lena、Boath、House和Peppers图像的灰度值作为实验对象，使用Matlab编程进行数值实验。

4.1 去噪实验及性能评估

以分辨率512像素×512像素的图像Barbara为例，采用滑窗分块方式将其分割为255 025个具有重叠的8像素×8像素分辨率的图像块，并对全部图像块的灰度值进行列堆栈处理，构成算法执行所使用的数据集。按照SSIM-BPFA算法的流程进行字典学习，并将初始字典原子数目设置为512 个，训练所得字典如图2所示。

图2 SSIM-BPFA算法训练所得图像字典

设噪声标准差σ=25，采用SSIM-BPFA算法对Barbara进行去噪处理，结果如图3所示。可见相比于图 3（b）所示的含噪图像，图 3（c）所示的去噪图像的峰值信噪比（SNR，signal noise ratio）显著提高，图像视觉效果也得到了明显的改善，而且运行时间较BPFA算法并未有明显的增加。

图3 SSIM-BPFA算法去噪实验结果

为进一步验证 SSIM-BPFA算法的性能，除Barbara外又增加了Lena、Boat、House、Peppers等作为实验图像，并引入MOD、K-SVD、传统的离散余弦傅里叶变换（DCT，discrete cosine transformation）等传统的字典学习算法与本文的SSIM-BPFA算法进行比较。实验过程中，分别采用噪声的标准差为5、10、15和25这4种参数进行实验。实验结果显示，噪声标准差等于5、10、15时7种算法的去噪结果与表1相似，只是在噪声标准差较大时对比更为显著。因此，本文以为例，对比了SSIM-BPFA和其他6种算法对实验图像去噪处理后的峰值信噪比结果，如表1所示，表中的实验结果是进行50次实验后，实验结果的平均值。

由表1可知，SSIM-BPFA的去噪峰值信噪比明显高于其他 6种算法，其中 BPFA、DP-BPFA和dHBP这3种算法的去噪性能相近，这与Zhou的研究结论是一致的[7]。

4.2 压缩感知实验及性能评估

利用前述去噪过程中7种不同算法分别学习获得的字典，结合相应的压缩感知算法，对经观测矩阵降维投影后的图像数据进行重构。Zhou[7]的研究已经证实了BPFA算法相对其他字典学习算法在压缩感知应用中的优势，所以限于篇幅，本节实验着重对SSIM-BPFA算法所得字典与BPFA、DP-BPFA和dHBP这3种算法所得字典进行压缩感知性能对比。为便于比较分析，仍以Barbara作为实验对象，出于克服块结构效应的重构需求，实验数据的生成方式仍采用4.1节的滑窗法。由于前述字典学习过程中，图像块在字典表示下的稀疏度普遍不超过4，故出于提高重构成功概率的目的，本节实验选择的投影观测矩阵行数以8为下限，设置了行数分别为8、10、12、14、16、18等共6种观测数目作为实验条件，所用投影观测矩阵的元素独立同分布地采样自标准正态分布。

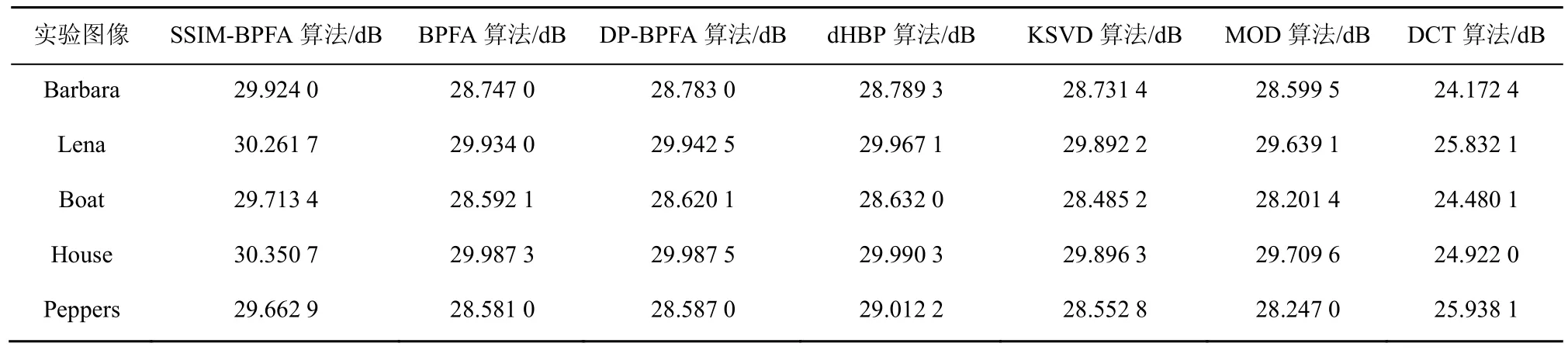
表1 不同字典学习算法的图像去噪峰值信噪比

图4所示即观测数目为8时，压缩感知经典的正交匹配追踪（OMP，orthogonal matching pursuit）算法分别在 SSIM-BPFA算法、BPFA算法、DP-BPFA算法和dHBP算法所得字典下对Barbara的重构结果及相应的峰值信噪比。由图可见，图4（d）在视觉效果和峰值信噪比方面均显著优于图 4（a）～图4（c）。在Lena等其他4幅实验图像的压缩感知实验中，SSIM-BPFA算法所得字典也体现出了同样的优越性。

图4 Barbara重构结果及峰值信噪比

为了进一步验证不同投影观测数目条件下SSIM-BPFA所得字典的压缩感知性能，图5给出了观测数目分别为8、10、12、14、16、18等共6种条件下，在SSIM-BPFA算法、dHBP算法、DP-BPFA算法、BPFA算法和OMP算法所得字典表示下分别通过OMP算法对Barbara的重构相对误差，数据为50次实验结果的平均值。

从图5可以看出，随着观测数目的增加，不同算法字典下的重构相对误差均呈下降趋势，但总体重构相对误差由低到高分别是 SSIM-BPFA算法、dHBP算法、DP-BPFA算法、BPFA算法和MOD算法所得字典，其中，前四种算法重构相对误差均显著低于 MOD算法字典的重构相对误差，且SSIM-BPFA字典的重构相对误差显著低于其他字典的重构相对误差，这从另一个侧面表明SSIM-BPFA算法学习所得字典在压缩感知中的应用性能优于其他几种算法所得字典。其原因在于SSIM-BPFA算法基于全局结构相似性对图像进行了聚类处理，并引入了稀疏表示的块结构特性，使得字典对图像结构特征的表示性能得以改善，图像表示的稀疏度更小，从而提高了低观测数目条件下的重构成功率。尽管Gibbs采样推断方法的理论收敛性不易证明，但关于该推断方法收敛效果的可靠性和有效性均已在前人研究成果[9-12]中得到了实验验证。

5 结束语

本文提出一种基于结构相似性的非参数贝叶斯字典学习算法，将马尔可夫随机场思想引入到图像稀疏表示的块结构建模中，使字典具备了传统结构字典稀疏表示的块结构特性。实验表明，该算法所得字典的去噪性能和压缩感知性能优于BPFA算法、DP-BPFA算法和dHBP算法这3种非参数贝叶斯算法字典。本文以后将在两方面进行下一步研究：1）Gibbs采样推断计算量相对较大，这是BPFA算法同样面临的问题，且采样推断收敛性能的可靠性和有效性不易于理论证明，后续将研究效率更高的推断算法，并着重加强理论证明；2）图像结构相似性聚类过程采用K-means算法执行，虽简单易行复杂度低，但需要进行聚类数目的验证性优化，限制了算法的自适应性和顽健性，后续应着重提升无监督聚类的自适应性，以期在可观的复杂度之外，进一步改善字典的应用性能。