轮内电动汽车直接横摆力矩控制

严 友，李 美

(1.衢州职业技术学院，衢州 324000；2.海南大学，海口 570228)

0 引 言

随着汽车工业的发展，车辆已经成为社会生活中不可或缺的一部分[1]。然而，汽车的使用激增带来了一系列问题，如环境污染、交通安全、能源危机等，这些问题促使人们开始使用清洁能源汽车。电动汽车(以下简称EV)作为一种清洁能源汽车近来蓬勃发展起来。尽管EV有效地解决了环境污染和能源危机，但其安全性始终是人们关心的问题。不可否认的是，当EV在路面低系数、且速度较快时，更容易出现“侧滑”、“轻弹”、“急转弯”等现象，造成潜在的交通事故。

为了避免潜在交通事故的发生，越来越多的研究人员致力于车辆稳定性控制的研究[2]。目前，车辆稳定控制方法主要有直接横摆力矩控制(以下简称DYC)，防抱死制动系统(以下简称ABS)和牵引力控制系统(以下简称TCS)[3]。应该指出的是，DYC在稳定车辆运动方面比ABS和TCS发挥更重要的作用，因此它已被广泛用于车辆。DYC通过收集方向盘角度信息，判断驾驶员的意图，调整车辆偏航运动。附加的横摆力矩通过在内外轮之间施加不同的车轮力(驱动力或制动力)而获得，这通过电子差速器实现。但是，电子差分是昂贵且复杂的。作为EV的新形式轮内电动汽车(以下简称IEV)具有实现DYC的固有优势。它由4个/2个轮毂电机驱动，每个电机都可以独立控制一个车轮。因此，DYC能够方便简洁地在IEV上实现。

传统滑模控制算法[4-6]在DYC方面有着广泛的应用，但无法应对参数变化及不确定性干扰等情况。因此，针对上述问题，本文提出将传统的滑模控制与自适应鲁棒控制[7]相结合，充分发挥各自的优势，形成一种新方法，实现在外界干扰下具有良好的车辆操纵稳定性能。

1 系统模型搭建

1.1 整车二自由度模型

为了实现DYC在IEV稳定性方面的作用，首先建立了整车二自由度模型，如图1所示，该模型仅包括车辆横向和横摆2个自由度的运动。具体二自由度模型的表达式[8]如式(1)所示。

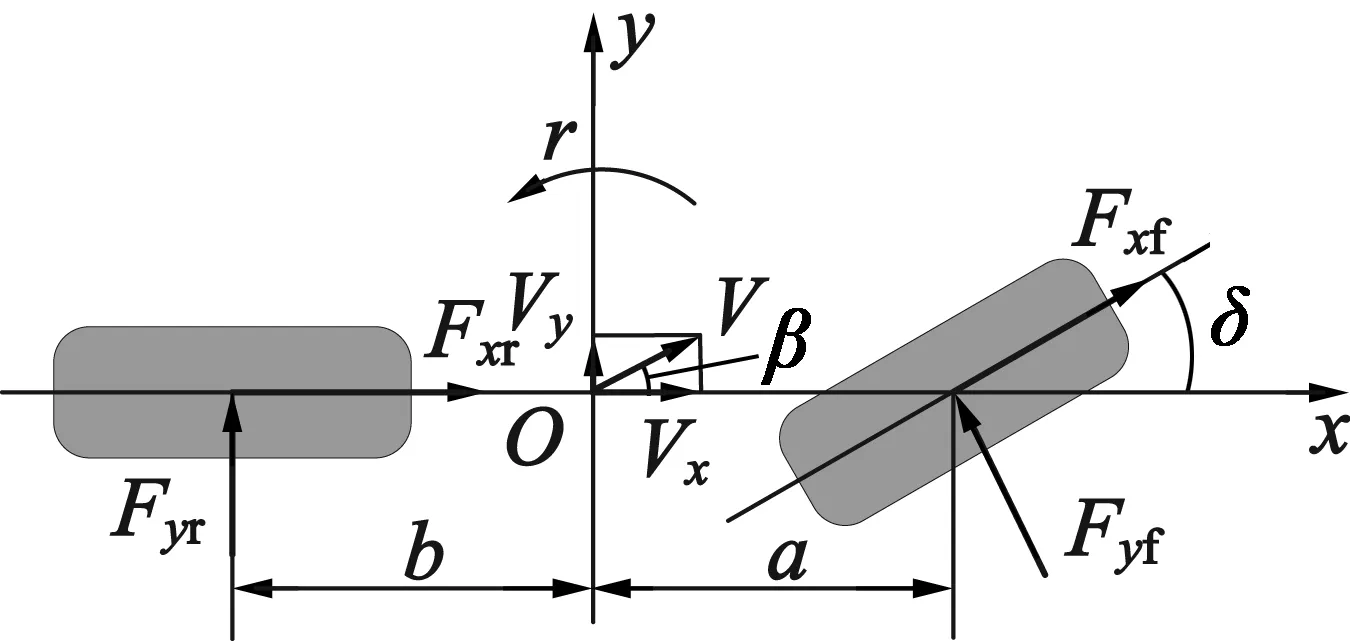
图1 整车二自由度模型

(1)

式中：m是车辆的总质量；Cf和Cr分别是前轮和后轮的侧偏刚度；β是质心侧偏角；r是横摆角速度；a和b分别是距离车辆质心的距离；δ是前轮转角；Jz是整车绕轴的转动惯量。Vx和Vy是车辆质心的纵向和横向速度，V代表车辆质心处的总速度。另外，图1中Fxi和Fyi分别表示纵向和横向轮胎力，而i表示前轮和后轮。

1.2 驱动电动机模型

本文对真实电动机模型进行了一些合理化假设[9]：忽略齿槽、饱和磁路、磁滞和温度变化的影响；定子绕组为60°相全绕组，三相定子绕组相互对称。其等效电路如图2所示，Ua，Ub，Uc分别为三相电压；ia，ib，ic为三相定子电流；ea，eb，ec为三相反电动势；R为电阻，Lm为互感差，具体等效电路如图2所示。

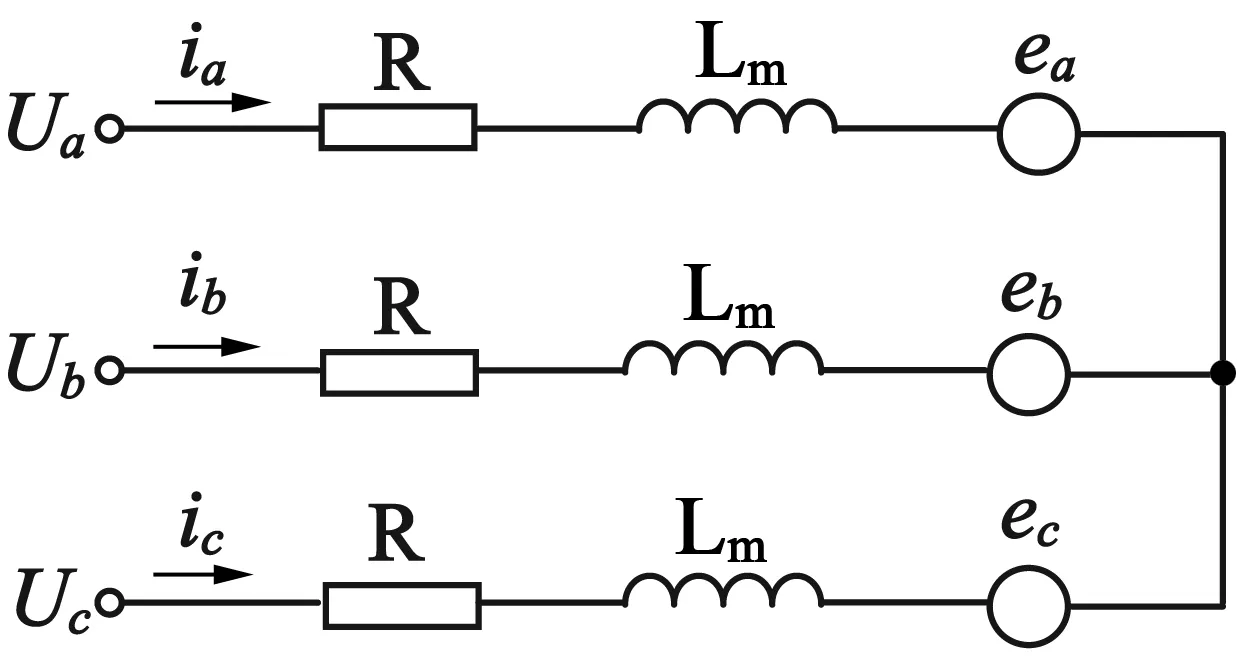
图2 电机等效电路

三相电压平衡公式[10]如下：

由于动态换相过程影响因素较小，可以忽略不计，永磁无刷直流电动机正常工作时，只有任意两相导通，另外一相关断。假设a，b两相导通，c相关断，则有ia=-ib=I，ic=0，ea=-eb=e，则式(2)可以转变为下式：

(3)

ea=keωm

(4)

式中：ke为电机转动系数；ωm为电动机转动速度。

电动机输出转矩：

(5)

式中：p为极对数；kT为转矩系数。

电机加载固定负载之后的动力学方程：

(6)

式中：Jm为电机的转动惯量；TL为加载到电机输出端的转矩。

令：U=Ua-Ub，联立式(3)～式(6)可得到：

(7)

式(7)即为建立的驱动电动机的动力学模型。

2 自适应鲁棒滑模控制律设计

在滑模控制过程中，始终要保持系统的状态在切换面上，所设计的控制策略也是为了保证其状态变量一直在切换面附近。本文设计的控制变量为横摆角速度r，建立其状态方程：

(8)

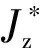
将状态方程改写成以下形式：

(9)

(10)

并有以下假设：

(11)

2) 不确定项Δ有界，表示：

|Δ|≤D

(12)

结合上面的推导，现开始自适应鲁棒滑模控制律的设计。

定义滑模函数：

s=ce

(13)

式中：e=r-rd为实际横摆角速度与理想横摆角速度之间的误差；c>0。则：

(14)

控制律设计：

u=ua+us1+us2

(15)

控制律中各项分别表示：

(16)

us1=-kss

(17)

us2=-ηsgn(s)

(18)

式中：ua为自适应补偿项；us1为反馈项；us2为鲁棒项；ks>0，η>D。故控制律可写为：

(19)

定义Lyapunov函数：

(20)

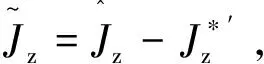
(21)

取自适应律：

(22)

则：

因此，系统是渐近稳定的，可渐近跟踪期望状态。

(24)

式中：Proj(·)表示限制因数，其表达式如下：

(25)

3 仿真验证

为了验证上述控制算法的有效性，搭建了如图3所示的DYC系统，该系统主要包括：车辆二自由度模型、自适应鲁棒滑模控制器和Carsim软件中车辆动力学模型3部分。其中，车辆二自由度模型的作用是用来实时计算理想横摆角度的参考值；自适应鲁棒滑模控制器的输入量是实际横摆角速度与理想横摆角速度之间的误差，其输出量为横摆力矩；Carsim软件中车辆动力学模型已对其进行了部分修改处理，即将软件中发动机模块与传动系统模块断开，并将本文建立的驱动电动机模型与软件中的传动系统相连，构建IEV的仿真模型。车辆具体仿真参数如表1所示。

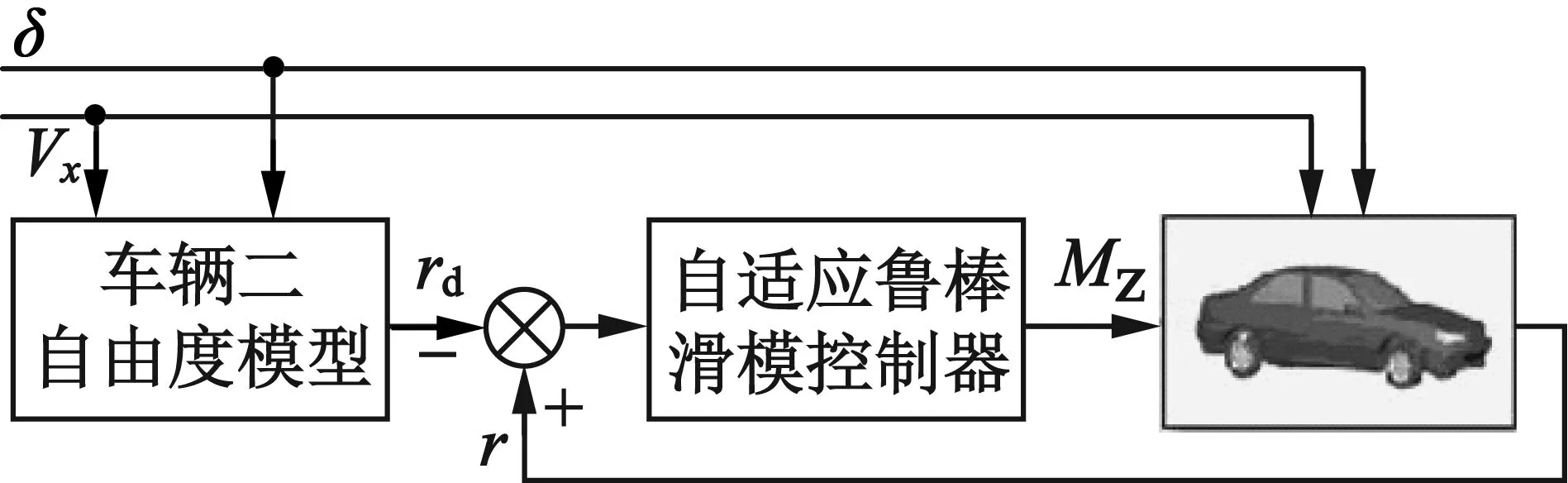
图3 DYC系统控制原理框图

表1 车辆仿真参数

具体设计的仿真工况如下：

(1) 无侧向风的情况下，进行双移线工况试验，试验车速为60 km/h，路面附着系数μ=0.8；

(2) 有侧向风的情况下，进行双移线工况试验，试验车速为60 km/h，路面附着系数μ=0.8。

在上述两种工况下，对横摆角速度和横摆力矩进行了对比分析，仿真结果如图4、图5所示。

从图4(a)可以看出，在无侧向风干扰的情况下，本文的控制方法可以较好地跟踪理想横摆角速度，使车辆在双移线工况中始终保持良好的行驶稳定性，控制效果明显好于无控制的情况，较好地抑止了无控制时在双移线工况下快速转向阶段出现了的较大横摆角速度偏差。横摆力矩变化情况如图4(b)所示。

从图5(a)可以看出，在有侧向风干扰的情况下，本文的控制方法虽然相比于无侧向风的情况，出现了较大的横摆角速度偏差，但是仍然可以较好地跟踪理想横摆角速度，且控制效果明显好于无控制的情况。从图5(b)也可以看出，在有侧向风的情况下，本文提出算法输出的横摆力矩的变化情况。

(a) 横摆角速度

(b) 横摆力矩

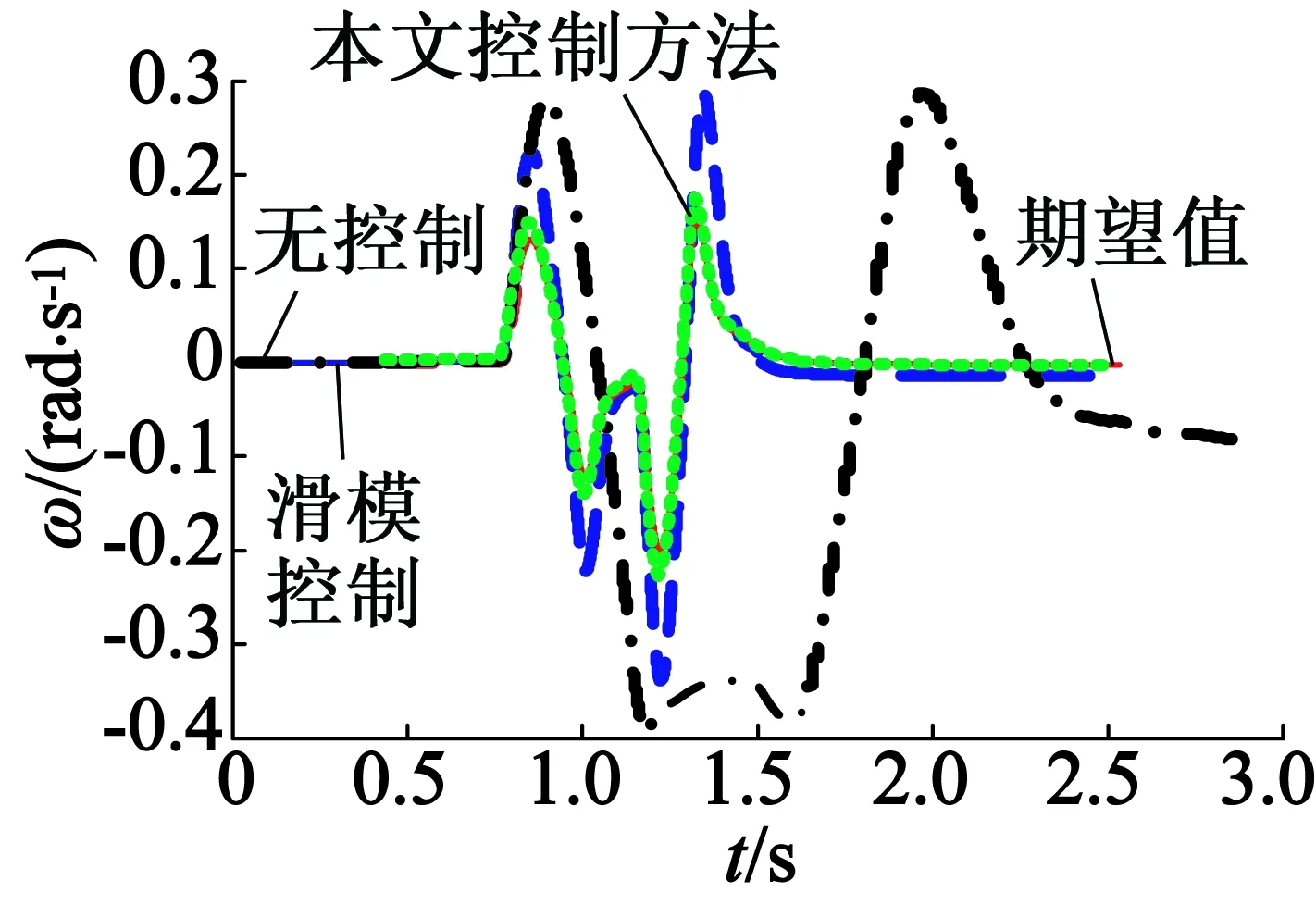
(a) 横摆角速度

(b) 横摆力矩

4 试验验证

为了进一步验证仿真结果的真实性，本文设计了相关试验对其结果进行试验验证。针对经典车型桑塔纳2000进行动力传动系统改造，轮毂电机作为主要驱动方式，同时要求前后轴两侧的轮毂电机具备电子差速功能，以满足转向工况的需求，试验车辆如图6所示，局部改装的现场图如图7所示。本文试验选取的轮毂电机的最大功率为8 kW，额定功率为4.5 kW，最大转矩为320 N·m，额定转矩为100 N·m，最大转速为 800 r/min。

图6 改制的试验车辆

图7 安装轮毂电机现场图

本文试验考虑安全因素的限制，主要进行了30 km/h的高附着系数路面的双移线试验，给出了实车试验以及仿真对比的情况，如图8所示。从横摆角速度的变化情况可以看出，虽然由于驾驶员的人为操作原因，导致方向盘转角的试验数据与仿真结果存在一定的偏差，但整体的一致性较好，横摆角速度由于传感器精度有限，试验数据存在一定的干扰信号，但从整体趋势上看，基本与仿真结果保持一致。因此，实车试验基本验证了本文所提出的直接横摆力矩控制策略的有效性。

图8 横摆角速度变化

5 结 语

本文建立了整车二自由度模型和电动机模型，并在Carsim软件中，构建以电动机为驱动方式的IEV，为后续的控制算法的设计打下模型基础。

设计了自适应鲁棒滑模控制律，构建基于上述控制算法的DYC系统，利用先进车辆动力学仿真软件Carsim对本文的控制策略进行了仿真实验。结果表明，该算法可有效实现直接横摆力矩控制，使车辆在有较大侧向风的干扰下保持行驶稳定性。

为了进一步验证仿真结果的真实性，针对经典车型桑塔纳2000进行动力传动系统改造，将轮毂电机作为其主要驱动方式。实车试验结果表明，本文的直接横摆力矩控制策略与仿真保持一致，验证了其算法的有效性。