高超声速双椭球气动热环境预测

朱志斌，尚 庆，潘宏禄，姜宝森

(中国航天空气动力技术研究院， 北京 100074)

高超声速飞行器表面气动热环境的准确预测一直是高超声速流动数值模拟的重点和难点。尤其是超声速飞行器存在的激波/边界层干扰会在局部区域产生严重的气动热载荷，对飞行器防热系统设计带来严峻的考验。高超声速气动热是由流体粘性起主导作用的物理现象，在计算中受网格分布、数值格式、边界条件算等因素的影响，其交错影响决定了热流计算的复杂性[1]。因此，合理有效的数值方法对于高超声速飞行器热环境的准确预测具有重要意义，进而能够为飞行器热防护系统的低冗余度设计提供有力支持。

双椭球模型是典型的高超声速飞行器外形，具有飞机机身与座舱组合的特征，其超声速绕流流场中存在三维弓形头激波、二次激波以及三维分离流动。国内外对此外形开展了大量的风洞试验研究[2-6]，测量数据包括压力、热流密度、纹影照片、表面油流显示等，这些结果相互补充，用来描述其复杂流场特征。李素循[5]针对该外形，选择四座中等尺度的高超声速风洞，分别开展了测力与测热实验，提供了详细的测点数据，为验证计算流体力学数值模拟方法提供了依据。

高超声速双椭球绕流流场中包含激波与边界层的干扰、旋涡、分离和再附运动，具有复杂的干扰特征，精确预测其流动结构及其气动热环境存在较大难度。国内外已有文献采用不同数值方法对该问题进行了模拟分析。Riedelbauch等[7]采用半隐式有限差分方法对高超声速双椭球绕流流场进行了层流模拟，捕捉到了激波/激波干扰、激波边界层干扰以及流动分离等现象，与实验图像一致。刘昕等[8]通过层流计算，对比了不同格式对双椭球热流分布的影响，认为高阶格式得到的热流密度更准确可靠。耿云飞等[9]对比评估了不同湍流模型对与高超声速双椭球绕流的适用性，发现考虑可压缩性修正得到的壁面热流更准确。贺立新等[10]将DG方法应用于双椭球高超声速粘性绕流计算，得到的热流曲线与实验数据分布规律一致。以上数值模拟研究均捕捉到了基本流场结构特征，侧重于对比验证数值格式、湍流模型、离散方法等因素对双椭球热流分布计算结果的影响，而很少关注真实物理现象，并且没有针对性地考虑流动分离诱导的转捩现象对气动热环境的影响。

本文针对高超声速双椭球模型，采用层流、转捩、全湍流不同数值模拟方法进行流场气动热环境模拟，通过与风洞试验数据对比，分析计算网格、计算格式和湍流模型等气动热环境预测的影响；并采用大涡模拟，进一步对激波边界层干扰诱导以及流动分离、转捩、再附等物理现象进行更细致地模拟计算，分析认识高超声速双椭球模型的复杂流场结构，从而为该类外形高超声速气动热环境的数值模拟预测提供借鉴和参考。

1 计算模型及来流条件

计算模型及来流条件与文献[5]中FD-14A激波风洞的测热试验一致。双椭球模型几何外形如图1所示。

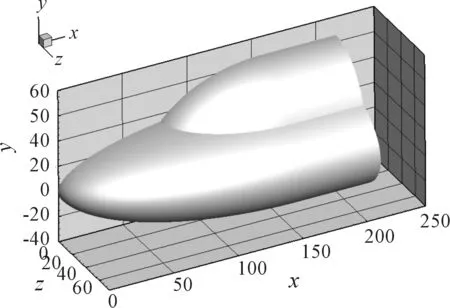
图1 双椭球模型示意图

模型几何外形表面方程用以下公式描述(单位mm):

风洞试验试验段马赫数Ma=8.04，迎角0°，来流条件如表1所示。

表1 试验来流条件

以标准球头(R=15 mm)模型零攻角下的驻点热流密度值作为热流参考值Qref=568.4 kW/m2。实验数据包括上下表面中心线测点，以及距模型前端距离78 mm和120 mm的两个剖面。

2 数值方法

1) 层流计算方法

层流计算不考虑转捩和湍流影响，直接求解守恒形式的三维可压缩Navier-Stokes方程，对流通量离散格式分别采用Roe格式[11]以及前期发展的满足几何守恒律的WENO格式[12]。Roe格式是典型的线性化Riemann解，不仅具有很好的激波等间断分辨率，同时具有较高的粘性分辨率。满足几何守恒律的WENO格式采用守恒型网格导数计算方法，将标准的WENO格式分解为中心差分部分和数值耗散部分，能够消除网格导数计算误差，保证来流保持性，并具有较高的精度和分辨率。

粘性项离散选取二阶中心差分逼近粘性二阶导数平方项和交叉项。时间推进采用LU-SGS隐式方法。

2) 雷诺平均方法

RANS(Reynolds Averaged Navier-Stokes)方法求解雷诺平均N-S方程，可获得湍流流动的时间平均信息，并给出工程问题关心的平均流场、雷诺应力和基本气动力热等信息，是工程中使用最为广泛的湍流流动计算方法。RANS方法需要引入湍流模型来封闭方程，常用的湍流模型有一方程SA模型[13]以及两方程SST模型[14]。SA模型从经验与量纲出发，只需求解一个涡粘性系数满足的输运方程，其构造简单、鲁棒性好，并且对壁面网格质量依赖小。SST模型是k-ε模型与k-ω模型的混合模型，由于该模型不需要显式的壁面衰减函数，因而适用性好。

3) 转捩模式方法

为模拟流动转捩现象，采用基于SSTk-ω模型的γ-Reθ转捩模式[15]，该模型把经验关联方法和间歇因子方法有机地结合了起来，最终目的是求解间歇函数γ(即空间某点的流态是湍流的概率)，并通过它与湍流模型的联合来控制转捩的发生。该模型不仅建立了间歇因子的方程，而且建立了动量厚度雷诺数的方程，并且利用已有的一些试验数据构建了它们彼此之间的关联还能够反映来流湍流度的影响，已在高超声速钝双楔绕流流动中进行了验证[16]。

4) 大涡模拟方法

大涡模拟(Large Eddy Simulation，LES)求解空间Favre滤波形式的三维非定常可压缩Navier-Stokes方程，对大尺度运动通过求解运动微分方程直接计算，小尺度运动对大尺度运动的影响通过亚格子应力来模拟。本文采用隐式大涡模拟方法[17,18]，以数值格式耗散代替亚格子模型作用。大涡模拟方法要求采用高精度高分辨率的计算格式，以精细分辨流场小尺度结构。本文采用特征通量限制型紧致格式[19]，在光滑捕捉流场间断的同时，精细刻画小尺度流场结构。时间推进采用二阶显式Runger-Kutta方法。

5) 计算网格及边界条件

本文不考虑侧滑角影响，针对半模模型进行计算，壁面采用无滑移等温条件，壁面温度设为300 K。

采用贴体结构网格对计算域进行空间离散，在相贯线附近以及近壁区域均进行了适当的加密，基准网格物面法向间距为0.002 6 mm，对应网格雷诺数为对应网格雷诺数为30，网格单元总量1 998 000。为分析计算网格的影响，在基准网格基础上，一方面，对物面法向网格进行进一步加密，第一层网格尺度设为0.001 mm，对应网格雷诺数为11；另一方面，采用拼接网格对分离区影响区域进行加密，拼接网格单元总量7 626 000。计算网格如图2所示。

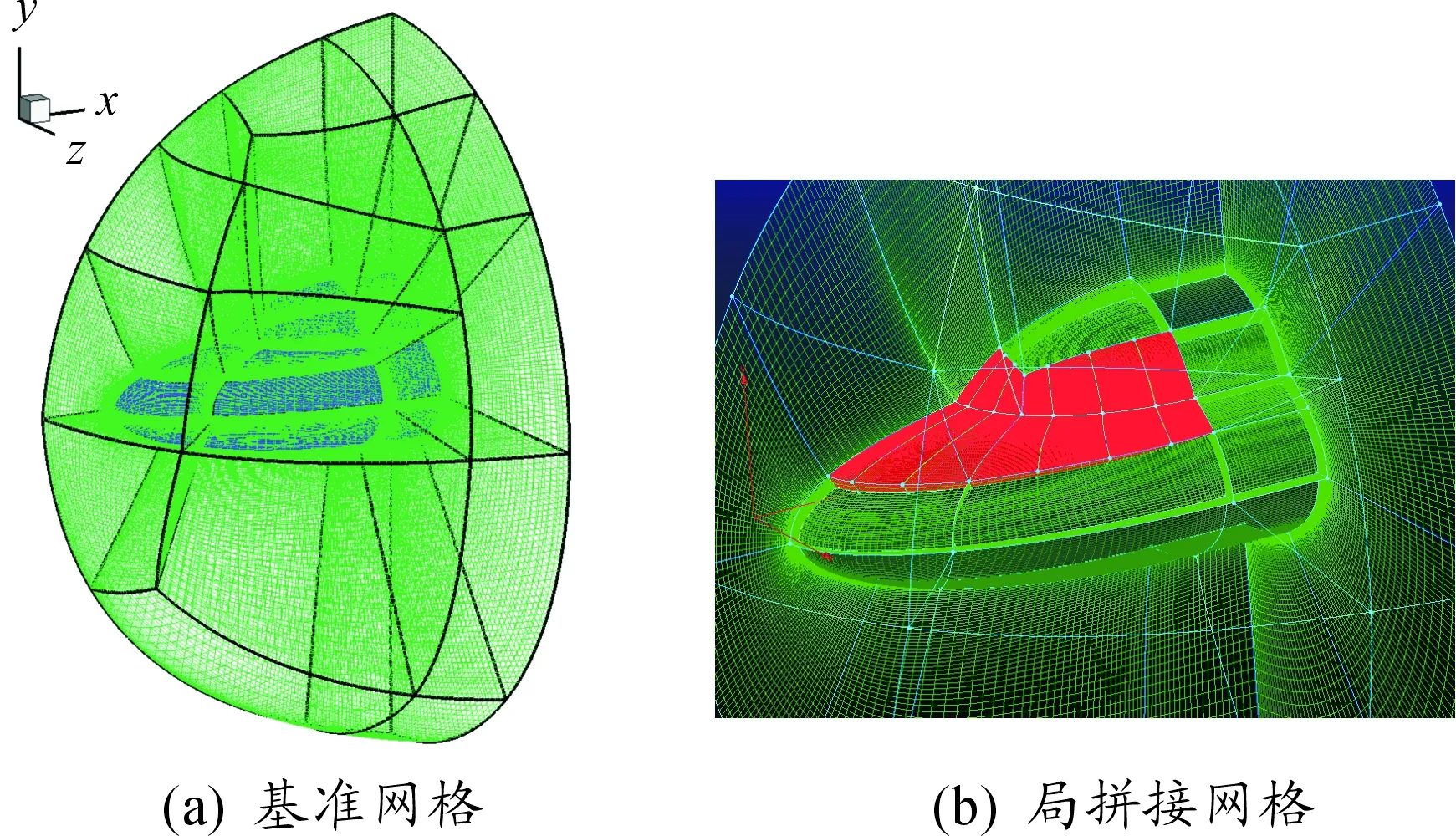
图2 计算网格示意图

大涡模拟计算中采用拼接网格在流动分离影响区域进行加密，以解析流动分离诱发转捩等复杂流动现象，计算网格如图3所示。网格单元总量 84 240 000，其中加密区域网格量为83 016 000。

3 结果分析

3.1 层流计算对比

首先通过层流计算，对比分析计算网格、数值格式对双椭球外形高超声速气动热环境计算结果影响。

1) 计算网格影响

在基准网格下采用Roe格式计算得到的流场如图4所示，可以看到，高超声速来流在下椭球头部产生弓形激波，并与上椭球激波发生干涉，两椭球相贯线附近出现三维流动分离。

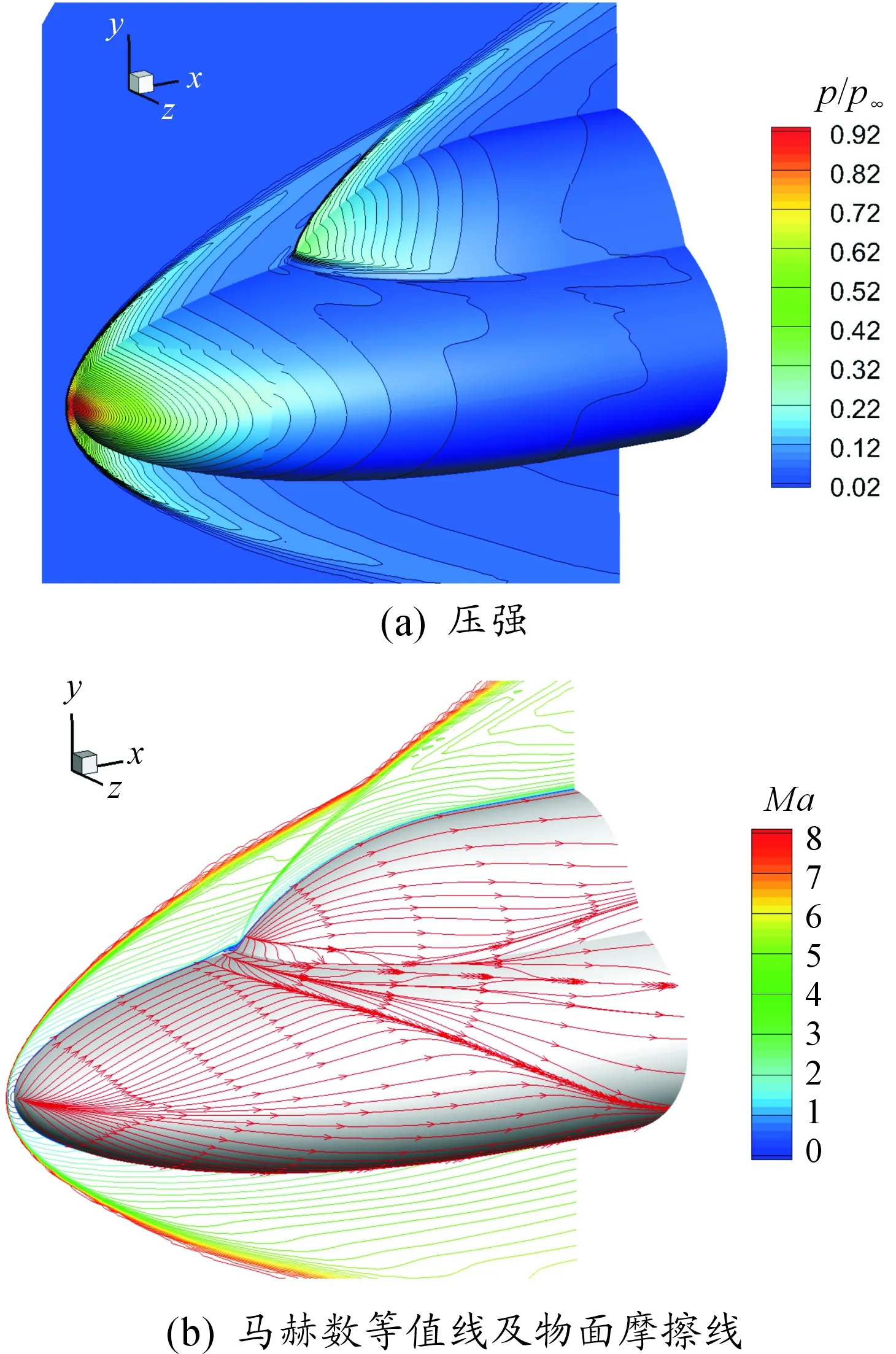
图4 高超声速双椭球绕流流场

采用不同网格得到的对称面物面热流同实验数据对比如图5所示，基准网格和加密网格得到的热流值几乎重合，表明基准网格雷诺数已达到计算要求；而采用拼接网格得到的计算在相贯线附近热流曲线出现振荡，这是由于拼接网格在分离区域空间网格尺度小，对小尺度流动结构分辨更为精细，捕捉到了流动非定常特性。

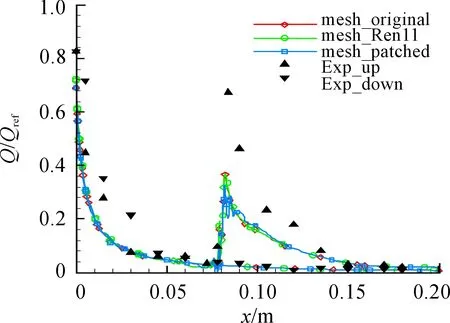
图5 不同计算网格对称面热流对比

从对称面回流区流线计算结果对比(图6)可以看到，基准网格和加密网格计算得到的分离涡形态一致，而采用拼接网格计算得到的涡结构更为复杂，在一定程度上分辨出了分离涡的发展演化形态。

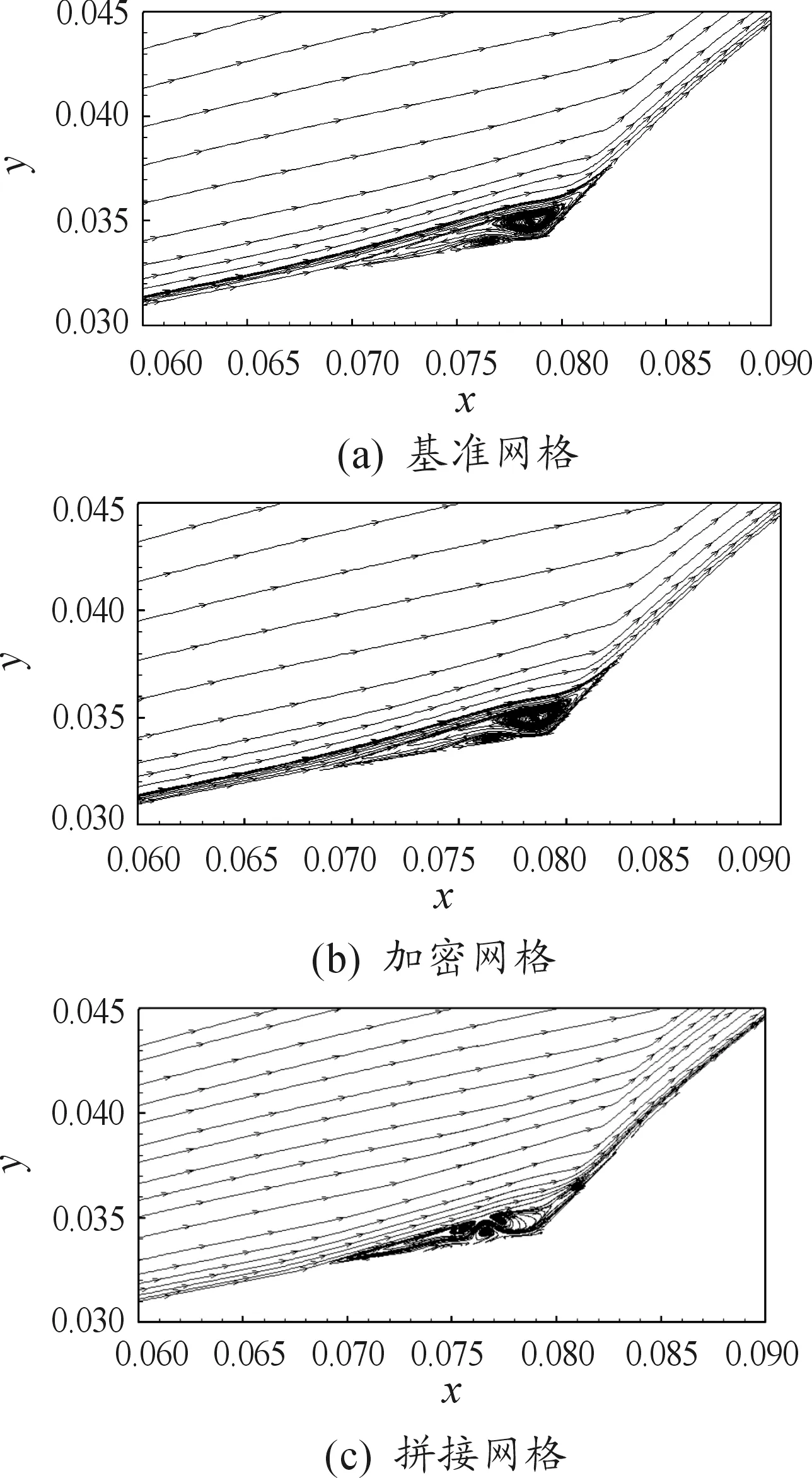
图6 不同网格对称面流线对比

2) 数值格式影响

分别采用Roe格式以及满足几何守恒律的WENO格式，采用基准网格进行层流计算，结果对比分析如下。

从对称面和流向位置处的热流曲线对比(图7)，可看到，不同精度WENO计算格式得到的热流值与Roe格式结果略有差别，热流分布规律一致，采用高阶格式得到的计算结果与实验数据误差并无明显改进。

图8给出了Roe格式与5阶WENO格式流场计算结果，对比可发现，不同数值格式均光滑捕捉到了下椭球头部弓形激波及其与上椭球激波的干扰，从壁面流线可以看出激波、边界层干扰引起的一次和二次分离。高阶格式对激波的捕捉更为精细。

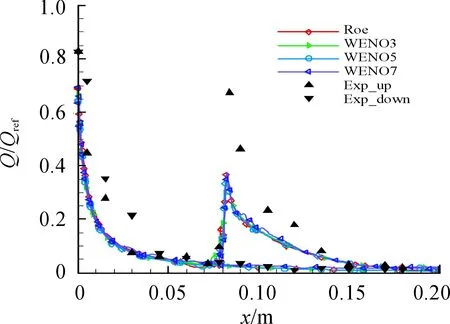
图7 不同格式对称面热流结果对比

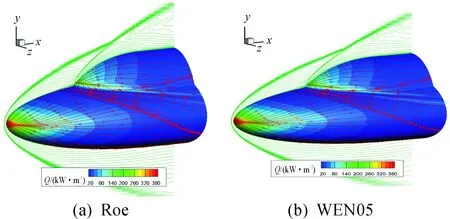
图8 不同格式等Ma线，壁面摩擦线及热流分布计算结果对比

从对称面回流区流线对比(图9)可以看出，高精度计算格式得到的回流区涡形态愈加复杂，涡由一个主涡和二次涡变为三个涡。这是由于高阶格式具有较高的精度和分辨率，对流动小尺度流动结构的分辨能力强，从而捕捉到了流动分离涡的运动演化。

图9 不同格式对称面流线对比

3.2 转捩模式及湍流模型计算

分别采用SA模型和SST模型进行全湍流计算，并采用转捩模式对分离诱导产生的转捩进行预测。

从对称面热流曲线对比(图10)可以看到，一方面，转捩模式和全湍流计算得到的热流峰值较层流明显提高，其中转捩模式与实验数据吻合最好，全湍流SST模型次之；另一方面，全湍流计算的下椭球热流值明显高于层流和转捩模式结果。

不同流向位置处热流分布对比如图11所示，从图11中可发现，在上表面(0°～90°)转捩模式计算结果介于层流和湍流之间，分布规律与实验数据一致，在下表面(90°～180°)转捩模式与层流热流计算结果重合。

图10 不同模型对称面热流结果对比

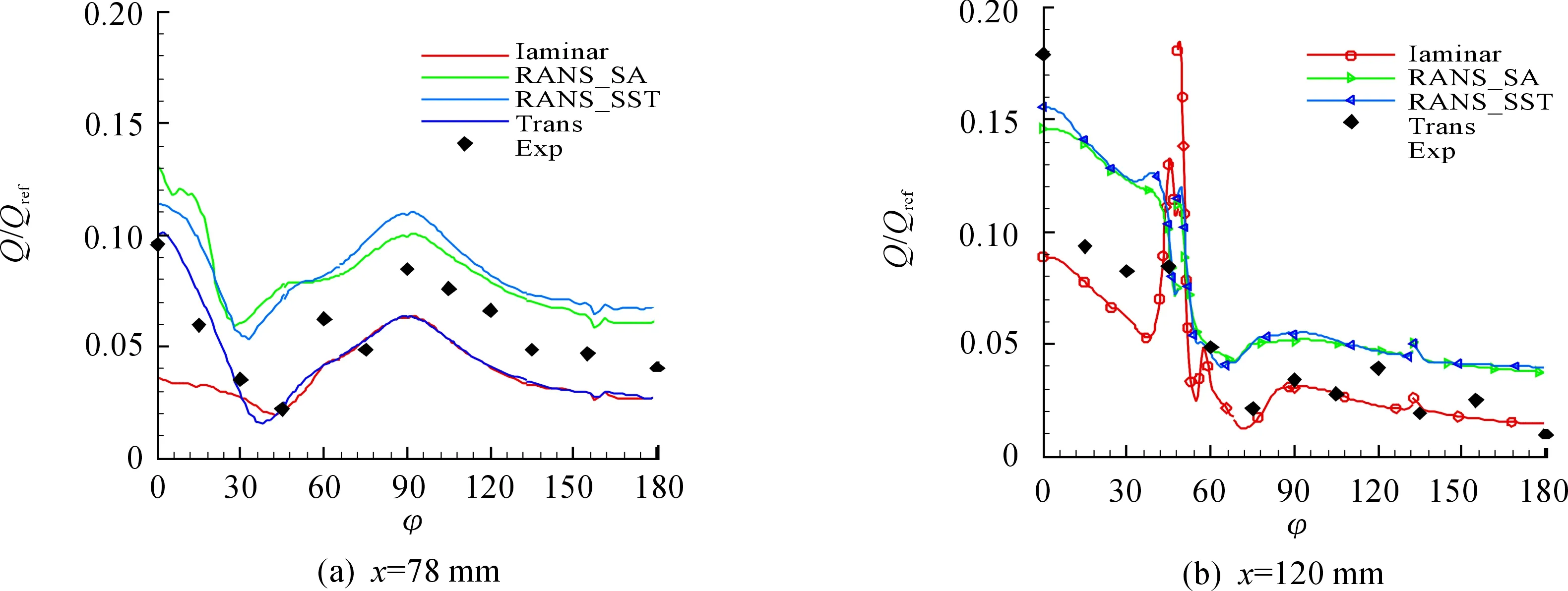
图11 不同模型流向位置处热流结果对比

图12为转捩模式计算得到的湍流区域示意图(以湍流与层流粘性系数之比的等值面表示)，可以看到，流动在下表面保持层流，上表面流动在分离影响区域发生转捩及湍流化；上椭球顶部附近由于顺压梯度，流动发生再层流化。而全湍流计算得到的湍流范围较广，得到的热流密度值偏高。 从表面极限流线(图13)和对称面流线(图14)对比可发现，层流计算结果流动在相贯线附近发生二次分离，而转捩模式和全湍流计算结果只得到一个主涡，其中转捩模式得到的涡的大小与层流接近，全湍流计算结果相对较小。

图12 湍流区域示意图

图13 不同模型极限流线计算结果

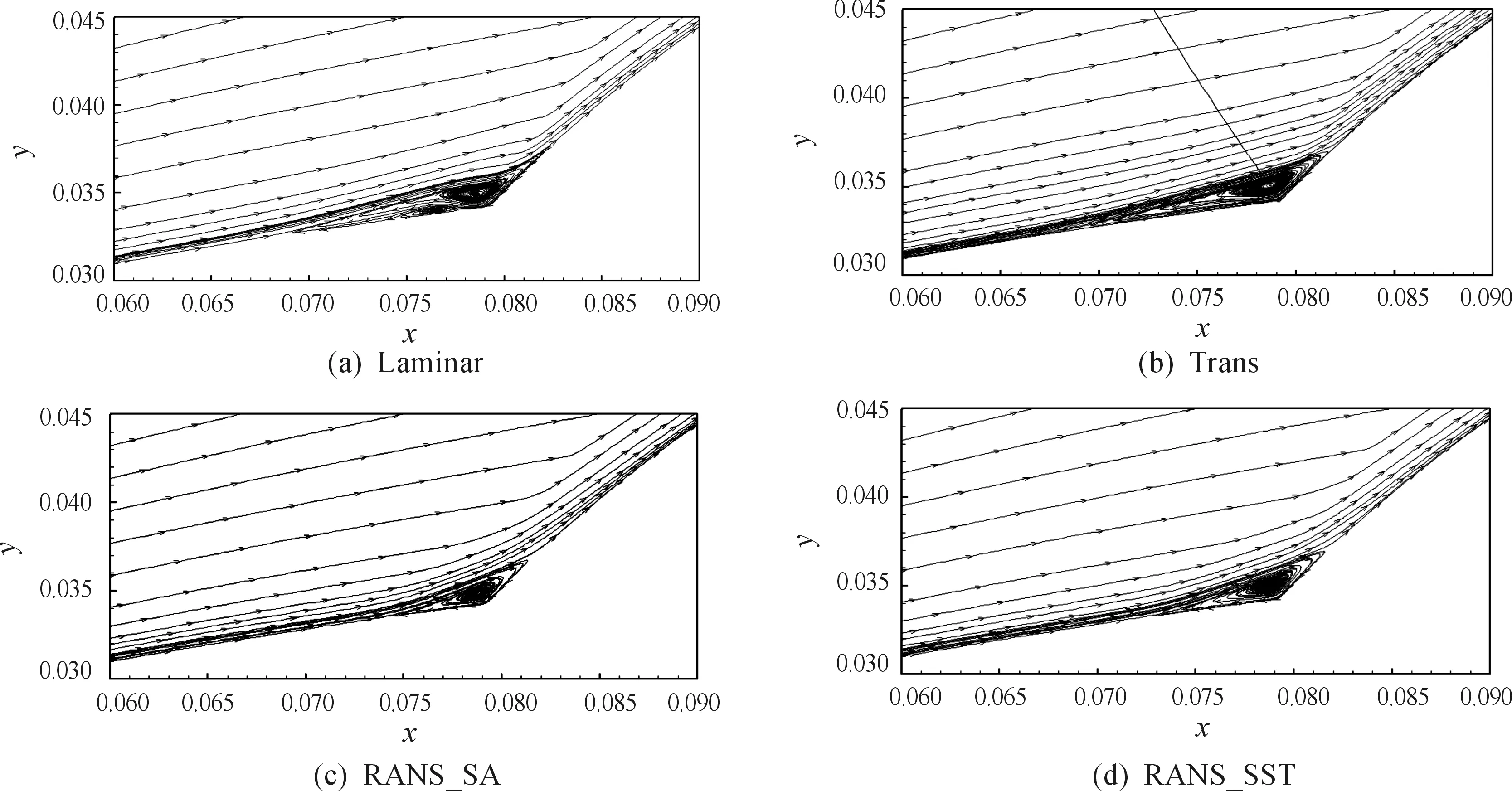
图14 不同模型对称面流线

3.3 大涡模拟分析

为进一步认识高超声速双椭球绕流流场结构特征及热流分布规律，采用大涡模拟方法进行模拟分析。

图15显示了流场瞬时涡系结构，从中可以看到，相贯线附近激波与边界层干扰引起流动分离，诱导产生的湍流相干结构沿流动方向进一步发展和演化。图16为统计平均热流分布，上椭球局部区域热流值较高；对比可发现，流场涡系结构与热流分布直接相关。

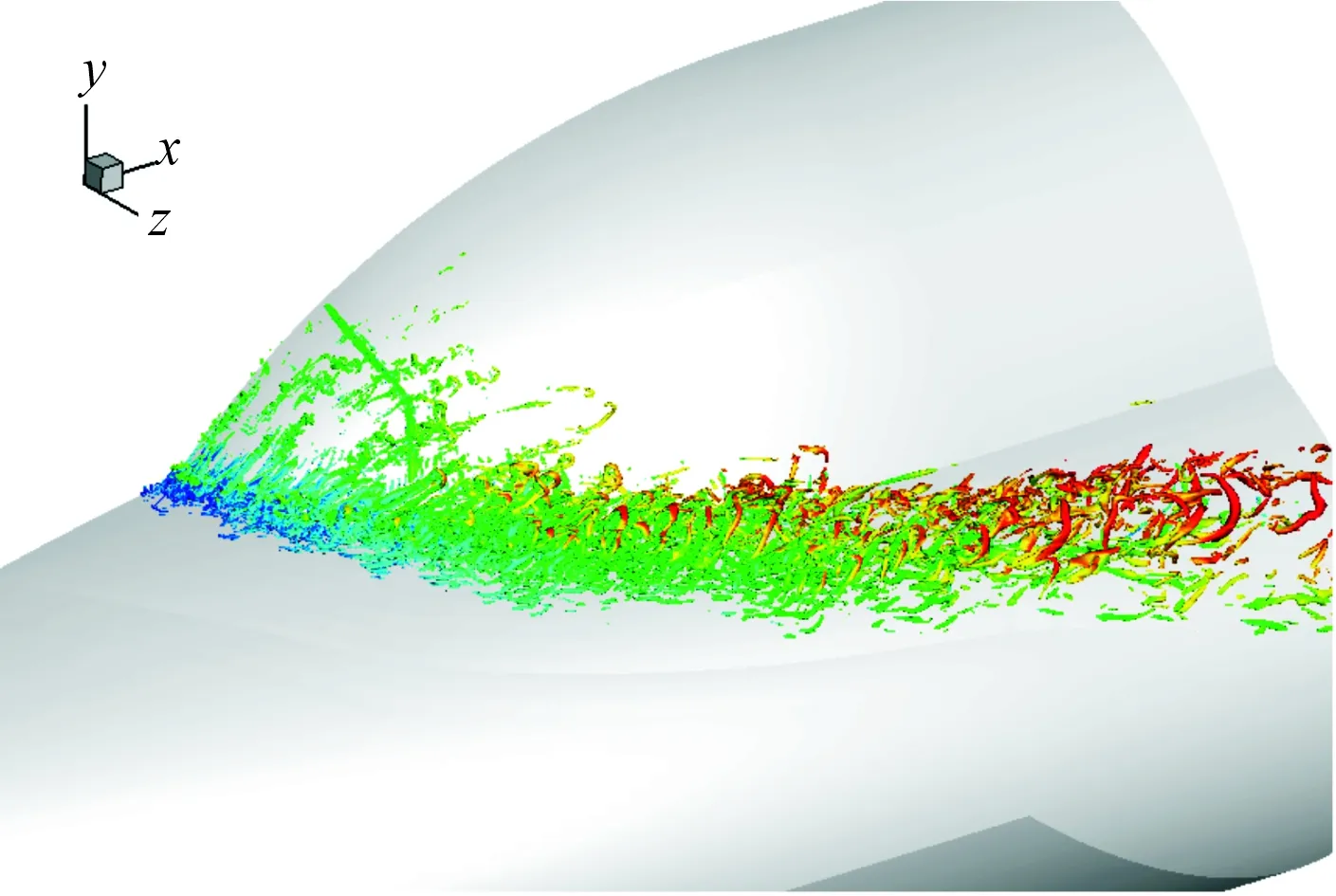
图15 瞬时涡系结构(Q准则，流向速度着色)

图16 平均热流分布

从热流分布曲线对比(图17和图18)可以看到，大涡模拟计算得到的热流曲线抖动明显，表明流场非定常特征导致局部区域的热流密度值不稳定，热流数值介于层流和全湍流结果之间，与实验数据出现偏差的原因可能在于来流雷诺数高，采用的计算网格未能充分解析小尺度边界层湍流结构。

图17 对称面热流曲线对比

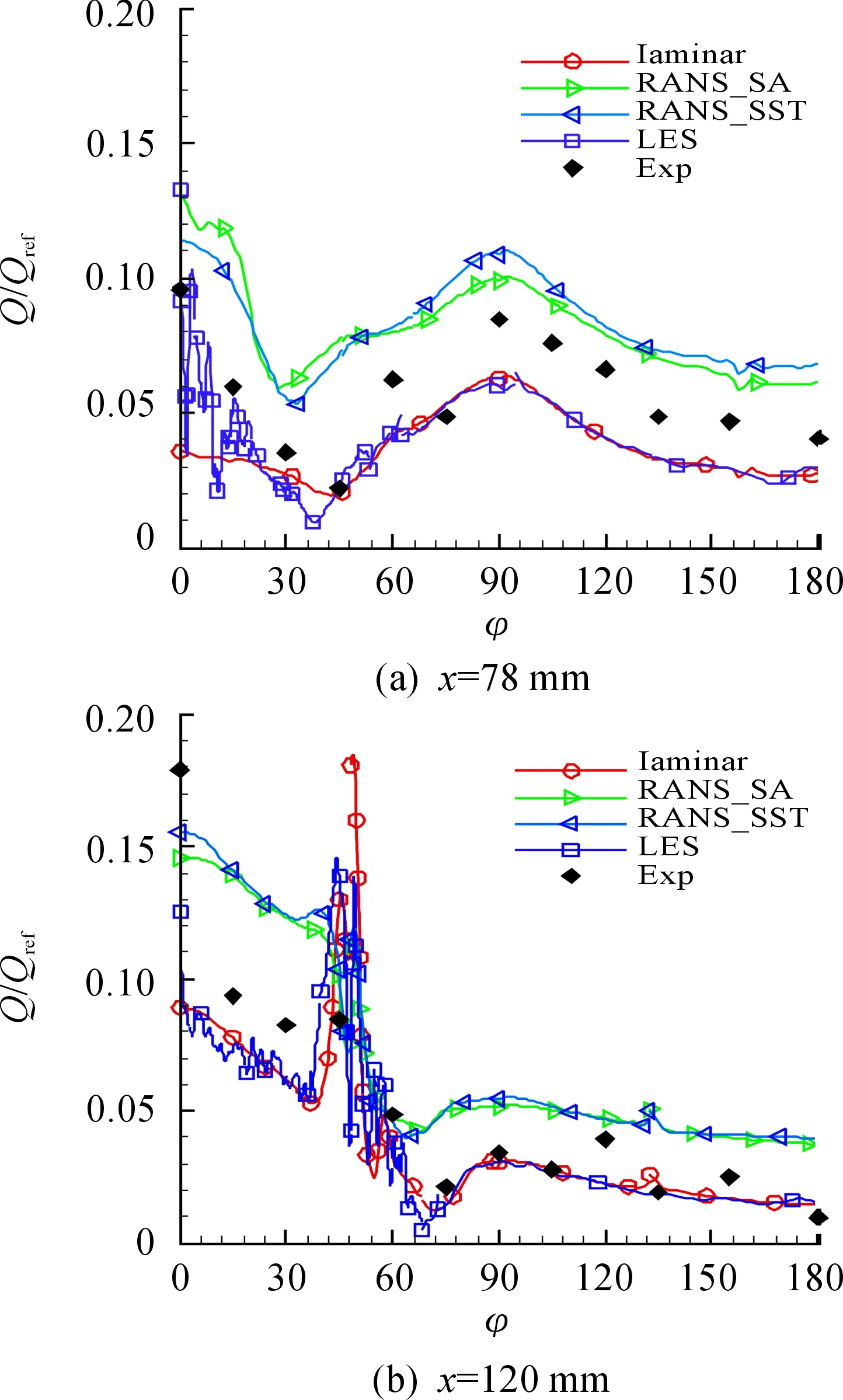
图18 不同流向位置处热流曲线对比

4 结论

1) 高超声速双椭球绕流流场中存在激波/边界层干扰、流动分离、再附等非定常流动现象，流动分离旋涡剪切作用会诱发流动转捩，从而改变边界层流动状态，并直接导致相贯线附近热流急剧升高。

2) 层流计算无法模拟流动转捩和湍流对气动加热影响，得到的热流密度值偏低；全湍流计算得到热流峰值与实验数据吻合较好，但高估了湍流影响范围；而采用关联转捩模型方法得到的计算结果与试验数据符合最好，对流动分离引起的转捩和湍流化现象的模拟更为准确。大涡模拟计算获得了三维分离涡发展演化并诱发边界层转捩的时空发展过程，有利于揭示流动演化及其热流分布的物理机理。

3) 基于转捩模式的流场计算方法，能够较为准确的模拟转捩位置、湍流区域等流动现象，从而得到正确合理的气动热环境，同时计算量较小，在高超声速飞行器气动热环境预测中具有广泛的应用前景。