基于模糊规则预测模型的急性高血糖诊断
2019-02-25冯宇
冯 宇
(长安大学 电子与控制工程学院,陕西 西安 710064)
0 引 言
近年来,国内人口高血糖的患病率呈现逐年上升的趋势[1-2]。急性高血糖可直接造成脑损伤[3],并影响心脏传导系统的功能[4],严重威胁着人类健康,目前亟需研究可以判断急性高血糖的方法。从算法分析角度来看,医学诊断过程的实质是分类与预测,因此预测模型在医学诊断领域中有广泛的应用前景。预测模型是数据挖掘研究领域中的重要组成部分,其功能是建立连续值函数模型,预测给定自变量对应的因变量的值[5]。预测的目标是建立一个预测函数,使得对于每一个提前期,实际值与预测值之间的偏差的均方尽可能小[6]。在多种建立预测模型的方法中,模糊分析方法因其分析对象的系统性、数学表达的简洁性和较少的数据信息需求,广泛应用于医学诊断研究领域[7-9]。文中建立了一种基于模糊语言规则(fuzzy language rules,FLR)的预测模型,通过该预测模型分析心脏传导系统的电生理信息,进而实现对不同浓度急性高血糖作用时间的判断。
1 关键技术
当系统中有不确定的信息时,可以认为系统是模糊的。模糊模型介于单纯的经验模型和严格的结构模型之间,实际中的大部分模型都具备这样的特点,且模糊的推理方式更接近于人类的思维和语言特点。经验表明,使用模糊算法生成的预测模型往往具有更高的预测精度。
1.1 模糊集合和模糊推理
若X是对象x的集合,则X的模糊集合A定义为:
A={(x,μA(x))|x∈X}
(1)
其中,μA(x)为模糊集合A的隶属函数。
隶属函数可以将集合X中的每一个元素在0到1的区间上重新映射,称为隶属度。隶属函数的值在区间0到1之间是连续变化的。
一般可以将模糊推理过程分为三步:
第一步,根据分类方式确定输入变量的隶属度,即数据模糊化。
第二步,将模糊化的输入变量输入模糊运算规则库,使用规则库中的多种运算规则得到系统的输出变量,该输出也是模糊化的。
第三步,对输出变量解模糊处理,最终得到确定的结果。
设计合理的算法,精确、高效地建立模糊规则库是实现上述三个步骤的前提,也是建立模糊预测模型的核心内容。
1.2 Takagi-Sugeno模型
Takagi-Sugeno模型(T-S模型)最早由Takagi和Sugeno提出[10],是把输入变量空间划分成若干个模糊的子空间,每个子空间的特征均可以使用线性或非线性模型描述,混合这些模型即可得到系统的总体模型。
T-S模型通过IF-THEN语句描述规则,每条规则对应一个子系统,规则前件表示模糊子空间,规则后件则是输入的线性或非线性组合。对于一个模糊系统,令Ri为第i条规则,则T-S模型可以表述为:
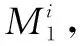
THENy(t)=Aix(t)+Biu(t),i=1,2,…,r
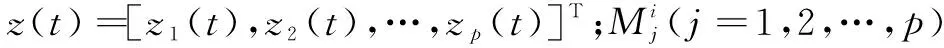
若在模糊推理过程中分别使用单点模糊化、乘积推理和加权平均去模糊化,则上述模型可以表示为:
(2)

令:
(3)
则:
(4)
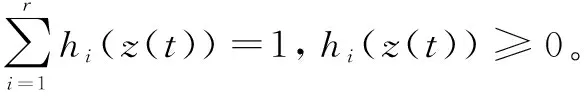
1.3 基于模糊规则的预测模型
文中使用的基于模糊语言规则的预测模型采用IF-THEN的表述方式来描述规则[11]。算法的输入矩阵用[x1,x2,…,xn]表示,模糊集用{L1,L2,…,Lm}表示,则一条规则可以表示为:
规则i:
IF
xp1∈Lq1andxp2∈Lq2… andxpn∈Lqn
THEN
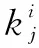

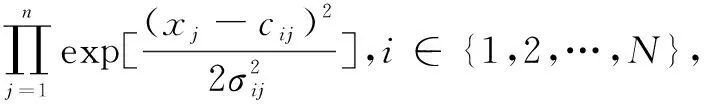
j∈{1,2,…,n}
(5)
其中,σij为标准差;cij为期望值。
这样,系数可通过式6计算:
(6)
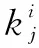
(7)
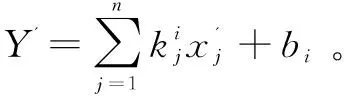
2 数据来源与实验设计
2.1 实验动物
实验使用雄性C57/BL6J小鼠,年龄为8~12周,体重20~25 g,小鼠使用标准的实验室饮食和水饲养,饲养环境温度为21±2℃,光照为有光条件和无光条件各12小时循环。实验操作过程符合长安大学生物实验操作规程和伦理学要求。
2.2 实验设备
实验使用MED64微电极阵列测量系统(AlphaMedScience,日本)来进行数据采集和分析。每个传感器包括64个电位记录点,在平面空间呈8×8方式排列,电极间距300 μm,每个电极为正方形,边长为50 μm。该传感器可以直接测量小鼠心脏表面的场电位分布。实验系统还包括信号放大器、连接器、控制器、处理数据的计算机、倒置显微镜、灌流槽和蠕动泵等。
2.3 实验设计与数据提取
取出小鼠心脏,使用有钙台式液和Langendorff离体心脏灌流方法[12]进行离体灌流。心脏传导系统的电信号由心脏窦房结发出,窦房结位于右心房,实验中将右心房置于下方,直接与传感器测量平面接触,之后进行信号测量。在整个测量过程中,给样本持续提供加入了5%二氧化碳和95%氧气的有钙台式液,流速为5 ml/min,每次实验中给样本加入不同浓度的高糖溶液,浓度间隔为10 mM。在每次实验中,首先记录对照样的测量信号,随后,从第0 min开始加入高糖溶液,持续加入30 min。每种浓度加入后,从第0 min开始,每间隔5 min测量一次,采样频率为20 kHz,每次测量持续30 s,每次可同时测量64个信号。随后,对实验数据进行预处理,提取出每次测量到电位信号的最大正振幅、最大负振幅、频率、单次信号持续时间等特征值。再将提取出的特征值作为预测模型的输入矩阵,高糖作用时间作为预测模型的输出,把实验数据分为训练集和验证集[13],训练集用于确定预测模型的系数,验证集用于检验预测结果。
3 实验结果与分析
图1给出了测量信号的相关特征值在不同浓度的高糖溶液作用下,持续30分钟后的变化率。其中,MPA为最大正振幅;MNA为最大负振幅;FRE为频率;SVD为单次信号持续时间。
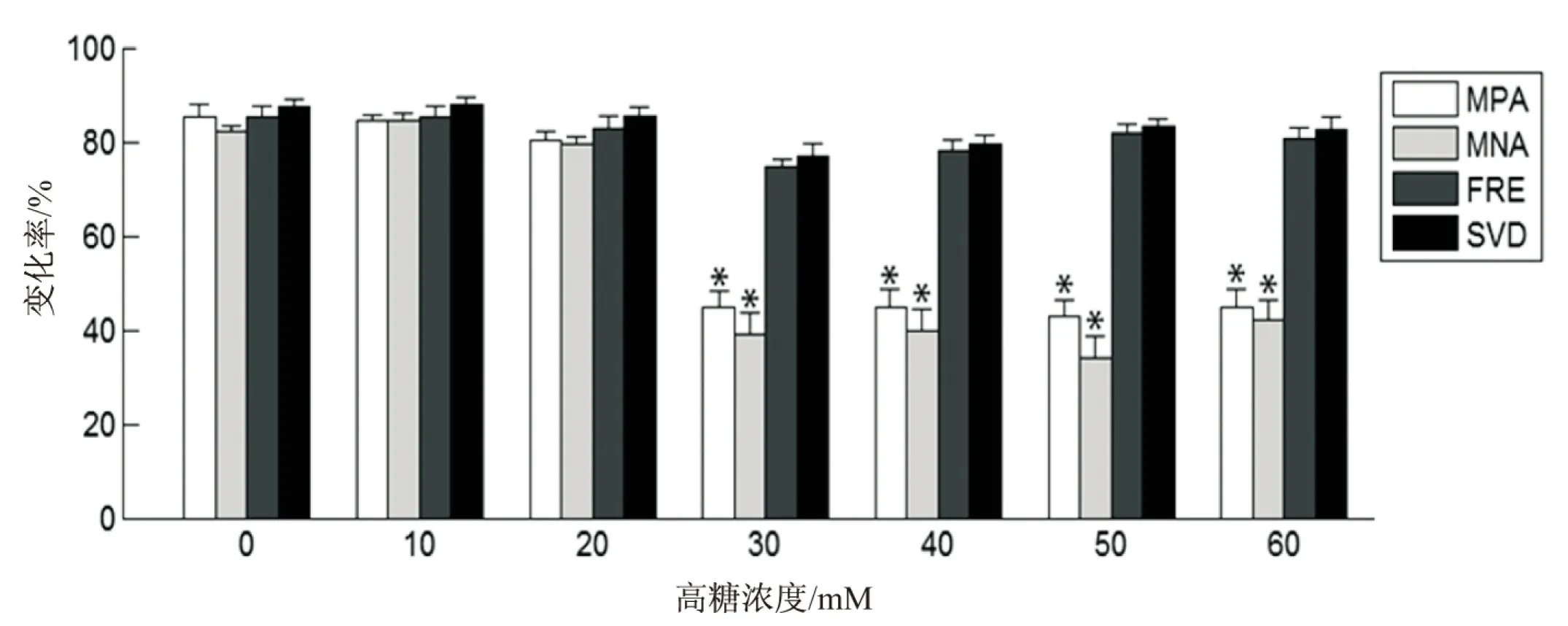
图1 不同浓度高糖溶液作用30 min后测量信号特征值的变化率(*P<0.05 vs. 0mM)
从图中可以明显看出,当高糖浓度高于30 mM时,测量信号变化明显,因此,后续实验中选用高糖溶液浓度分别为30 mM,40 mM和50 mM的环境进行预测建模与分析。经过数据预处理后测得有效的实验数据分别为1 264组、1 208组和1 221组,通过训练集生成基于模糊语言规则(FLR)的预测模型规则库,并使用验证集预测不同浓度下高糖溶液对心脏的作用时间,进而检验预测结果。同时,对于相同的验证集,使用三种经典的预测模型进行预测,并与文中使用的方法进行比较,三种经典的预测模型分别为偏最小二乘法(PLS)、最小二乘支持向量机(LSSVM)和反向传播神经网络(BPNN)[14-16]。表1~3分别给出了三种高糖浓度下的实验结果。
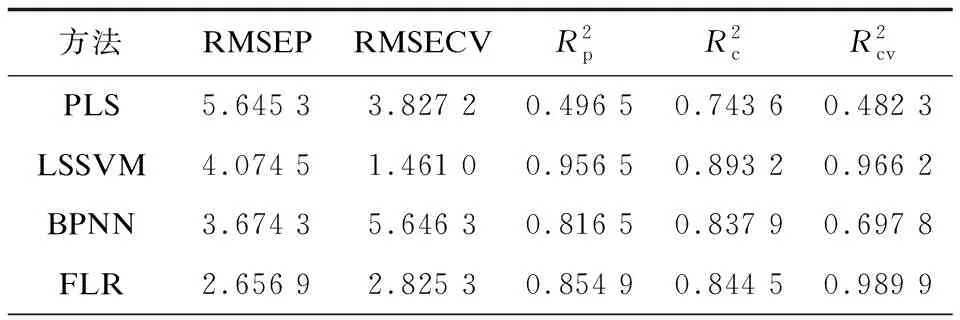
表1 高糖溶液浓度为30 mM环境下的预测结果

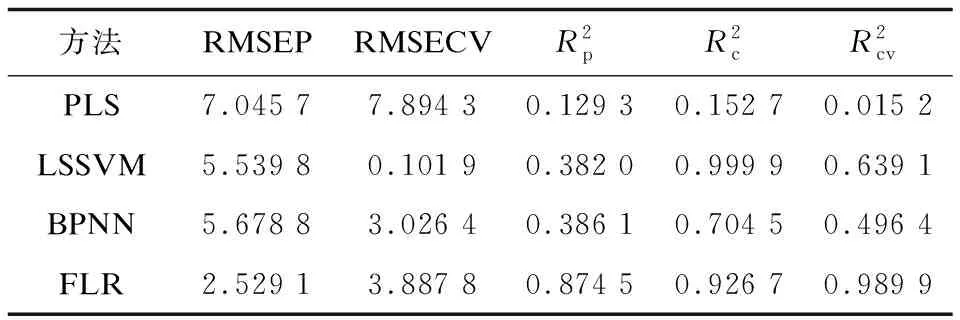
表2 高糖溶液浓度为40 mM环境下的预测结果
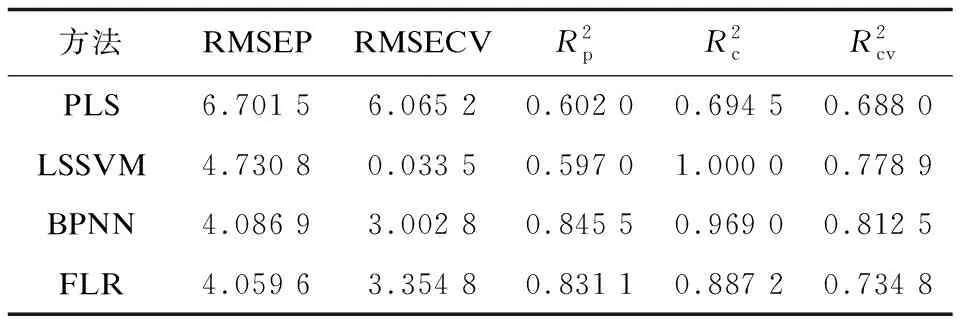
表3 高糖溶液浓度为50 mM环境下的预测结果
在表1~3中,均方根误差可以直观反映出模型的预测精度[17],该参数越小,说明预测精度越高。相关系数平方可以反映出实验数据输入与输出的相关性,该参数越大,说明模型的输入与输出相关程度越高。四种方法各自的预测精度在30 mM高糖环境中均相对较高,说明在此环境下,实验测量信号特征值变化最明显。在每种浓度下,文中使用的基于模糊规则的预测模型预测精度均为最高,说明该预测模型最适合用于对不同浓度急性高血糖作用时间的判断。
使用同样的思路,当已知急性高血糖作用时间时,可以预测血糖浓度,预测结果见表4。
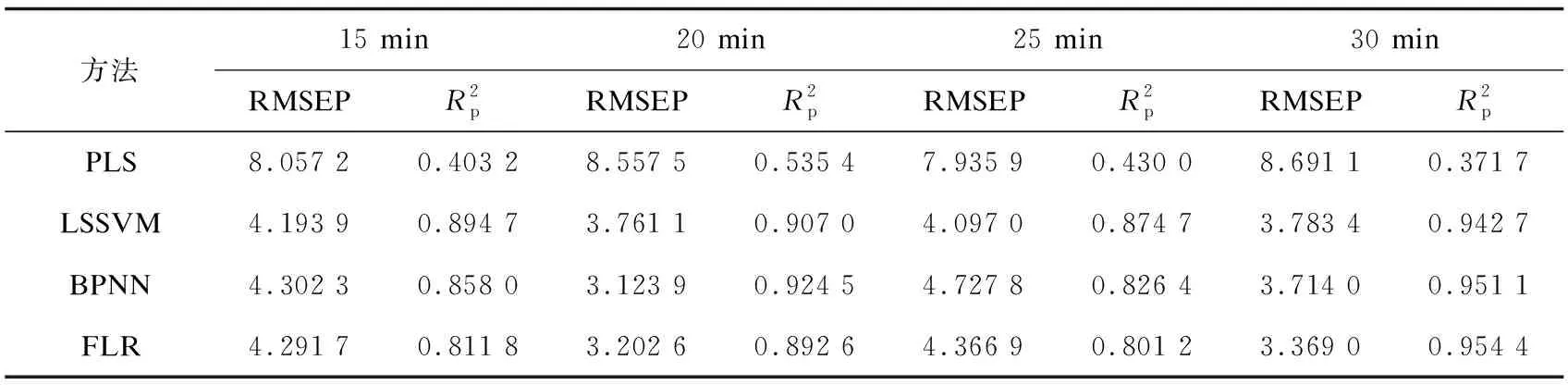
表4 已知急性高糖作用时间时对高糖浓度的预测结果
4 结束语
文中使用基于模糊规则的预测模型,通过分析心脏传导系统的电生理信息,实现了对不同浓度急性高血糖作用时间的预测。与三种经典的预测模型相比较,基于模糊规则的预测模型最适合用于急性高血糖作用时间的预测。未来应研究如何减少模型的时间和空间复杂度,对模型建立过程进行优化,并研究如何提取与急性高血糖有密切关系的体表生物的电信号,使该方法可以为急性高血糖的临床医学诊断提供指导与建议。
