具有二次预警行为的复杂网络病毒传播分析
2019-02-25张传宗朱阿康谢梦玮鲁延玲
张传宗,朱阿康,谢梦玮,鲁延玲
(南京邮电大学 理学院,江苏 南京 210003)
0 引 言
复杂网络[1]是具有众多数量节点和复杂连接结构的高度复杂的网络,可以看作是一个具有足够复杂拓扑结构的图,衍生出来小世界网络和无标度网络等网络模型[2]。众多复杂网络中,社会网络的研究已有很长的历史,它是由一群人或团体按照某种关系连接起来而构成的一种复杂体系。
病毒传播在社会网络中广泛存在,近年来,许多学者采用平均场[3]、有效度[4]、离散概率模型[5]等方法来描述病毒传播的演化过程,提出了包括SI、SIS和SIR在内的多种病毒传播模型[6-9],研究了不同病毒传播模型分别在均匀网络和无标度网络中的传播临界值问题[10-12]、动态网络中病毒传播模型的稳定性[13-14]等。
病毒在社会网络中传播时,人类会做出相应的行为反应,以减少自身被感染的概率。Sahneh和Scoglio在模拟病毒传播中的人类行为时,提出了SAIS病毒传播模型[15]。病毒正在传播的信息被健康节点获得后,健康节点的警觉意识就会促使它以一定的概率转化为预警节点,采取一些措施,降低自己被感染的可能性。而预警节点被感染后,经过一系列措施又恢复到健康状态,由于存在被感染的经历,所以经过一次预警行为的部分健康个体为了降低再次感染的概率,再次转化为预警节点,这就是二次预警行为,据此提出一种具有二次预警行为的SAIS模型。
1 基于二次预警行为的SAIS病毒传播模型
在网络拓扑结构中,个体用节点表示,个体间的连接关系用两节点间的边表示。在网络中,影响节点状态的因素不仅来自节点本身,也来自与其相邻的所有节点。在具有二次预警行为的SAIS病毒传播模型中,网络中的节点具有三种状态:健康状态S(易感染状态)、预警状态A(不易感染状态)、感染状态I。假设易感染节点被感染的概率为β0,预警节点被感染的概率为βα。在病毒传播过程中,由于预警节点会采取一定的措施降低被感染的概率,所以一般有:β0>βα。同时,易染节点以概率α转化为预警状态,感染节点以概率δ0恢复为易感染节点S,以δα的概率转化为预警节点。将感染节点转化为预警节点的行为称为二次预警。具有二次预警行为的SAIS病毒传播模型的节点状态转化示意图如图1所示。

图1 节点状态转化
设在一个节点平均度为
A+S+I=1
(1)
利用平均场理论,得到具有二次预警行为SAIS模型的微分动力学演化方程:
(2)
利用归一化条件,则上述微分方程等价为:
(3)
设D={(S,I)|0≤S,I≤1}为非负初始条件下的非负不变集。
2 病毒传播模型的理论分析
2.1 模型的求解
当病毒的传播进入稳态时,S、A、I三种节点密度随时间的变化率均为0,即dS/dt=0和dI/dt=0。此时,可以得到系统(3)的平衡点E=(S,I)⊂D。因此,平衡点满足:
(4)
由式4可知,显然,无病平衡点:E0=(S0,I0)=(1,0)是方程的一个平衡点。
当感染节点密度不为0时,即I≠0,则系统(3)地方病平衡点:E*=(S*,I*)满足方程:
β0
δαI-δ0I=0
(5)
-β0
(6)
由式5得易感染节点平均密度与感染节点平均密度的关系式为:
(7)
将式7带入式6得稳态时感染节点密度:
(8)
则易感染状态节点密度为:
(9)
即可以得到结论:系统(3)存在唯一地方病平衡点。
由以上结果易得具有二次预警行为的SAIS模型的病毒传播阈值为:
(10)
2.2 结果分析
2.2.1 分析旧模型
使用同样的求解方法,对具有一次预警行为的SAIS模型及经典SIS模型进行求解,得到如下结果:
具有一次预警行为的SAIS模型:
经典SIS模型
2.2.2 感染节点密度的比较
从求解结果来看,显然有I
(1)比较I'与I''。
利用已求的感染节点密度分析得:
即当β0>βα时,I'
(2)比较I与I''。
利用已求的感染节点密度分析得:
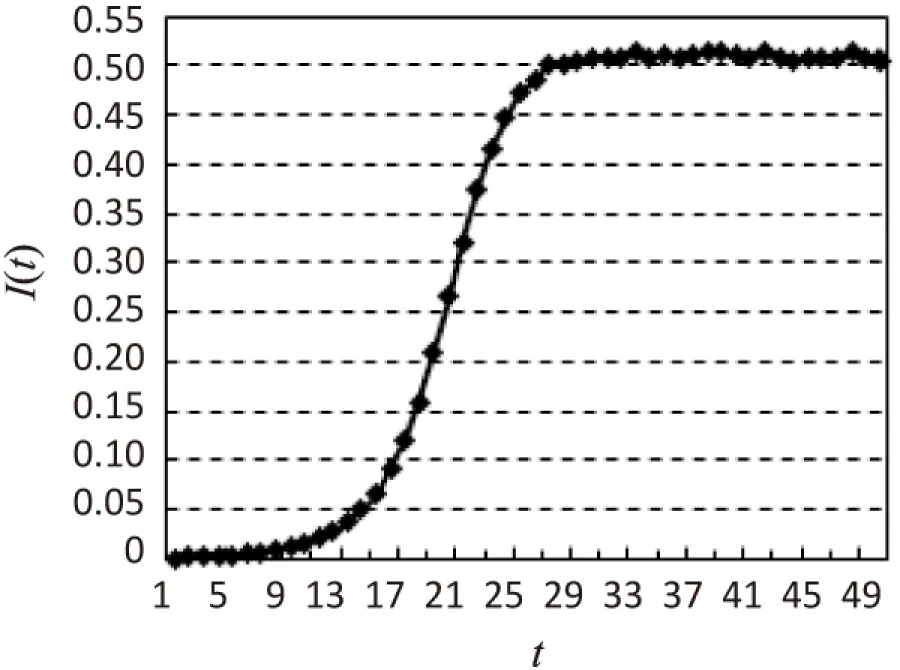
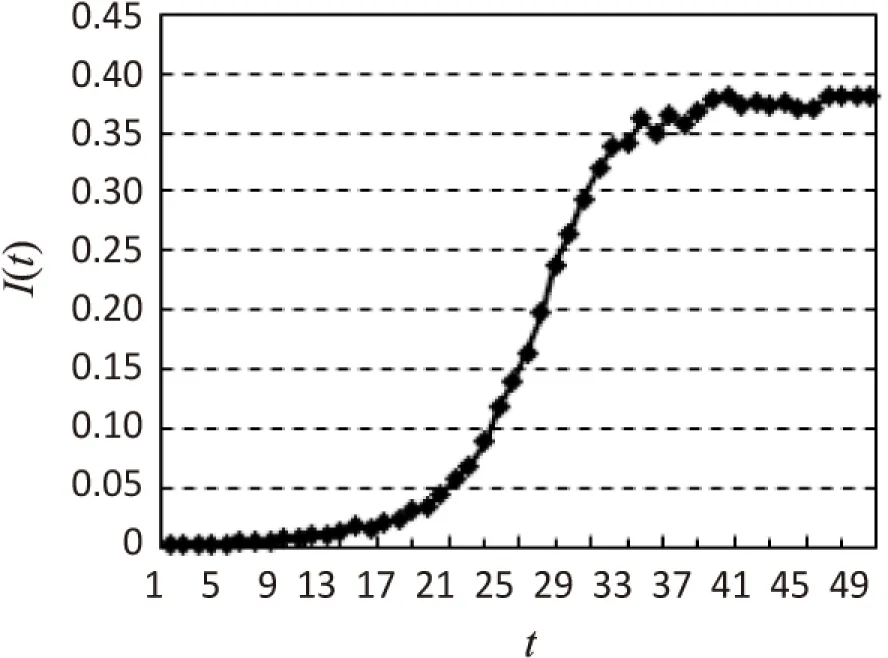
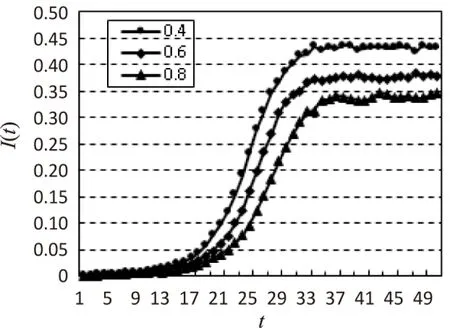
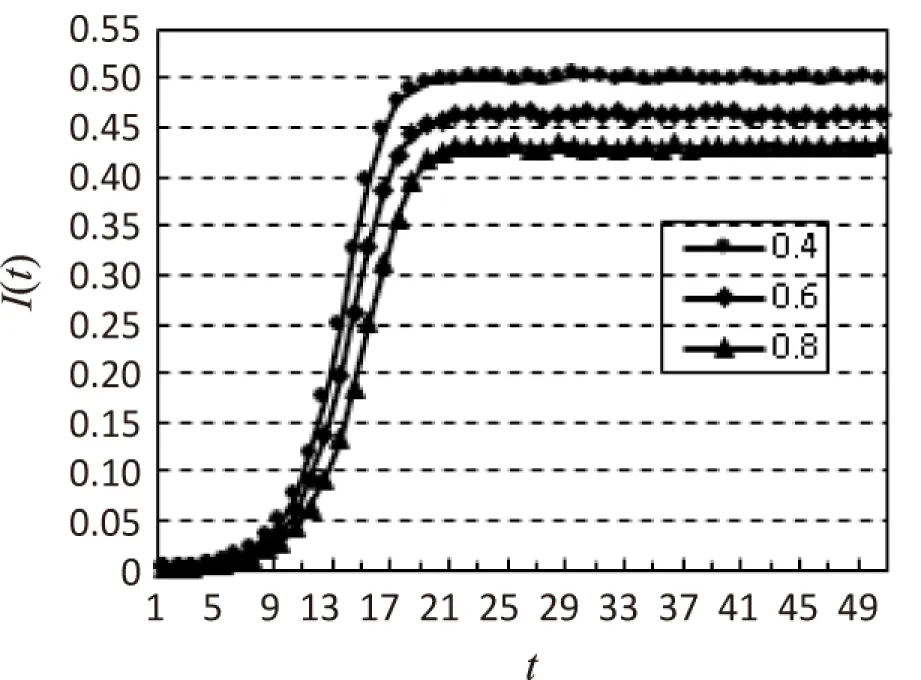
显然,若β0>βα时,I 得到以下结论: 定理1: (1)当β0>βα时,I 注:相比于具有一次预警行为的SAIS模型,加入了二次预警的SAIS模型的感染节点密度小于SIS模型的感染节点密度时,预警节点被感染的概率所取范围更广。 2.2.3 传播阈值的比较 通过不同模型的传播阈值的比较,可以更好地体现模型的优越性。 对上式的正负性进行讨论后,可以得出结论: 定理2: 注:相比于具有一次预警行为的SAIS模型,加入了二次预警的SAIS模型的传播阈值小于SIS模型的传播阈值时,变量取值范围更广。 根据理论分析可以发现,随着二次预警率的增加,感染密度逐渐减小,病毒传播临界值逐渐增大。 在WS小世界网络中进行仿真,以验证理论结果。WS小世界网络中的节点数为1 000,节点的平均度 在小世界网络中,在相同的条件下模拟具有二次预警行为与具有一次预警行为的SAIS模型感染节点密度与时间的变化关系,如图2和图3所示。 图2 有一次预警行为的SAIS模型感染节点密度与时间变化曲线 由图2可以看出,随着时间的推移,病毒传播呈现先上升后趋于稳定的形态。最终感染节点密度稳定在0.5左右。 由图3可以看出,随着时间的推移,病毒传播呈现先上升后趋于稳定的形态。最终感染节点密度稳定在0.35左右。 从图2及图3的感染节点密度走向上看,两种模型最终都会趋于一个稳定值。对比两幅图像,显然增加了第二次预警行为的SAIS模型的稳态感染节点密度要小于仅具有一次预警行为的SAIS模型。符合理论推导。 图3 具有二次预警行为的SAIS模型感染节点密度与时间变化曲线 针对不同感染率,改变二次预警率,得到不同预警率下感染节点密度随时间变化的曲线。当易染节点被感染的概率β0=0.02,二次预警率分别取值0.4,0.6,0.8时,稳态感染节点密度随时间变化的曲线如图4所示。 图4 不同二次预警率对I(t)的影响(β0=0.02) 由图4可以看出,随着病毒传播时间的推移,感染节点密度均会趋于一个稳定的数值,且二次预警率越高,稳态时感染节点密度越低。 当易染节点被感染的概率β0=0.08,二次预警率分别取值0.4,0.6,0.8时,稳态感染节点密度随时间变化的示意图如图5所示。 图5 不同二次预警率对I(t)的影响(β0=0.08) 从图5中可以得出与图4相同的结论,即二次预警率越高,稳态时感染节点密度越低,感染节点的数目越少。 综上所述,随着二次预警率的增加,稳态时感染节点的密度不断减小。而且二次预警率越高,病毒传播进入稳态的时间越短。从而可以说明增加二次预警率可以减少病毒爆发规模,减缓病毒在网络中的爆发。 在实际社会网络中,健康个体即使采取一定措施转化为预警个体,可最后还是感染病毒转化为感染个体;随着自身康复力和外部治疗的作用,感染个体被治愈,由于之前的染病经历,该个体又重新回到预警状态。文中正是考虑人类的二次预警行为,提出了新的SAIS病毒传播模型。在该模型中,一方面,健康节点可以接收到感染邻居节点散布的“病毒存在”预警信息,进而以一定的预警率转化为预警节点;另一方面,感染个体被治愈后,由于种种原因对预警行为有记忆,可以直接转化为预警个体。理论分析和研究发现,随着二次预警率的增加,感染密度是逐渐变小的,病毒传播临界值是逐渐增大的,说明随着二次预警率的增加,可以减少病毒爆发规模,减缓病毒在网络中的爆发。 这意味着,预警信息的重视程度越强,二次预警行为越普遍,越可以减缓病毒在网络中的传播,进而降低病毒爆发的规模。为了更好地预防和控制病毒传播,病毒传播过程中的预警行为对病毒传播的影响,以及预警行为和病毒传播的相互关系值得继续深入研究。
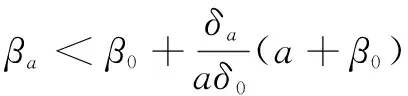
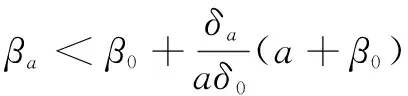
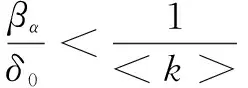

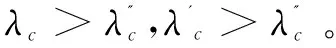
3 数值仿真
3.1 验证理论结果
3.2 研究二次预警行为模型的性质
4 结束语
