MATLAB软件在量子力学教学中的应用

钟志有，龙 浩

(中南民族大学 电子信息工程学院，湖北 武汉 430074)

1 引言

量子力学是普通高等院校许多理工科专业的一门学科基础必修课程，它不仅被认为是现代物理学的两大基本支柱之一，而且被广泛应用于化学、材料学、生物学和宇宙学等有关学科和许多近代技术之中[1～6]。量子力学是反映分子、原子、原子核和基本粒子等微观粒子运动规律的理论，是一门建立在公理体系上的科学，对初学者来说，人们普遍感到量子力学的概念抽象、理论性强、数学难度大、计算繁琐、做题时束手无策，学习和掌握该课程的困难非常大[7～10]，因此教学效果不如人意。众所周知，作为目前最为流行的数学工具软件之一，MATLAB不仅具有强大的数值计算能力和功能齐备的可视化能力[11～15]，而且还具有简单易学、运算效率高、应用范围广等特点，它在众多领域得到了广泛应用[16～20]。本文中，以一维谐振子和矩阵运算作为实例，阐述了MATLAB软件在量子力学教学中的应用，实践表明MATLAB的引入对于提高学生学习兴趣和教学质量具有事半功倍的作用。

2 一维谐振子

自然界中常见的简谐运动，任何体系在平衡位置附近的小振动(如分子的振动、晶格的振动、辐射场的振动等)，在选择合适的坐标之后，常常可以分解为若干个彼此独立的一维谐振动；另外，谐振动还可以作为复杂运动的初步近似。因此，对于谐振子的研究，无论是在理论上还是在应用上都是非常重要的[1,2]。

设一维谐振子的势能U(x)=mω2x2/2，则对应的定态Schrödinger方程为:

(1)

令方程(1)可化为:

ψ(ζ)″+(λ-ζ2)ψ(ζ)=0

(2)

对于方程(2)，当时，满足有限性条件的渐近解为。再令，方程(2)可表示为：

H(ζ)″-2ζH(ζ)+(λ-1)H(ζ)=0

(3)

方程(3)称为Hermite方程。当满足关系式(=0，1，2，)时，其解为Hermitian多项式。综上可以得到一维谐振子的能级为:

(4)

由式(4)看出，一维谐振子的能级是分立的，并且是均匀分布的，两个相邻能级之间的间距为。对应能量，一维谐振子波函数为:

(5)

根据式(5)，一维谐振子的概率密度可以表示为:

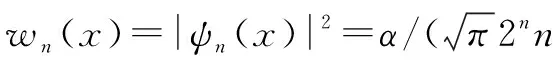
(6)

当n取值比较大时，Hn(αx)的表达式是非常复杂的，因此很难直观讨论波函数的物理意义。

基于公式(5)和(6)，利用MATLAB软件编写程序绘制出ψn(x)和wn(x)的分布图像，如图1所示。由图可见，一维谐振子的波函数ψn(x)与横坐标相交n次，即存在有n个节点。另外，概率密度wn(x)不仅随x变化而变化，同时其值也与量子数n密切相关。MATLAB模拟结果与理论分析是完全相符的[1,5]。

3 矩阵运算

在量子力学中，当力学量算符和态矢量采用矩阵表示后，相应的公式和方程也可以通过矩阵进行描述[1,16]。在所研究的问题中，当所选表象的基矢量个数较少时，那么力学量算符和态矢量矩阵的维数较小，计算过程就相对简单；但是当基矢量个数较多时，那么力学量算符和态矢量矩阵的维数就较大，因此计算复杂、工作量大。这时如果借助MATLAB软件就可以使学生从枯燥繁琐的计算过程中解脱出来，从而有利于调动他们的学习积极性、提高学习效率[21～25]。

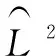
(7)

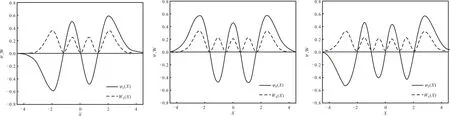
图1不同量子数时的波函数和概率密度曲线(取α=1)

从上述计算过程来看，求解这类问题不仅要求数学基础好、演算能力强，同时计算工作量也非常之大。但利用MATLAB软件进行处理，只要通过命令[V, D]=eig(A)就能得到矩阵A的本征值和相应的本征态。对于本题，只需在MATLAB的Command Window中输入如下指令，就能获得结果，如图2所示。

图2 Command Window中输入的指令和运行结果

从图2显示的结果看出，程序运行不仅得到了算符的本征值，而且还得到了它们对应的本征函数，最后只需利用归一化条件对本征函数进行归一化就行了。很明显，采用MATLAB软件时，计算工作量大大减少。

4 结语

量子力学是反映微观粒子运动规律的理论，是人们认识物质世界的思维方式和表达方式。本文针对学生在量子力学学习中所存在困难，通过引入MATLAB软件进行绘图和科学计算，从而使计算复杂的内容得以简化，同时也使抽象难懂的内容得以形象化，因此，这不仅有利于在教学过程中简化理论计算过程、强化物理实质讲解，同时还能够更好地调动学生学习量子力学的积极性，有效提高量子力学的教学质量。