航姿系统矢量场传感器的完全校正

李 翔，刘耀华，宋百麒

(桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004)

0 引言

三轴磁强计与三轴加速度计广泛应用于航姿系统(AHRS)以及电子罗盘中，通过测量地磁矢量和重力矢量可实现姿态与方位(航向)的解算。然而由于制造工艺,安装误差及环境因素等影响，三轴磁强计与加速度计在使用中必须进行误差校正与补偿，以保证航姿系统的精度[1]。

目前，航姿系统中的磁强计和加速度计校正普遍采用基于椭球拟合的校正方法[2-6]，该方法只利用磁强计和加速度计的原始测量数据即可实现校正，便于使用者在各种应用场合进行快速、便捷的现场校正[7-10]。然而，椭球拟合法校正后的传感器坐标系不能保证与载体坐标系相重合[11-15]，这将对航姿系统造成不可忽视的影响。

本文在对椭球拟合法的原理及其缺点进行理论分析的基础上，提出一种补偿传感器非对准误差的改进方法。实验表明，该方法能实现磁强计与加速度计的完全校正，减小地磁和重力矢量的测量误差，改善航姿系统的精度。

1 传感器误差模型

三轴磁强计及三轴加速度计通常采用的误差模型：

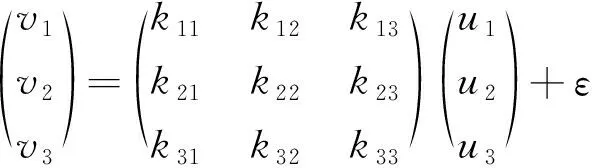
(1)

式中:三维矢量u=(u1u2u3)T表示被测矢量(地磁矢量或重力矢量)；三维矢量v=(v1v2v3)T代表传感器输出；3×3矩阵K=(kij)3×3用于描述灵敏度(标度系数)误差、非正交误差、安装误差及磁强计受到的软磁干扰等；噪声项ε一般假定为零均值高斯白噪声。

式(1)给出的线性误差模型能满足一般用途的精度要求。若忽略式(1)中的噪声项并记L=K-1，则有

u=L(v-b)

(2)

式中矢量b=(b1b2b3)T描述传感器的常值误差(零偏)，对磁强计而言b还包含硬磁干扰。

由式(2)即可实现三轴磁强计或加速度计的误差补偿。

2 椭球拟合法概述

任一固定地点的地磁场强度和重力加速度在短时间内可认为保持不变，因而地磁矢量及重力矢量的模值均为常数，这一性质可用下式来描述：

‖u‖=‖L(v-b)‖=u0

(3)

式中u0为矢量u的2-范数即欧氏范数。对式(3)取平方，可得到一个关于矢量(v-b)的二次型：

(v-b)TLTL(v-b)=‖u‖2

(4)

引入式(2)时已假定了K可逆，则L=K-1亦可逆，从而LTL对称正定，即式(4)是一个代表椭球面的二次型。因此，凡是基于式(4)的校正方法，无论采取何种具体算法，本质上都是在拟合该式所代表的椭球面，故统称为椭球拟合法。

由式(4)可知，椭球拟合法只需利用传感器自身读数，完全不需要传感器载体的姿态信息。故椭球拟合法的最大优点是不需外部设备或基准即可实施校正。椭球拟合法的另一优点是能使被测矢量的模值误差最小化，这是由式(4)的本质决定的。

然而，由于椭球拟合法在校正过程中完全忽略了三维姿态信息，因此不能保证传感器坐标系与载体坐标系重合，两坐标系间通常存在未完全补偿的非对准误差，从而导致被测矢量出现指向误差，影响航姿系统的精度。

3 非对准误差及其校正

三轴磁强计或加速度计的非对准误差可用一个三阶正交矩阵R描述，该矩阵的几何意义是从传感器坐标系到载体坐标系的三维旋转变换。引入矩阵R后，按下式进行传感器误差补偿。

u=RL(v-b)

(5)

目前采用较多的求取R的方法是利用地磁矢量与重力矢量的夹角[12-15]。若磁强计与加速度计均已由椭球拟合法校正，并记二者读数分别为h与g(均为三维矢量)，由于地磁矢量与重力矢量夹角恒定(记为γ)，二者的点积应为常数，即

gTRh=g0h0cosγ

(6)

式中g0，h0分别为本地重力加速度与地磁场强度。由式(6)可求解R，称为“常数夹角法”[12]。但此方法仅能求出磁强计坐标系到加速度计坐标系的正交矩阵，亦即只能实现两传感器之间的对准，而不能补偿传感器与载体坐标系之间的非对准误差。

4 改进的校正方法

采用二步法实现三轴磁强计及加速度计的完全校正，即先用椭球拟合法确定式⑵中的L与b，再求解正交矩阵R。以下重点讨论R的求法。

假定传感器已由椭球拟合法校正，将其绕某一固定轴转动时，被测矢量u在该转轴上的投影应保持不变。记沿该转轴方向的单位矢量为e，u与e夹角为λ，则有

eTu=eTRL(v-b)=u0cosλ

(7)

利用式⑺即可求解矩阵R，从而补偿传感器非对准误差，但需注意以下几点：

1) 旋转轴e不应与被测矢量u平行，否则旋转过程中传感器读数基本无变化，无法求解矩阵R。

2) 旋转轴e一旦选定，数据采集过程中应保持其指向不变，以保证式(7)成立。

3) 为保证采样数据的充分性[16-17]，应将传感器置于至少3种不同姿态下分别绕转轴e旋转。如依次将航姿系统的x、y、z轴指向正东，并分别绕轴转动1周，采集到的磁强计和加速度计读数便可满足以上要求。且按上述要求采集的数据也适用于椭球拟合法，亦即两步校正可共用同一组数据集而无需再次采样。

4) 旋转轴e需以载体坐标系下的分量形式代入式⑺，方能实现传感器与载体坐标系之间非对准误差的补偿。如按3)所述方式采集的数据，转轴e在载体坐标系中的指向依次为e1=(1 0 0)T，e2=(0 1 0)T，e3=(0 0 1)T。

5) 矩阵R虽含9个元素，但由于正交性的约束，实际只有3个独立参数，即分别绕3个坐标轴的旋转角度δ1、δ2和δ3。又考虑到非正交误差通常较小，故可采用下式所示的近似形式以简化计算。

(8)

5 实物验证

5.1 实验器材

采用图1所示基于MPU9250芯片的航姿模块验证本文提出的校正方法。MPU9250芯片内部均含加速度计、磁强计和陀螺仪3种传感器。航姿模块的x、y、z轴定义已在图1中标出。

图1 航姿模块

5.2 数据采集与校正

实验中，采集磁强计和加速度计读数的步骤为：

1) 航姿模块y轴指北并绕其旋转1周。

2) 航姿模块z轴指北并绕其旋转1周。

3) 航姿模块z轴指南并绕其旋转1周。

在这3种姿态下，转轴e在载体坐标系中的指向依次为e1=(0 1 0)T，e2=(0 0 1)T，e3=(0 0 -1)T。

上述操作过程无需专门设备，只需将图1所示航姿模块的侧面、底面和顶面分别紧贴在同一直立平整墙面上并旋转即可，对墙面的朝向无严格要求。采集到的三维地磁数据如图2所示。

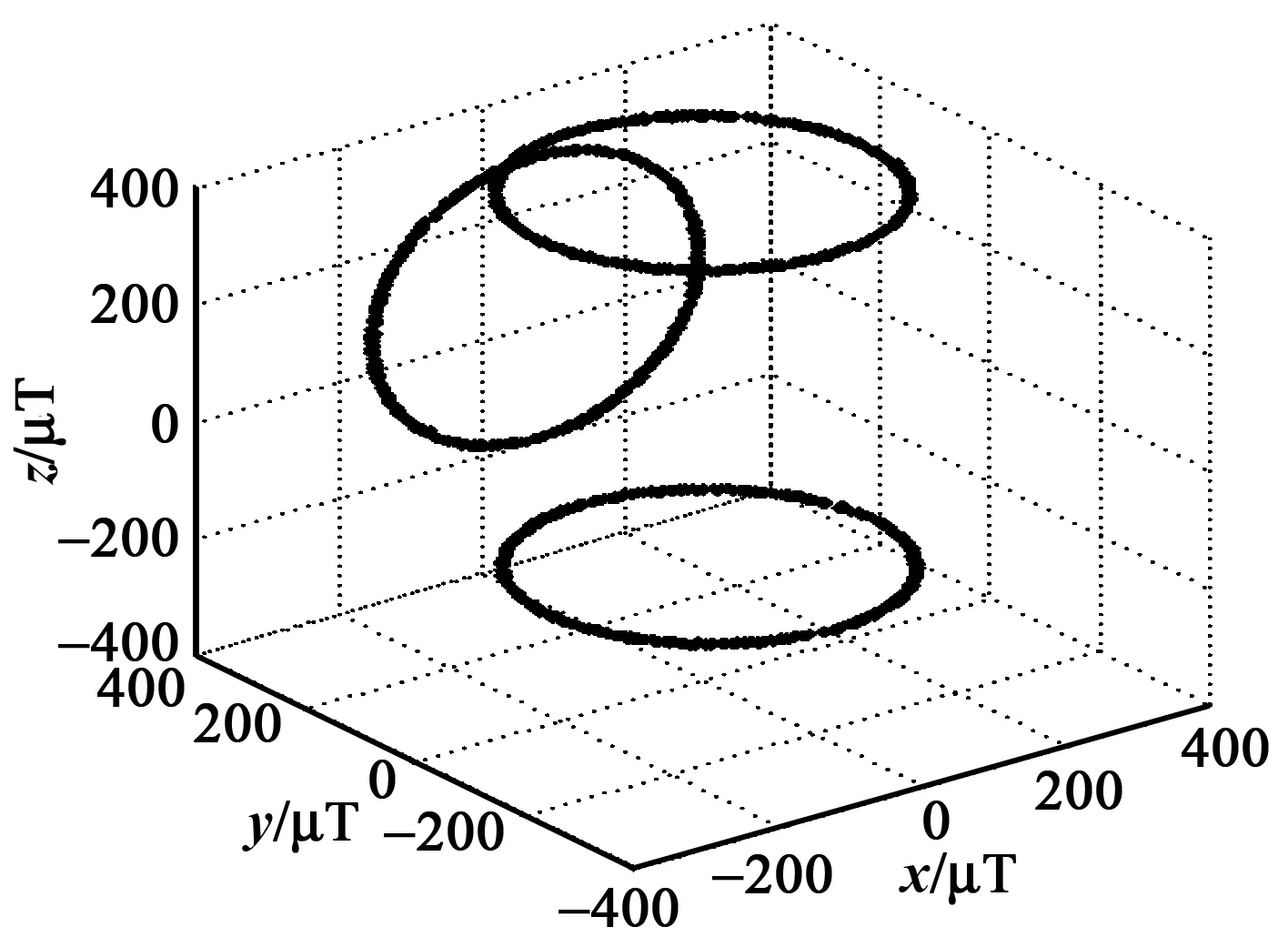
图2 地磁场采样数据

完成数据采集后，分别采用下列3种方法对磁强计和加速度计进行校正：

方法1：磁强计和加速度计各自采用椭球拟合法进行校正。

方法2：先用椭球拟合法分别校正磁强计和加速度计，再对磁强计采用常数夹角法。

方法3：采用第4节所述二步法，分别对磁强计和加速度计进行校正。

5.3 实验结果

分别采用上述3种方法对航姿模块进行校正后，再利用三轴转台(角度分辨率0.1°)检验该模块输出的航向角、俯仰角及横滚角的准确性。图3～5分别为航向角、俯仰角、横滚角的误差曲线。

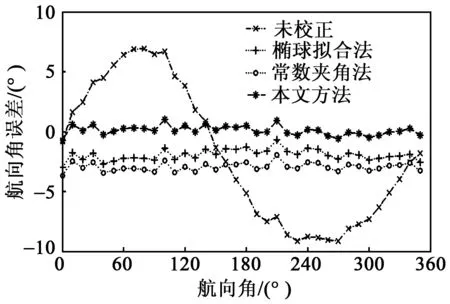
图3 航向角误差曲线

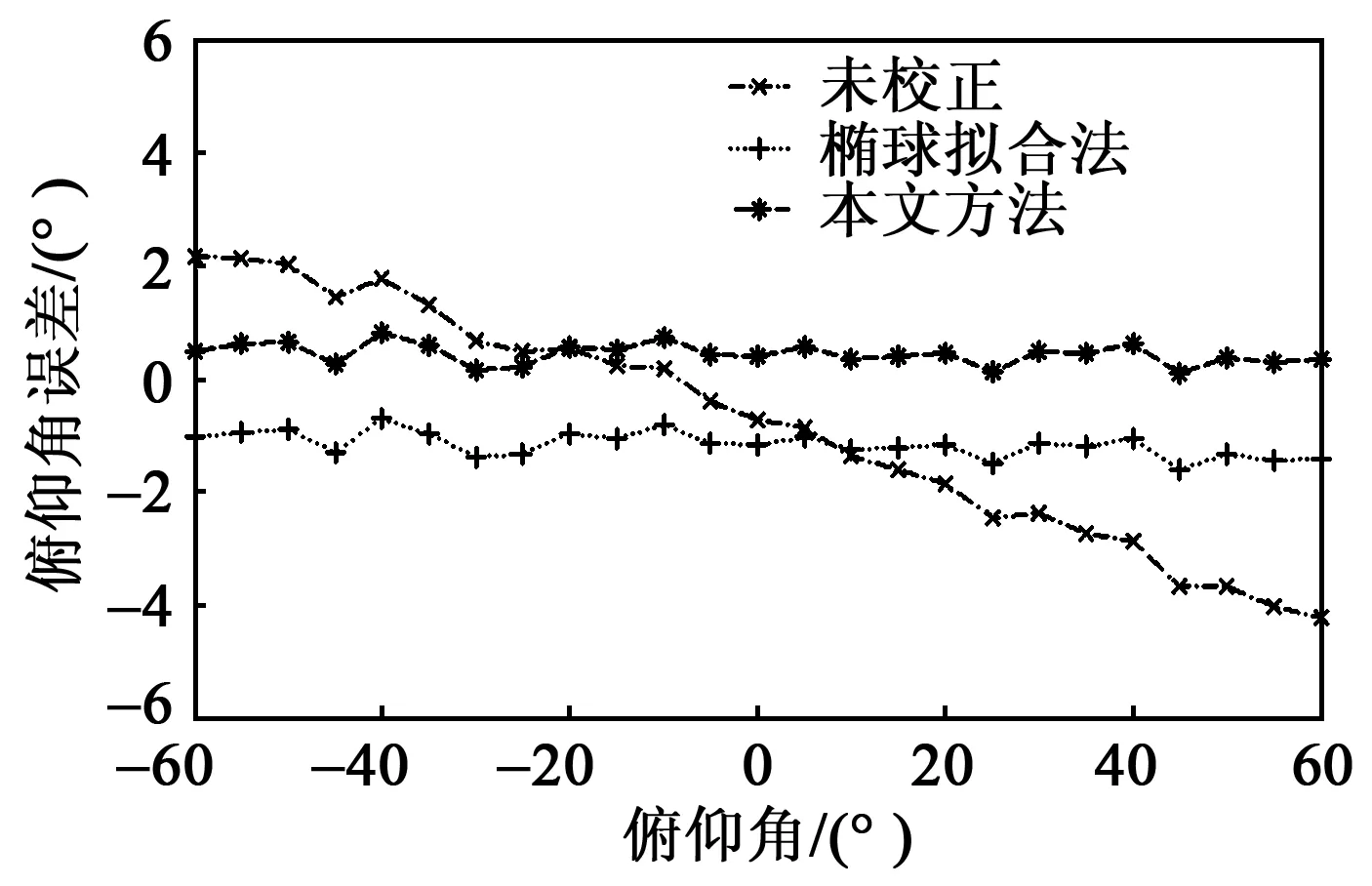
图4 俯仰角误差曲线

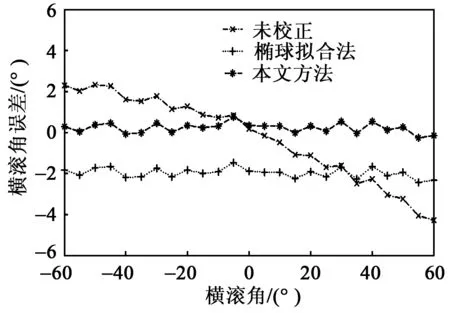
图5 横滚角误差曲线

由图3～5可见，本文所介绍的校正方法能在椭球拟合法的基础上进一步提高航姿系统的精度。通过表1给出的校正前、后的角度误差统计结果可更明显地看出这一点。

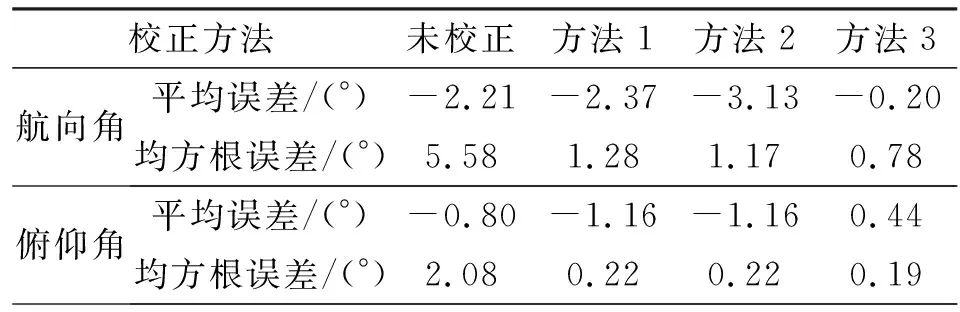
表1 角度误差统计

续表

校正方法未校正方法1方法2方法3横滚角平均误差/(°)-0.27-1.97-1.970.22均方根误差/(°)2.090.240.240.24

表1中所列均方根误差用于评价角度数据的均匀性，而平均误差则主要反映由传感器非对准误差引起的角度固定偏差。

由表1可见，校正方法1(椭球拟合法)和方法2(常数夹角法)具有较小的均方根误差，亦即这两种方法能改善角度的均匀性。然而角度的平均误差相对于校正前反而有所增大，表明校正后仍存在非对准误差导致的固定偏差，这与图3～5所示误差曲线相吻合。

与校正方法1、2相比，校正方法3(即本文方法)的均方根误差及平均误差都较小，表明传感器的非对准误差得到了较好的补偿。

6 结束语

针对椭球拟合法校正后遗留的传感器非对准误差，本文提出的改进校正方法能对其进行较好的补偿，从而实现三轴磁强计和加速度计的完全校正，且校正过程操作简便。实验结果表明，采用本文方法校正后，航姿系统的角度平均误差及均方根误差均能减小至1°以内，可显著提高其精度。