基于钝化微分的压电微动平台PID控制

刘尔春，孙庆龙，卢志诚，惠相君，周鹏飞，汪家乐，孙靖康，崔玉国

(1.宁波大学 机械工程与力学学院，浙江 宁波 315211; 2.首信自动化有限公司，河北 迁安 064400)

0 引言

压电微动平台是一种由压电执行器驱动的微位移机构，具有结构小巧紧凑,输出力大,分辨率高,响应速度快及负载能力强的特点，因而被广泛应用于高精密定位系统中。如在超精密加工中，它可以推动刀架使刀具实现微移动，进而使加工更精准[1]；在微结构表面形貌测量中，它可以作为扫描探针显微镜的扫描平台，进而和微探针相配合，实现对微结构表面的精密测量[2]；在微机电系统(MEMS)装配中，它可作为微零件、微部件的载物台，带动微零件、微部件产生微运动，从而在微机器人操作手的配合下，将微零件装配成微部件，或将微部件装配成微系统[3]。另一方面，由于压电执行器存在迟滞误差特性，会使由其驱动的微动平台产生定位误差，因此需要采取相应的控制方法对平台进行控制，如前馈控制[4]、比例、积分、微分(PID)控制[5-7]、鲁棒控制[8]、自适应控制[9]、复合控制[10-11]等。宋林等基于所提出的阈值优化Prandtl-Ishilinskii(PI)迟滞模型，设计了压电微动平台的前馈控制器，平台在前馈控制作用下，达到5 μm阶跃参考位移的响应时间为0.01 s，跟踪最大值为17 μm的变幅值三角波参考位移时，使定位误差变化范围由-1.15～1.35 μm减小为-1.15～-0.05 μm[4]。Lin等采用灰色相关分析法来整定压电微动平台的PID控制器参数，使平台在PID控制下的稳态误差减小了97%[6]。Ghafarirad等将基于改进观测器的鲁棒控制同PI逆模型相结合，设计了压电微动平台的鲁棒控制器，实现了平台在预估干扰作用下的精密定位[8]。张桂林等基于传统PI迟滞模型来描述压电执行器的迟滞特性，并采用自适应投影法来在线辨识压电执行器的PI迟滞模型，进而设计出了压电执行器的自适应PI逆控制器，使执行器的定位精度提高了49.8%[9]。Lin等将双前馈补偿与反馈控制相结合，设计出了压电微动平台的复合控制器，在复合控制作用下，平台沿x、y向的定位误差分别达到21.5 nm、20 nm[11]。

在上述这些控制方法中，前馈控制属于开环控制，无需传感器，系统构成简单，成本低，但因无反馈环节，很难实现平台的高精度定位。PID控制、鲁棒控制、自适应控制属于反馈控制，在对平台进行控制时，往往需要精密位移传感器，故成本较高，但能够实现平台的高精度、高分辨率定位。其中，PID控制技术最成熟，简单易用，且不需要被控对象的精确模型，故应用更广泛。复合控制可使平台获得良好的静、动态特性，但整个控制系统构成较复杂。

本文为提高压电微动平台的定位精度，并消除其工作过程中所受到的扰动或冲击(包括控制过程中的超调)，引入低通滤波器来降低PID控制器中微分环节对扰动或冲击的敏感性，进而来设计平台的PID反馈控制器，并实现平台的精密定位控制。

1 PID控制原理

PID控制通过对被控对象的偏差(即被控对象参考输入与实际输出的差值)进行比例(P)、积分(I)、微分(D)的线性运算，来实现对被控对象的控制，如图1所示。图中，s为复数变量，1/s、s分别为积分环节、微分环节。PID控制器的控制规律为

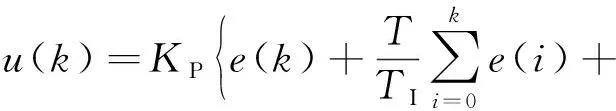
(1)

式中k=0, 1, 2,…为采样序号，即0,T, 2T,…采样时刻；u(k)为在kT采样时刻的控制量；e(k)、e(k-1)分别为在kT、(k-1)T采样时刻的偏差；KP、TI、TD分别为比例系数、积分时间常数、微分时间常数；T为采样周期。

图1 PID控制框图

式(1)给出的PID控制器的输出，包含了当前和以往所有时刻偏差的积分，这样会占用较大的计算机内存，使计算时间变长，被控对象的响应时间变慢。为此，本文采用具有递推关系的PID控制。由式(1)可得，PID控制器在(k-1)T时刻的输出为

(2)

将式(1)减去式(2)可得具有递推关系的PID表达式为

u(k)=u(k-1)+KP{e(k)-e(k-1)+

g1e(k-1)+g2e(k-2)

(3)

其中

(4)

(5)

(6)

由式(3)可知，具有递推关系的PID的控制量u(k)仅与u(k-1)、e(k)、e(k-1)、e(k-2)有关，不仅减小了计算机内存的占用量，且还可显著缩短计算时间，易于实现快速控制。

对式(3)两端同时进行z变换，可得具有递推关系的PID控制器的离散脉冲传递函数为

(7)

2 平台的改进PID控制器设计

2.1 平台控制器设计

在PID控制中，微分项能够提高系统的动态特性，缩短瞬态响应的过度过程，但其对干扰或冲击信号非常敏感，它会使干扰所引起的控制量变化幅度增大。对压电微动平台而言，控制量的这种大幅度变化不仅会造成平台定位精度的下降，有时还会使压电执行器及平台受到破坏。

干扰或冲击信号为高频信号，而低通滤波是去除高频干扰信号的有效方法。为此，本文在PID控制器中引入低通滤波器，以降低PID控制中微分环节对扰动或冲击信号的敏感性，即使微分环节对扰动或冲击产生钝化(见图2)。图中，E(s)为偏差e(t)的拉氏变换，U′(s)为PID控制器输出的拉氏变换，U(s)为低通滤波器输出的拉氏变换，τ′为低通滤波器的时间常数。

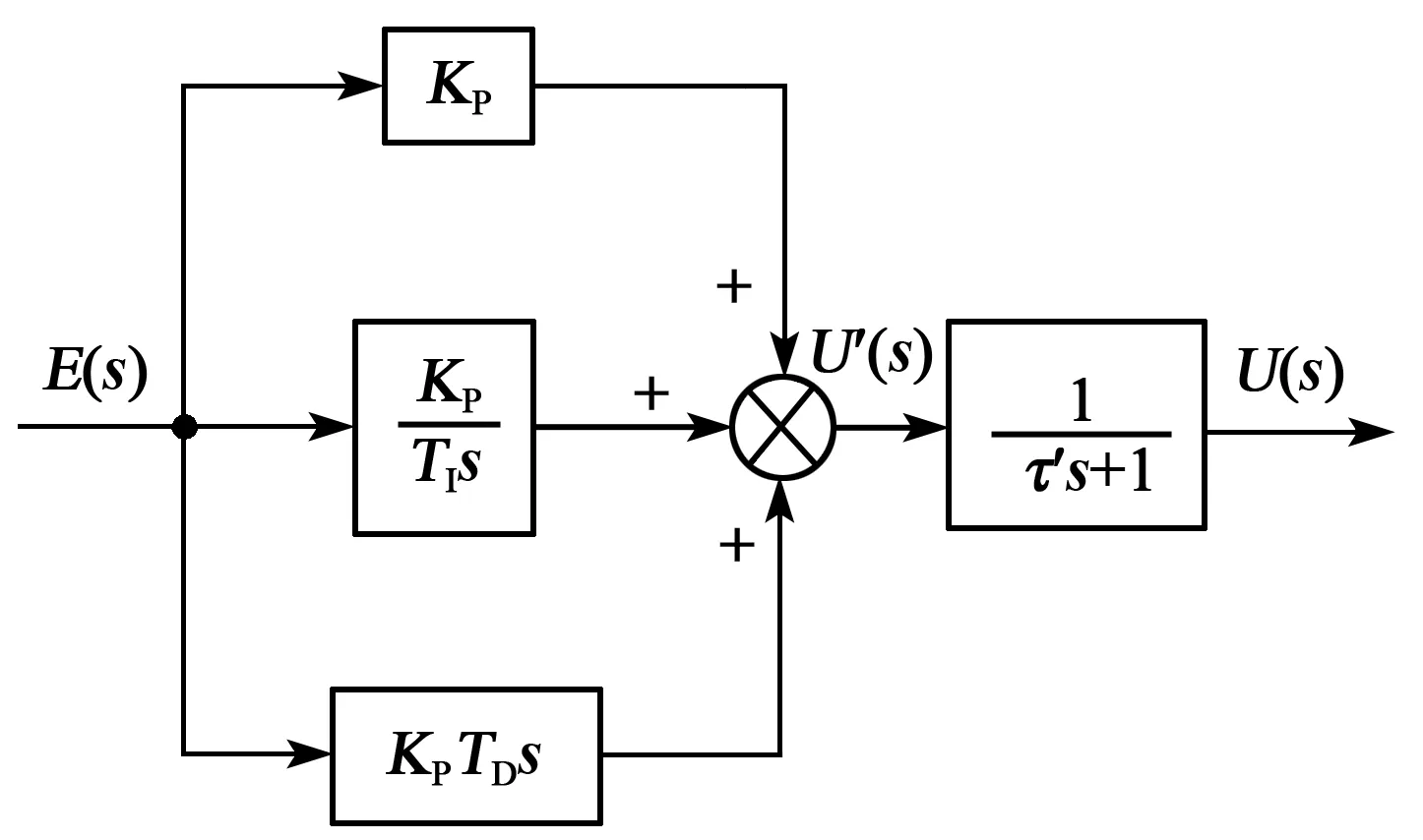
图2 钝化微分PID控制框图

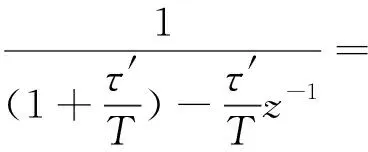
(8)

式中α为常数，且α<1，则有

(9)

于是，钝化微分PID控制器的离散脉冲传递函数为

(10)

2.2 平台控制系统仿真

基于所设计的平台改进PID控制器以及所建立的压电执行器与平台的动力学模型，设计出了平台的控制系统，其MATLAB/simulink仿真框图如图3所示。

图3 平台控制仿真框图

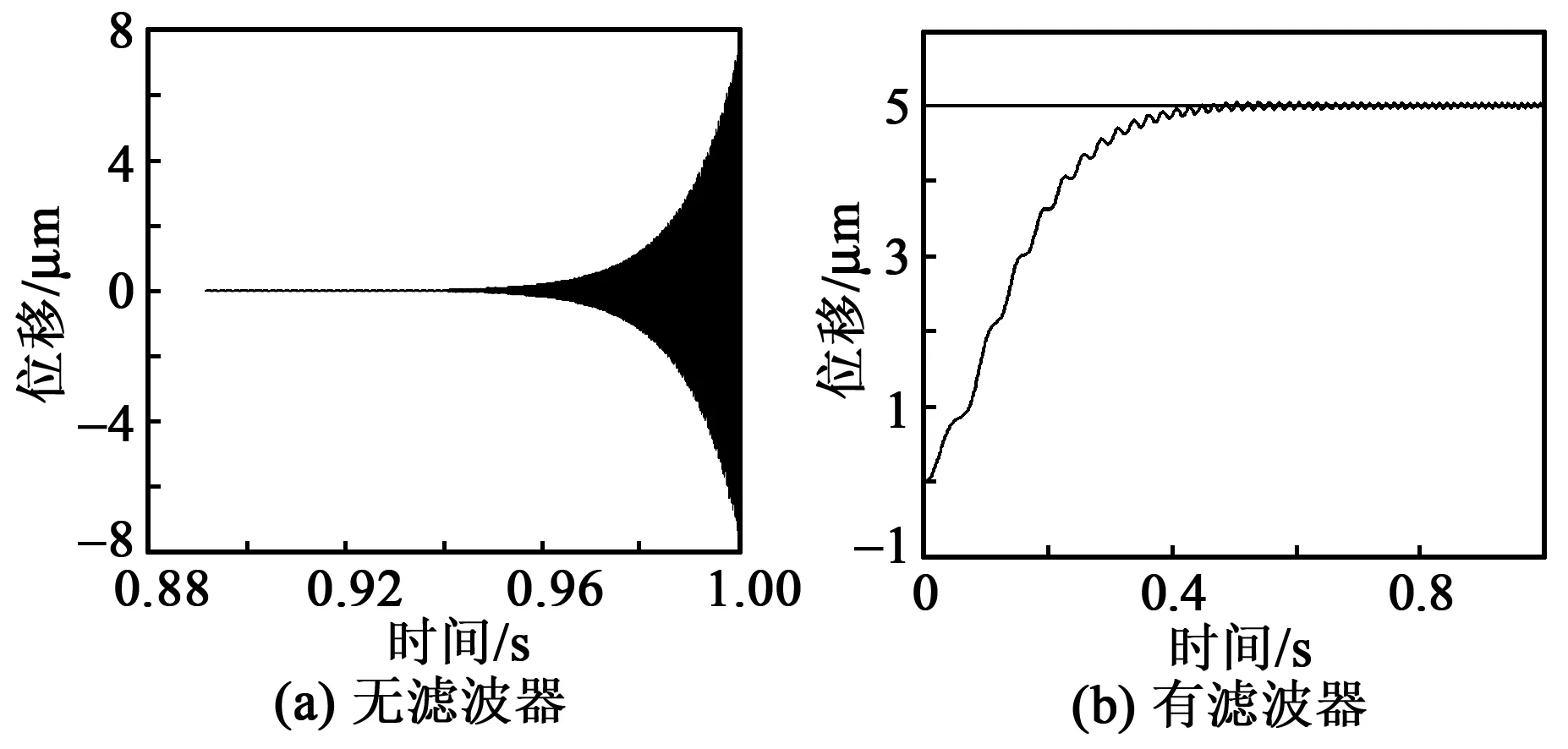
图4 滤波器对平台控制结果的影响

图4为平台在干扰(其幅值为0.5 μm，频率为10～100 Hz)作用下，对阶跃目标位移(其值为5 μm)的响应。其中，图4(a)为无滤波器时平台的响应，这时平台输出已不稳定；图4(b)为有滤波器时平台的响应，此时平台输出仍稳定，且无超调，也无稳态误差。可见，所设计的钝化PID控制器可有效消除干扰对平台输出位移的影响。

图5为平台在5 μm的阶跃目标位移且不受干扰的情况下，不同的KP、KI、KD对平台输出位移的影响。由图5(a)可知，随着KP(此时KI、KD均为0)的增大，平台响应加快，稳态误差减小，但KP太大时，平台输出位移会出现超调。由图5(b)可知，KI(此时KP=4.5、KD=0)可显著减小平台输出位移的稳态误差，KI增大到一定程度时可完全消除稳态误差，但KI会使平台输出位移出现超调。由图5(c)可知，随着KD(此时KP=4.5、KI=0.45)的增大，平台响应变慢，但平台输出位移的超调减小。

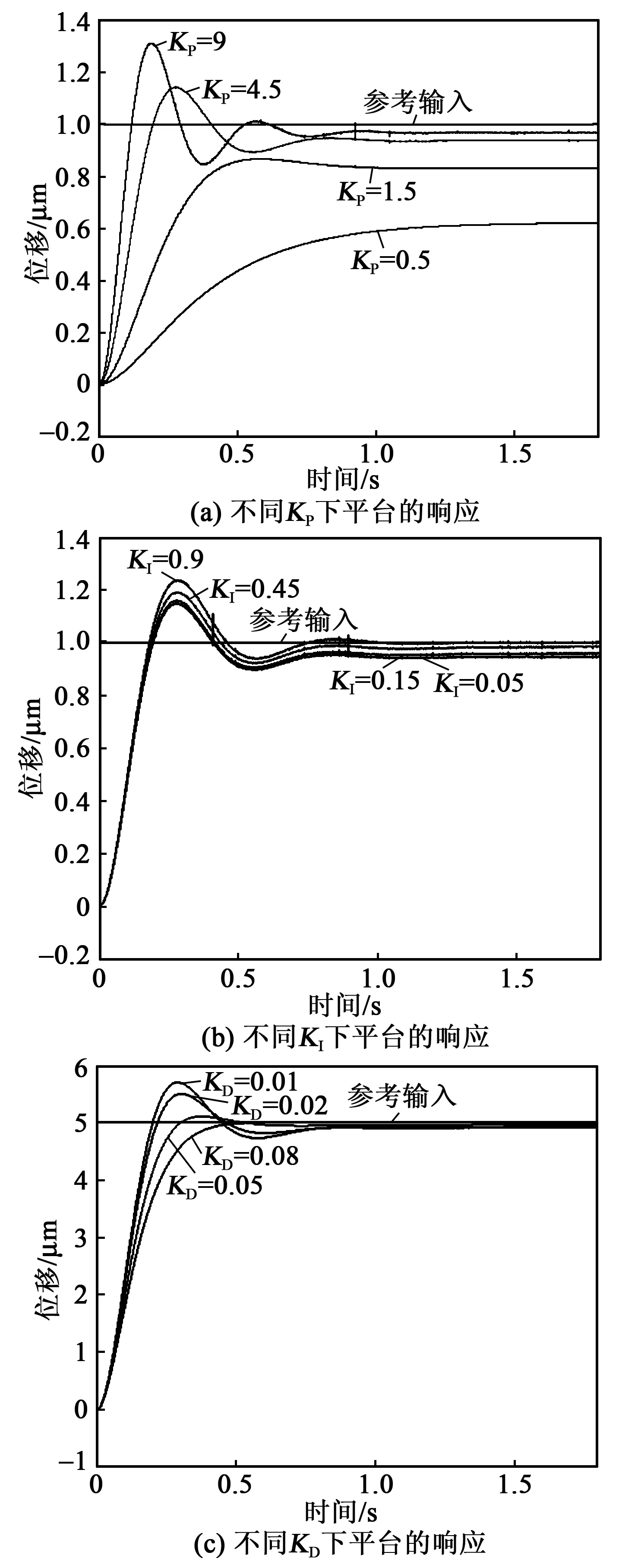
图5 KP、KI、KD对平台控制结果的影响

3 平台PID反馈控制实验验证

3.1 实验系统构成

图6为测量压电微动平台位移特性的实验系统，它由驱动电源、多功能卡、压电微动平台及电涡流位移传感器组成。其工作过程如下：由计算机发出相应的控制信号，该控制信号经多功能卡上的D/A转换器转换为连续的模拟电压，施加于驱动电源上，在电源所输出的驱动电压作用下，压电执行器伸长，推动微动平台使其产生微位移，该位移由电涡流位移传感器所测得，经多功能数据卡上的A/D转换器转换为数字信号，被输入计算机内。

图6 压电微动平台位移测量系统

由图6可知，电源输出电压的纹波为10 mV，线性度为0.1%，频带为0～2 kHz；电涡流位移传感器的测量范围为0.36～1.36 mm，非线性误差为0.4%，分辨率为0.1 μm。多功能数据卡上的A/D及D/A转换器的位数为16位，采样速度为100 kS/s。

3.2 阶跃响应

图7为采用钝化微分PID控制时压电微动平台的阶跃响应。由图可知，此时平台的响应时间较短(为0.3 s)，稳态误差为0，且无超调，可见所设计的钝化微分PID控制器可使平台具有良好的动态和稳态特性。

图7 钝化微分PID作用下微动平台的实际阶跃响应

3.3 三角波跟踪

给压电微动平台施加最大值为15.25 μm的变幅值三角波信号，由图8的测量结果可知，平台在未受控制的情况下，实际输出位移相对于目标位移的误差中线的变化范围为-0.7～1.2 μm；在钝化微分PID反馈控制的作用下，平台的实际输出位移相对于目标位移的误差中线的变化范围为-0.1～0.1 μm。因此，钝化微分PID反馈控制能较好地跟踪参考输入位移，使压电微动平台具有较小的定位误差。

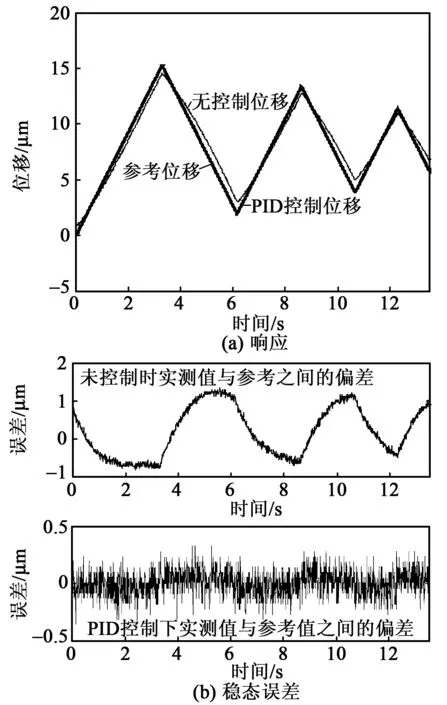
图8 钝化微分PID作用下微动平台的实际三角波输入

4 结束语

本文为避免压电微动平台在工作过程中受到干扰或冲击的影响，将低通滤波器引入常规PID控制中，设计出了平台的钝化微分PID控制器。采用MATLAB/simulink对设计的控制系统进行了仿真，结果表明，钝化PID控制器可有效消除干扰对平台输出位移的影响；KP增大时，平台响应加快且稳态误差减小，但太大时会出现超调；KI可消除平台输出位移的稳态误差，但太大时也会出现超调；KD增大时，平台响应变慢，但超调减小。实验验证了所设计的钝化微分PID控制的有效性，结果表明，平台达到5 μm阶跃目标的响应时间为0.3 s，无超调，且稳态误差为0；平台在跟踪最大值为15.25 μm的变幅值三角波时，定位误差中线由无控制时-0.7～1.2 μm减小为-0.1～0.1 μm。