A、B位空位比对PZT压电性能的影响
2019-02-22成炎炎杨国庆
成炎炎,李 坤,陈 森,杨国庆
(常州大学 材料科学与工程学院,江苏 常州 213164)
0 引言
具有钙钛矿结构的锆钛酸铅(PZT)陶瓷因其优异的压电效应而在压电换能器及传感器等电子元器件中得到了广泛应用[1-3]。PZT陶瓷的电学性能可以通过掺杂其他离子来进行优化,通过对比掺杂离子和目标离子价态的高低,可将其分为软性取代(施主掺杂)和硬性取代(受主掺杂)。如在PZT陶瓷中,La3+取代了处于A位的Pb2+,产生了A空位,Nb5+取代B位的Ti4+,产生了B空位[4-6]。高价离子取代使样品中出现阳离子空位,电畴运动变得更容易,矫顽场Ec下降,因此,在电场或应力作用下,材料性质变“软”。“软性离子”掺杂后,沿着电场方向取向的畴的数目增加,从而增加了剩余极化强度,压电效应增强。研究报告指出,在PZT陶瓷中掺杂Nb,能够抑制晶粒生长,提高陶瓷的致密度,同时,Nb2O5在PZT陶瓷的烧结过程中也发挥着重要作用[7]。但多年研究经验表明,Nb的掺杂量超过2%时,压电陶瓷的机电耦合系数(kp)随掺杂量的增加而迅速下降。另外,La和Nb的取代比例似乎对陶瓷压电性能有一定的影响。
本实验用La、Nb对PZT陶瓷进行掺杂,研究了A、B位的空位比及Nb含量对压电陶瓷性能的影响,并对实验结果进行了对比分析。
1 实验
1.1 PZT陶瓷配方的设计
PZT陶瓷为ABO3型钙钛矿结构,在ABO3型结构中,3种离子半径需要满足如下关系:
(1)
式中:rA、rB、rO分别为A、B和氧离子的半径;t=0.77~1.10为容差因子。由式(1)可以确定配方中各个离子的位置、空位和空位比。
本实验采用的配方为[(Pb0.93La0.07)1-α□α][(Zr1-y-zTiyNbz)1-β□β]O3(PLZTN)(r(Ti)/r(Zr)=39/61,z=0.02, 0.025, 0.03, 0.035,空位比α/β=1/1, 2/1, 3/1, 4/1, 5/1)。La3+取代了处于A位的Pb2+,产生了A空位,Nb5+取代B位的Ti4+,产生了B空位,根据电价平衡可以列出方程:
(2×0.93+3×0.07)(1-α)+[4(1-y-z)+
4y+5z](1-β)=2×3
(2)
简化式(2)可得:
2.07(1-α)+(4+z)(1-β)=6
(3)
根据Nb在B位的摩尔分数z的取值及α/β可算出不同配方中α、β的具体数值。y值可根据锆、钛摩尔比及z值确定,即
y/(1-y-z)=39/61
(4)
计算可得z=0.02,y=0.382 2;z=0.025,y=0.380 25;z=0.03,y=0.378 3;z=0.035,y=0.376 35。
1.2 PZT陶瓷样品的制备
采用分析纯的Pb3O4(99.8%),La2O3(99.8%),Nb2O5(99.9%),TiO2(99.8%),ZrO2(99.9%)作为原料。所有原料在120 ℃下干燥10 h后,按照配方中化学计量比准确进行称重。充分混合均匀后,将粉末在880 ℃下煅烧3 h,然后在球磨机中球磨4 h,随后加入质量分数为5%的聚乙烯醇作为粘结剂进行造粒并压制成厚约1.2 mm、直径∅16 mm的圆坯。将坯体550 ℃排胶后在1 270 ℃下烧结2 h,制备出PLZTN陶瓷样品。将z=0.02,α/β=1/1、2/1、3/1的样品编号为1、2、3;z=0.025,α/β=1/1、2/1、3/1、4/1、5/1的样品编号为4、5、6、7、8,依次类推。
1.3 样品的性能及表征
利用Rigaku D/max-2500/PC X线衍射(XRD)仪对陶瓷样品进行物相分析,通过Zeiss SupraTM55场发射扫描电子显微镜(FESEM)观察样品的显微组织形态。将样品抛光打磨后涂上银电极测量其电学性能,采用TH2818自动元件分析仪测量介电性能。将样品在常温下置于硅油中施加3 kV/mm的电场,极化3 min,用ZJ-6A型准静态d33测试仪测量陶瓷样品的压电应变常数d33。
2 实验结果与讨论
2.1 晶体结构分析
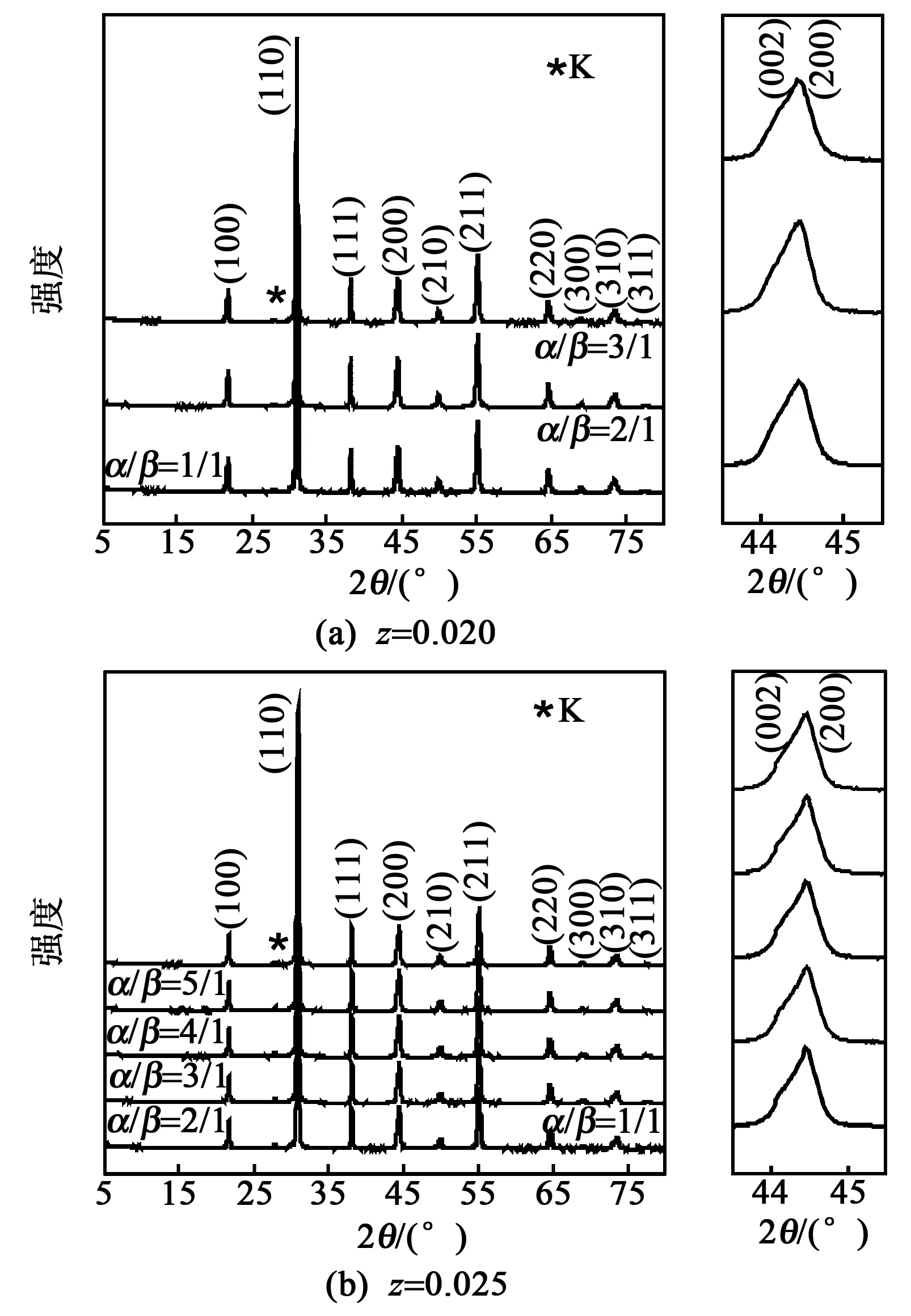
图1 PLZTN陶瓷的XRD图
图1为不同组分的PLZTN陶瓷的XRD图和2θ在43.5°~45.5°的放大图。由图1(a)可看出,陶瓷样品除{200}面族的衍射峰有轻微宽化迹象外,其余衍射峰都呈现对称、单一且尖锐的形状,无其他杂相,这说明不同配方的PLZTN陶瓷样品呈现纯的赝立方钙钛矿相结构,处于准同型相界(MPB)附近。另外,从放大的{200}衍射峰可以发现,空位比的变化对陶瓷的微观结构影响不大。由图1(b)也可得出相同的结论。对比图1(a)、(b)可见,在空位比相同的情况下,改变Nb掺杂量,各个衍射峰的角度和强度也未发现明显变化,说明Nb掺杂量对PLZTN陶瓷的微观结构无明显的影响。此外,根据布喇格定律可知,2θ在27°~29°范围内峰对应{110}面的K线,与杂相无关。
根据测得的XRD数据,表1为PLZTN陶瓷用MDI Jade 6.5软件计算得到的晶胞参数和密度。通过阿基米德排水法测得样品的体积密度。所有样品都具有很高的致密度(>97%),当z=0.02,α/β=2/1时,陶瓷样品的相对密度最大,达到了99.01%。
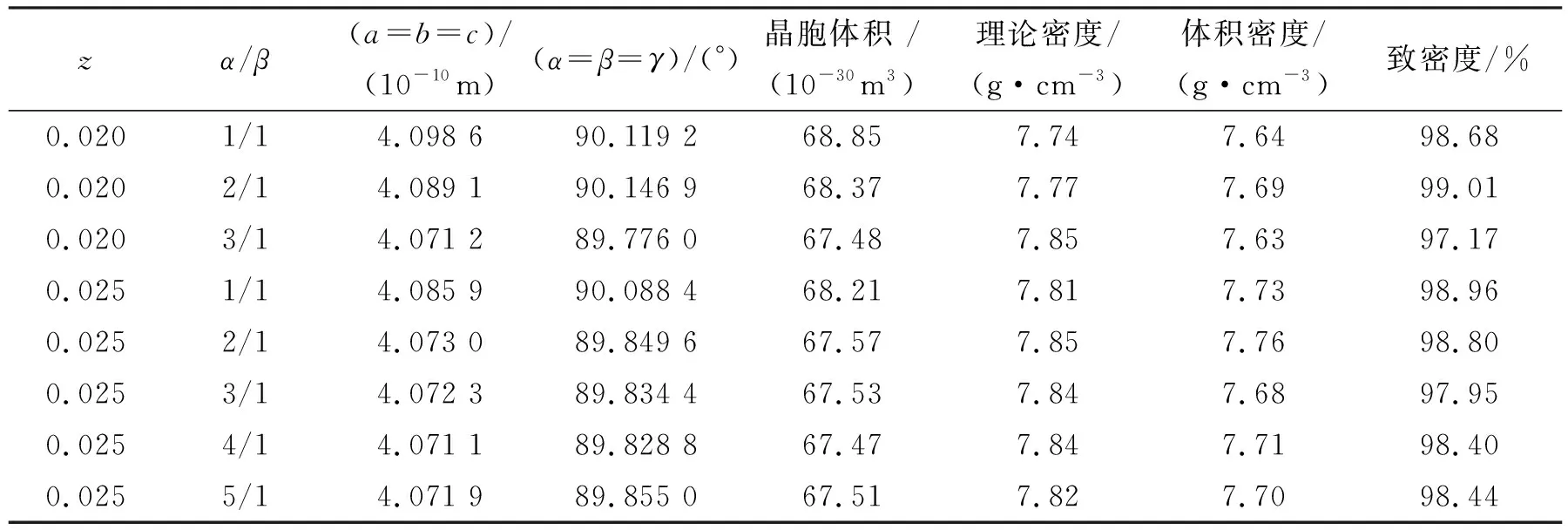
表1 不同组分的PLZTN陶瓷的晶胞参数和密度
2.2 显微结构分析
为分析PLZTN陶瓷的微观形貌,对组分1、2、3的陶瓷样品进行热腐蚀处理后,进行扫描电镜实验分析。图2为不同组分的样品表面、断面FESEM图。由图可见,组分1晶粒生长不完全,晶粒尺寸分布均匀性较差,断面显示的晶粒结合度也较低。组分2的陶瓷样品断裂方式为穿晶断裂,说明陶瓷结构良好,晶界牢固。组分3晶粒均匀性较好,但气孔较多,断面显示的结合性也较差。由此可以推断,组分2可能是压电性能较好的压电陶瓷配方。

图2 不同组分的[(Pb1-xLax)1-(□α][(Zr1-y-zTiyNbz)1-β□β]O3陶瓷的FESEM图
2.3 PZT陶瓷的介电性能
表2、3为不同组分的PLZTN陶瓷在频率1 kHz、室温下的介电常数和介电损耗。由表2可知,在Nb掺杂量相同的情况下,随着空位比的增大,介电常数总体呈现先增大后减小的趋势,这可能与晶粒增长、微观结构和致密化程度有关;在相同的空位比下,随着Nb掺杂量的增多,介电常数整体呈现增大的趋势。此外,
d33=2Q11εPs
(5)
式中:Q11为电致伸缩系数;ε为介电常数;Ps为自发极化强度。
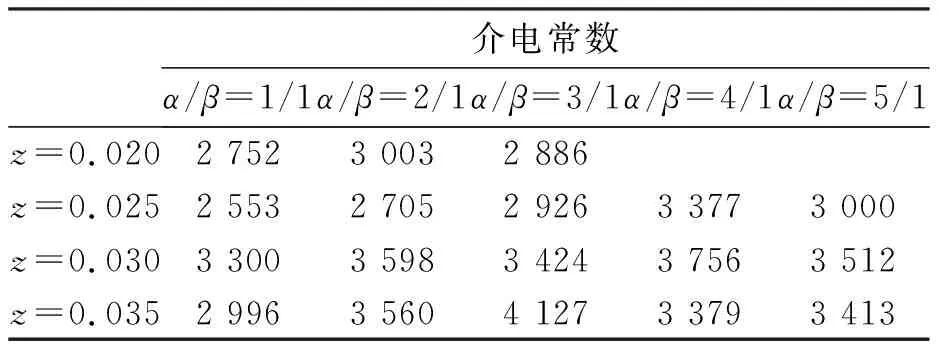
表2 陶瓷在1 kHz室温下的介电性能
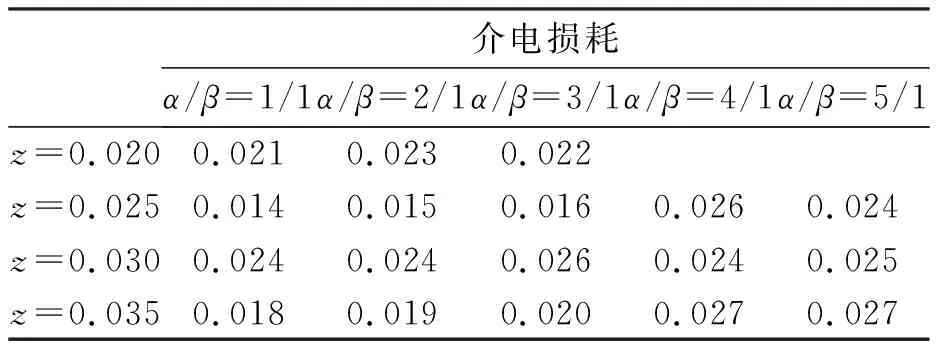
表3 陶瓷在1 kHz室温下的介电损耗
由式(5)可知[8-9],介电常数越大,越可能获得更大的d33,因此,z=0.025、α/β=3/1的陶瓷样品可能具有较好的压电性能。
由表3可看出,不同组分的PLZTN陶瓷的介电损耗都很小(<0.027),较低的介电损耗有利于陶瓷样品在高电场下的极化。z=0.025、α/β=1/1的陶瓷样品具有最低的室温介电损耗(为0.014)。总的来看,该系列的所有陶瓷样品具有较高的介电性能,较低的介电损耗,有利于电学性能的提高及陶瓷样品的极化。
图3为z=0.02时,不同α/β的陶瓷样品在1 kHz下的升温介电温谱。所有的陶瓷样品都只在180 ℃附近出现了一个介电峰,这对应于[(Pb0.93La0.07)1-a□α][(TiyZr1-y-zNbz)1-β□β]O3陶瓷宏观上在居里点TC/Tm(TC为居里温度,Tm为介电峰值对应的温度)处发生的从铁电相转变为顺电相的相变。此外,α/β对陶瓷样品的电学性能影响很大,图中不同的陶瓷样品不仅介电峰对应的温度略有不同,且介电峰值εm也相差很大。其中,α/β=1/1的陶瓷样品具有最好的介电性能,TC/Tm最高,εm最大,分别为178.6 ℃和13 679。
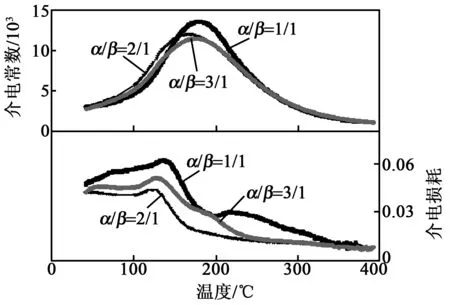
图3 不同空位比陶瓷样品在1 kHz下的升温介电温谱
对铁电材料高于TC/Tm区域的介电常数进行居里-外斯定律和指数定律拟合,是判断其为铁电体特征的有效方法。居里-外斯定律的公式为
ε=C/(T-T0)
(6)
式中:C为居里-外斯常数;T0为居里-外斯温度;T为温度。当C约为105量级时,说明在TC/Tm处发生的铁电-顺电相变是由位移型相变驱动的,而当C约为103量级时,说明在TC/Tm处发生的铁电-顺电相变是由有序-无序型相变驱动的。指数定律的公式为
1/ε-1/εm=(T-Tm)/C′
(7)
式中:γ为弥散系数;C′为常数。当γ=1时,说明是正常铁电体,而当γ=2时,则说明是弛豫铁电体。
图4、5分别为组分1的陶瓷样品在1 kHz时的居里-外斯定律拟合图和指数定率拟合图。居里-外斯定律的拟合结果为ε=1.79×105/(T-239),C在105量级表明组分1的陶瓷样品在TC/Tm处发生的铁电-顺电相变是由位移型相变驱动的。另外,可以发现居里-外斯定律在TC/Tm以上一段温度是偏离10 000/ε-T曲线的,根据偏离程度ΔTm=Tcw-Tm=100.4 ℃(Tcw为介电响应开始偏离居里-外斯定律的温度)。根据指数定率拟合的结果可得γ=2.125,与指数定律并不相符。[(Pb0.93La0.07)1-α□α][(TiyZr1-y-zNbz)1-β□β]O3陶瓷这种复杂的介电行为,可能是由于该陶瓷配方成分复杂,元素种类较多,且γ较接近2,具有弛豫铁电体的特征。
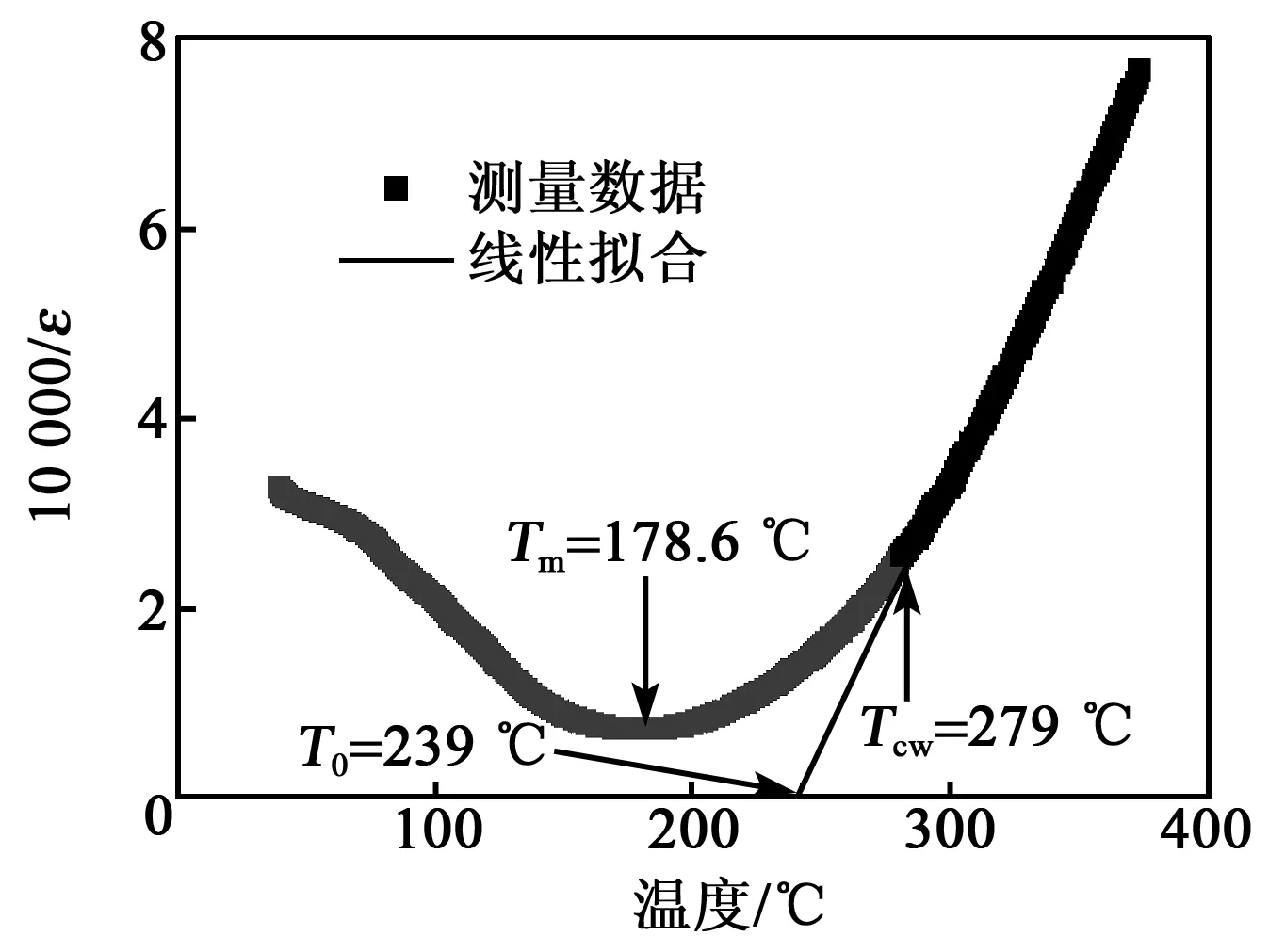
图4 组分1的陶瓷样品在1 kHz时的居里-外斯定律拟合图
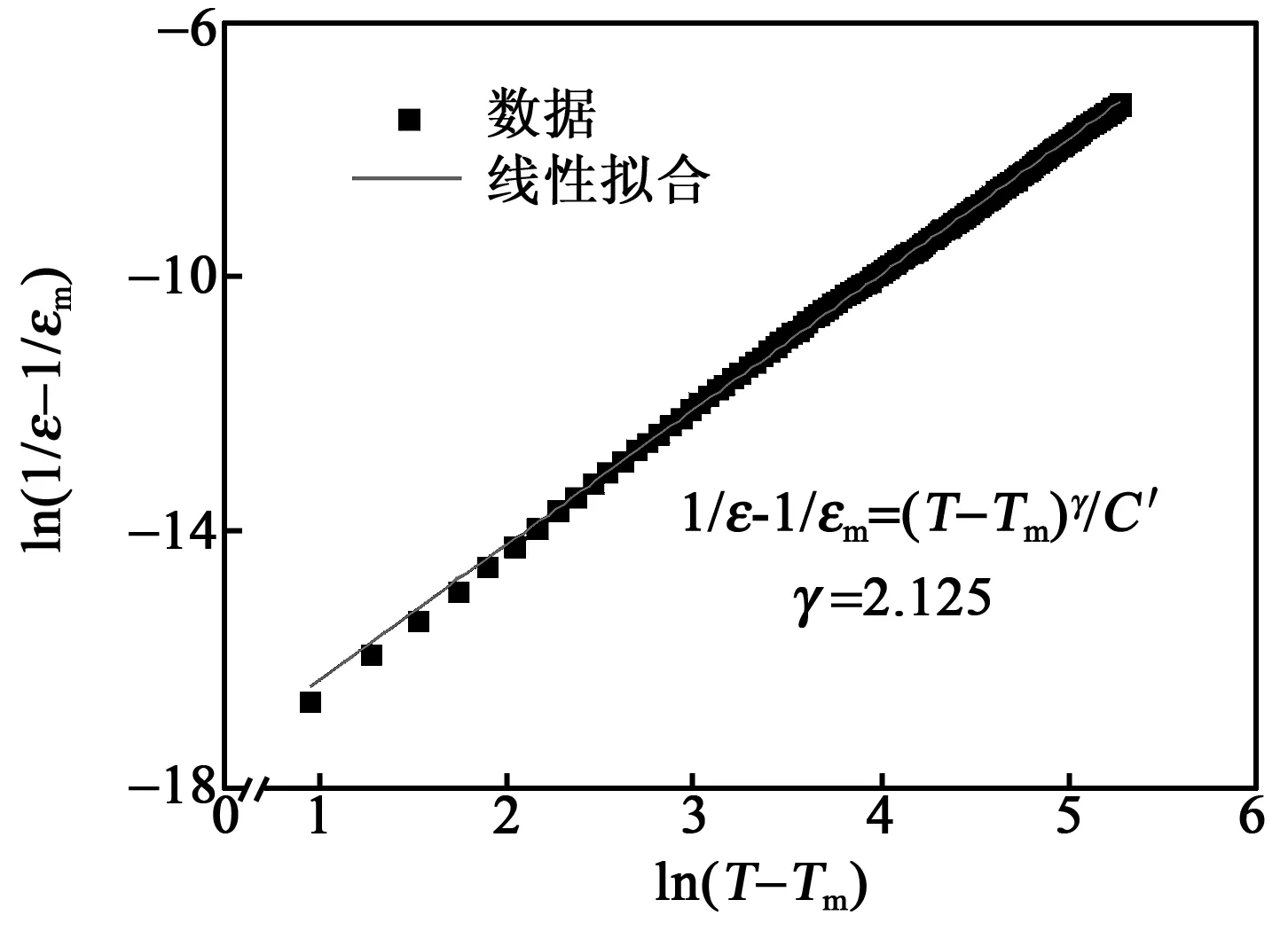
图5 组分1的陶瓷样品在1 kHz时的指数定律拟合图
2.4 PZT陶瓷的压电性能
图6为3 kV/mm电场下极化后的组分2的陶瓷样品的阻抗、相位角与频率的关系图。图中看不到明显的杂峰或串扰,且图中所得相位角θ=89.92°,接近90°,说明其已经充分极化[10]。
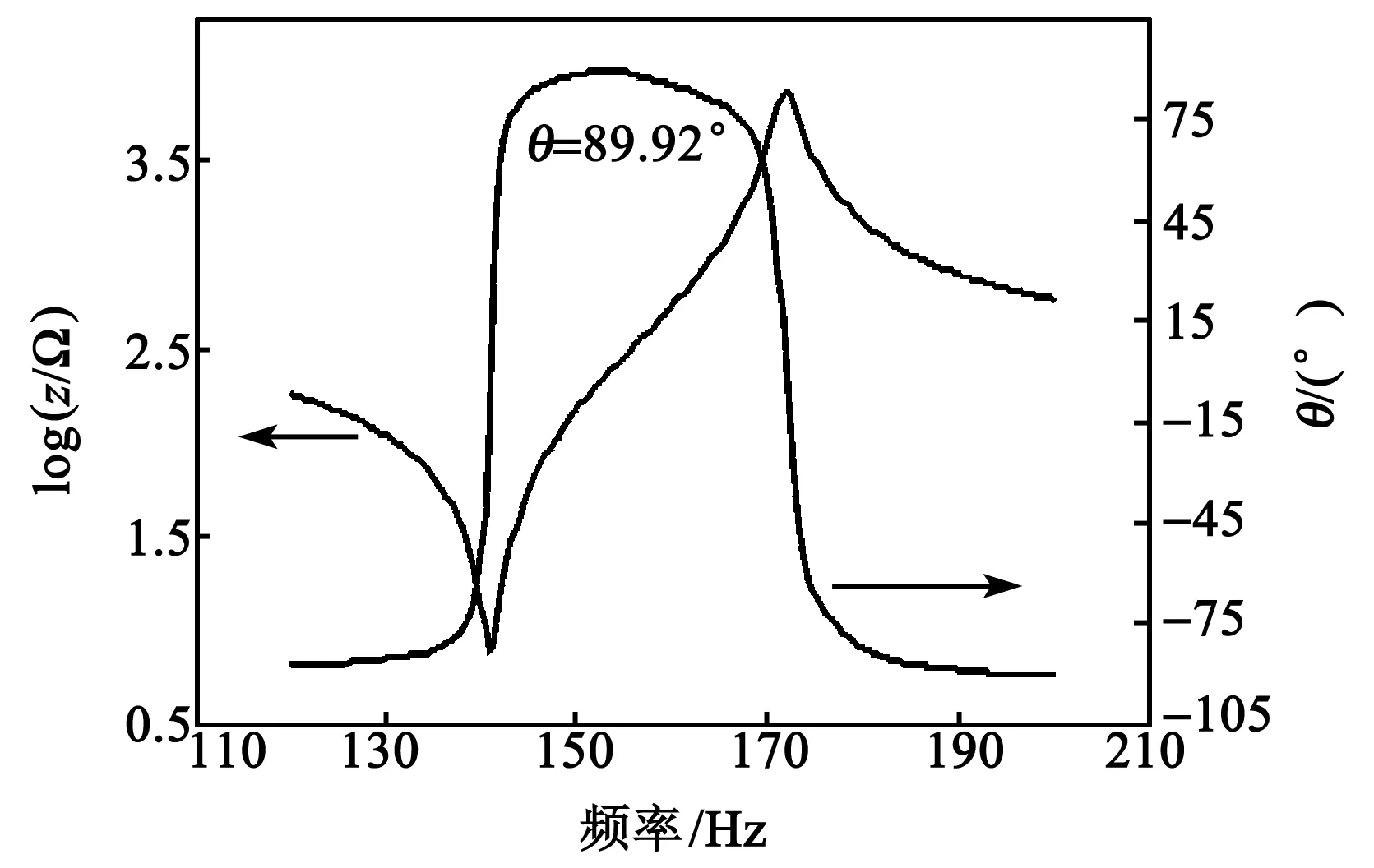
图6 3 kV/mm极化的组分2的陶瓷的阻抗、相位角与频率的关系
d33和机电耦合系数是表征陶瓷压电性能的两个最重要的参数。图7、8分别为不同组分的[(Pb0.93La0.07)1-α□α][(TiyZr1-y-zNbz)1-β□β]O3陶瓷的d33和平面机电耦合系数kp随α/β的变化关系图。
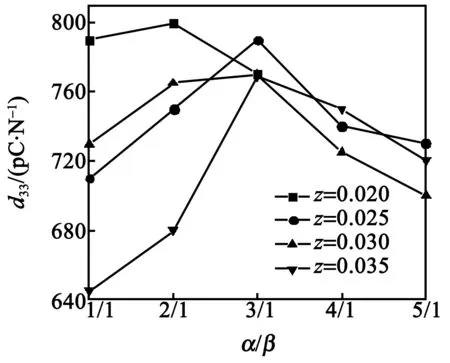
图7 不同组分陶瓷样品的d33与α/β的关系
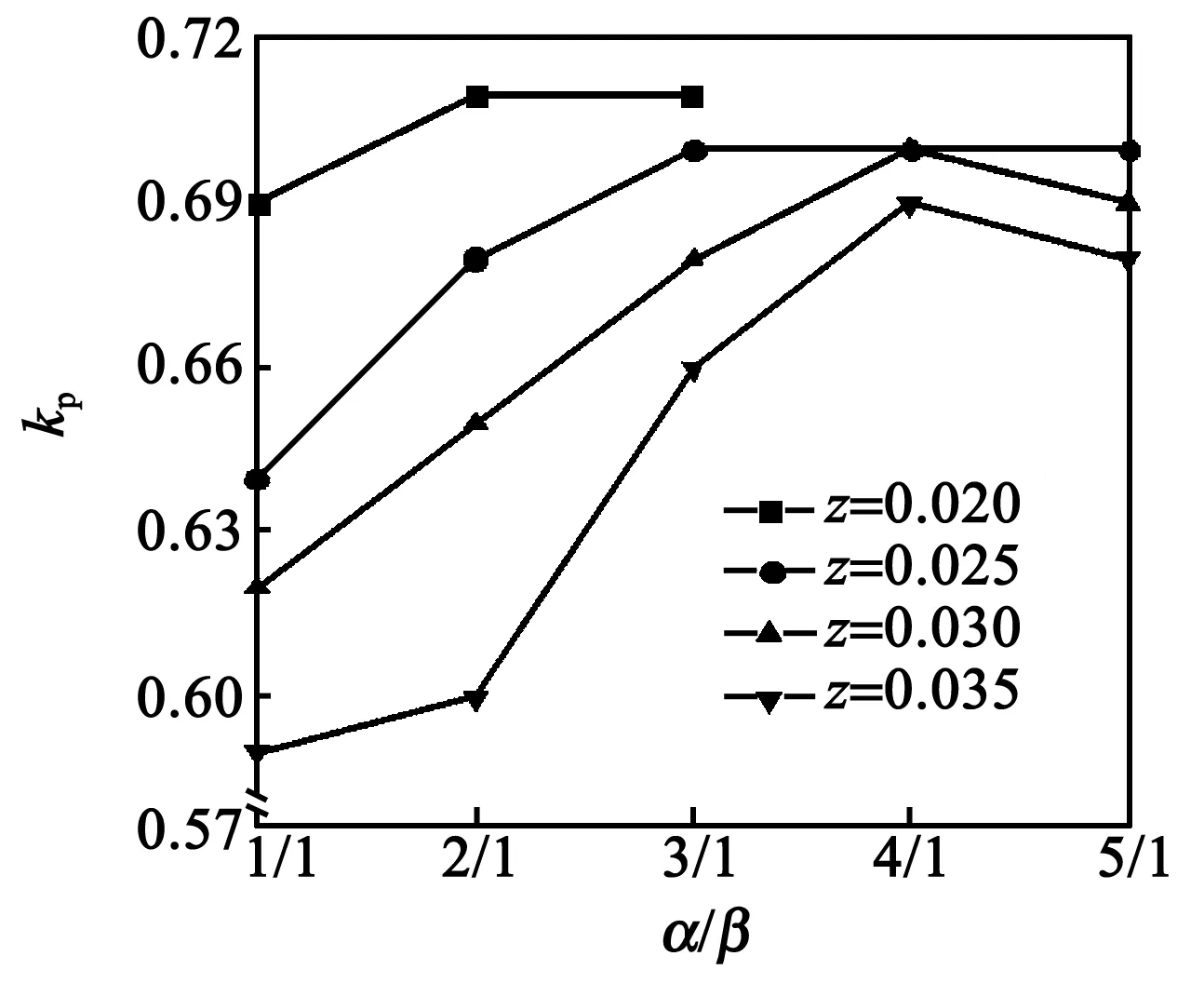
图8 不同组分陶瓷样品的kp与α/β的关系
由图8、9可看出,在Nb掺杂量相同的情况下,随着α/β的增大,d33和kp都呈现出一种先增大后减小的趋势。当z=0.02,α/β=2/1时,d33达到最大值(为800 pC/N);随着α/β的继续增加,d33反而下降了,这可能是由于过高的α/β使晶相偏离准同型相界,导致d33不断地减小。α/β=1/1、2/1时,随着z的增加,d33和kp都呈现出下降的趋势,说明过量的Nb5+不利于陶瓷压电性能的提高。
2.5 PZT陶瓷的热稳定性
由于在高温环境中使用的压电陶瓷会发生退极化,并使其压电性能发生退化,因此,对于压电材料,探究其热稳定性和温度使用范围也十分重要[11]。我们将3 kV/mm电场极化后的组分2的陶瓷样品在不同温度Ta下退火5 min后在室温下测量,得到了d33和kp随温度的变化关系,如图9所示。由图可看出,陶瓷的d33和kp值在低温时基本上没有下降,当温度为110 ℃时,d33下降了约9.1 %,陶瓷样品的d33=727 pC/N,kp=65 %。温度升高到约125 ℃时,由于发生的铁电-顺电相变,d33、kp出现了陡然下降,表明[(Pb1-xLax)1-α□α][(TiyZr1-y-zNbz)1-β□β]O3陶瓷具有良好的热稳定性。
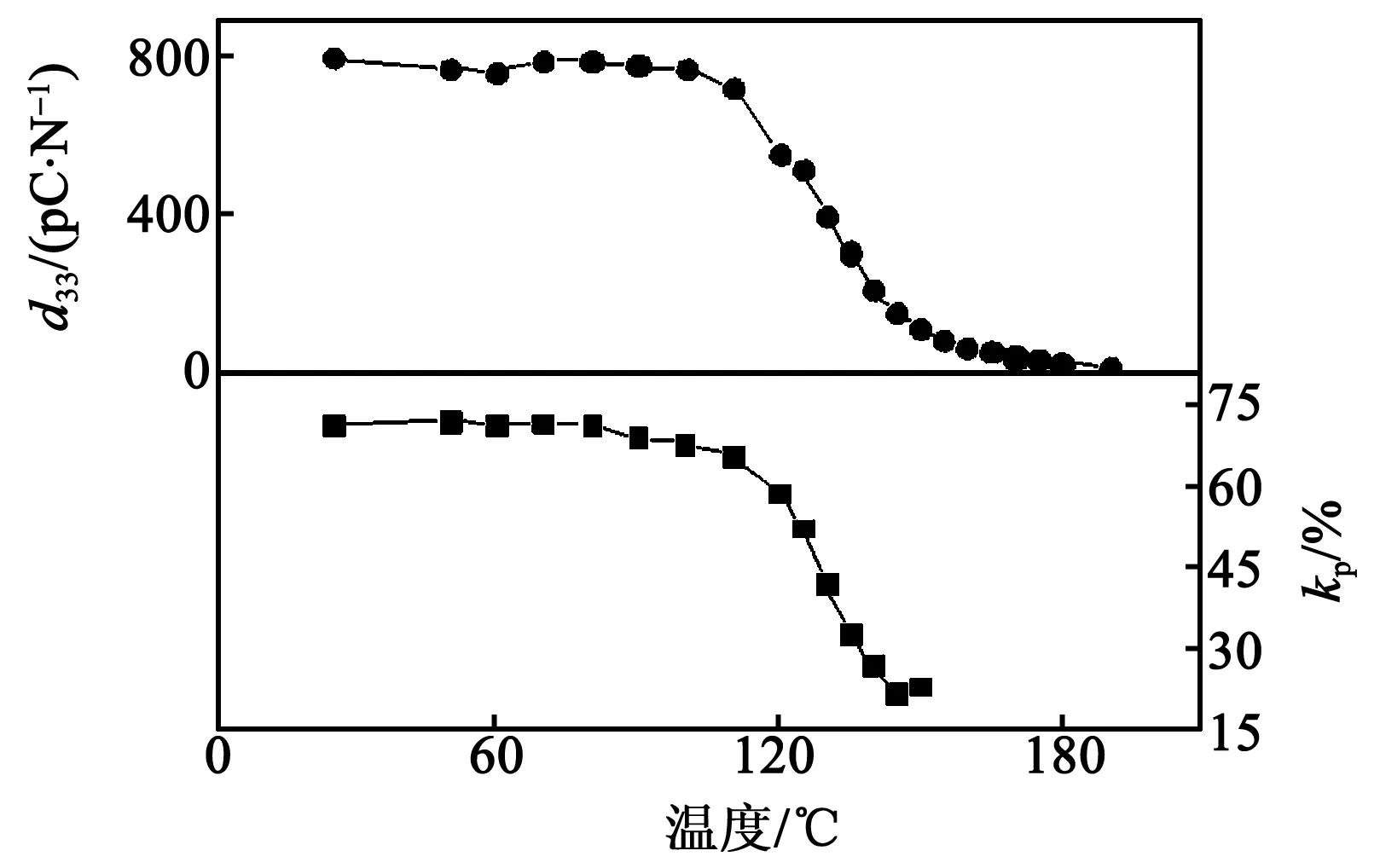
图9 组分2的陶瓷样品的d33和kp随温度的变化
2.6 压电薄片振子和双晶
用组分2的陶瓷配方制作0.22mm×7.8mm×45mm的压电片,其横向机电耦合系数k31可达0.46。该陶瓷片组装的双晶片,在180 V电压驱动下其悬臂梁结构的自由端零位移推力为32 g,空载位移量为0.8 mm。该材料是纺织经编压电贾卡制造的较理想材料。图10为压电陶瓷双晶片的示意图和实物图。图中,l为双晶片的悬臂长度。
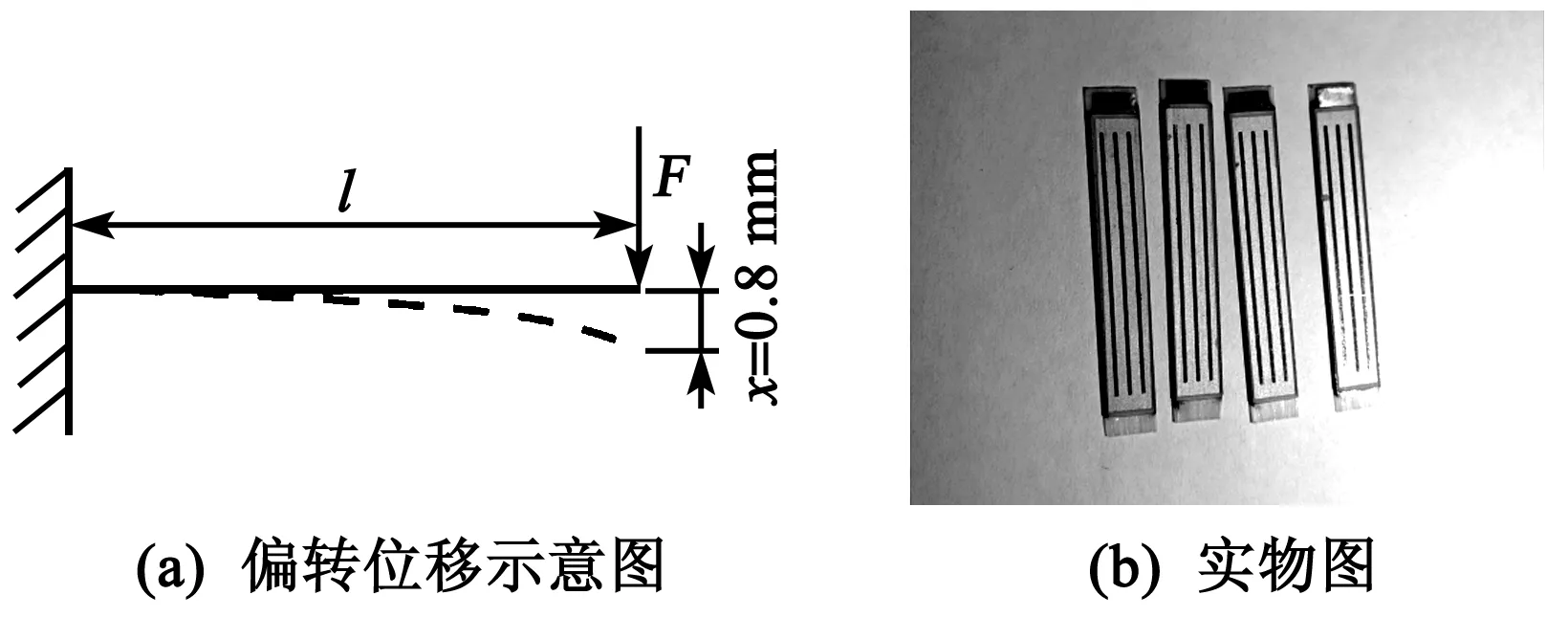
图10 双晶片示意图与实物图
3 结论
1) 采用传统氧化物混合的方法制备出钙钛矿结构的[(Pb0.93La0.07)1-α□α][(TiyZr1-y-zNbz)1-β□β]O3陶瓷,所有陶瓷样品的致密度都很高,最高达到了99.01%。
2) 当Nb掺杂量z=0.02,空位比α/β=2/1时,陶瓷样品的压电性能最佳:压电应变常数d33=800 pC/N,平面机电耦合系数kp=71.85%,且具有良好的热稳定性。
