特殊环境下非接触式定位系统的设计
2019-02-22张泽华张丕状王建国
张泽华,张丕状,王建国
(1. 中北大学 信息与通信工程学院,山西 太原 030051 2.太原工业学院 电子工程系,山西 太原 030051)
0 引 言
在现代工业中,有许多情况需要对狭小、光线昏暗的封闭空间的目标进行非接触式定位,传统的光栅定位在这种环境下受到很大影响,比如:因为空间狭小导致光栅尺无法使用; 普通光栅板成像容易受到外界干扰等. 本文在传统光栅尺定位以及普通光栅板定位的基础上,提出了一种基于多狭缝光栅板的非接触式定位系统的设计. 本文采用多狭缝光栅板成像,光通过光栅狭缝透射到传感器上得到波形数据,波形数据包含光在传感器上落点位置分布以及光强分布,根据波形匹配实现对目标的定位. 相比传统光栅尺和光栅板的定位系统,光栅选用特殊多缝光栅板,且不需要聚光透镜,测量范围变大,成本更低,系统抗干扰能力更强.
1 非接触式定位系统的设计
1.1 传统光栅定位系统的分析与比较
由于要在光线昏暗,空间狭小的环境实现定位,传统的光栅尺已经不再适用. 因此,选用光栅板实现定位更适用于这种特殊环境.
传统光栅板成像可分为反射成像和透射成像.
对于反射成像系统,如果系统中使用普通光学透镜,则要求目标所在面要与传感器接收面平行,否则按照原来的数学模型会得到错误的目标二维坐标位置(如果目标所在面与传感器接收面不平行,实际的法线会向数学模型的法线两侧偏移,这样按照数学模型计算出来的数据就和实际不相符),甚至反射光线会超出传感器的测量范围[1,2]. 如果用聚光透镜(凸透镜)作为光学元件,可以解决目标所在面要与传感器接收面平行的问题,但透镜成本太高. 本文的算法不依赖光的反射原理,而是通过立体几何计算的,目标所在面与传感器接收面平行与否对系统没有影响[3,4].
对于透射成像系统,普通光栅板成像时,目标在相近的两个位置上通过普通光栅在传感器上成的图像之间相似性很高,这样会导致后续计算中的误差较大,也就是说,使用普通光栅会使系统本身误差较大. 本文采用的光栅为多缝光栅,相邻狭缝间距不等,且相邻间距之间比值不等,这样可以保证目标在某一位置通过光栅在传感器上得到的数据具有独特性,不会出现目标在两个不同位置通过光栅在传感器上所得数据之间的高相似性,从而保证了系统本身的准确性[5,6]. 例如,间距分别为1.1 mm,1.2 mm,1.3 mm,1.4 mm 的4条平行狭缝构成的光栅,在测量范围内,分别在任意不同的两点p1,p2处的目标通过光栅在线阵传感器上可得到两组数据A1,A2,其中目标在传感器上的落点所在位置在数据中表示为1,其余表示为0,A1与A2做内积的结果最大为1,因此A1与A2之间相似性很低[7,8].
1.2 系统外部模型构建
系统外部构造包括:目标、光栅板、传感器. 目标在y轴、z轴两个方向上运动,通过光栅将光信号传递到线阵图像传感器上,光栅的多个狭缝使得传感器上会得到多个对应落点,系统外部模型如图 1 所示.

图 1 系统外部模型Fig.1 System external model
1.3 系统算法流程设计
母板:设目标在点p处经过光栅,在线阵图像传感器上得到一组投影数据向量,这组数据就是母板. 母板不是真实存在的,而是通过算法计算出来的参照物,母板的数据长度和传感器输出数据的长度一样,母板的作用是产生子板.
子板:通过对母板进行矩阵的伸缩、平移变换得到新的数据,这组新的数据就是母板产生的子板,不同幅度的伸缩、平移变换可以得到不同的子板. 子板是通过母板这个参照物变换得到的,目标通过传感器得到的数据会和子板中的某一个或几个有很强的相关性[9,10].
不同子板对应目标所在不同位置,该位置由母板对应的目标位置和子板的伸缩、平移程度决定.
构建母板,在母板的基础上构建子板,待测目标通过线阵图像传感器得到数据,对该数据进行采集和图像处理[11,12]得到目标数据,使其与子板进行模板匹配,得到与目标数据最匹配的子板,与子板相对应的目标位置就是待测目标所在位置,系统算法流程如图 2 所示.
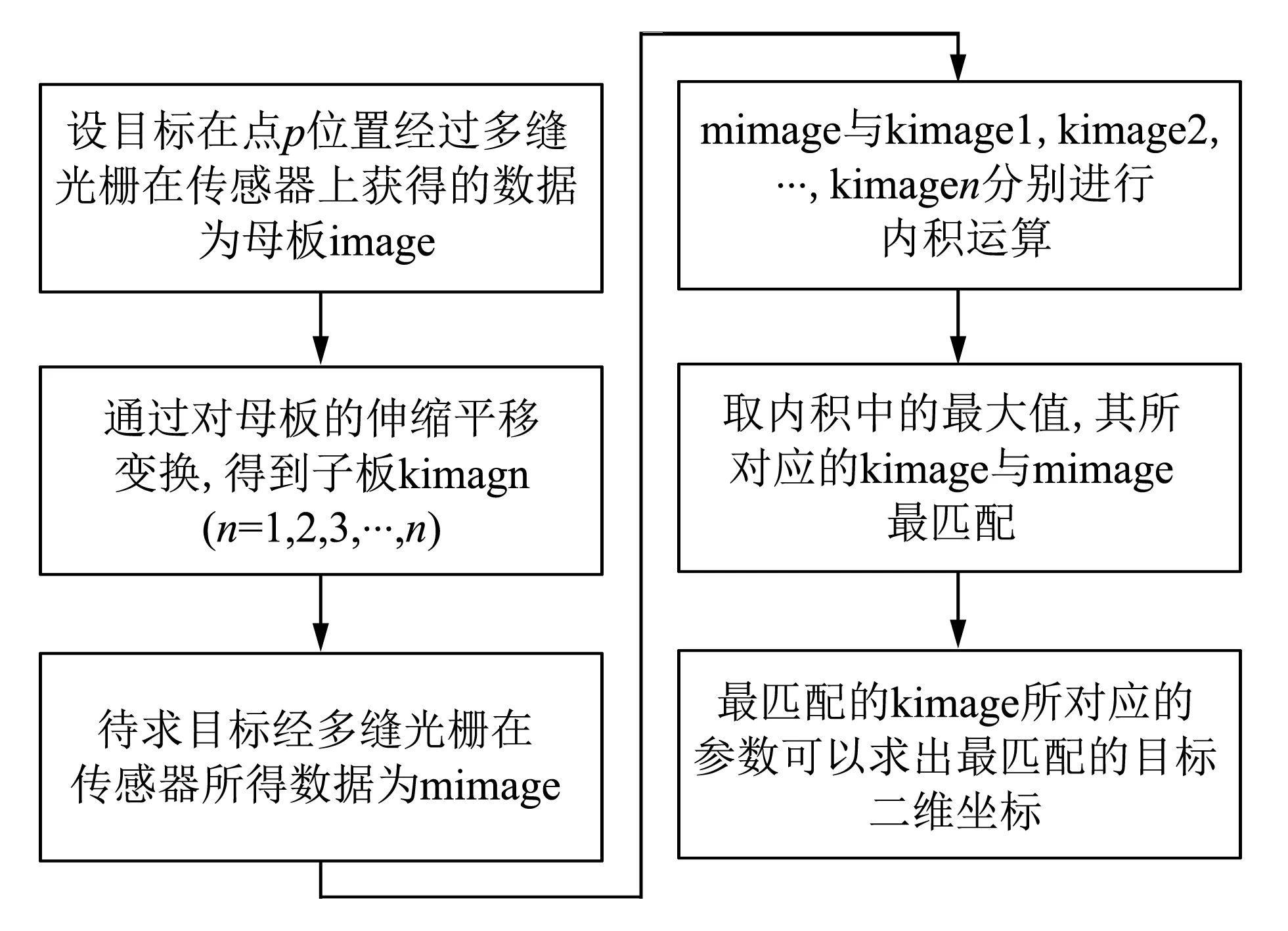
图 2 系统算法流程图Fig.2 System algorithm flow chart
2 数学模型构建与MATLAB仿真
2.1 数学模型构建
根据系统设计,提出数学模型,模型中光栅有两组狭缝,之后再延伸到多狭缝. 空间点p为目标所在位置,两条直线l1,l2为两条光栅狭缝所在直线,直线l3为线阵传感器上光敏元件组所在直线,ylm,ylM是目标通过光栅不同狭缝落在投影面上的坐标值,d为光栅所在面与投影面之间的距离[13]. 本次设计针对目标二维坐标(y0,z0),所以目标在x轴的位置不用考虑. 模型为:
已知:空间点p(y0,z0),一平面上有两条直线,l1∶y=m;l2∶y=M,另一平面上有一条直线,l3∶x=w,过点p分别和两条直线构成两个平面s1,s2.
得平面方程
s1∶(d-z0)(y-y0)=(m-y0)(z-z0),(1)
s2∶(d-z0)(y-y0)=(M-y0)(z-z0).(2)
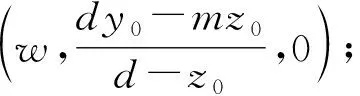
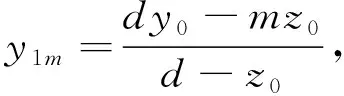

根据式(3)、式(4),可以得到目标在点p位置通过光栅落在传感器上的位置.
对式(3)求全微分,有
(5)
式中:Δy1是目标移动导致投影面上的落点位置的变化量; Δy0, Δz0分别是光点在y方向和z方向的变化量.
由式(5)可知:已知目标在某一定点p处时投影在传感器上的数据,通过对这组数据进行矩阵平移、伸缩变换,可以得到目标在不同位置上投影[14]到传感器上的数据.
2.1.1 母板构建
算法中的实现方式是:创建一个1*2000的全零向量并赋值给母板,作为母板的初始数据(因为没有光落到传感器上的时候,传感器输出数据全为零),通过公式可以计算出目标在传感器上的落点位置,落点的光照强度最强,因为实际实验中光栅狭缝有一定的宽度,所以在落点左右两侧应该各有一段光照强度递减的地带,将这些落点位置的输出数据设置为150,两侧数据递减,直到为零. 由此可以得到母板的数据,记为image.
2.1.2 子板构建
数学原理:向量的伸缩、平移变换可以通过向量的乘积来实现. 构建一个2000*2000的单位矩阵A,对A进行不同幅度的伸缩和平移变换后得到不同的变换矩阵A1,A2,A3,…,An(n=1,2,3,…,n),image与An的乘积的结果就是image进行伸缩和平移变换后的向量,也就是子板kimagen.
算法中的实现方式:子板是在母板的基础上实现的,在图二的算法中,只需要将点p改变,就能得到相应的子板,点p只能变成在测量范围内的点. 通过循环改变p的坐标,生成p1,p2,p3,…,pn,求出相应的子板kimage1, kimage2, kimage3,…,kimagen.
2.1.3 通过内积找到最匹配的数据
数学原理:根据正交原理,两个向量如果正交,它们的内积为零,两个正交的向量相关性最低. 目标通过正交光栅在线阵图像传感器上得到一组投影数据mimage,mimage分别与kimage1, kimage2, kimage3,…,kimagen进行内积运算,找出数值最大的内积,最大内积相对应的子板kimagen和mimage相关性最高.
算法中的实现方式:通过最大的内积[15]找到对应的kimagen,从而得到对应的pn,pn即为与目标位置最近似的点.
2.2 MATLAB仿真
根据数学模型,构建出多狭缝光栅,本次仿真的狭缝所在直线分别是y=-11 mm,y=-8.6 mm,y=-6.3 mm,y=-4.1 mm,y=-2.1 mm,y=0,y=2.1 mm,y=4.1 mm,y=6.3 mm,y=8.6 mm,y=11 mm.
图 3 为数学模型的仿真,目标在点(0,100)处通过光栅在传感器上的数据中,光照强度最大的几个点就是目标通过不同狭缝在传感器上的落点,落点两侧光照强度递减.

图 3 数学模型仿真Fig.3 Mathematical model simulation
表 1 为仿真测试结果,通过算法得到的目标位置与目标实际位置一致.

表 1 实际位置与测试位置对比
图 4 为加入高斯噪声后目标在点(0,100)处通过光栅在传感器上的数据.
表 2 为加入高斯噪声后的仿真测试结果,通过算法得到的目标位置与目标实际位置一致,由此可以看出系统在抗噪方面效果显著.

表 2 加噪声后实际位置与测试位置对比
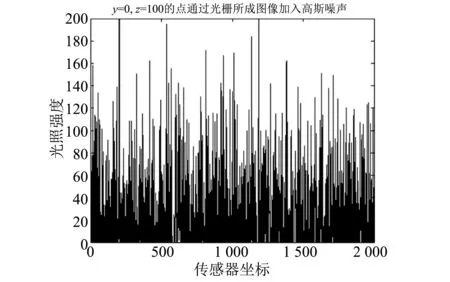
图 4 加入高斯噪声Fig.4 Adding Gaussian noise
3 结 论
本文阐述了一种特殊环境下非接触式定位系统设计的基本原理,并对此方法进行了仿真与分析,验证了此方法在理论上的可行性,但还需要进行实际测量来确定此方法的精度以及适用范围.
