基于Petri网模型的零件出库系统工作流并行结构分析

梁 迪, 刘 跃, 白蒙蒙

(沈阳大学 机械工程学院, 辽宁 沈阳 110044)

算法和模型的提出是为了解决多元化的复杂问题,例如用Dijkstra算法解决最优路径选择问题[1];田口方法则被运用到质量控制中[2];工作流模型以其快速过程建模、便于优化分析和自动化的特点,在各大企业中被广泛应用;应用工作流模型对业务流程建模有助于企业科学的管理,具有重要意义.

目前, 国内外众多学者对基于Petri网的工作流的业务流程模型进行研究. van der Aalst[3]最先将Petri网运用到工作流的业务流程建模中, 并规定了可以运用Petri网构建的工作流模型, 单继城等[4]运用着色Petri网的概念, 采用模块聚合的方式建立了混合工作流的CPN模型对流程的正确性进行了分析, 笪建等[5]结合进程代数对业务过程进行研究. 本文在研究了工作流基本结构的基础上, 运用Petri网对案例建模, 分析了该工作流模型任务间的结构关系, 从而列出关联矩阵, 并用MATLAB进行求解, 从运行时间的角度出发, 综合求解的结果, 对原有的工作流模型进行重新划分, 优化原有的Petri网模型, 最终降低系统内部运行时间, 提升系统处理效率.

1 工作流、Petri网概述

1.1 工作流的相关概念

工作流是计算机化的模型,模型是所有的工作参数的集合,这些参数又包含了每个步骤的内容、操作顺序、执行条件、数据流的建立及彼此之间的关联.工作流模型同传统模型的概念在某种程度上是一致的,都是用符号、文字、关系式、图表等形式表达的模型.模型通常包含必要且得到承认的通用规则,拥有准确描述形式.一个完整的工作流模型,应该具备定义流程所必需的特征和要素.评判工作流的性能有强大的描述能力、形象直观、最小化、形式化4个要素.工作流模型能够将一个工作细分成若干具有规范的、良好的任务和角色,并按照规定的标准实施,进而实现有效的监督.

1.2 Petri网的相关概念

Petri网是表示离散并行系统的图形语言.作为图形语言,Petri网拥有和流程程序图相似的直观化功能,并根据托肯(token)表示出动态的系统行为.作为数学工具,通过状态方程、关联矩阵及P/T不变量可用来描述系统的结构特征.

Petri网是有向图,是由N={P,T,F}组成的三元组表示的网图(Net),其中P={P0,P1,…,Pm}表示有限的库所集合,T={T0,T1,…,Tn}表示有限的变迁集合,F是库所与变迁节点间有限的有向弧集合[6].Petri网则满足以下条件:

(1)P×T≠∅;

(2)P∩T=∅;

(3)F⊆(P×T)∪(T×P);

(4) dom(F)∪cod(F)=P∪T,

dom(F)={x∈P∪T丨∃y∈P∪T:(x,y)∈F},

cod(F)={x∈P∪T丨y=∈P∪T:(y,x)∈F}.

P和T是Petri网中的基本元素,是2个不相交的集合,其中P元素为库所,T元素为变迁,F是网中的流关系,即连接P与T的有向弧[7].

1.3 工作流与Petri网的关系

工作流是由多个伴随着执行条件的任务组成,其特点为图形化与流程化.Petri网则可用图形表示流程,因此这两者的特点不谋而合.Petri网可以更直观地表现出工作流程逻辑,且能对流程性能进行分析.工作流业务过程中的任务、条件、过程和触发等可以分别映射为 Petri网中的元素库所P、变迁T.其中任务代替变迁,条件用库所代替、过程为有向弧F.因此工作流可用Petri网表示的条件是:

(1) 工作流Petri网模型中有且只有1个开始库所和1个终止库所;

(2) 模型中没有独立节点,所有的任务和条件都与流程相关;

(3) 所有库所的标识随着流程的结束转变为最终标识,流程结束后只存在1个标识.

2 结构类型与并行结构优化分析

工作流中定义了4种基本结构类型,并行优化后的图形结果如表1所示.

3 工作流Petri网建模过程

建模的基本过程如下所示:

(1) 分析案例的发生条件;

(2) 分析任务间的关系及结构类型;

(3) 将工作流模型分解成若干份;

(4) 根据分解后的部分建立模型,库所代表条件,变迁代表任务;

(5) 初步分析模型,并将其进行完善;

(6) 将完善后的模型进行优化分析,最终得到期望的工作流模型.

本文以零件出库系统的流程为案例,对其工作流程进行分析,如图1所示.

图1 零件出库系统流程图

根据并行结构优化算法, 运用Petri网理论, 构建了该工作流的Petri网模型, 如图2所示.

她经常凝望自己的脸。在酒店或者餐厅洗手间的镜子里，在商店的试衣镜里，在家里梳洗台的镜子里，见到不同时刻的面容，疲惫的，隐忍的，衰竭的，意兴阑珊的。她想认清和确定自我的来源和实质。而那个新的自我，是脸颊上膨胀出两团胭脂红晕的女子。年少时，做爱之后脸颊就会变得这样红，微醺而烂熟的云霞般绚烂沉醉的红晕。她害怕失去这种敏感而独特的身体反应。

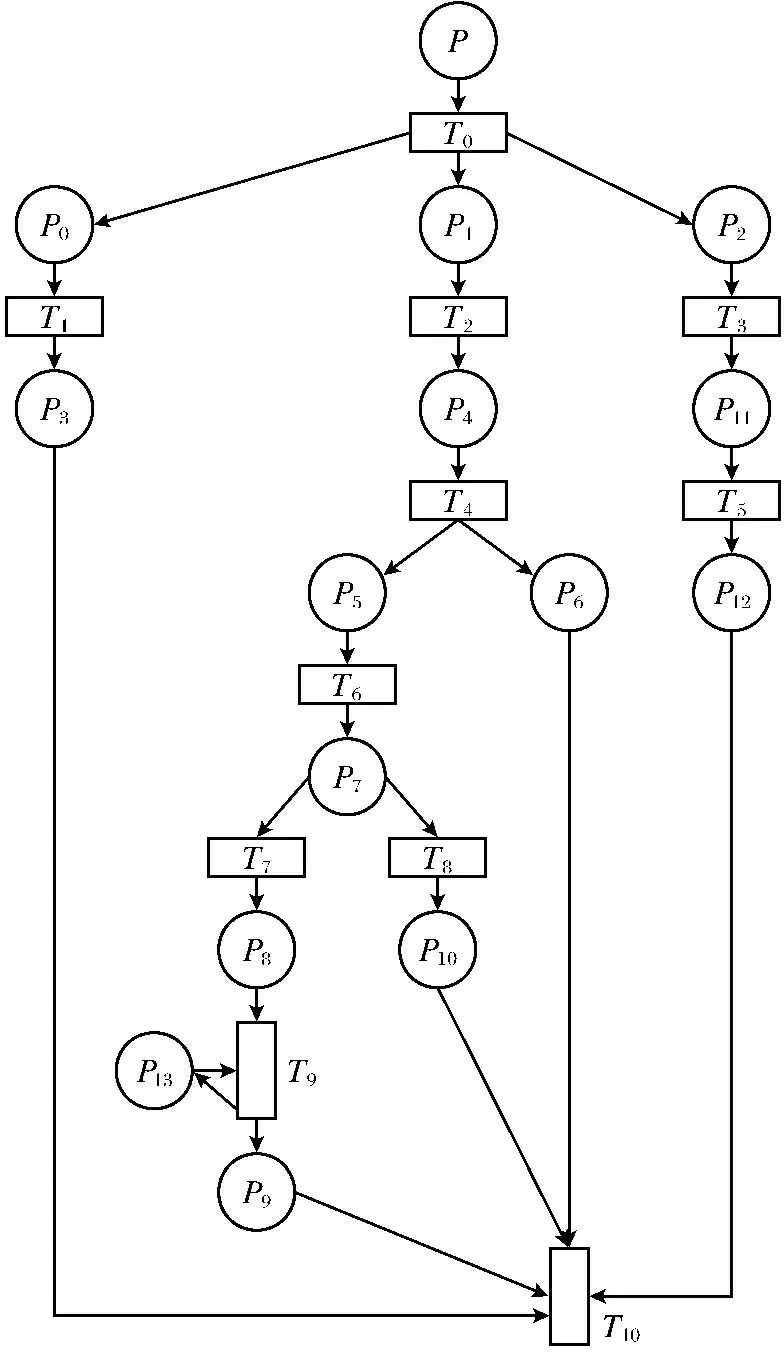
图2零件出库系统的Petri网模型图

Fig.2 The of Petri net model of part delivery system

图2中零件出库系统Petri网的流程元素如表2所示.

表2 Petri网模型与流程的对应关系

从图2的模型中可以看出,T2与T4,T3与T5属于顺序结构,并行化应采用流水线技术.整个模型是查询生产信息、查询缴费信息、查询需求和库存情况3部分组成的并行结构,采用空间并行法对其并行化.

查询缴费信息时出现的选择冲突,运用流水线技术对其并行化.因此,加入了库所P14与P15,库所T7、P15、T8、P14变成了控制回路.当出现刷卡缴费时,下一人必须选择现金缴费,这样流程才能继续进行,如果下一人选择刷卡缴费,则需等待上一人结束后才能进行缴费.

4 运算与分析

根据图2的Petri网模型得到关联矩阵D.

通过在MATLAB软件上进行运算分析,得到初始标识M0={1,0,0,0,0,0,0,0,0,0,0,0,0},库所不变量分别为

库所不变量X1、X2、X3对应的子网1={X1,X3}和子网2={X2,X3}满足并行和划分条件.经过划分,得到了3个并行进程,即查询生产情况、进入缴费系统缴费的进程、查询订单信息及库存情况.对并行算法处理后的系统运用P-不变量进行时间分析,结果如表3所示.

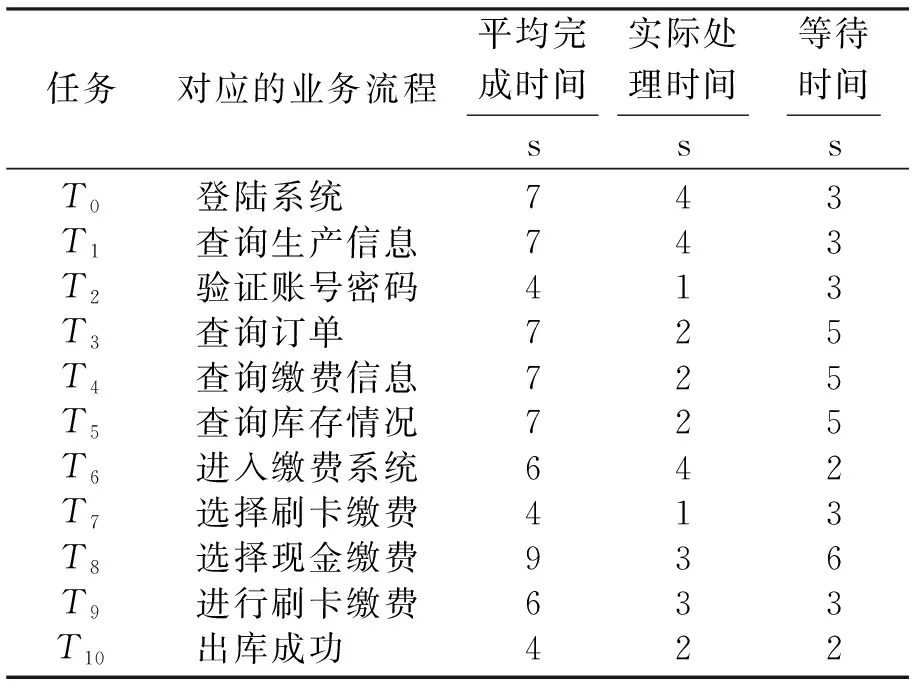
表3 业务流程主要指标

从图2和表3可以看出,当前系统的Petri网结构运行时间较长,内部处理机制效率低,因此在P-不变量的时间分析基础上,运用工作流的并行优化算法对先前模型进行系统优化,优化后的Petri网模型如图3所示.

对优化后的零件出库系统Petri网模型再次进行P-不变量分析,对应业务的处理时间如表4所示.

表4 优化后的业务流程主要指标

图3优化后零件出库系统Petri网模型

Fig.3 Petri net model of outbound system after optimized

综合改善前后的业务流程主要指标如表5所示.

由表5可以看出,业务流程的平均完成时间、实际处理时间与等待时间都相对降低,平均完成时间最多减少了57.1%,因此工作流并行优化算法在提升系统处理速度与减少系统运行时间上具有有效性,且该方法可行.

表5 优化前后业务流程主要指标对比表

5 结 语

本文基于Petri网给出了零件出库系统的工作流模型,根据关联矩阵求解和P-不变量的时间分析,发现当前系统运行方式的处理时间较长,效率低.因此,通过运用P-不变量算法和基于Petri网的工作流并行优化算法重新划分了工作流的结构模型,从而优化零件出库系统的运行时间,提高了系统的工作效率,改善了系统内部处理机制.