基坑开挖对邻近高铁路基变形影响的预测方法研究
2019-02-22方浩
方 浩
(中铁第四勘察设计院集团有限公司,武汉 430063)
随着高速铁路的快速发展与城市地下空间的开发利用程度、规模的迅速扩大,邻近高铁的城市地下空间开发(如基坑开挖)对高铁运营安全的影响,日趋成为一个具有挑战性的关键性技术难题[1-3]。高铁运行时速快,轨道平顺性要求高,对路基变形控制要求极为严格[4]。在邻近高铁路基的范围内开挖基坑,势必引起基坑周边土体变形,进而导致高铁路基变形超过技术要求,会对高铁运营造成重大安全事故隐患[5-6]。

图1 基坑平面(单位:m)
针对基坑开挖对邻近高铁路基变形影响的问题,马宁[3]和朱一康[7]采用数值分析方法,研究了基坑开挖对高铁路基的影响,但未考虑列车动荷载的作用。罗琨等[8]和李梅芳等[9]分析了在列车动荷载作用下,邻近既有线的基坑开挖过程中路基-基坑体系的动变形响应规律。于廷新[10]和王培鑫等[11]基于现场实测数据,研究了路基的变形规律,并提出了高铁侧支护应按变形控制的建议。方浩等[6]研究了降水方案、坑底加固、围护结构插入比以及基坑距路基坡脚距离4个因素对高铁路基变形的影响。上述学者虽然就基坑开挖对邻近高铁路基变形的影响进行了一定的研究,但目前尚未形成一种预测高铁路基变形的简化分析方法。因此,开展基坑开挖对邻近高铁路基变形影响的预测方法研究,已成为当前急需解决的一个技术难题。
以软土地区某邻近运营高铁路基的基坑工程为背景,结合该工程土体修正摩尔-库伦(MCC)模型参数,建立96个不同工况下的有限元模型。通过对有限元计算结果的分析和拟合,推导了能够综合考虑基坑开挖深度、支撑系统刚度和基坑距路基坡脚距离3个因素的高铁路基最大水平位移和最大沉降的简化计算公式,并提出了受基坑开挖影响的路基水平位移、沉降的预测曲线,同时也给出了相应的预测流程。最后采用提出的预测方法对依托工程进行计算,并与实测结果进行了对比,验证了该方法的合理性。本文研究成果可为今后类似工程的安全评估提供参考,这对确保高铁的安全运营和基坑施工的顺利进行具有重要意义。
1 工程背景及参数验证
1.1 工程概况
软土地区某基坑工程拟建二层地下室,基坑周长408 m,面积约8 650 m2,如图1所示。基坑开挖深度10.35 m,局部电梯井挖深11.75 m。基坑周边环境较复杂,西、南两侧邻路,东侧紧邻南北走向的高铁路基,路基坡脚与围护结构边缘的最近距离仅15 m,对变形控制要求极高。该高铁路基为高填方路基,路基总高度为4.7 m,从上到下依次为基床表层、基床底层和基床以下路堤,厚度分别为0.6 m、1.9 m和2.2 m;路基下地基采用搅拌桩进行加固处理。
工程采用钻孔灌注桩+2道混凝土支撑的支护形式,并在钻孔桩外侧采用三轴水泥搅拌桩作止水帷幕。为了控制围护桩的变形以保护基坑东侧的高铁路基,坑底以下5 m深度范围内的被动区土体采用水泥掺量20%的搅拌桩加固,加固宽度4 m。
为确保高铁安全运营、基坑顺利施工,采用了信息化施工技术对工程进行了全程监测,监测点布置情况如图1所示。其中,CX1~CX15为围护桩(土体)侧移监测点,S1~S35为坑外地表沉降监测点,基坑剖面见图2。

图2 基坑剖面(单位:m)
1.2 三维数值模拟
按照工程实际情况建立三维分析模型,模型尺寸详见图3,在此不再赘述。

图3 三维分析模型(单位:m)
模型的边界条件为:上表面为自由边界,底部为固定约束,四周的节点约束法向的自由度。
根据《高速铁路设计规范》[4],高铁路基表面需要考虑竖向荷载,其中线间回填均布荷载强度q0为10.7 kN/m2,轨道结构自重及列车荷载均布荷载强度之和q1为54.1 kN/m2,具体分布情况见图4。基坑四周考虑了20 kN/m2的地面超载[12]。
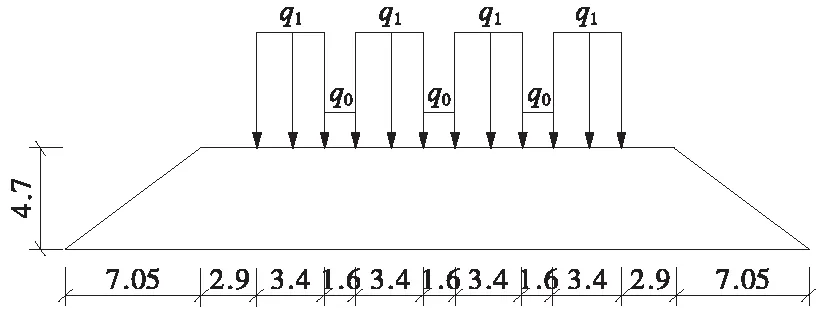
图4 路基面荷载分布(单位:m)
土体采用MIDAS/GTS模型库中所提供的修正摩尔-库伦(MCC)模型[13],该模型是对摩尔-库伦(MC)模型的改进,由非线性弹性模型和弹塑性模型组合,按照加载或卸载的情况输入不同的弹模值,考虑了土体的刚度与应力状态的相关性,可以模拟不受剪切破坏或压缩屈服影响的双硬化行为。因而,MCC模型可以同时获得合理的围护结构变形及其后土体的变形,较适用于基坑工程数值分析[14]。

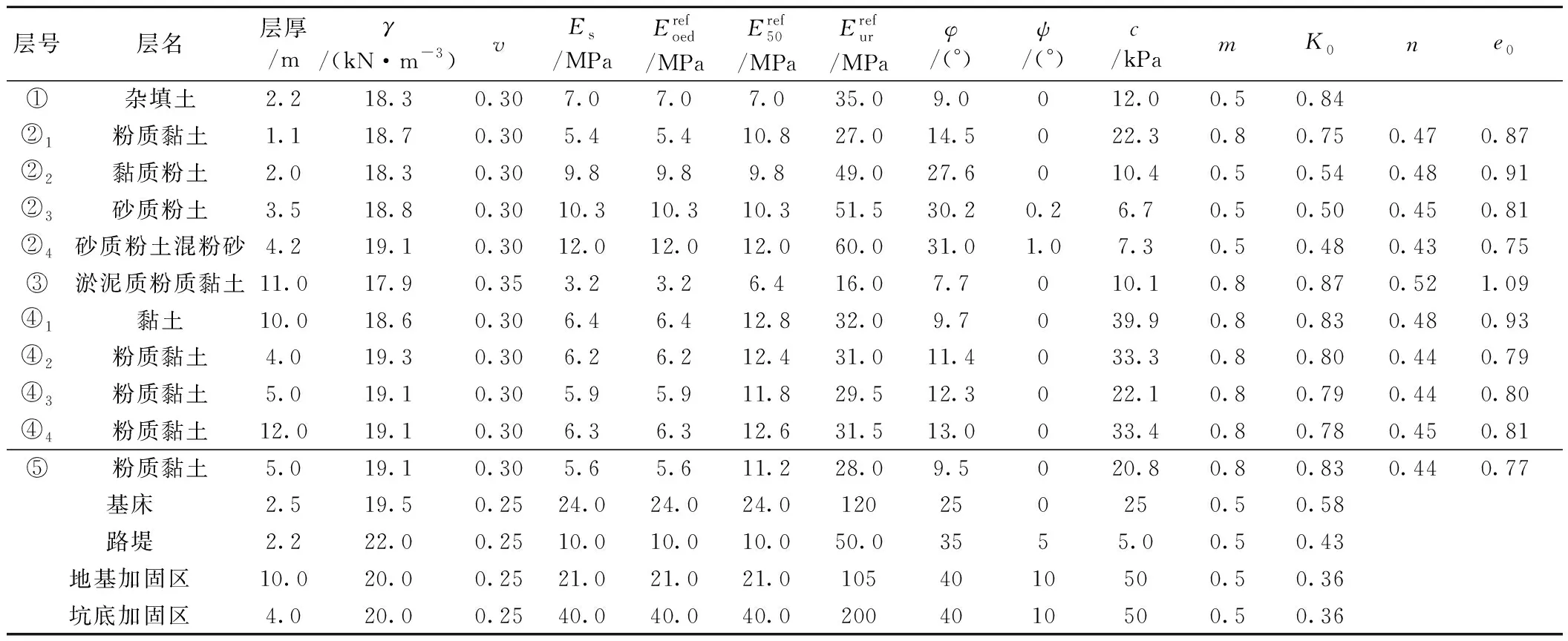
表1 土体MCC模型计算参数
支护结构中钻孔灌注桩、压顶梁、围檩、混凝土支撑以及立柱均采用线弹性模型模拟,混凝土强度等级均为C30,容重γ取25 kN/m3,泊松比ν取0.2,弹性模量E取3×104MPa。钻孔桩采用板单元模拟,其板厚按照抗弯刚度等效的原则确定。其他支护结构均采用梁单元进行模拟。钻孔桩与土体之间的相互作用采用Goodman接触面单元进行模拟,其参数根据刚度折减系数Rinter按相邻单元属性计算而得。
在分析时,通过网格单元的生死来模拟土体开挖以及支护结构施工,通过设置和调整水位线来模拟基坑降水过程,通过替换土体参数来模拟施工过程中对土体的加固。根据实际施工过程,在计算时设置了6个分析步。
1.3 分析模型参数验证

图5 围护结构侧移实测值与计算值的对比
图5为CX4和CX5测点处的围护结构侧移实测值与计算值的对比。图6为地表沉降实测值与计算值的对比,其中图6(a)为靠近高铁侧以S29为基准沿北-南方向所做剖面得到的沉降曲线,图6(b)为靠近高铁侧以S30(见图1)为基准沿北-南方向所做剖面得到的沉降曲线。通过比较可以发现,对于围护结构侧移,侧移最大实测值均位于开挖面以下,计算结果很好地反映了这一现象;深度小于-15 m时,计算曲线与实测曲线吻合较好,深度大于-15 m时,计算得到的连续墙侧移要比实测结果略大;对于地表沉降,计算曲线与实测曲线吻合较好,沉降规律基本一致。总体而言,围护结构侧移与地表沉降的计算曲线与实测曲线的变化趋势基本相似。这表明,本文计算模型及所采用的参数合理可靠,能够较好地反映基坑变形特征及开挖对周边环境的影响,可以在此基础上进一步开展基坑开挖对运营高铁路基变形影响研究,进而提出相应的预测方法。

图6 地表沉降实测值与计算值的对比
2 有限元分析模型介绍
2.1 基本分析模型及参数介绍
为方便后文进行变参数分析,以上述工程实例为基础,重新建立基本分析模型,见图7。
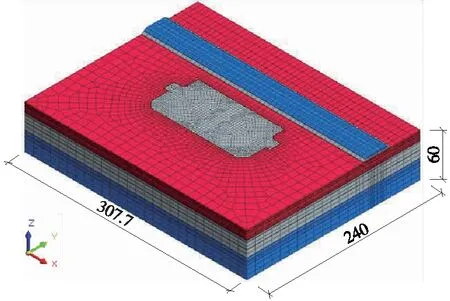
图7 基本分析模型网格划分(单位:m)
基本分析模型中基坑采用地连墙加水平支撑的支护形式。基坑深度取20 m,地连墙深度取40 m。水平支撑竖向间距均为4.5 m,且首道支撑位于地表以下1.7 m处。
为尽量避免模型尺寸效应的影响,基本分析模型的平面尺寸取307.7 m×240 m,其中靠近路基侧基坑边缘到模型边界的距离取93.2 m(4.7H,H为开挖深度),而其余侧基坑边缘到模型边界的距离取80 m(4H);模型的深度方向取60 m。
模型中土体仍采用MCC模型,土体物理力学参数按表1进行取值,土层分布情况见图2。模型中地连墙、围檩、水平支撑等支护结构仍采用线弹性模型模拟,计算参数参照1.2节。
2.2 分析步骤
基本分析模型共设置了8个分析步,具体的分析步骤如表2所示。

表2 分析步骤
2.3 计算工况
根据文献[15-16],场地的土层条件、支撑系统刚度ρ和开挖深度H等是影响基坑变形的重要因素。本文在有限元分析中主要选择支撑系统刚度ρ、开挖深度H和基坑距路基坡脚距离d三个因素展开研究。其中,支撑系统刚度由Clough和O’Rourke[17]提出,其与围护墙体的抗弯刚度及水平支撑的支护情况密切相关,可表达为
(1)
式中,EI为围护墙体的抗弯刚度;γw为水的重度;hs为水平支撑竖向平均间距。
表3为各影响因素取值统计,其中H包含4个变量,d包含4个变量,ρ包含6个变量,共计构成96个计算工况。

表3 影响因素取值统计
3 路基最大水平位移计算结果分析
3.1 路基最大水平位移计算公式
图8为不同基坑距路基坡脚距离下,路基最大水平位移与开挖深度的比值(δhmax/H)与支撑系统刚度ρ的关系曲线。由图8可见,在同一基坑距路基坡脚距离和开挖深度下,路基最大水平位移与开挖深度的比值随支撑系统刚度的增大而减小。其中,当d=20 m、H=20 m时,若ρ从1 670增大到4 750,δhmax/H从0.12减小到0.11,仅仅减小了8%。这表明支撑系统刚度足够大后,通过继续增大支撑系统刚度来控制路基最大水平位移的效果不再明显,且不合理。在d和H不变的情况下均可得到相同结论。

图8 δhmax/H与ρ的关系
由图8可见,在双对数坐标中(δhmax/H)与ρ基本呈线性关系,可用式(2)对两者关系进行拟合。
(2)
式中,a、b为待定系数,具体数值见表4。
由表4可见,每一d值下,a随着H的增大而增大,b随着H的增大而减小。图9(a)给出了a与d/H的关系,并用式(3)进行拟合。图9(b)给出了b与d/H的关系,并用式(4)进行拟合。从中可见,式(3)和式(4)都有很高的拟合精度。
(3)
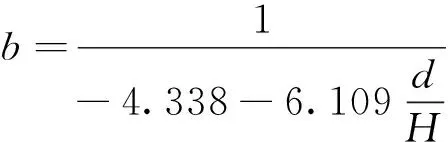
(4)

表4 (δhmax/H)与ρ的关系曲线拟合结果
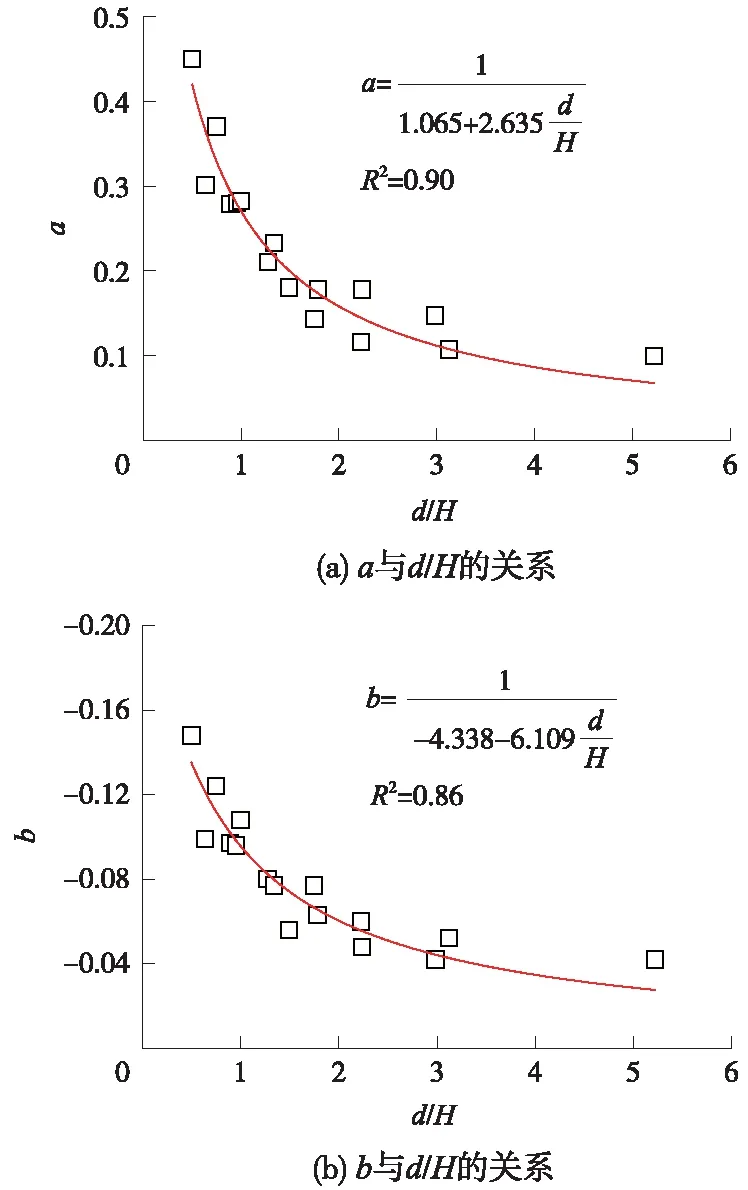
图9 待定系数a、b与d/H的关系
将式(3)和式(4)代入式(2)中,则路基最大水平位移δhmax可表达为
(5)
3.2 路基水平位移预测曲线
图10是不同基坑距路基坡脚距离下的路基水平位移计算结果无量纲化后绘制成的路基水平位移预测曲线。图10中,横坐标为路基水平位移任意点距靠近基坑侧路肩的距离与开挖深度的比值(ds/H),纵坐标为路基水平位移与路基最大水平位移的比值(δh/δhmax)。从图中可以看出,可用折线ABC预测路基任意点的水平位移。其中,点A即靠近基坑侧路肩处,δh/δhmax=0.9;点B即0.5倍的基坑开挖深度处,路基水平位移达到最大;点C即1.2倍的基坑开挖深度处,δh/δhmax=0.95。

图10 路基水平位移预测曲线
4 路基最大沉降计算结果分析
4.1 路基最大沉降计算公式
图11为不同基坑距路基坡脚距离下路基最大沉降与开挖深度的比值(δvmax/H)与支撑系统刚度ρ的关系曲线。由图11可见,在同一基坑距路基坡脚距离和开挖深度下,路基最大沉降与开挖深度的比值随支撑系统刚度的增大而减小。其中,当d=20 m、H=20 m时,若ρ从1 670增大到4 750,δvmax/H从0.20减小到0.18,仅仅减小了10%。这表明支撑系统刚度足够大后,通过继续增大支撑系统刚度来控制路基最大沉降的效果不再明显,且不合理。在d和H不变的情况下均可得到相同结论。

图11 δvmax/H与ρ的关系
由图11可见,在双对数坐标中(δvmax/H)与ρ基本呈线性关系,可用式(6)对两者关系进行拟合。
(6)
式中,m、n为待定系数,具体数值见表5。
由表5可见,每一d值下,m随着H的增大而增大,n随着H的增大而减小。图12(a)给出了m与d/H的关系,并用式(7)进行拟合。图12(b)给出了n与d/H的关系,并用式(8)进行拟合。从中可见,式(7)和式(8)都有很高的拟合精度。

表5 (δvmax/H)与ρ的关系曲线拟合结果
(7)

(8)

图12 待定系数m、n与d/H的关系
把式(7)和式(8)代入式(6)中,则路基最大沉降δvmax可表达为
(9)
4.2 路基沉降预测曲线
图13是不同基坑距路基坡脚距离下的路基沉降计算结果无量纲化后绘制成的路基沉降预测曲线。图13中,横坐标为路基沉降点距靠近基坑侧路肩的距离与开挖深度的比值(ds/H),纵坐标为路基沉降与路基最大沉降的比值(δv/δvmax)。从图中可以看出,可用折线DEFG预测路基沉降。其中,D点即靠近基坑侧路肩处,δv/δvmax=0.95;E点即0.2倍的基坑开挖深度处,路基沉降达到最大;F点即0.6倍的基坑开挖深度处,δv/δvmax=0.85;G点即1.2倍的基坑开挖深度处,δv/δvmax=0.45。

图13 路基沉降预测曲线试验
5 路基变形预测流程及验证
5.1 受基坑开挖影响的高铁路基变形预测流程
前面推导了路基最大水平位移、最大沉降的简化计算公式,并提出了路基水平位移、沉降预测曲线,因此可根据上述公式和曲线预测受基坑开挖影响的高铁路基变形,其预测步骤如图14所示。
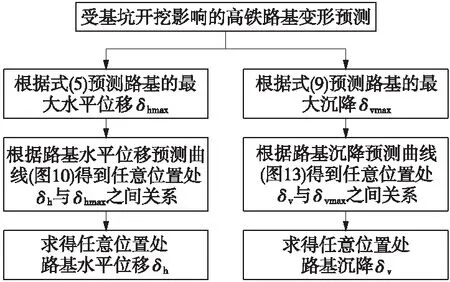
图14 受基坑开挖影响的高铁路基变形预测流程
5.2 受基坑开挖影响的高铁路基变形预测方法验证
按照图14所示的预测受基坑开挖影响的高铁路基变形步骤预测本文依托工程的路基水平位移曲线和路基沉降曲线,并与实测结果对比,见图15。通过比较可以发现,本文方法预测的路基水平位移曲线和路基沉降曲线基本上能与实测结果相吻合。因此,采用本文的方法来预测受基坑开挖影响的高铁路基变形是合理的。

图15 预测的高铁路基变形与实测变形的对比
6 结论
(1)在双对数坐标中,当基坑距路基坡脚距离相同时,路基最大水平位移与开挖深度的比值(δhmax/H)、路基最大沉降与开挖深度的比值(δvmax/H)均与支撑系统刚度ρ基本呈线性关系。
(2)路基最大水平位移δhmax、路基最大沉降δvmax可分别表达为
(3)路基水平位移曲线和路基沉降曲线可分别用图10中的折线ABC、图13中的折线DEFG进行预测。
(4)根据本文提出的预测方法,能较好地预测软土地区类似依托工程土层条件下受基坑开挖影响的高铁路基变形。
