基于数值模型应力提取的并线高铁沉降计算

宋绪国,郭帅杰,陈洪运

(1.中国铁路设计集团有限公司,天津 300251； 2.城市轨道交通数字化建设与测评技术国家工程实验室,天津 300251)

1 研究背景

随着我国高速铁路建设规模的扩大，高铁路网不断加密，工程建设中出现了越来越多的新建铁路与既有高铁交叉、并行与接入工况[1]，如石济客专并行京沪高铁[2]、京唐城际接入津秦客专、商合杭客专并行郑徐客专等。既有运营高铁对轨道平顺性的要求非常严格，新建铁路对临近既有高铁的影响直接关系到其运营的安全性与舒适性[3-4]，工程建设各方均给予了高度关注。现阶段，针对既有高铁附加沉降的控制，主要有轻质土方案[5-6]和应力隔离方案[7-8]，但由于附加沉降理论分析的局限性，当前关于并行高铁的沉降变形评估，主要通过数值仿真方法开展。

值得注意的是，数值仿真模型虽然能够准确模拟复杂荷载和加固地基条件下的沉降变形，但由于仿真模型参数取值范围区间大，部分参数较难获取，导致数值仿真分析结果差别极大[9-10]。此外，数值仿真模型边界条件、地下水、地基土层分层等因素对分析结果也将产生影响[11-14]。因此，有必要针对数值仿真分析方法进行优化，通过数值模型提取地基附加应力，由铁路设计规范推荐的分层总和法完成并行高铁附加沉降评估。

研究过程中，首先，针对数值仿真模型建模参数的取值方法开展研究，依次确定土体模量、土体泊松比、地基分层、地下水位以及模型尺寸对地基附加应力分布的影响规律。之后，以京沪高铁某高铁站为评估对象，研究并行高铁对既有高铁附加沉降的影响规律，验证基于数值模型附加应力提取的并行高铁沉降评估方法的可行性。

2 并线高铁沉降评估方法

高速铁路建设中，为严格控制高速铁路运行期间的工后沉降，地基处理中普遍采用预应力管桩、CFG桩等进行地基加固处理。高铁并线条件下，新建线路荷载将引起既有高铁的附加沉降，对于新旧线路均采用刚性桩复合地基基础和布置应力隔离桩情形[15-16]，应用Boussinesq理论和Mindlin方法对既有高铁附加沉降评估就变得十分困难[17-18]。此种情况下，针对既有高铁的附加沉降评估方法必须从理论上和实践思路方面进行创新。

工程实践中，针对复杂工况的既有高铁附加沉降分析一般采用数值仿真方法，但由于数值模型参数取值的困难性、边界条件的复杂性、荷载条件的多样性，不同人员、不同软件、不同分析方法得到相同计算工况的分析结果完全不同[19-20]。对于同一工况数值模型关于附加沉降的分析结果表现出较大随机性，难以满足并线高铁附加沉降评估要求。

值得注意的是，数值仿真分析模型虽然关于沉降变形分析结果出入很大，但当荷载条件和边界条件相当时，地层附加应力分布趋于一致，并同规范推荐的Boussinesq解答存在相似。基于此，本文提出了一种基于数值仿真模型附加应力提取的并线高铁沉降计算方法。其核心理念为：应用数值仿真分析模型进行复杂工况并线高铁数值建模，依次提取既有高铁线待评估区域深度方向上加载前后的竖向应力，获取对应的附加应力分布，依据铁路路基设计规范中推荐的沉降计算方法，进行既有并线高铁的附加沉降评估。

3 模型参数影响规律及建模方法研究

3.1 数值仿真模型分析中存在的问题

高铁路基沉降分析商业性软件较多，主要分为以Abaqus为代表的有限元软件和以FLAC3D为代表的数值差分软件。数值仿真分析模型建立过程中，主要存在以下几项问题：一是地基模量和泊松比的取值问题，地质勘查报告主要提交土体压缩模量Es0.1-0.2，数值模型主要采用弹性模量，取3～5倍压缩模量，模量参数取值差异，直接导致沉降变形分析结果不同；二是模型尺寸边界的确定问题，模型尺寸边界相对大小将通过边界约束影响模型分析结果，边界过大或过小均会影响分析结果；三是地下水、土体本构以及加载条件等因素综合影响问题。

针对数值仿真模型建模过程中存在的问题，应用Boussinesq理论关于附加应力分析结果，验证数值模型参数对附加应力分布的影响规律，提出高速铁路数值仿真模型建模准则。数值仿真分析软件采用FLAC3D有限差分软件。数值模型建模分析中，路基填高4.5 m，顶部满布10 kPa活荷载，路基顶宽14 m，底宽28 m，典型计算工况(图1)的地基模型横向尺寸L=60 m，地基深度z=40 m。

图1 典型工况数值模型

3.2 地基模量和泊松比影响规律

(1)地基模量影响

地基模量影响分析中，重点分析地基模量差异对地基中心点及填土外区域附加应力分布的影响，通过同Boussinesq理论结果对比，得出地基模量同地层附加应力分布的相关关系。不同模量下，数值模型得到的附加应力分布结果如图2所示。

图2中，不同地基模量下的附加应力分布趋同，模量越大，地基附加应力数值相对也越大，但其引起的附加应力差异一般不大于10%，同Boussinesq理论解的规律趋于一致，相较于Boussinesq理论解的平均偏差最大不超过20%。因此，应用数值仿真模型提取地基土层附加应力中，地基土层模量对附加应力分布的影响基本可以忽略，可不考虑地基模量差异，按照地层实际模量确定模型参数。

(2)泊松比影响

土体泊松比同竖向水平向变形协调关系相关，同类土体的泊松比数值取值较为固定。为验证泊松比大小对地基附加应力分布的敏感性，采用相同方法进行建模分析，不同地基土层泊松比条件下，数值模型关于附加应力分布结果如图3所示。

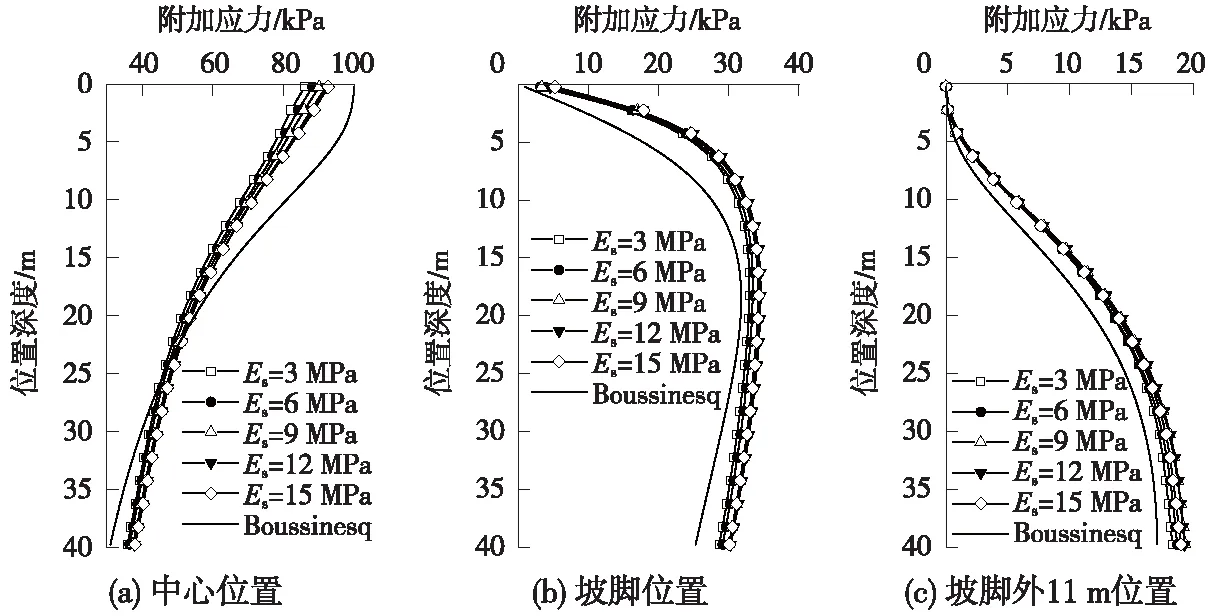
图2 不同地基模量下的附加应力分布

图3 不同泊松比下的附加应力分布

图3中，泊松比对路基中心位置处的附加应力分布影响较为明显，泊松比越大，相应的附加应力也较大，坡脚及坡脚以外区域的附加应力分布差异较小。泊松比引起的附加应力平均差异一般不超过13%，同Boussinesq理论解的平均差异最大不超过20%，当泊松比取值在0.2～0.4时，附加应力分布基本趋于一致。因此，地基土体泊松比对附加应力分布的影响也基本可以忽略。

3.3 模型尺寸的影响规律

数值仿真模型求解中，需要限制模型边界条件，为减少模型边界对仿真分析结果的影响，数值模型的竖向及水平向尺寸必须满足一定范围，模型尺寸过大或过小均会引起数值仿真分析结果的差异。模型尺寸对地基附加应力分布的研究中，具体研究数值模型横向和竖向尺寸对附加应力分布的影响，对应结果分别如图4和图5所示。其中，横向尺寸为单方向尺寸，取模型横向总尺寸的一半。

图4中，填土路堤底半宽为14 m，横向尺寸为20 m时，对地基附加应力分布出现明显偏离。主要由于横向边界条件地基变形的约束导致地基附加应力分布出现偏离，横向尺寸达到40 m时，地基附加应力同Boussinesq理论解较为接近。但是，当横向尺寸过大，地基附加应力分布也将出现偏差，较理论解更为偏小。因此，数值模型建立过程中，单方向横向尺寸建议选取1.5～2.0倍的路基底宽。

图5中，数值模型竖向尺寸差异对地基土附加应力分布的影响更为明显，竖向边界过大或过小均为引起地基附加应力分布的较大差异。竖向尺寸20 m时，附加应力分布结果明显偏离理论解，而当竖向尺寸为60 m左右时，不同位置处的地基附加应力同Boussinesq理论解符合更好。因此，数值模型的竖向尺寸应取路堤填土底宽的2.0倍左右。

图4 横向尺寸对附加应力分布的影响

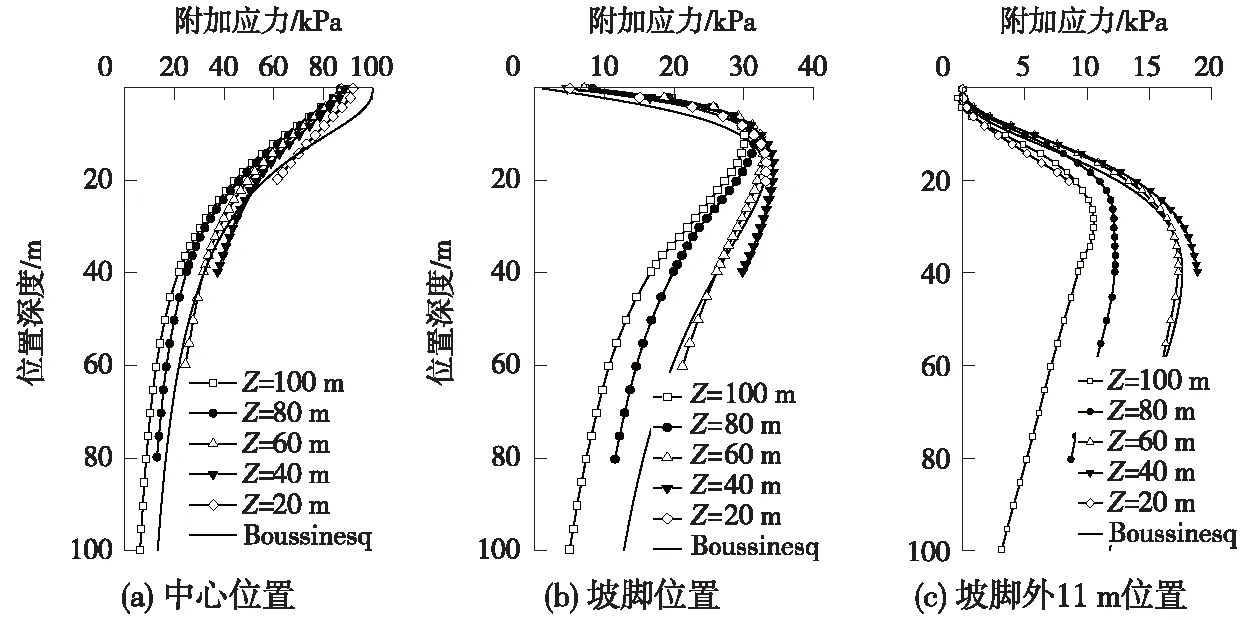
图5 竖向尺寸对附加应力分布的影响

综合图4和图5中模型尺寸关于附加应力分布的影响，数值模型计算中，主要通过边界约束和不平衡力的迭代消除实现平衡状态的解答，模型尺寸过小，边界约束条件将直接影响附加应力分布，进而导致仿真模型结果出现偏差；而模型尺寸过大，必然引起仿真模型单元数量的增加，导致数值模型的最大不平衡力比值减小，数值仿真模型以不平衡力临界比值为结束计算的临界条件时，模型单元数量和最大应力的增加，必然导致最大不平衡力比值的减小，分析结果并未达到最终的稳定状态。因此，数值仿真模型建立中，模型尺寸必须同荷载条件匹配，并非模型尺寸越大，边界影响越小、计算结果越精确的规律。

3.4 土体本构模型、荷载条件及地下水影响规律

(1)土体本构模型和荷载条件

Boussinesq理论本质上是一种弹性解，将荷载简化为矩形、条形分布荷载，但数值仿真分析中提供了丰富的非线性弹塑性本构模型，能够模拟岩土体复杂的应力应变特征，填土荷载往往以实体模型施加。因此，有必要研究土体本构模型和荷载条件对地基附加应力分布的影响。其中，数值仿真分析中的弹塑性模型采用Mohr-Columb模型，荷载条件分为模型加载和等效荷载加载两种。根据数值模型分析结果，不同本构模型和荷载条件的地基附加应力分布如图6所示。

图6 本构模型和荷载条件对附加应力分布的影响规律

图6中，在不考虑地下水和相同荷载条件下，弹性和弹塑性本构模型关于附加应力计算结果趋于一致；而采用等效荷载加载方式的浅层地基附加应力分布同Boussinesq理论解更为接近。因此，应用数值仿真模型进行地基附加应力分布的研究中，可不考虑本构模型的差异，路堤填土荷载条件相对简单时，采用等效荷载，较为复杂时，仍采用实体模型加载方式。

(2)地下水位的影响

地下水位对铁路工程填土路基的影响，主要表现为地下水位以下有效应力的变化，当采用弹塑性模型时，部分区域土体将进入屈服状态，发生明显塑性变形。不同地下水位地基附加应力分布结果如图7所示。

图7中，不同地下水位条件下的地基附加应力分布出现明显差异，但仅当地下水位处于10 m以内时，其对附加应力分布的影响才较为明显，地下水位大于10 m时，附加应力分布趋于一致，且同Boussinesq理论解更为接近。由此，地下水位引起的地基土体塑性屈服，主要发生于10 m以内的浅层土体。因此，应用数值模型进行地基应力分析中，可不考虑地下水位的影响。

图7 不同地下水位条件下的地基附加应力分布

3.5 数值仿真模型建模方法

综合上述地基土体模量、泊松比、模型横竖向尺寸、本构模型、荷载条件以及地下水位对地基土体附加应力分布规律影响的分析结果，应用数值模型进行地基土体应力提取，获得新建路基及临近既有铁路线附加应力，并进行并线高铁附加沉降的评估过程中，应采用如下几项数值模型建立原则。

(1)地基土体根据实际地层参数赋值，弹性模量统一取压缩模量的3倍，刚性桩复合地基基础采用实体桩或桩单元。

(2)数值模型单方向横向尺寸取填土路堤底宽的1.5～2.0倍，竖向尺寸取路堤填土底宽的2.0倍。

(3)数值模型土体不考虑本构模型影响，填土荷载可采用等效荷载或实体荷载，不考虑地下水位位置影响。

4 京沪高铁并线附加沉降分析算例

4.1 京沪高铁并线概况

京沪高铁某高铁站进行扩站改造，进站咽喉区出现大范围的高铁线路并线情况，其中，新建车站采用刚性桩复合地基进行加固处理。京沪高铁附加沉降评估中，地勘报告中关于地层模量参数只提供0.1～0.2 MPa的压缩模量推荐值，直接导入数值模型存在多方面的问题，数值仿真模型关于并线京沪高铁的附加沉降评估结果并不可靠。由此，采用基于数值模型应力提取的分层总和法进行并线高铁附加沉降评估，通过规范推荐的修正系数进行评估结果修正。其中，复合地基复合模量采用《建筑地基处理技术规范》中的确定方法，取加固范围内各分层天然地基压缩模量的4.5倍。京沪高铁某车站并线断面如图8所示，地层物理力学参数列于表1。

图8 新建线路并行既有高铁示意

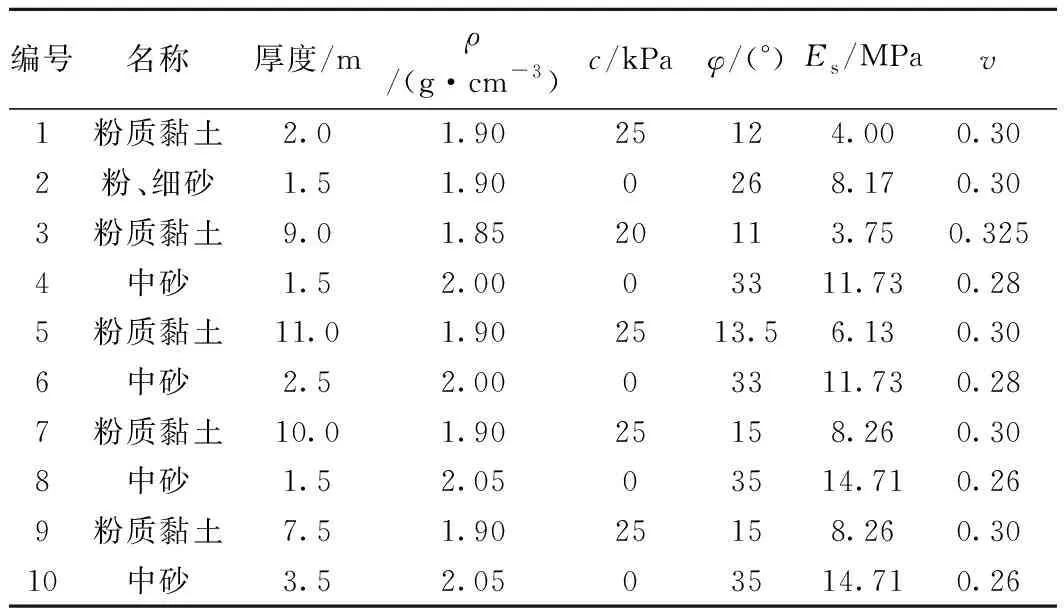
编号名称厚度/mρ/(g·cm-3)c/kPaφ/(°)Es/MPav1粉质黏土2.01.9025124.000.302粉、细砂1.51.900268.170.303粉质黏土9.01.8520113.750.3254中砂1.52.0003311.730.285粉质黏土11.01.902513.56.130.306中砂2.52.0003311.730.287粉质黏土10.01.9025158.260.308中砂1.52.0503514.710.269粉质黏土7.51.9025158.260.3010中砂3.52.0503514.710.26

4.2 数值仿真分析

根据图8中并线京沪高铁的计算断面和表1中的地层数据，采用FLAC3D有限差分软件，建立数值仿真分析模型。地基土采用弹塑性模型，复合地基采用桩单元，不考虑地下水位影响，相应的有限差分数值仿真分析模型及新建线引起的既有高铁附加沉降分析结果分别如图9所示。

图9 数值仿真模型与京沪高铁附加沉降分析结果

4.3 基于数值模型应力提取的沉降评估

图9(b)为数值仿真弹性模量基于6倍土体压缩模量的结果，临近新建线路的京沪高铁坡脚位置沉降最大，远离新建线方向的京沪高铁附加沉降逐渐减小，但由于数值仿真分析模型弹性模量取值的不确定性，数值仿真模型关于京沪高铁附加沉降的分析结果仍表现出较大的不确定性。为克服数值仿真分析结果的上述不确定性，依次提取新建线对既有京沪高铁不同位置处的附加应力，采用《建筑地基处理技术规范》中关于复合地基沉降的相关规定方法，进行既有京沪高铁附加沉降的计算和修正。其中，新建线路引起的京沪既有高铁不同位置处的附加应力竖向分布如图10(a)所示，经等效复合模量修正后的既有京沪高铁不同位置处的附加沉降分布如图10(b)所示，图10(a)中，新建线路引起的京沪高铁不同位置处的附加应力在深度方向上保持递增趋势，但在靠近地表区域出现一定范围的负值分布区。由于地基土不能承受拉应力，且此部分负值附加应力分布区域和数值均较小，运用分层总和法计算既有线路附加沉降时，可忽略此部分负值附加应力的影响。既有京沪高铁复合地基采用复合模量法进行附加沉降评估时，按照承载力提高倍数公式，复合地基的地基复合模量提高为天然地基的4.5倍，对应的地基沉降修正系数为0.2。既有京沪高铁附加沉降经修正后，坡脚位置的最大附加沉降为12 mm，最右侧股道中心沉降4.65 mm，同图9(b)中取6倍土体压缩模量的数值仿真分析结果接近，但验算结果基于规范方法，能够同既有设计经验进行更直观的对比，分析结果更为有效可靠。

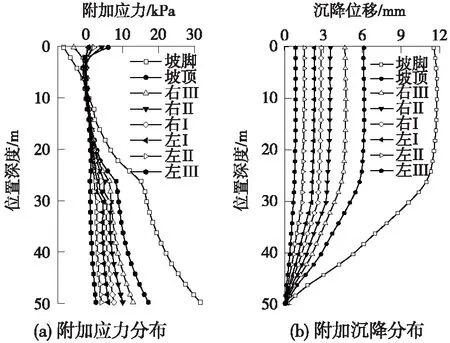
图10 并线京沪高铁附加沉降评估结果

通过本算例关于并线京沪高铁附加沉降的分析结果，研究提出的利用数值仿真分析模型提取复杂工况下既有高铁附加应力进行附加沉降评估的方法，在理论和实践意义上均可行。通过提取附加应力和分层总和法修正方法，严格按照规范，实现了对复杂工况下既有高铁附加沉降的定量评估，在有效避免数值仿真分析模型参数引起分析结果不确定性的同时，也可对照既有规范和设计经验，实现高标准沉降控制条件下既有高铁附加沉降评估。

5 结论

并线高铁附加沉降评估的难点在于现场工况的复杂性和数值仿真模型参数的不确定性，各类因素影响下，导致针对并线高铁附加沉降的定量评估难以开展。经过十多年的发展和经验总结，复合模量法在高速铁路复合地基设计应用中日趋成熟，研究中以刚性桩复合地基复合模量法和分层总和法为基础，确定了影响数值仿真分析结果的各个因素，通过复杂工况下数值仿真模型附加应力的提取，实现了对既有高铁附加沉降的定量评估，并得到以下结论。

(1)数值仿真能满足复杂工况下的并线高铁沉降计算，但受限于模型参数取值的不确定性，并线高铁附加沉降评估不能直接采用数值仿真方法。

(2)基于数值模型应力提取的并线高铁沉降计算方法，能够满足并线高铁的附加沉降评估，并需满足一定的建模准则，数值模型水平与深度边界不应小于1.5倍路基底宽。

(3)数值仿真模型提取地基应力中，不考虑地下水位影响，忽略土体本构模型、土体模量、泊松比、层状地基等因素对地基应力分布的影响。

(4)基于数值模型应力提取的并线高铁沉降评估方法已应用于京沪高铁某高铁站的沉降评估，采用地基土压缩模量和复合地基复合模量，通过规范修正方法，能够满足并线高铁的附加沉降评估要求。