具有精细结构的圆对称爱里光束的传输特性研究

邓攀 刘正楠 耿滔

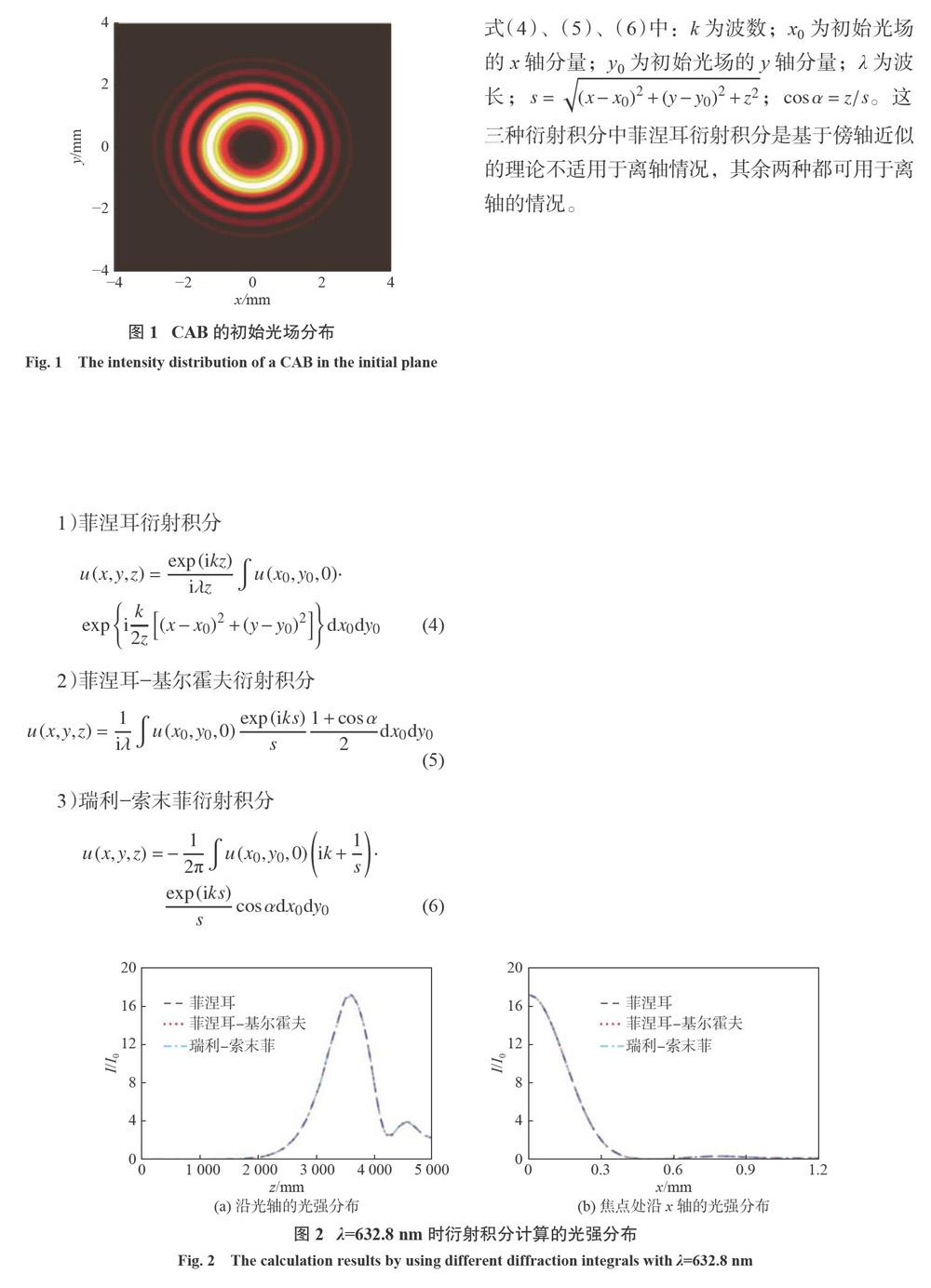
摘要：为了研究具有精细结构的圆对称爱里光束的传输特性，通过减小与光斑宽度相关的参数w，使初始光场具有与波长相近的精细结构。在此特定情况下，用瑞利一索末菲衍射理论对圆对称爱里光束的传输特性进行数值计算。研究结果表明：随着参数w的减小，圆对称爱里光束的精细结构增加，使得代表高频成分的离轴光场影响逐渐增大并参与聚焦行为，焦点光强峰值增大，焦点主光斑的半高全宽减小，突然自聚焦能力得到显著提升;当w减小到某一阈值后，由于持续增加的高频分量进入到倏逝波，焦点光强峰值减小，焦点主光斑的半高全宽增大，突然自聚焦性能下降。

关键词：圆对称爱里光束;精细结构;衍射理论;突然自聚焦

中图分类号：0436.1 文献标志码：A

引言

爱里光束（Airy beam，AB）早在2007年被提出，由于其具有无衍射、自加速、自修复等特性，极大地激发了相关领域科研工作者的研究热情。2010年，基于径向对称性的圆对称爱里光束（circular Airy beam，CAB）被提出，201 1年CAB在實验上得以实。随之进一步提升CAB自聚焦能力的研究成为人们关注的热点。文献【6】将操作波长从可见光移到了太赫兹波段，利用超表面获得了太赫兹波段的CAB，使得光束的自聚焦光斑接近了波长尺寸。这种方法不可避免地使得CAB的初始光场分布具有了与波长尺度相当的精细结构。

在CAB传输特性的理论研究方面，已获得了许多研究成果，但这些研究都默认CAB光场结构是远大于波长的，未考虑精细结构带来的影响。相关资料显示，目前还未有具有精细结构的CAB传输特性的理论研究报道。因此，本文针对这一问题进行了理论研究，以期能更深入地认识CAB的突然自聚焦特性，进一步提升其可应用性。

1CAB传输原理

CAB的初始光场分布表达式为

由于研究者还未能找到满足柱坐标下亥姆赫兹方程或傍轴亥姆赫兹方程的爱里函数解，因此对于CAB的描述还无法给出直角坐标下的解析表达式。目前，对于CAB的传输特性研究，一般采用数值计算衍射积分的方法，所以选取合适的衍射积分方法对于能否得到正确的计算结果至关重要。常用的衍射积分方法有三种，分别是：2讨论分析

图2为使用三种衍射积分得到的光轴上的强度分布，其中λ=632.8nm、Io为入射面初始光强的最大值。从图2（a）中可以看出，三种衍射积分的计算曲线重合，此时自聚焦焦距为fAi=3 579 mm。这一结果与预期符合，因为在可见光波段初始CAB光场的结构远远大于波长，且fAi≥rw，满足傍轴近似的条件，因此这三种衍射积分给出了完全相同的计算结果。由此可见，当初始CAB光场的结构远远大于波长时，三种衍射积分都能给出正确的结果。虽然菲涅耳积分需要附加满足傍轴近似的条件，但当初始CAB光场的结构远远大于波长时，由于其频谱缺乏高频分量，无法获得紧聚焦光束，因此傍轴近似条件自动能得到满足。图2（b）给出了使用三种衍射积分得到的焦点处的光强分布，与图2（a）类似，三种计算曲线同样重合，此时焦点主光斑的半高全宽（the full width at half-maximum，FWHM）约为0.35mm。

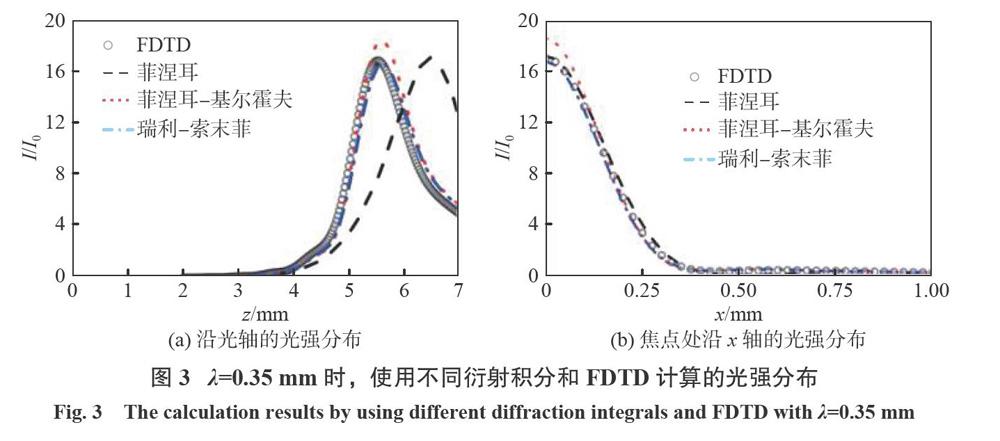
保持其他参数不变，当波长从可见光增长到太赫兹波时，虽然初始CAB光场的分布未发生变化，但波长的增加使得其具有了与波长尺度相当的精细结构。图3给出了2=0.35 mm时，使用三种衍射积分得到的光轴上的强度分布。从图3（a）中可以看到，三种衍射积分的计算结果不再相同，其中使用菲涅耳衍射积分的计算结果与其他两种相比差别较大。为了判断计算结果的准确性，图3（a）同时给出了时域有限差分（finite-difference time-domain，FDTD）的数值仿真结果，通过比较发现其与瑞利一索末菲衍射积分的计算结果基本吻合。此时，使用FDTD、菲涅耳衍射积分、菲涅耳一基尔霍夫衍射积分和瑞利一索末菲衍射积分计算的自聚焦焦距.fAi分别约为5.53 mm、6.45mm、5.59mm和5.62mm。图3（b）给出了三种衍射积分在各自焦点处的光强分布，同时给出了FDTD的仿真结果以便进行比较。从图3（b）可以看出，仍然是瑞利一索末菲衍射积分的结果与FDTD的仿真结果吻合得最好。事实上，对于瑞利一索末菲积分和基尔霍夫理论的优劣之争一直都有争议存在，本文研究的结果是瑞利一索末菲积分的计算结果更加准确。因此在接下来的分析计算中，我们将使用瑞利一索末菲积分。

对于初始CAB光场结构远远大于波长的情况，已有成熟的理论和实验报道，因此本文主要讨论与其不同的、具有精细结构的CAB光场。如前所述，初始CAB的光场分布会随着参数w的变小而变得越来越密，因此可以通过减小w获得光场的精细结构，图4给出了不同w对应的沿x轴的光场分布情况，此时ro=0.2mm，a=0.03。

此外，当λ=10.6um、ro=0.2 mm、a=0.03时，研究CAB焦距.fAi随w变化而改变的情况，w变化范围为0.010 0～0.050 0mm，如图5所示。由图可见：随着w的减小，自聚焦焦距fAi单调递减;当w>0.017 5 mm时，fAi与使用式（2）估算的fest基本吻合;当w≤0.017 5mm时，两者的相对差值急剧增大。由于式（2）是基于傍轴近似得到的，因此可以认为：当w>0.017 5mm时，初始CAB光场缺乏精细结构，其频谱中的高频分量较少，近轴光场占据绝对主导地位，离轴光场的影响可忽略不计;当w≤0.017 5mm后，随着w的减小，初始CAB光场的精细结构逐渐增加，使得高频分量在频谱中的比重增长，导致离轴光场的成分增加，对光束传输特性的影响已不可忽略，此时傍轴近似不再适用。

同时我们也给出了焦点处光强最大值Imax与入射面初始光强最大值Io的比值随w的变化。从图6（a）中可以看到：当w<0.017 5 mm时，焦点光强峰值随着w的增大而急剧增大，在w=0.017 5mm时达到最大值;当0.017 5 mm0.017 5 mm时，FWHM随w的增加而增大。

从上述分析可知：当w>0.030 0mm时，由于初始CAB光场缺乏精细结构，近轴光场占据绝对主导地位，此时焦点光强峰值随着w的减小而缓慢增强;当0.017 5 mm≤w≤0.030 0mm时，随着w的减小，初始CAB光场的精细结构增加，由高频分量产生的离轴光场开始显现作用，光束的自聚集特性得到增强，不仅使得焦点光强的最大值增加，且FWHM随着λ的增长逐渐减小;当w<0.017 5mm以后，随着w的减小，继续增加的高频分量开始进入倏逝波波段，越来越多的光场能量不能传输到远场，使得焦点的能量急速降低，光源使用效率下降，光斑大小也无法进一步减小。

3结论

本文分析比较了三种常用衍射积分的适用性问题，发现瑞利一索末菲衍射积分最适合用来计算具有精细结构的CAB的衍射光场，因此使用瑞利一索末菲衍射积分分析了具有精细结构的CAB的传输特性。研究结果表明：当w逐渐减小时，初始CAB光场开始具有了与波长相当的精细机构，代表高频分量的离轴光场逐渐增加并参与聚焦行为，所以自聚焦能力随着w的减小而增强;但随着w的进一步减小，初始CAB光场的结构开始小于波长，越来越多的高频分量变成了倏逝波，无法传播到远场，使得焦点的能量急速减小，焦点光斑也无法进一步减小，自聚焦能力下降。由于实验条件的局限性，本文未能够通过具体实验来验证数值计算的准确性，还有待进行进一步的研究。