基于无参考图像质量评价的反卷积去模糊算法

王晓红 黄中秋 肖颖 麻祥才 顾思成 赵一铭

摘要：针对数字图像在处理过程中容易产生模糊的现象，提出了基于无参考图像质量评价的自适应反卷积去模糊算法。首先，根据无参考图像质量评价结果与其失真等级的强相关性，通过计算模糊图像的无参考评价参数确定图像的模糊等级，进而根据图像模糊等级与模糊核的对应关系确定反卷积核;其次，提出将失真图像颜色空间转变到YUV，仅对失真图像Y通道进行去模糊处理，保证了彩色图像处理前后颜色的忠实性，并提高算法运算效率;最后，针对图像灰度剧烈变化的邻域出现类吉布斯（Gibbs）振荡分布的现象，提出基于梯度的权重矩阵进行控制。实验结果表明，本文提出的算法在Tid2008图库不仅能够对图像模糊进行快速有效去除，并且恢复图像的纹理细节能够得到有效保留。

关键词：去模糊;反卷积;无参考图像质量评价;YUV颜色空间

中图分类号：TP391.41 文献标志码：A

引言

在信息技术高速发展的当代，图像占人类获取外界信息的70%～80%，图像在生成、传递、压缩、储存和变换等过程中会受到各种因素影响，发生质量退化，从而影响人的视觉效果。在不同失真类型图像的恢复结果中，都不可避免地出现了图像模糊现象，因此本文主要针对模糊图像恢复问题进行研究。

模糊图像恢复算法有很多，从经典的基于最小均方误差的维纳滤波到对模糊模型添加正则化项解决去模糊不适定问题的正则化方法。例如Alanazi等提出基于正则化方法的图像去模糊算法，该方法把待恢复图像看作一个普通的矩阵，没有考虑矩阵元素间的结构连续关系，去模糊后图像难免出现一些视觉上的问题，如振铃问题。Fergus等H提出利用混合高斯模型拟合图像梯度的重尾分布，但该算法会产生严重的振铃效应;Shan等以分段函数拟合图像梯度的重尾分布，并引入局部先验来抑制振铃效应，提高模糊核估计的准确性;Xu等提出利用深度学习进行运动模糊核估计的去模糊算法，虽然对运动模糊失真图像恢复效果有所提高，但去模糊运算时间过长。Xu等提出基于Lo范数的盲去模糊算法，该算法简单可靠，在保证精度的同时显著提升了运算速度，但细节恢复能力不足;Krishnan等提出基于归一化稀疏度量的图像盲去模糊算法，取得了不错的去模糊效果，但其运算复杂度较高，运行速度缓慢;Xu等利用图像先验初始化网络权值，实现了端对端的图像去模糊，但该算法复杂度较高;su等提出基于深度卷积神经网络的视频去模糊方法，但该方法需要学习多帧图像特征，不适用于单幅图像;Wang等提出基于反卷积的分块去模糊算法，虽然使图像处理速度提升，但对于实际模糊核未知的图像处理效果有待提高，因此模糊核的选择对反卷积去模糊算法最为关键。图像模糊的实质就是图像与点扩展函数进行卷积运算的结果，反卷积运算则是一个由模糊图像恢复清晰图像的过程，原理简单，恢复速度快，但反卷积核大小和图像恢复效果直接相关，反卷积核的不合理选择会使得图像出现“弱增强”或者“过增强”。

1算法设计

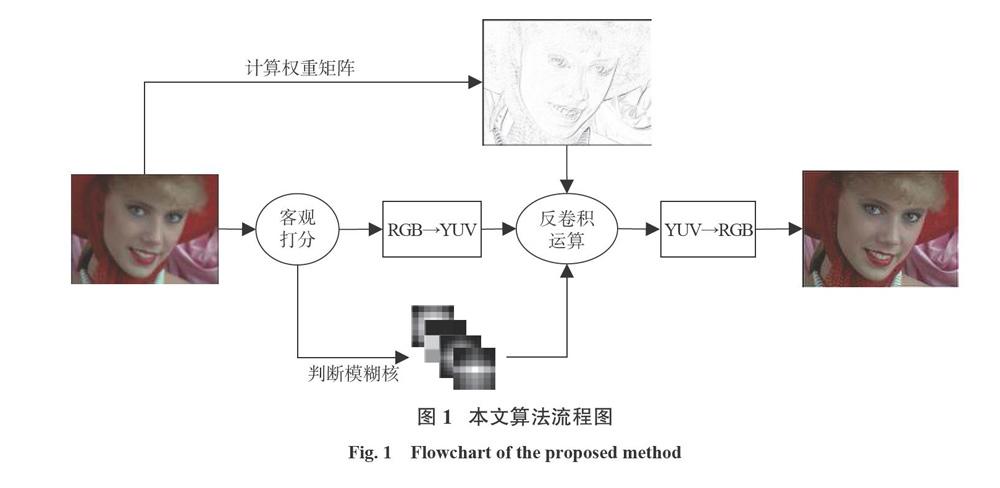
本文选择基于反卷积运算的去模糊算法，对于反卷积核难以确定的问题，提出一种客观方法确定反卷积核，克服根据主观依据对模糊核进行估计的不确定性，算法流程如图1所示。

一幅图像的模糊过程可以描述为

Y=X*K+n（1）式中：y表示模糊图像;x表示清晰图像;*表示卷积运算;K是模糊核，又称点扩展函数（PSF）;n代表图像采集过程中引入的噪声。

从式（1）可以看出，一幅图像的模糊过程可以看作由清晰图像与点扩展函数进行卷积运算并伴随些许噪声。点扩展函数总是一个低通滤波器，即对图像的局部对象进行临近区域像素值平均，使图像失去高频信息而保留低频信息。反卷积是上述算法的逆向运算过程。

1.1反卷积运算

反卷积运算是模糊图像增强中的关键一步，但反卷积核估计是否准确会对图像去模糊结果产生重要影响，如图2（c）所示，反卷积核小于模糊核时图像去模糊效果不明显;当反卷积核大于模糊核时，去模糊后的图像产生严重的振铃效应，降低视觉效果，如图2（d）所示;当反卷积核选择合适时，图像恢复效果较好，如图2（e）所示。

1.2基于无参考图像质量评价的模糊核选择

从图2可以看出，选择不同大小的模糊核对反卷积去模糊运算至关重要。一般而言，图像模糊程度越小，图像质量评价越好;图像失真越严重，图像质量评价越差。据此对模糊失真图像进行失真等级判别，自适应调整反卷积核大小。

图像质量评价方法总体来讲可分为两大类：主观质量评价方法和客观质量评价方法。

1.2.1主观质量评价方法

图像主观质量评价方法被认为是最具代表性的图像质量评价方法，它是通过统计受测者的评价分数均值来判断图像质量的方法，评价尺度见表1。

主观评价结果最接近人的主观视觉感受，结果也最为准确，但主观评价一般需要专业的实验环境以及大量的受测人员，因此成本较高。鉴于实际应用过程，只能采用更加实际和方便的方法，才能获得更好的效果。

1.2.2客观图像质量评价

客观图像质量评价算法简单，计算方便，不需要大量的测试人员及专业的实验环境，因此应用更加广泛。客观图像质量评价方法也可以分为两类，有参考圖像质量评价和无参考图像质量评价。

有参考的图像质量评价方法是通过原图与失真图的相似度得到质量分数的方法。该方法简单易行且种类多。其中最经典的当属峰值信噪比（PSNR）和结构相似度（SSIM），但有参考的图像质量评价方法获取参考图像信息成本较大，因此实用性受到限制。

无参考图像质量评价是没有原始图像信息作为参考的图像质量评估方法。在很多实际应用场合无参考方法更加适用，在本文作为模糊核估计工具更是首当其冲。其中典型算法有盲图像质量指数（BIQI）、盲/无参考图像空域质量评价（BRISQUE）算法和频域空域信息熵评价（SSEQ）算法。

图像是一种视觉产物，图像最终的呈现对象为人眼，因此人眼的视觉打分最能刻画图像质量。本文采用斯皮尔曼等级秩序相关系数（SROCC）、皮尔逊线性相关系数（PLCC）和平方误差（RMSE）对几种图像质量评价算法的客观值与主观值之间的准确性、单调性、一致性和区分率进行评价，结果见表2。

在表2中可以发现SSEQ算法的SROCC和PLCC系数值比其他算法更接近于1，表示SSEQ评价算法和人的主观评价分数更加接近，说明SSEQ算法性能更优;而且SSEQ算法的RMSE值低于其他算法，充分说明SSEQ算法用于模糊图像失真评价的准确性。区分率（D）表示某一等级图片区别于其他等级图片的概率，公式如下：

本算法中D代表某个模糊等级图像能够区别于其他等级图像的概率，是本文选取模糊核的关键。综合比较这四个参数的值，SSEQ算法区分率最高，能够对不同失真等级的图像进行较为理想的区分，又鉴于全参考方法很难获得参考原图，因此选用SSEQ算法进行反卷积模糊核估计。通过SSEQ算法计算具体数值与人眼平均主观得分（MOS）后进行比较，结果见图3。

通过SSEQ算法的评价分数和主观评价分数对比图可以看出，SSEQ计算得出的数值与人眼评价契合度高，能够忠实代表人眼评分，因此作为模糊核选择方法的SSEQ算法能够精确选出模糊核。

1.3优化算法设计

单步的反卷积去模糊处理方法都不能得到理想的恢复效果，存在去模糊处理速度慢、颜色忠实性差和振铃效应等问题，因此需要对本文算法进行进一步优化，以获得性能更佳的去模糊处理算法。

1.3.1保持颜色忠实性的快速运算优化

彩色图像具有多个通道，一般彩色图像处理方式大都是分通道单独处理。不考虑通道间的相互作用，容易使得处理后图像发生颜色失真。本文提出转变图像默认颜色空间RGB到YUV，使图像颜色信息与亮度信息分离，保证颜色信息不改变，分通道提取直方图如图4所示。

图4（a）是高清图的Y通道分量，可以看出像素在各个阶调分布比较均匀，u分量[图4（b）]与v分量[图4（c）]的像素值主要分布在暗调。根据人眼对暗调变化感受不明显、对轻微的亮调变化反应明显的视觉特性，本文提出仅对Y通道进行图像去模糊处理，从而保护颜色忠实性，保证了去模糊质量，且提高了运算效。

1.3.2去除振铃效应优化算法

振铃效应是指在图像灰度剧烈变化的邻域出现类吉布斯分布的振荡，因此找出图像灰度剧烈变化的区域成为去除振铃效应的关键。本文采用梯度作为定义边缘的关键。梯度的本意是表示某一函数在某点处的方向导数沿着该方向取得最大值。因此在图像灰度剧烈变化的地方，梯度值较大;在图像灰度缓慢变化的地方图像梯度较小，因此可用图像的梯度矩阵反映图像边缘变化情况。以7x7大小模糊核对图片进行模糊处理，在图片进行反卷积去模糊的过程中，相邻边缘像素值对中心像素值的贡献不同，即根据基于梯度的权重矩阵对模糊图像对应位置的反卷积进行权重控制，最终减小并去除图像振铃效应。

本文选择模糊图像水平与竖直方向梯度的均值作为权重矩阵，图5为去模糊算法中添加梯度权重矩阵与不添加梯度权重矩阵的效果对比图。

2实验结果

采用图6所示10幅图像作为原图，对原图采用标准差为3，大小分别为5x5、7x7、9x9三个等级尺寸的高斯模糊核进行模糊，生成测试图像。

不同等级模糊图像进行去模糊处理的仿真结果如表3～5所示。

表3～5中“图像1，图像2，……”代表不同的图像，“PSNR-mohutu”代表模糊图的峰值信噪比，“PSNR-huifutu”表示去模糊后图像的峰值信噪比，“SSIM-mohutu”代表模糊图像的结构相似度，“SSIM-huifutu”表示去模糊后图像的结构相似度，“SSEQ yuantu”代表未失真图的SSEQ算法打分，“SSEQ mohutu”表示模糊图的SSEQ算法打分，“SSEQ huifutu”代表去模糊后图像的SSEQ算法打分，“SSEQchazhi”表示去模糊后图像的SSEQ值与原图的差值。从表3～5可以看出，去模糊后图像峰值信噪比与结构相似度提升明显，且SSEQ打分与原图充分接近，根据主观质量评价表可以看出去模糊后图像与未失真图像人眼评分的差值大都在20分之内，充分表明去模糊后图像可以达到“非常好”的恢复效果，满足图像处理要求。选择年龄在21～25岁之间、男女比例1：1的20名视觉正常观察者对去模糊后图像进行主观评价实验，通过比较无失真图像和失真图像评价得分的差异，进一步验证本文去模糊算法的有效性，得出人眼的平均主观得分差（DMOS），结果如表6所示。

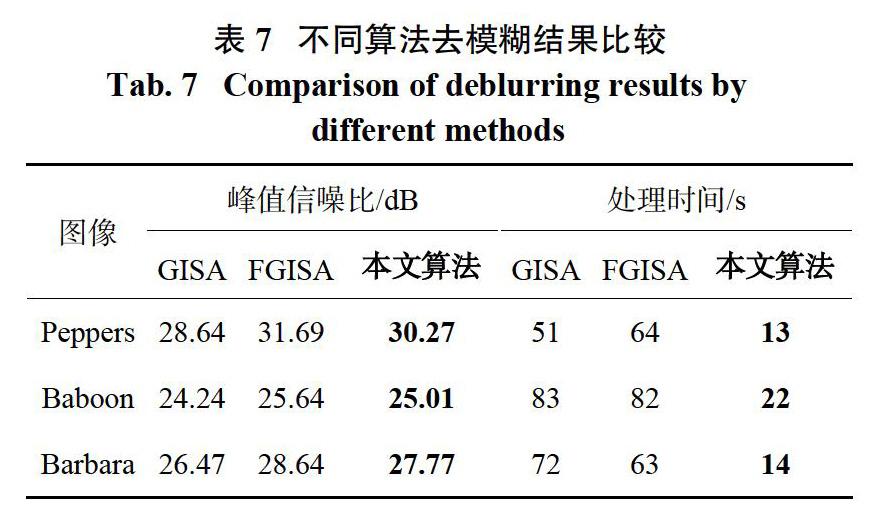
通过实验结果可以看出，基于无参考图像质量评价的自适应反卷积去模糊算法对模糊图像具有较为理想的恢复效果。由于目前大多去模糊处理算法都选用峰值信噪比PSNR作为评价指标，本文分别与GISA算法、FGISA算法进行去模糊性能比较，比较结果见表7。

通過表7对比可知，本文提出的去模糊算法在保证去模糊后图像质量的同时提高了去模糊效率，减少了去模糊恢复时间，能够有效快速地对模糊图像进行去模糊处理。

3结论

本文提出基于反卷积运算的快速去模糊算法，使用客观方法对不同模糊等级的图像进行评价打分，从而自适应选择不同大小模糊核进行去模糊运算。针对去模糊运算中出现的振铃效应，本文提出基于梯度的权重矩阵进行优化，同时对于图像处理前后颜色忠实性差、运算速度慢等问题，本文采用转变颜色空间处理方式予以解决，从而在保证图像去模糊质量的同时，提高去模糊运算效率。