全波形激光测距幅相误差改正方法

刘荣荣 毛庆洲

摘要：针对全波形激光测距中存在的幅相误差问题，提出一种基于神经网络的幅相误差改正方法。利用非合作目标探测信息，通过提取回波波形的形状信息、能量信息、梯度信息、对称性信息及距离信息特征参数，根据皮尔逊相关系数对特征参数进行分级，建立多回波特征信息与幅相误差改正的神经网络模型以校正全波形激光测量中各通道幅相误差的影响。实验使用5%、20%、60%、80%标准反射板及激光采集模块在室内对7种距离进行数据分组采集和处理，并与传统测量方法进行对比。结果表明，该方法可以有效减小全波形激光测量中幅相误差的影响，测量精度提高了51.2%以上。

关键词：全波形激光雷达;幅相误差;神经网络;回波特征提取;信号检测

中图分类号：P207 文献标志码：A

引言

全波形激光测距是一种典型的非合作目标距离测量与反射强度获取方法，在国土测绘、军事侦察及工业测量等领域中发挥着重要的作用，其测量精度及效率在激光测量中广受关注。幅相误差是高精度激光测量中的重要误差来源，主要是由各通道回波幅值不同引发的检测相位变化引起。

针对幅相误差这一问题，Palmese等提出在有源校正前提下的幅相誤差解决方法;Friedlander提出了一种阵列幅相误差迭代算法来避免计算校正源;王鼎等构造二次代价函数，通过反复迭代求解估计幅相误差;郑煜等利用雷达的杂波特性提出一种基于杂波子空间特征的雷达幅相误差自校正方法以解决幅相误差较大的问题，但是算法的适用范围有限;杨璋等针对均匀线阵和圆阵给出了幅相误差自校正方法，但迭代算法计算量较大，计算效率有待提高。本文提出一种基于神经网络的全波形激光测距幅相误差改正方法，通过建立波形特征信息与幅相误差的改正模型准确计算幅相误差的改正量，以降低幅相误差的影响，提高测量精度。

1全波形激光雷达测量原理

1.1测量原理

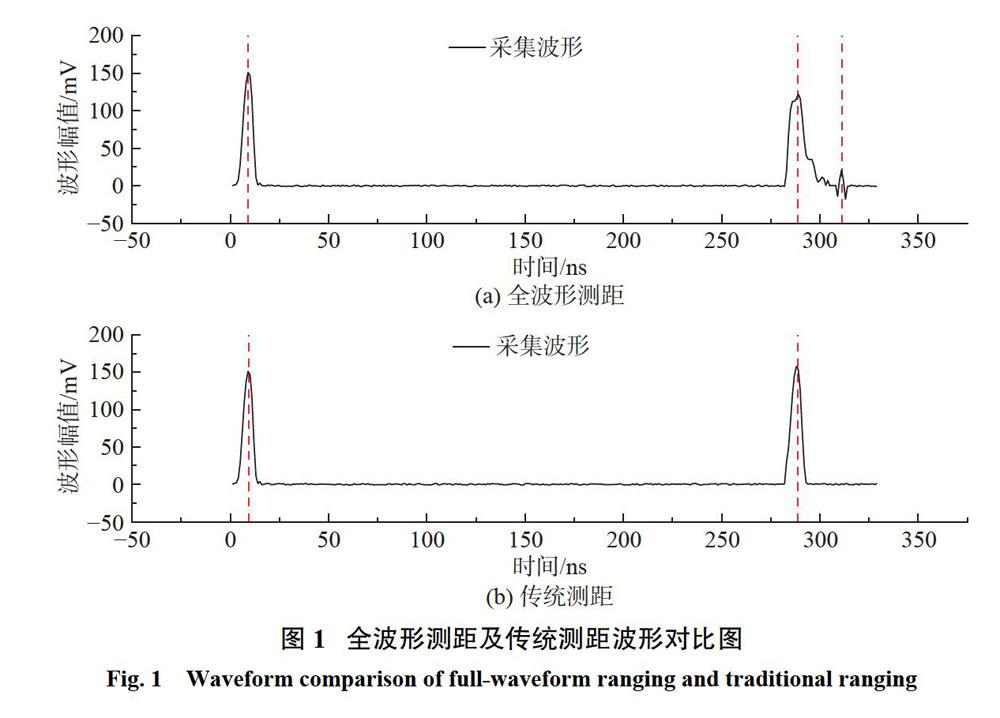
全波形激光雷达发射单次激光脉冲后，对发射脉冲及激光脚点内探测目标的后向散射回波进行全数字化记录和存储，不仅能够实现高精度测距，还能提供丰富的地物垂直结构信息，如图1所示。通过分析其脉冲相位、幅度、脉宽及脉冲个数等全波形回波特征信息，可以挖掘更深层次的地物属性信息。

与传统激光雷达测量相同，激光发射器向探测目标发射激光信号，再由信号接收器接收来自探测目标的后向散射信号，通过记录激光器发射种子光时刻to与回波接收时刻t1，即可计算激光发射位置与探测目标之间的距离D，D的表达式为

为精确计算回波信号至种子光信号的时间差，目前已有的方法包括峰值法、加权法、重心算法及高斯拟合中心法等。由于全波形回波信号并非典型高斯回波，直接使用上述方法计算飞行时间存在偏差，使测量精度降低。本文结合多种波形中心计算方法与波形特征信息，建立神经网络模型以准确计算脉冲飞行时间。

1.2幅相误差

在全波形激光雷达信号处理中，由于激光雷达测量环境及目标的多样性及复杂性，不同地物测得的反射信号具有各自的特殊性，这些回波的波形特征包含了除测量距离外的大量地物属性信息及测量环境信息等。全波形信号经过波形分解、峰值检测等算法可得到收发信号的时刻坐标，初步计算测量距离D。

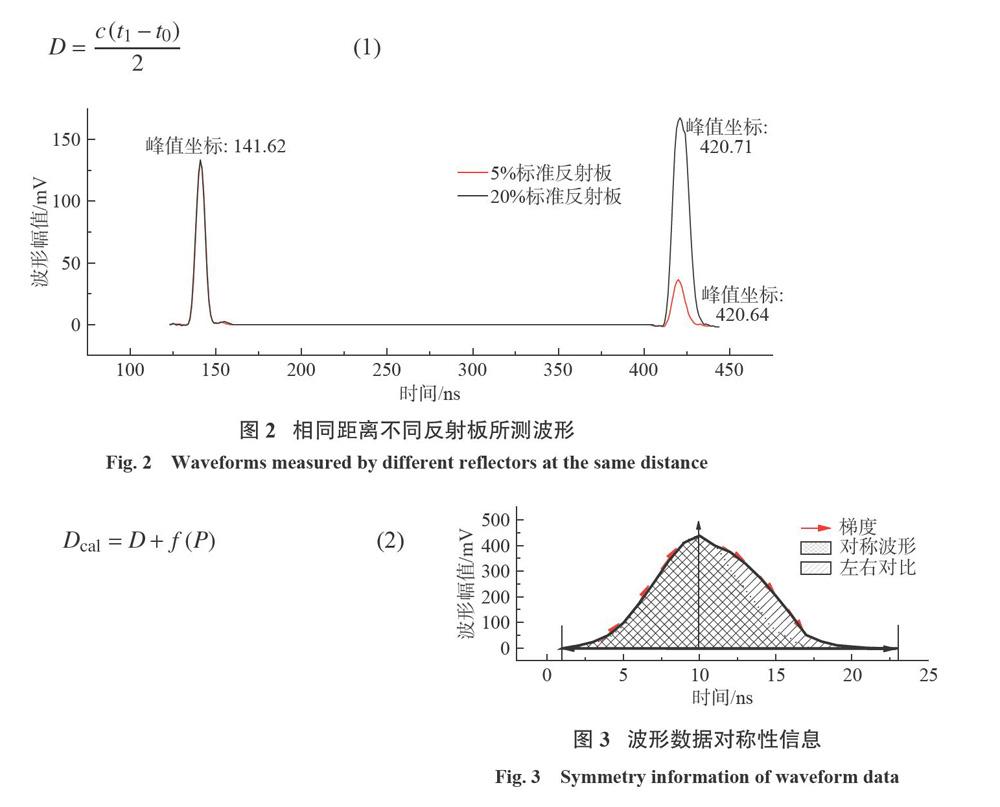
不同通道探测到的回波幅值及相位不同使检测到的回波峰值位置发生变化，极端情况下由幅相误差带来的测量误差可达厘米级以上。在室内相同距离分别使用5%标准反射板、20%标准反射板及激光数据采集模块采集种子光及回波波形数据，5%标准发射板对应波形及20%标准反射板对应波形的种子光对齐后，两组回波幅值及相位均有差异，峰值检测位置发生“前后漂移”，如图2所示。

1.3波形特征

幅相误差使得实测中不同距离回波信号的形态特征发生不同程度的变化，直接由式（1）所得的测距信息D受幅相误差的影响。为消除幅相误差的影响，可根据回波波形的形态特征信息P、测距信息D与幅相误差建立网络模型厂（P），求解幅相误差改正数，以计算改正后的测距值Dcal：

波形信号的特征信息主要包括形状信息、能量信息及对称性信息等。全波形信号并非严格意义上的高斯型波形，其左右往往呈“此缓彼陡”的非对称形态。为表征这种非对称性信息，一是使用上升沿及下降沿的梯度信息，二是使用回波峰值左右半部向量差值表示，如图3所示。

为表征探测波形在不同通道的形态变化，共选取9类波形特征：回波峰值、宽度、能量、平均值、峰值位置、重心位置、上升沿及下降沿梯度信息、回波对称性信息及距离信息。假定波形处理后获取的有效波段为E（e1，e2，…，en），ei为i（i=1，2，...n）时刻采集的波形幅值，则：

1）回波峰值：使用波形幅值最大值及其左右多个波形幅值点，计算加权后回波峰值;

2）回波宽度：根据有效波段检测阈值，计算回波有效范围;

3）回波能量：计算有效波段内波形面积;

4）平均值：计算有效波段内幅值的平均值;

5）峰值位置：计算回波峰值对应的时间坐标;

6）种子光与回波中心距离信息：使用高斯函数拟合种子光波形及回波波形，计算波形中心位置坐标时间差;

7）回波对称性信息：使用三次样条插值使左右半部的回波向量维度相同，通过计算左右向量差值向量的范数来表征对称性信息，符号信息由峰值左右波形面积比值赋予，当左面积与右面积比EI/Er≥1时，符号sig=1，反之sig=1;

8）回波重心位置：单一使用高斯拟合在波形采集点较少时会发生“左右漂移”，因此使用迭代法计算回波波形面积二分之一处的时刻坐标来表征回波重心位置;

9）上升沿及下降沿梯度信息：使用4阶切比雪夫多项式拟合回波曲线，将上升沿（起始点至峰值点）平均分为4个区间，选择中间3个位置计算拟合曲线上的1阶梯度信息，同理可计算得到下降沿梯度信息。

2波形数据处理方法

2.1波形处理

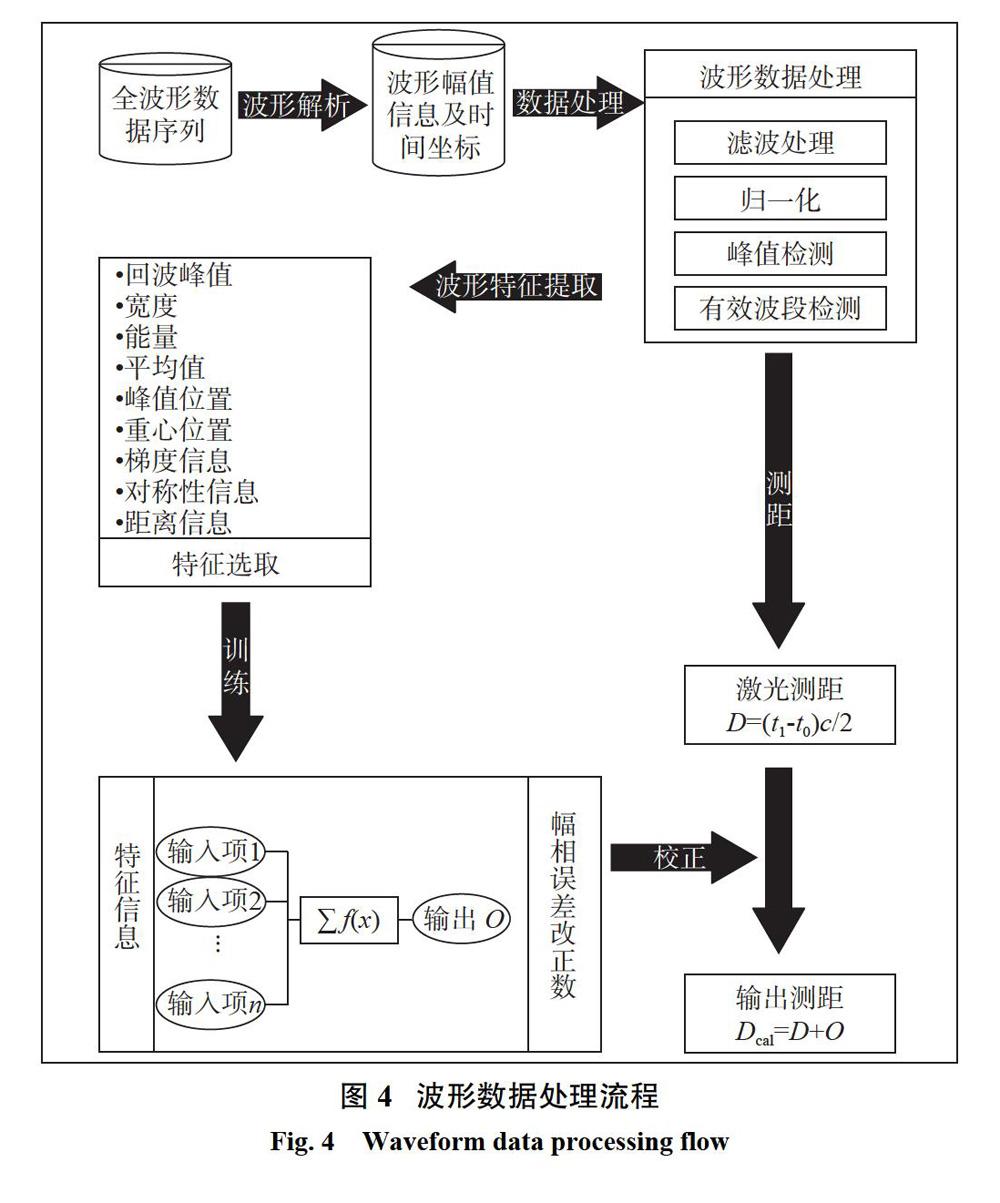
用激光测距仪采集原始波形数据（由十六进制的特定数据结构组成），对这些数据解析后得到波形幅值及时间坐标信息;再对波形信息进行滤波处理以消除噪声，同时采用二阶导数方法检测波形的有效信息段，以及对有效波段进行数据归一化（以便后续结果对比）;最后经提取波形特征及分类后，交由后向传播（BP）神经网络处理并对测距结果进行改正。处理流程如图4所示。

2.2相关性分析

经过波形处理后，从有效波段中提取的波形特征共9类。为减少数据冗余量，提高数据处理效率，需要从9类信息中提取最典型的特征信息。皮尔逊相关系数适用于分布不明、非等间距测度的连续变量情况，其定义为两个变量之间的协方差和标准差的商。假定向量X，y，则其皮尔逊相关系数p计算公式为

实际测量中使用5%、20%、60%、80%标准反射板在不同距离处进行测量，可以看出不同波形特征信息在不同反射率下的变化有所差异。极强相关的波形特征在4种标准反射板下出现较为明显的4层分段现象;中等程度相关的波形特征也会出现不同程度（3层及以下）的分层现象;极弱相关的波形特征在不同反射率下变化很小，基本呈现一条线，如图5所示。因此，在后续进行神经网络训练时，输入项的选择有：1）选择3类极强相关特征;2）选择3类极强相关特征和2类中等强度相关特征;3）选择所有的9类特征。

2.3神经网络

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，其特点就是信号的前向传播与误差的反向处理，根据层输入项计算层输出，再根据计算值与真实值之间的误差调节参数，直至训练误差满足条件。神经元模型可以简化为Oj=f（netj））=f（wj^Tx），其中：W为输入项的权重向量;Xl，X2，X3，…，Xn为神经网络输入项，即各类波形特征信息;D为神经网络输出项，即幅相误差改正数。

根据在不同反射板下各波形特征变化大小，设置3种输入量：1）使用极强相关的3类特征，即总能量、峰值及平均幅值;2）在1）基础上增加中等程度相关特征，即对称性信息以及距离;3）使用全部9类波形特征信息。使用80%的实测数据为训练数据，20%的实测数据为测试数据，检验神经网络模型的可用性及准确度。

3实验与分析

3.1实验数据采集

实验在室内基线场进行，实验场布置如图6所示。使用全波形激光数据采集模块、标准板固定支架及4块标准反射板（5%、20%、60%、80%）采集波形数据，采样频率为1.2 GHz（1 clock=0.8333 ns，为相邻采样点的时间间隔），共4个通道，相邻通道间放大倍数为16倍，由十六进制数据格式存储原始波形，波形解析后可得到波形幅值及时间坐标信息，经过波形处理后参与BP神经网络训练学习。

真实距离数据使用徕卡全站仪TS1115获取，使用支架固定4块反射板，选择7处采集波形数据，共28组数据，每组数据包含1 000对种子光及回波波形数据，共28 000条数据。BP神经网络使用采集数据中的80%作为训练数据，20%作为测试数据。图7所示为相同距离处不同反射板所测得的种子光及回波波形数据，5%及20%标准反射板所测数据由4通道获取，60%及80%标准反射板所测数据由3通道获取。

3.2实验结果

根据2.3节，对9类波形特征重要性大小进行分级，建立波形特征与幅相误差改正的4层BP网络模型;依据3类神经网络输入项分别输入波形特征信息，根据网络输出对测距进行校正，并与传统直接计算激光测距的重心法进行对比，比较处理前后脉冲飞行时间的分布。每组测试数据800条，0～200，201～400，401～600，60 1～800对应的飞行时间分别为使用80%、60%、20%、5%标准反射板所测数据，如图8所示。

3.3结果分析

波形幅相误差改正精度使用两类评价参数：一为改正前后激光飞行时间分布的标准差，二为改正前后使用不同反射板在相同距离处1 000次测量的平均值与真实距离之间的最大误差。表2、3表明使用文中方法减小了测距点分布的离散程度，使用不同反射板测得的最大误差可减少51%以上。使用5类特征参与模型训练即可得到较好的结果，说明使用该方法处理幅相误差是可行的。

4结论

幅相誤差是高精度激光测量中必须考虑的误差来源，为减少幅相误差对激光测量精度的影响，本文提出了一种基于神经网络的幅相误差改正方法。通过提取波形的多项特征信息建立幅相误差改正的神经网络模型;使用皮尔逊相关系数表征各波形特征在不同反射率下的变化大小，将波形特征分成3类分别输入网络模型进行训练;以80%的实测数据输入到BP神经网络进行训练，使用剩余20%实测数据进行测试。实验结果表明，该方法可以有效减小幅相误差的影响，多次重复测量可以减小测量数据的离散程度，提高测量精度。实验存在的问题有：只使用4块标准反射板并在室内进行，缺少对长距离、多反射率情况中幅相误差的分析;缺少对种子光特征的分析，未来可以从深度学习的角度出发，挖掘种子光及回波数据更深层的特征信息以减少幅相误差对测量精度的影响。