坝体加高对粘土心墙坝的影响研究
2019-02-21刘世伟费文平邹海鸥
刘世伟,费文平,邹海鸥
(四川大学水利水电学院,四川 成都 610065)
1 概述
粘土心墙坝作为坝工建设领域中非常常见的坝型之一,具有对地质条件要求低、就地取材、造价低、施工速度快及抗震性能好等许多优点,在当前坝工建设中得到了非常广泛的应用。与此同时,随着建坝的数量日益增多,由此产生的工程问题引起了国内外许多学者的关注并进行了大量研究。刘松涛[1]采用有限元方法分析了三峡茅坪溪防护工程粘土心墙方案的应力应变;姜海波[2]通过室内试验和三轴试验测得坝体材料的物理性质指标和邓肯张E-B 模型参数,采用有限元方法计算并研究分析了竣工期和渗流稳定期高土石坝坝体应力、应变和变形;熊鹏、刘超群等[3]人基于邓肯-张非线性弹性材料模型,对云南省某在建粘土心墙堆石坝逐层填筑施工和正常蓄水+9 度地震作用两种工况情况下的坝体应力和变形进行了有限元数值模拟与分析;沈珠江、王剑平[4]运用5 种不同的土石料应力应变模型进行了数学模拟,论述了几种模型的优缺点及土石坝应力应变分析中存在的问题。由此可见,粘土心墙坝的设计建设中,采用有限元数值模拟方法对坝体在施工和蓄水中的应力-变形进行计算与分析非常必要,已被我国坝工界所认可。本文基于邓肯-张非线性弹性材料模型,运用有限元数值模拟方法对大坝完建工况下的坝体及粘土心墙的应力和变形进行了有限元静力分析,以为该坝体的安全性、稳定性评价提供依据。
2 邓肯-张E-μ 模型及二次开发
基于ANSYS 软件的有限元计算,采用邓肯- 张E-μ 模型,模型中的弹性模量E 的计算如下式:
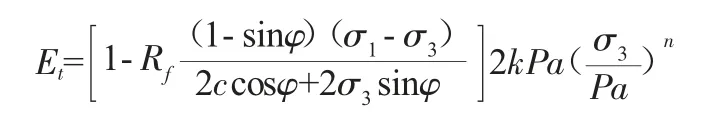
式中:c 为材料凝聚力;φ 为材料内摩角。切线泊松比μt的表达式如下:
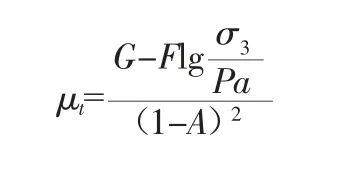
式中:A=D(σ1-σ3)/Et、D、G、F 为材料参数。对于卸载情况,该模型采用回弹模量Eur进行计算。回弹模量表达式为:
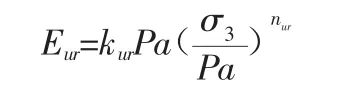
式中:kur为卸载模量基数,nur为卸载模量指数,且一般情况下nur≈n;当σ1-σ3小于历史上的最大值(σ1-σ3)0,且s 小于历史最大值s 时用Eur,否则用Et。
APDL,即ANSYS 参数化设计语言,用其编写邓肯- 张E-μ模型的宏命令,然后赋予材料初始值,反复调用宏命令,反复计算,最终得到合理的弹性模量、泊松比,最后再计算坝体的应力应变。
3 粘土心墙坝三维有限元模型
3.1 工程概况
本文研究的是某水库大坝的加高工程,原大坝为粘土心墙风化料坝,坝顶高程1285.40 m,最大坝高58.4 m。大坝加高选择从下游坝坡加高培厚的方式,加高后新加高坝为粘土斜墙风化料坝,坝顶高程为1293.80 m,最大坝高66.80 m。粘土斜墙底部与原坝体心墙顶接合,斜墙底高程1281.88 m。上游斜墙坝坡1∶2.5,下游坝坡1∶2.25、1∶2.0、1∶2.0。标准剖面图见图1。
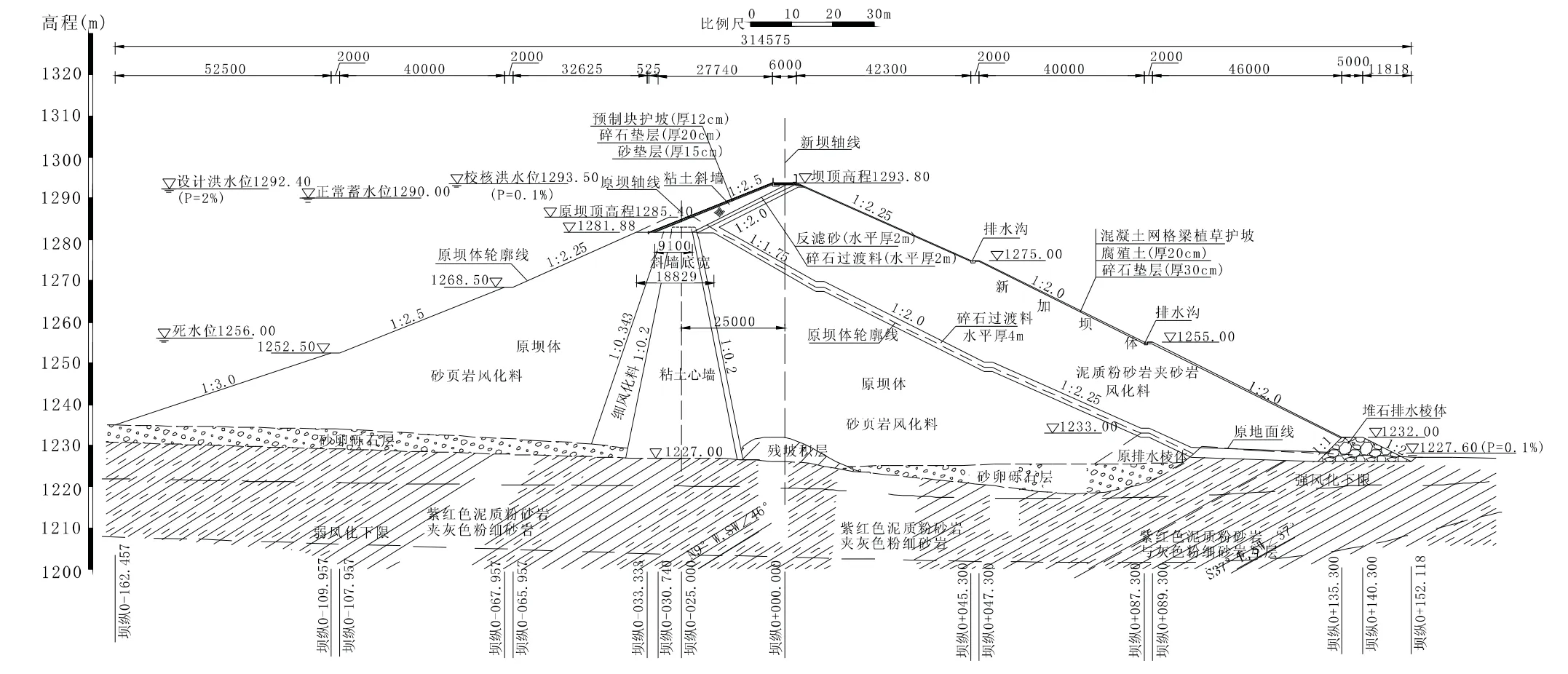
图1 大坝标准横剖面图
3.2 计算参数与荷载
不考虑蓄水及其它外部条件的荷载,只考虑大坝完建期自重荷载的工况。
计算采用的单元为六面体SOLID185 实体单元,在材料参数设置上,针对不同的材料特性,静力计算过程中主要考虑了两种材料本构模型,对基岩采用线弹性模型,对坝体材料采用邓肯- 张非线性模型,材料参数见表1。
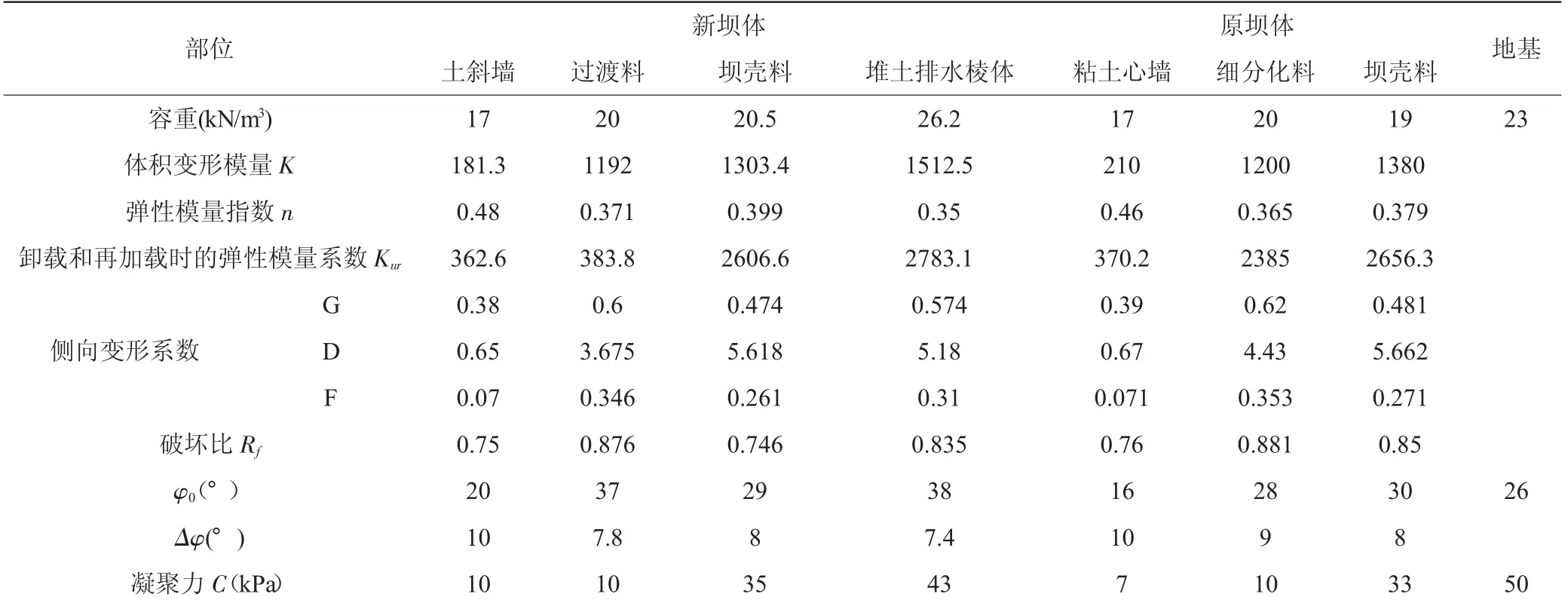
表1 坝体材料参数表(E-μ 模型参数)
对于土石坝,由于土体材料本构为非线性弹性模型,坝体最终的应力变形与加载历史有关。因此,数值分析建模按设计加载顺序分39 级加载,其中第1 级至17 级大坝填筑至1281.88 m 高程(一期填筑),第18 级至39 级大坝填筑至坝顶高层1293.80 m。根据本工程情况,建立的有限元数值模拟计算模型见图2。
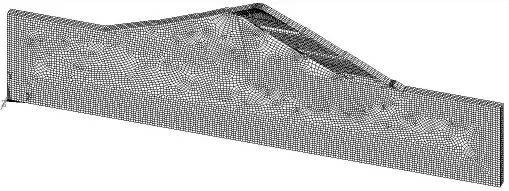
图2 计算模型网格图
4 扩建工程对原坝体的影响分析
4.1 扩建工程对原坝体应力的影响分析
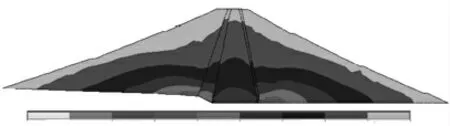
图3 原大坝第一主应力云图
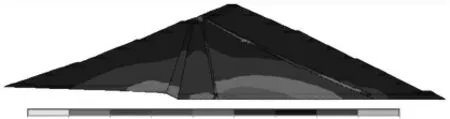
图4 坝体加高后第一主应力云图
图3 表明原坝体最大拉应力为0.03 MPa,位于原坝体上游侧2/3 坝高处。拉应力分布范围极小,仅分布于最大拉应力附近。图4 表明:加高后坝体最大拉应力为0.34 MPa,其最大拉应力位于原坝体下游侧2/3 坝高处,原坝体与新建坝体的过渡区域。通过图3 图4 的对比可以发现,最大拉应力的分布位置和拉应力分布区域的大小发生了变化。相比加高之前只在最大拉应力位置分布有拉应力,其他位置未分布拉应力的情况,坝体加高后拉应力的分布范围发生了变化,扩建后除最大拉应力附近有拉应力分布外,在新老坝过渡区域还分布有其他的拉应力,其分布区域从最大拉应力位置开始,沿着过渡区域向上扩展,一直到新建坝体的斜墙表面。值得注意的是,新建坝体斜墙也出现了拉应力分布,但是其数值极小为2529.72 kPa(图4),不会危及到斜墙的安全。
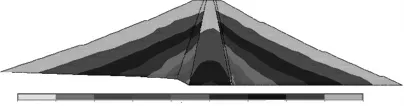
图5 原大坝第三主应力云图
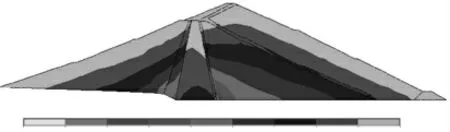
图6 坝体加高后第三主应力云图
图5 表明:加高之前坝体最大压应力为1.58 MPa,位于原坝体心墙下游侧底部;坝体应力以压应力为主,分布于各个部位,上游坝壳、下游坝壳、心墙、坝体均有分布。
图6 表明:到大坝封顶时,坝体最大压应力为2.20 MPa,位于坝体心墙下游侧底部。坝体应力也是以压应力为主,分布于坝体的各个部位。
对比图5、图6 可以看出,大坝最大压应力出现的位置基本相同,加高后最大压应力数值比原来增大约39%,增大幅度较大,其绝对值增加也很大,但是并未超过坝体材料的抗压强度,不会发生危险。
4.2 扩建工程对原心墙应力的影响分析

图7 原心墙第一主应力云图
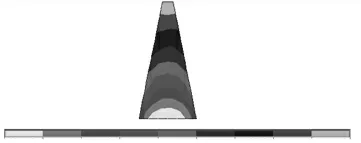
图8 原心墙第三主应力云图
图8 表明:加高之前心墙最大压应力为0.56 MPa,位于心墙底部,应力以压应力为主,图7 表明:未分布有拉应力。

图9 坝体加高后心墙第一主应力云图
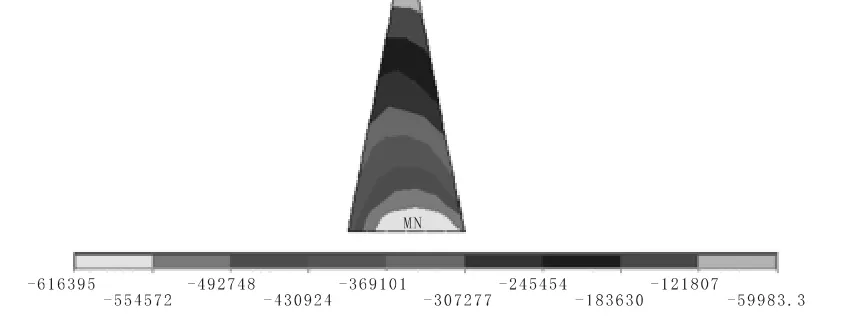
图10 坝体加高后心墙第三主应力云图
新坝体建成后心墙最大压应力为0.62 MPa,位于心墙底部,应力以压应力为主,未分布有拉应力。
心墙最大压应力由0.58 MPa 增大为0.62 MPa,增大约7%,分布位置基本未发生变化。由此可见,坝体加高对原坝体心墙应力没有较大影响
4.3 扩建工程对原坝体位移的影响分析
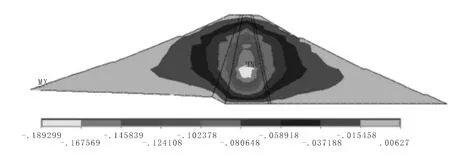
图11 原大坝竖向位移云图
加高前坝体最大竖向位移为18.9 mm,位于坝体中部1/3坝高到1/2 坝高处。
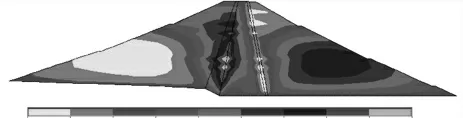
图12 原大坝水平位移云图
加高前坝体最大水平位移为3.3 mm,位于心墙与上游坝体过渡区域。

图13 坝体加高后竖直向位移云图
加高后坝体最大竖向位移为19.7 mm,位于坝体中部1/3坝高到1/2 坝高处。相比原来增大约4.2%。

图14 坝体加高后水平方向位移云图
加高后坝体最大水平位移为5.5 mm,位于心墙与下游坝体的过渡区域。相比原来增大约66.7%。其增大幅度较大,但是原来水平位移的绝对值很小。
大坝的竖向位移在加高前后变化幅度较小,绝对值也比较小;水平位移虽然增大幅度较大,但是原来坝体的水平位移本身极小,所以坝体加高对于原坝体位移的影响不大。
5 结论
基于邓肯- 张E-μ 模型,利用ANSYS 三维有限元软件,对某水库扩建工程大坝计算,进行应力- 应变分析,研究扩建对大坝的影响,结论如下:
(1)原粘土心墙坝坝体最大水平位移为3.3 mm,最大沉降量为18.9 mm,最大压应力为1.58 MPa,最大拉应力为0.03 MPa,水平位移及沉降量分布合理,坝体应力分布符合一般规律。
(2)加高后的坝体最大水平位移为5.5 mm,增大约66.7%,最大沉降量为19.7 mm,增大约4.2%,坝体加高对于原坝体位移的影响不大;最大压应力为2.20 MPa,增大约39%,最大拉应力为0.34 MPa,水平位移及沉降量分布合理,坝体应力分布符合一般规律。坝体不会因为应力的变化出现危险。
(3)加高前、后心墙最大压应力为0.58 MPa、0.62 MPa,增大幅度为7%。加高前后心墙均未出现拉应力,坝体加高对心墙应力的影响不大。
(4)通过对坝体加高前后的应力应变的研究,可以发现,坝体加高不会对大坝整体的稳定性和安全性有较大的影响,且加高后大坝整体变形较小,新建坝体的粘土斜墙上虽出现拉应力,但是其数值极小,斜墙开裂的可能性较小,完建工况下坝体是安全与稳定的。
