基于Cobb-Douglas生产函数的城市工业用水资源边际效益研究

许海东

(辽宁省营口水文局，辽宁 营口 115003)

工业用水边际效益的有效测算是区域水资源优化配置、工业用水水价合理确定的主要依据。当前对于工业用水边际效益的计算大多采用静态方法进行测算[1-5]，但是这种方法对工业用水的技术和规模效率无法进行有效测算，存在一定的局限性。近些年来，基于数学经济模型的动态前沿方法逐步在水资源边际效益测算中得到推广和应用[6-9]，这种方法可以为用水的规模和技术产值等指标进行有效测算，可实现水资源边际效益的有效测算，但是这种方法在工业用水边际效益测算中应用还较少，为此本文引入Cobb-Douglas生产函数，以辽宁某城市为研究实例，基于该方法对城市工业用水的边际效益进行有效测算。

1 Cobb-Douglas生产函数原理

1927年，美国两位学者共同研究出Cobb-Douglas生产函数，该函数的计算方程为：

Y=AKaL1-a

(1)

式中，Y—工业产值万元；A—技术水平；K—工业资本；L—劳动力；a、1-a—资本及劳动对工业产值的贡献度。

水是工业生产不可缺少的主要生产要素，结合水的弹性价格力，进行工业用水水资源边际效益的测算，测算方程为：

Y=AtLaKβWγ

(2)

式中，At—时间变化的动态变量；L—从业人员数量万人；K—工厂的固定资产总额亿元；W—工业用水量亿m3；a—资本弹性系数；β—劳动力弹性系数；γ—用水弹性系数。

将测算方程进行线性化处理，处理后的测算方程为：

lnY=lnAt+alnL+βlnK+γlnW

(3)

将式(3)进行关于W的偏导函数求解，求解方程为：

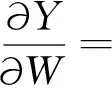
(4)

在具体测算时，还需要对规模弹性影响进行消除，转换方程为：

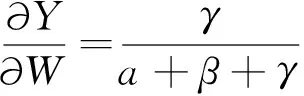
(5)

式(5)中变量同式(2)和式(4)中变量的含义。

2 研究实例

2.1 研究区域工业用水概况

本文以辽宁某城市为研究实例，该城市为辽宁省主要的工业城市，工业万元产值耗水量均值为26m3，万元工业增加值耗水量均值为28m3。城市工业用水情况见表1。近些年来，随着城市供水矛盾日益紧张，工业用水耗水量的优化配置迫在眉睫，急需提高工业用水效率，而工业用水边际效益的精准测算将大大提高城市工业用水的效率，使得工业用水达到最优化。

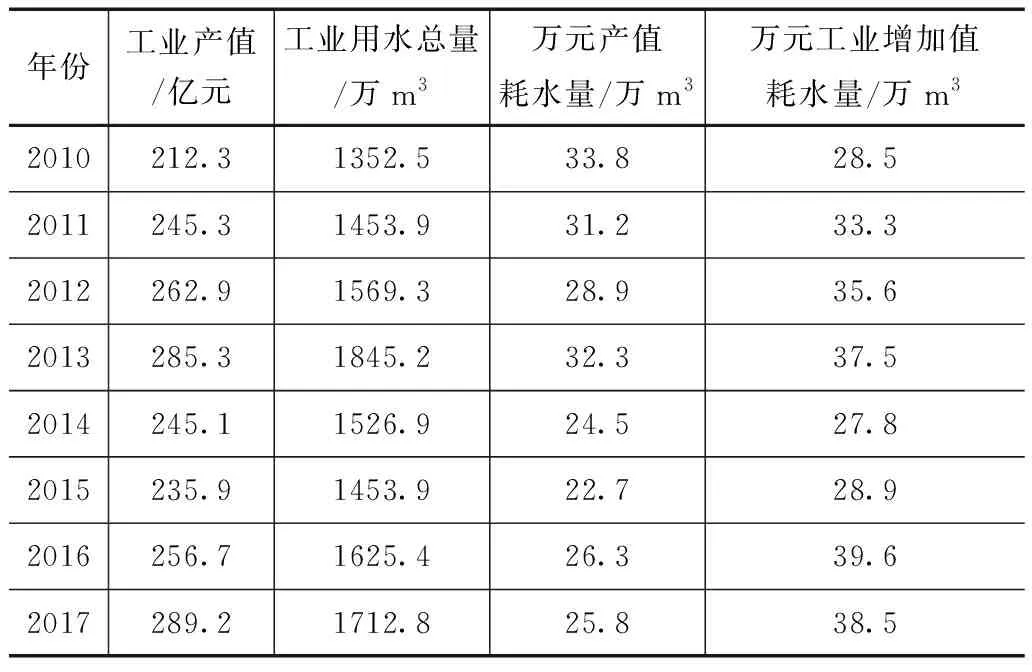
表1 城市工业用水情况

2.2 工业用水动态效率测算

结合城市工业数据，应用Cobb-Douglas生产函数对区域工业用水动态效率进行测算，结果见表2。

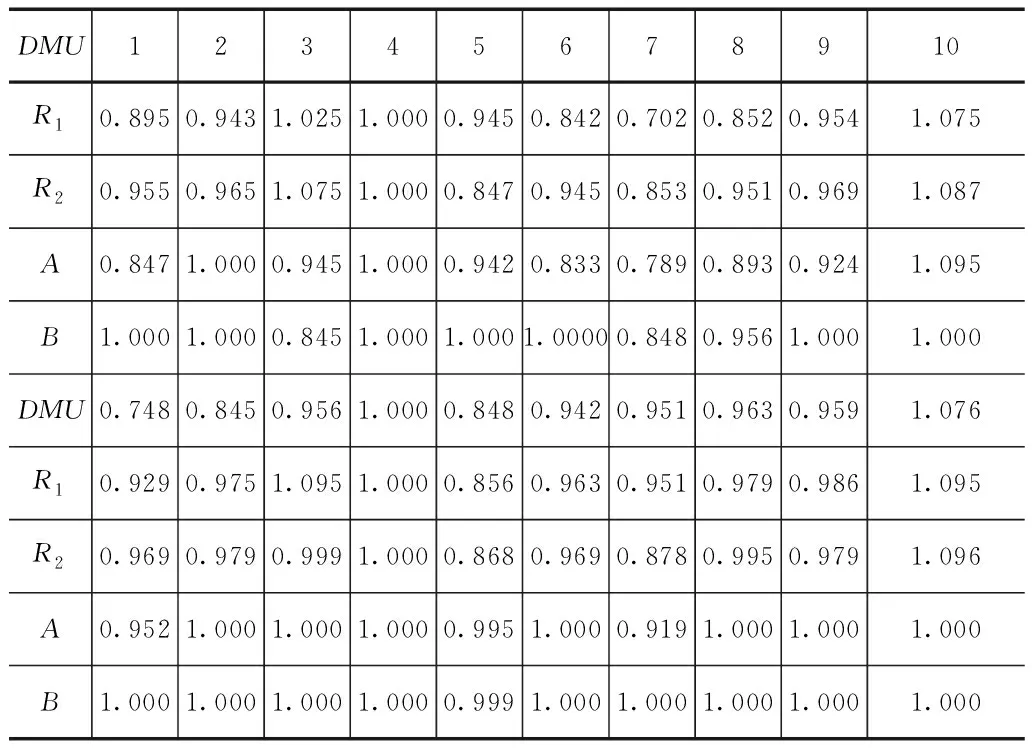
表2 区域工业用水动态效率测算结果

从表2中可看出，区域工业生产的动态效率值在0.702～1.095之间，区域生态效率值总体保持较为稳定，对于效率系数R1和R2而言，效率系数在0.5以上，基本可以满足城市工业用水的边际效益，从表中可看出，区域工业生产用水的边际效益可得到有效满足。从弹性系数A和B可看出。随着循环指标的增多，其弹性系数可以逐步趋近于1.000，模型弹性系数得到优化。

2.3 模型回归系数及回归方程的参数设置

对模型回归系数及回归方程的参数进行设置，设置结果见表3。

表3 模型回归系数及回归参数设置结果

从表3中可看出，Cobb-Douglas生产函数各个参数回归值下95%的上限和下限均可满足方程的精度要求，从标准误差指标可看出，其误差值在0.000～0.008之间，满足方程的标准误差要求，从函数的频率值可看出，其频率值分布在0.000～0.008之间，也同样满足方程的频率分布范围要求。从表中各参数指标的T检验结果可看出，所以参数指标的T检验值均可以满足方程的一致性检验水平。

2.4 工业用水边际效益测算

结合Cobb-Douglas生产函数对区域城市工业用水的边际效益进行测算，测算结果见表4，并将测算结果和实际边际效益进行对比，结果如图1所示。

表4工业用水边际效益测算结果

单元：元/m3

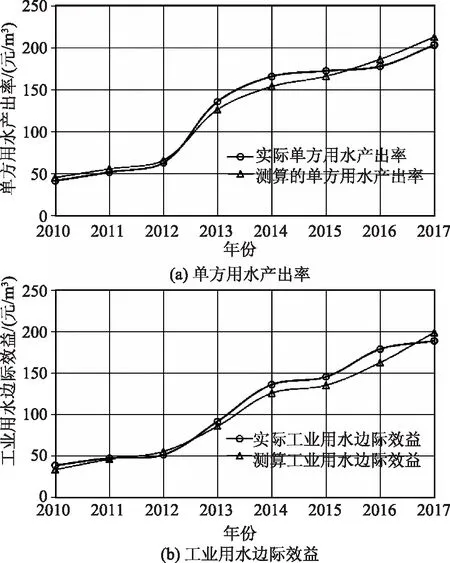
图1 实际工业用水边际效益与测算边际效益对比结果

从表4中可看出，城市工业用水的单方用水产出率和边际效益呈现逐步递增的变化趋势，这主要是因为这些年工业规模的扩大和工业发展，使得城市工业用水的单方用水产出率以及边际效益呈现稳步递增的变化趋势。从图1可以看出，实际单方用水产出率和工业用水边际效益和测算值变化趋势相同，且吻合度较高，表明Cobb-Douglas生产函数在区域工业用水边际效益测算上具有较好的适用性。

2.5 影响因子分析

在区域工业用水边际效益测算的基础上，对工业用水边际效益影响度进行了分析，分析结果见表5、如图2所示。

表5 工业用水边际效益影响度分析结果

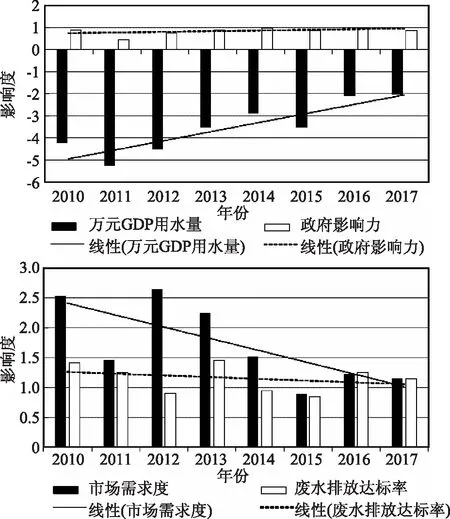
图2 工业用水边际效益影响度分布

从表5中可看出，在4个影响指标中，万元GDP用水量对工业用水的边际效益影响最大，且呈现负向变化的影响，而其他3个指标，对工业用水边际效益的影响均呈现正向变化，这也可从图2中看出，万元GDP用水量的变幅明显要高于其他3个指标。为此需要提高区域工业用水量，需要降低万元GDP用水量，这就需要对区域工业用水结构进行优化，提高工业生产率，从而有效减低万元GDP用水量，降低工业用水边际效益，达到工业用水资源的优化配置。

3 结语

(1)Cobb-Douglas生产函数对城市工业用水边际效益测算精度较高，且数据需求量较少，具有很高的实用性和可操作性。

(2)城市工业用水边际效益呈现递增变化，因改进工业结构，提高用水效率，降低万元GDP用水量，达到工业用水资源的优化配置。

(3)本文在讨论工业用水边际效益时未能对产业规模的影响进行分析，在以后的研究中还需分析产业规模对工业用水边际效益的影响。