基于位姿误差补偿的全电脑凿岩台车钎杆定位算法

夏毅敏，李正光，罗建利，曾桂英，马劼嵩

(1.中南大学 机电工程学院，湖南 长沙，410083；2.中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083；3.中国铁建重工集团有限公司，湖南 长沙，410100)

全电脑凿岩台车是一种集机械、电子、液压等多学科技术于一体的隧道施工设备。与传统凿岩设备相比，全电脑凿岩台车能有效控制超挖量[1]，降低因地质原因引起的施工事故，保障工作人员的施工安全。在施工过程中，关键技术之一是钎杆的快速准确定位。钎杆的自动定位精度和定位速度经常出现不满足工程实际需求的情况，严重影响了隧道施工效率和施工质量。目前，凿岩台车在进行钎杆定位时的研究主要包括运动学误差分析和误差补偿运动学求逆解2部分。近年来，国内外学者对凿岩台车的运动学研究较多，如：JIANG等[2-3]在求解6r-2p凿岩台车的逆解时，为避免求解非线性系统，改变关节输入条件，计算过程不涉及数值迭代和操纵矩阵；WANG等[4]利用对偶四元数法替代DH法进行建模，对六自由度凿岩台车进行逆运动学求解；何清华等[5]建立了多关节钻臂的运动学方程，根据钻臂的实际工作特点和工作范围提出了一种求逆解的方法；周友行等[6]提出了一种基于运动轨迹的求解多关节冗余机器人运动学逆解方法。上述研究均未充分考虑凿岩台车臂架运动学误差的影响，并且未分析存在误差时的逆解计算方法。为此，本文作者借鉴工业机器人运动学误差补偿研究[7-10]和遗传算法在工程中的应用[11-14]，以DH法建立臂架正向运动学模型，通过计算臂架动态误差和静态误差，建立运动学误差补偿模型；在进行钎杆定位时，采用多种群遗传算法，结合无误差补偿运动学逆解结果、移民算子和人工选择算子，计算误差补偿模型逆解，保证凿岩台车钎杆的定位精度和速度。

1 钎杆定位方法

1.1 臂架结构

全电脑凿岩台车臂架包括6个回转关节和2个移动关节，钎杆安装在推进梁上，其主要结构如图1所示。

1.2 钎杆定位方法

影响凿岩台车钎杆位姿误差的主要因素分为动态误差和静态误差，其中，动态误差包括外力、惯性力等导致的弹性变形和振动误差，静态误差包括结构参数误差、环境因素(温度、磨损)导致的尺寸误差和传感器误差等。

在给定钎杆末端位姿情况下，可以根据无误差正向运动学模型求逆解得到对应的关节变量(角度和距离)，并将其作为计算臂架动态误差、静态误差的输入值和钎杆误差补偿模型求逆解的初始搜索值。同时，为保证计算速度和计算精度，预先设定迭代次数，通过MPGA算法对各关节值不断搜索和误差补偿，得到臂架优化关节值，使钎杆达到期望位姿。根据所提的研究思路，对钎杆定位问题进行研究，具体研究路线如图2所示。

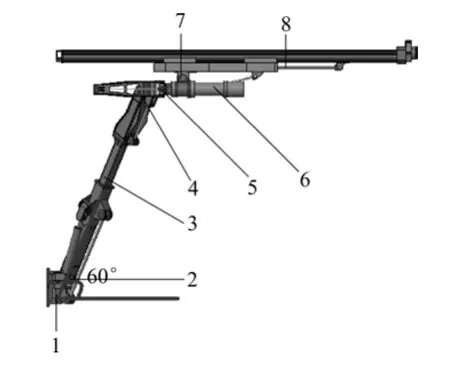
图1 凿岩台车臂架结构图Fig.1 Boom structure of rock-drilling jumbo

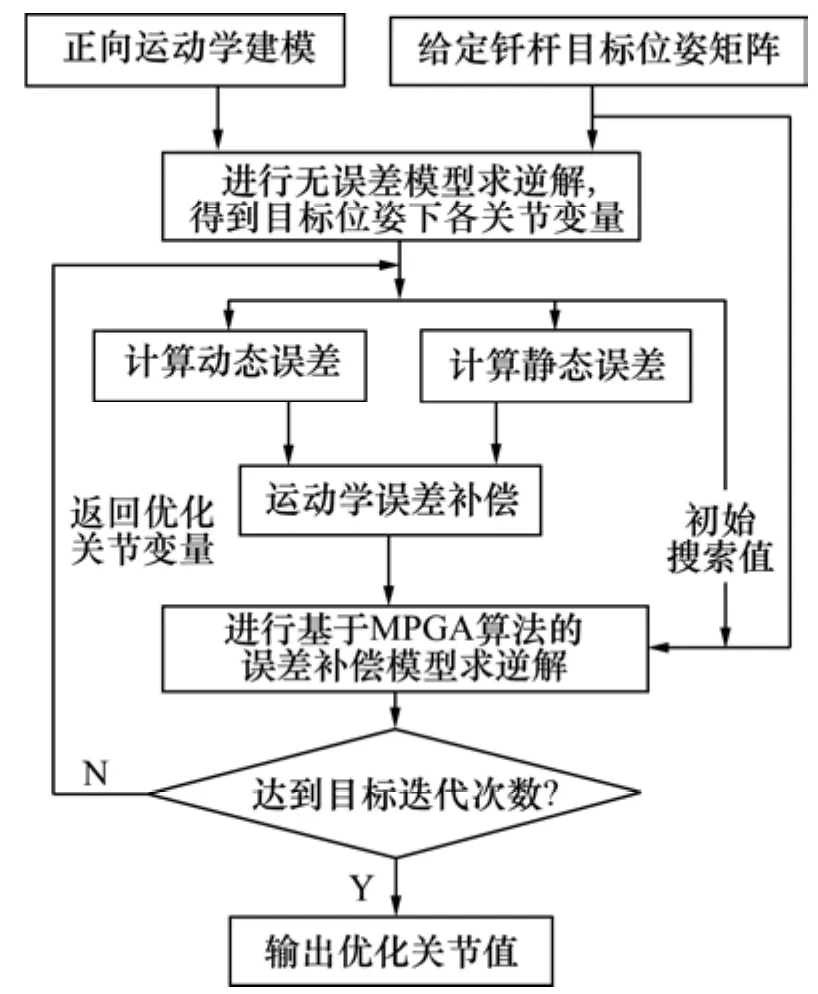
图2 凿岩台车钎杆定位研究Fig.2 Positioning research on drill rod for rock-drilling jumbo

2 钎杆运动学误差补偿模型

2.1 钎杆无误差运动学求解

本文只对锚杆油缸固定的一般工况进行讨论，即锚杆关节为过渡关节，关节角恒为0°。由于DH法属于参数建模方法，坐标系需要建立在关节轴的延长线上，因此，需在不改变运动学结果的前提下对部分坐标系进行位姿变换。根据凿岩台车结构参数，建立各关节坐标系，将推进梁回转坐标系原点o6沿关节轴z6移动距离d6至x7o7z7平面，将锚杆坐标系o7沿关节轴x7移动距离a6至y8o8z8平面。臂架D-H参数如表1所示，臂架运动学模型如图3所示。

图3 钎杆正向运动学模型Fig.3 Forward kinematics model of drill rod

将参数代入关节坐标变换矩阵，得

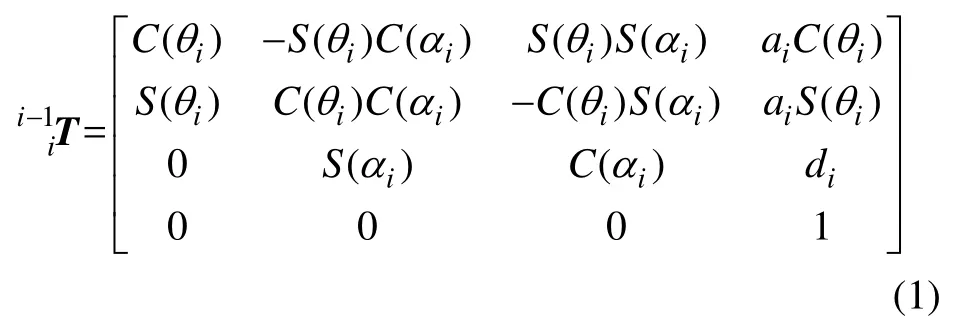
所得臂架正向运动学模型为

式中：i表示第i个关节；C(θi)=cos(θi)；S(θi)=sin(θi)；P=[px,py,pz]，为钎杆位置矩阵；R=[n,o,a]，为钎杆的姿态矩阵。

式中：S24=sin(θ2+θ4) ；C24=cos(θ2+θ4)；Si=sin(θi)；Ci=cos(θi)。在实际施工过程中，为了随时观察凿岩机的工作情况，需要在臂架孔序规划后先确定推进梁回转关节θ6，共0°，90°，180°和270°这4种工况。

根据臂架正向运动学模型进行推导，得

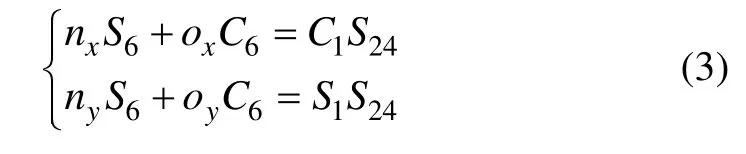
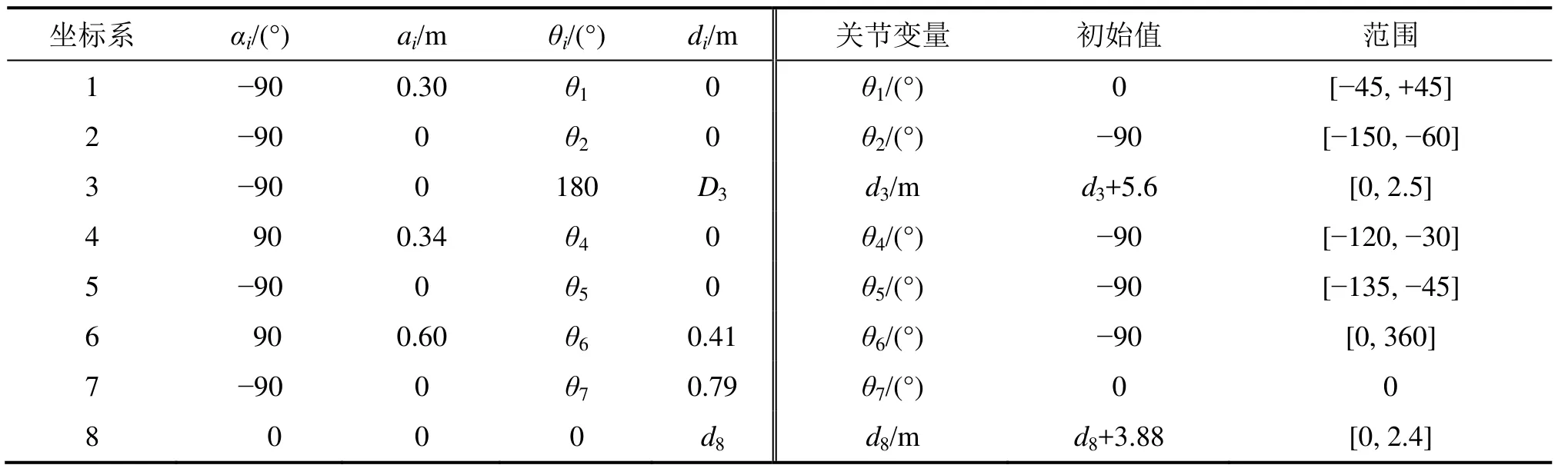
表1 臂架DH参数Table 1 DH parameters of boom

为防止出现分母为0导致计算溢出，将运动学求逆解分为S24≠0的一般工况和S24=0的特殊工况。

2.1.1 一般工况求解

当S24≠0时，

在一般工况下，运动学逆解的求解顺序为θ1→θ5→d8→d3→θ2→θ4。

2.1.2 特殊工况求解

当S24=0时，C24=-1。由于数值解不封闭，有多组解，故先给定大臂伸缩关节d3。

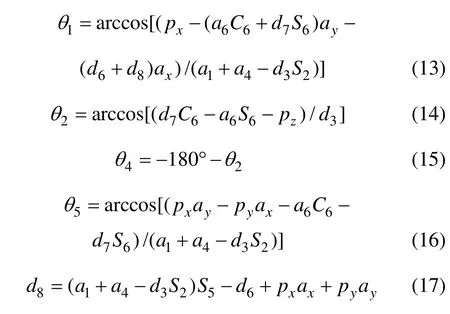
在特殊工况下，运动学逆解的求解顺序为θ2→θ4→θ5→d8→θ1。

2.2 臂架动态误差补偿

2.2.1 大臂及推进梁动态误差计算

将大臂和推进梁分别简化为一端固定的Bernoulli-Euler梁。臂架等效模型如图4所示。由于大臂末端到推进梁的部件总质量超过2 t，大臂末端最大变形达到0.1 m以上，属于大挠度变形，经典挠度公式不再适用，故重新对挠度公式进行改进。

图4 臂架等效模型Fig. 4 Equivalent model of boom

1) 当臂架末端受集中载荷时，臂架任意一点的扭矩为

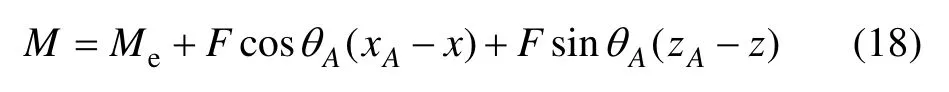
式中：Me为臂架末端所受集中扭矩；F为末端所受集中力。xA和zA分别为末端位置x方向和z方向的位移；θA为转角变形；Me和F受推进梁重心位置影响，其影响参数为大臂俯仰值θ2、推进梁俯仰值θ4和推进梁伸缩值d8。

臂架上任意位置的变形为

式中：z为挠度变形；θ为端截面转角变形；x为轴向变形；E为臂架弹性模量；I为等效转动惯量。

经计算，得到臂架末端角度变形为

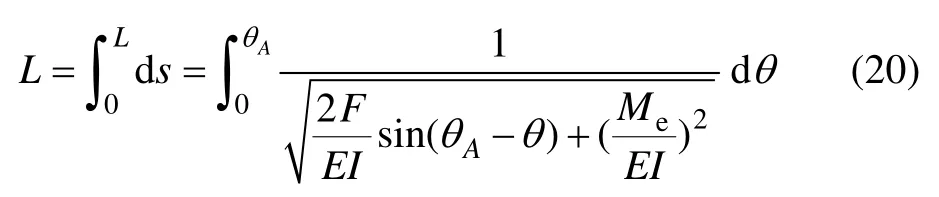
式中：L为臂架的全长。综合式(18)～(20)得

2) 臂架受均布载荷时，根据式(19)，令

代入边界条件s=0，θ=α(其中，α为末端角度变形)，。赋值a0=α，a1=0，得

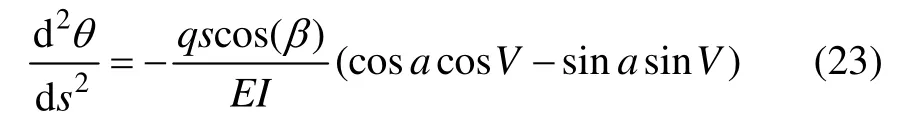
由式(19)得

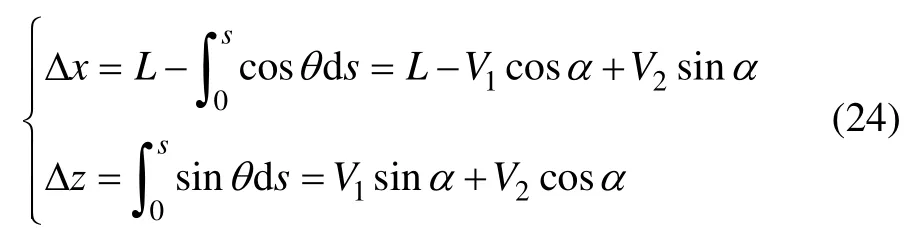
式中：

影响臂架挠度和端截面转角的参数为大臂伸缩值d3、大臂俯仰值θ2、推进梁伸缩值d8和推进梁俯仰值θ4。其中，主要影响参数为大臂俯仰值θ2和大臂伸缩值d3。在旋转关节θ2和移动关节d3的可变范围内对大臂变形求解，设定θ4和d8处于零位，对2种载荷施加方式进行线性叠加，挠度变形Δz和端截面转角Δθ变形结果分别如图5和图6所示。挠度变形Δz分布于0.02～0.12 m之间，端截面转角Δθ分布于0.46°～1.86°之间，变形与大臂长度成正相关。大臂轴向变形 Δx较小，数量级为10-5～10-4，在实际误差补偿中可以忽略。推进梁动态误差规律与大臂的动态误差规律相同，但是数量级过小，在动态误差补偿过程中可忽略。

图5 大臂挠度变形Fig.5 Deflection of large arm

图6 大臂端截面转角Fig.6 Cross rotation angle of large arm

2.2.2 臂架动态误差补偿

对大臂移动关节d3进行动态误差补偿，在进行臂架定位时，基于无误差补偿模型求逆解所得各关节值，进而得到挠度变形Δz和端截面转角Δθ，并将数值代入传递矩阵，变换方式如图7所示。

图7 动态误差补偿坐标变换Fig.7 Coordinate transformation of dynamic error compensation

图7中，坐标系o3先沿x轴移动挠度值Δz，再沿y′轴旋转端截面转角 Δθ，变换至坐标系，进行坐标系传递变换至。变换关系为

式中：TΔ为动态误差补偿矩阵。

2.3 臂架静态误差补偿

基于工业机器人离线标定方法，利用全站仪和角度仪对相邻关节轴进行距离标定和偏转角度标定，修正各关节结构参数(α，a，θ，d)。根据摄动微分理论，对式(1)传递矩阵求偏导，得

2.4 钎杆误差补偿运动学模型建立

结合臂架动态误差和静态误差补偿，得到钎杆运动学误差补偿模型：

3 钎杆误差补偿模型逆解算法

根据钎杆的期望位姿和建立的凿岩台车钎杆运动学误差补偿模型，采用多种群遗传算法(MPGA)对误差补偿模型求逆解，对各关节变量不断搜索和误差补偿，计算各关节优化值，使钎杆达到期望位姿。

3.1 钎杆运动学MPGA模型

3.1.1 构造初始种群

初始种群为MPGA算法的搜索出发点。本文构造的初始种群数为10个，每个种群个体数为100个。设定每个关节值在个体的染色体中占据20个基因位置，保证算法的求解精度。

3.1.2 构造目标函数

已知钎杆期望位姿为

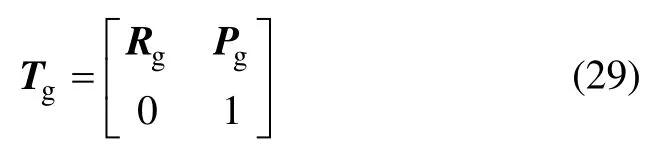
式中：Rg为钎杆期望姿态矩阵；Pg为期望位置矩阵。

将种群中各个个体的关节值代入臂架运动学误差补偿模型，得到个体的当前钎杆位姿矩阵：

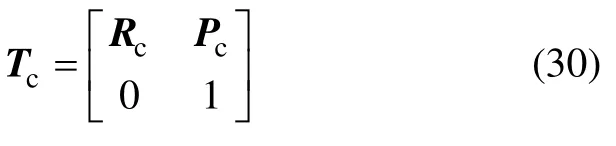
式中：Rc为钎杆当前姿态矩阵；Pc为当前位置矩阵。

构造目标函数：

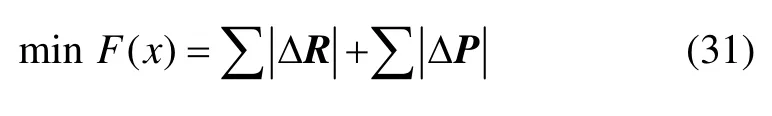
式中：ΔR=Rg-Rc，为各种群中个体的钎杆计算姿态和期望姿态的姿态误差； ΔP=Pg-Pc，为钎杆计算位置和期望位置的位置误差。

3.1.3 设计约束条件

根据正向运动学求逆结果，将各旋转关节角范围缩减为θi±10°，将各移动关节距离范围缩减为di±0.2 m，优化了各关节变量的搜索范围，提高了算法的求解速度。

交叉率Pc决定了遗传算法的全局搜索能力，传统交叉率Pc取值范围为0.7～0.9。MPGA采用多点交叉方式，增强了算法搜索能力，避免早熟收敛。

变异率Pm决定了局部搜索能力，传统Pm取值范围为0.001～0.050。由于搜索范围已经相对减小，需要增强局部搜索能力，因此，变异率Pm相对增大，取Pm为0.05。

3.1.4 构造适应度函数

采用轮盘赌法选择适应度高的个体进入下一代，构造适应度函数F为

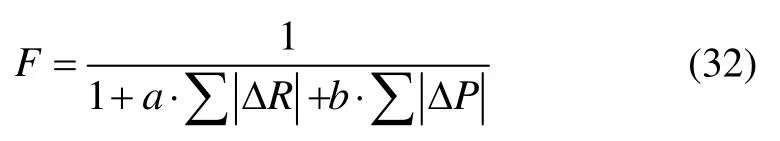
式中：a和b分别为姿态误差和位置误差的权重系数。姿态参数单位为 rad，位置参数单位为 m，两者数量级相同。经过大量测试确定权重系数为a=1，b=1.5～2.5。

3.1.5 优化方案

采用移民算子，打破各种群的独立性，将各种群的最优个体引入其他种群，替代其他种群中的最劣个体，实现各种群协同进化。

采用人工选择算子，将每代中最优个体放入精华种群，精华种群不进行选择、交叉和变异等操作，只记录和更新每一代最优种群。

3.2 求解精度分析

给定一组关节值(θ1=20°，θ2=-45°，d3=0.4 m，θ4=-15°，θ5=0°，d8=2.0 m)，推进梁回转关节角θ6和锚杆关节角θ7为0°，采用MATLAB进行算法编程，基于运动学误差补偿模型所得到的钎杆位姿计算 20次逆解。对比计算关节值和给定关节值相对误差平均值，结果如表2所示。旋转关节的相对误差远小于移动关节的相对误差，两者相差1个数量级。这是因为凿岩台车结构尺寸较大，旋转关节对位姿误差的影响要远大于移动关节的影响。大臂伸缩关节d3和推进梁伸缩关节d8具有明显互补关系，可以适当提高适应度函数中位置误差的权重系数b，增大移动关节对末端位姿的影响。

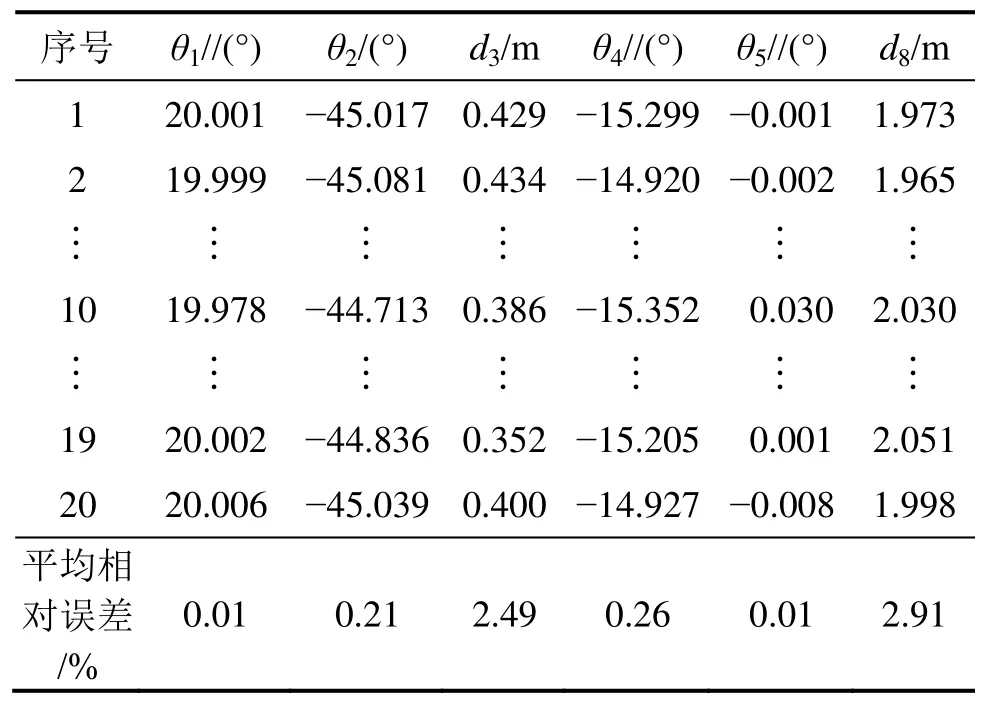
表2 逆解计算关节值及相对误差平均值Table 2 Inverse calculation of joint value and average relative error value

分别选取算法中最快和最慢种群的进化过程进行对比，结果如图8所示。MPGA算法在400代内使适应度达到0.99以上，求解能力强，收敛速度快，计算结果稳定可靠，不会发生早熟收敛现象。因此，将算法结束条件设置为计算到第400代种群。

4 试验验证

图8 MPGA遗传算法进化曲线Fig.8 Evolution curves of MPGA genetic algorithm

图9 隧道炮眼图Fig.9 Borehole of tunnel

根据凿岩台车施工时的实际停车位置和炮眼设计，给定18组凿岩台车钎杆期望位姿值，期望位姿如图9所示。其中，圆点位置代表钎杆定位位置，其上引出的线段为钎杆需要达到的姿态在掌子面上的投影。设定直径为11 m级隧道掌子面距离凿岩台车大臂横摆中心距离为12 m，图示坐标系水平向左为y轴，竖直向上为z轴，垂直掌子面向里为x轴。进行基于误差补偿模型的逆运动学求解，得到各关节对应数值。在车间使用全站仪于大臂横摆中心设站，驱动臂架各关节至计算关节变量，利用全站仪测量钎杆位置，测量结果如表3所示(其中，[x,y,z]为期望坐标，为臂架移动后的钎杆实际坐标)。

表3 钎杆测量结果Table 3 Measuring results of drill rod

对比测试位置与期望位置的位置误差，结果如图10所示。从图10可见：x方向平均误差为0.031 m，y方向平均误差为0.028 m，z方向平均误差为0.029 m，总距离平均误差为 0.056 m，并且总距离误差均小于0.100 m，满足工程实际定位要求。

图10 钎杆末端位置误差Fig.10 End position errors of drill rod

5 结论

1) 臂架负载和自重产生的动态误差不容忽略，大臂挠度变形范围为 0.04～0.12 m，端截面转角范围为0.46°～1.86°；轴向变形数量级为10-5～10-4，变形较小。推进梁的动态误差规律与大臂的动态误差规律相同。

2) 针对工程中全电脑凿岩台车钎杆快速定位问题，提出了一种基于运动学误差补偿模型和MPGA算法求逆解的钎杆定位方法，根据无误差正向运动学逆解结果优化各关节变量的搜索范围，结合移民算子和人工选择算子，提高算法的求解速度和收敛精度，得到给定位姿下的优化关节变量。

3) 在车间对全电脑凿岩台车进行钎杆定位试验，根据钎杆期望位姿矩阵求逆解得到优化关节变量，驱动臂架各关节至对应关节变量，实测钎杆位置与期望位姿值误差小于0.100 m，满足工程实际定位要求。