沪深300指数价格波动的集聚性分析
2019-02-20刘艳华
陈 玲 刘艳华
(安徽工业大学,安徽 马鞍山 243000)
一、引言
股票作为一种高风险高收益特征的有价证券,其价格的波动一般体现在收盘价上,而根据收盘价的连续变化则可反映出股票收益的波动,进而得出收益率的时间序列。现实中,由于买卖双方的连续竞价,致使股票收益的变化趋势在一段时间内相对一致,此现象在学术文献中又被称为 “波动性集聚”(volatility clustering)或“扎堆”。波动性集聚的现象往往来于外部对股价波动的冲击性持续影响,其反映在股票收益率的正态分布图中最为明显的特征是“尖峰厚尾”。除此之外,对于股票价格波动特征的分析,学术界也提出了几点论证:一是通过时间序列收益率的趋势分析,其是否存在波动集聚现象;二是收益率的峰顶正态密度值与左尾部概率与理论值相比较是否较高;三是其模型扰动项是否拒绝正态分布且其残差是否存在ARCH效应;四是其残差平方项是否存在高阶自相关现象。
沪深300指数是反映我国普通股股票价格波动的一个代表性指标,其价格的波动不仅反映大盘的风险收益状况,更会对我国股民手中普通股产生深刻影响,究竟其价格波动是否存在暴涨暴跌现象是值得探究的。因此,本文根据近三年沪深300指数的日收益率通过建立ARMA模型初步判断其波动情况,进而通过GARCH模型深入分析和预测,发现我国普通股股票市场确实存在波动集聚现象,且其集聚行为短期内对普通股股票价格影响较为显著,而随着时间的推移,其影响逐渐减弱。
二、文献综述
沪深300指数是反映我国普通股股票市场的一种综合性指标,其存在大概覆盖了我国60%普通股股票的市值。关于沪深300指数收益率的波动,引起了国内学者的关注和探讨。
(一)收益率波动的分析方法
现有文献中衡量股票价格波动最常用的指标是其收益率,其中可分为高频和低频收益率,由于低频收益率拟合和预测股票价格波动效果存在一定的误差,因此一般使用日收益率和间隔分钟收益率进行衡量。而随着计量方法的发展和完善,目前对股票收益率波动特征分析的有 ARCH (鲍松杰,2017[1])、GARCH(尹智超,2013[2])、TARCH(马国腾,2010[3])、EGARCH(康凯,2017[4])以及有偏的 GED-GARCH(王喆,2018[5])等模型,其中使用较多是GARCH族模型。
(二)收益率的波动特征
经过对其指数收益率的波动分析发现,主要存在以下特征:波动集聚性(卞昕华,2015[6])、尖峰厚尾性(王海波,2015[7])、非正态性(冷军,2012[8])以及杠杆性(尹智超,2013)[2]在影响因素方面,吴灿(2014)利用SPSS软件对影响收益率波动的换手率、成交量、市场收益率进行了研究,发现其影响较为显著[9]。此外,胡龙(2013)创新和利用了RV-MSM模型对其收益率的波动进行了拟合和预测,并进一步丰富了市场的微观结构对其的影响[10]。
目前,国内学者对沪深300指数收益率的波动研究较为丰富,其采用的计量模型也日益先进,其中拟合优度使用较多且较好的主要是GARCH族模型,而与ARMA模型结合进行分析和预测的较少。因此,本文将根据2016年1月4日至2019年6月3日高频数据利用两种模型对沪深300指数的价格波动进行了分析和预测,以探析其价格波动是否存在暴涨暴铁现象。
三、研究方法
(一)ARMA—GARCH模型概述
1.自回归滑动平均模型(简称ARMA模型),是一种适用于平稳时间序列分析的计量方法,其主要通过判断时间序列的自相关图与偏自相关图,进而建立相应的AR模型、MA模型或者ARMA模型,它主要反映的是时间序列的结构和特征,进而得出整个序列的规律性。ARMA模型表达式为:

其中{εt}是白噪声序列,r和s都是非负整数,简记为 ARMA(r,s)。
2.广义自回归条件异方差模型(简称GARCH模型)在现有文献中常被用来研究金融价格波动的特征的一种ARCH效应的拓展模型,其主要在ARMA模型建立的基础上对其扰动项方差的稳定性进行分析和预测,以判断其扰动项的平方是否存在异方差,其涉及的表达式为:

r和 s都是非负整数,简记为 GARCH(r,s)。
(二)样本数据的选取和计算
本文根据东方财富网选取了沪深300指数近三年(2016年1月4日至2019年6月3日)的日收盘价作为其计算价格波动指标,进而根据公式:计算出日收益率以反映其价格波动情况,其中It代表沪深300指数第t日的收盘价,相对应的It-1为前一日的收盘价,共计831个数据,实证分析主要是通过stata软件进行完成。
四、实证分析
(一)沪深300指数价格波动的集聚分析及ARMA模型的建立
1.收益率的基本特征分析以及平稳性检验
首先对价格波动的日收益率序列{}进行趋势性分析,分析结果如图1:

图1 收益率的基本趋势性分析
从图1日收益率的趋势分析可以看出,其波动基本围绕均值波动,且呈现上下频繁波动的状态,反映出沪深300指数近三年的价格波动不仅呈现出持续性的偏高或偏低现象即“波动性集聚”现象。为了进一步判断其平稳性,对其进行有常数项而无趋势项DF检验,检验结果见表1。

表1 收益率的单位根检验
从表1可以看出,其收益率DF统计量值-31.563分别小于1%临界值-3.43、5%临界值-2.86以及10%临界值的-2.57,根据计量统计原则,可以判断其收益率序列不存在单位根现象,是平稳序列。
2.收益率ARMA模型的选择和建立
时间序列的自相关与偏自相关图是ARMA模型建立的基础。因此,本文首先对其价格波动的日收益率建立其相应的自相关和偏自相关图,如2和图3:

图2 收益率的自相关图

图3 收益率的偏自相关图
从图2和3可以看出,无论是自相关图还是偏自相关图在第三阶均落在95%的置信区间外,表明其在5%的显著水平下不为零,同时3阶以上的自相关与偏自相关系数均为0。因此,本文根据自相关系数与偏自相关系数断尾情况,分别考虑建立AR(3)与 MA(3)模型。首先,估计 AR(3)模型(见表 2)。

表2 收益率AR模型的建立
根据表2可以看出,在P值5%的显著水平下,其 AR(1)与 AR(3)模型是显著的,接下来对其残差项检验是否存在自相关,若不存在自相关现象,表明适合建立AR模型(见表3)。

表3 收益率AR模型的残差项检验
表3显示,其收益率残差项的P值均大于5%显著水平,即接受不存在自相关的原假设,从而表明可以建立AR(3)模型。
其次,对收益率估计 MA(3)模型(见表 4)。

表4 收益率MA模型的建立
由表4可知,在P值5%的显著水平下,其MA(1)与MA(3)模型是显著的,接下来依旧对其残差项检验是否存在自相关(见表5)。

表5 收益率MA模型的残差检验
由表5,可以发现其MA(3)模型中残差项的P值在5%的水平下均显著,即接受不存在自相关的原假设,从而表明可以建立MA(3)模型。
根据上文 AR(3)模型与 MA(3)模型的估计,发现其两个模型中的第二阶系数均不显著,为了考虑更为简洁的模型,下文将省去第二阶变量并根据信息准选择更合适的模型(见表6)。

表6 模型信息准则
根据信息最小准则发现:其AR(3)模型比MA(3)模型更为合适,且由于 AR(2)模型不显著,因此省去第二阶的AR(3)模型更为合适,为此本文对沪深300指数收益率建立AR(3)模型(见表7)。

表7 收益率的AR(3)模型的建立
因此,根据上表其收益率的AR(3)模型的表达式为:

(二)沪深300指数价格波动收益率的ARCH效应检验及GARCH模型的建立
1.收益率分布的正态性检验
关于股票收益率的波动性集聚现象最为明显的特征是“尖峰厚尾”,为了进一步验证其收益率的峰顶密度与左尾部概率究竟是否高于理论值,本文需建立相应的正态分布图(见图4)。
根据图4的正态检验可以看出,其价格波动日收益率的峰顶不仅高于理论正态分布图中的峰顶且其形状也呈现出“刀刃”形态,进一步观察发现其左端的分布概率要显然高于右边,最终呈现出“尖峰厚尾”的特征。表明沪深300指数价格波动的日收益率并不服从正态分布。
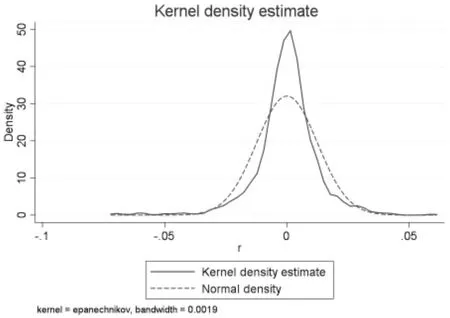
图4 收益率的核密度与正态密度
下面对其扰动性的正态性进行严格的统计性检验(见表 8)。

表8 收益率扰动项的正态性统计检验
通过对其收益率扰动项的正态性统计检验可以看出,无论是 Skewness test还是 Kurtosis test其统计量的P值在chi2的基础上均为0,表明收益率的扰动项根本不服从正态分布,即不满足同方差的条件而存在异方差。当扰动项存在异方差时,可初步判断其存在ARCH效应。因此,本文将对其扰动项的平方进一步进行LM检验(见表9)。

表9 收益率残差平方的ARCH效应检验
2.收益率残差平方序列的ARCH效应的检验
根据日收益率残差平方项的ARCH效应检验可以看出,其在滞后一阶是不存在ARCH效应的,而在滞后二阶和三阶其P值为0,强烈拒绝不存在ARCH效应的原假设(即拒绝服从正态分布),表明其扰动项不仅存在ARCH效应,而且是高阶。除此之外,若价格波动日收益率存在高阶自相关,则可进一步建立GARCH模型进行分析和预测。
下面,通过进一步检验其残差平方项是否存在自相关现象(见表10)。

表10 收益率残差平方项的自相关检验
根据表10,其收益率的残差平方项在滞后一阶时,其不存在自相关现象,而滞后二阶至八阶其残差平方项不但存在自相关现象,且随着阶数的增加,自相关系数、偏自相关系数以及Q检验,依然拒绝原假设,表明其收益率的残差平方项实际存在高阶自相关现象。
3.收益率GARCH模型的建立和预测
由于收益率的残差平方项是一个高阶自相关序列,在对其建立GARCH模型之前,需根据信息准则判断ARCH模型的回归阶数,进行确定建立相应GARCH模型(见表11)。
根据表11信息准则(*号多)显示,其残差平方项在滞后四阶*号最多,为此应对残差平方序列建立 ARCH(4)模型(见表 12)。
表12ARCH(4)模型的显示,其所有的ARCH项均很显著,故假设其服从统计学中的t分布。一般一个高阶的ARCH模型,只需建立一个低阶的GARCH(1,1)模型即可满足预测。
通过表13可以看出:无论是ARCH项还是GARCH项均在5%水平下显著。因此本文根据表7与表10建立的AR-GARCH模型为:

最后,利用GARCH(1,1)模型对其日收益率条件方差进行预测(见图5)。
通过图5可以发现,其价格波动日收益率的条件方差,在短期内受波动集聚的影响较为剧烈,而随着时间的推移,其影响逐渐减弱。

表11 收益率残差平方序列的自回归阶数

表12 收益率ARCH(4)模型的建立

表13 收益率残差平方序列的GARCH(1,1)模型

图5 条件方差的时间趋势
五、结论
通过对沪深300指数近三年价格波动日收益率的分析可以发现,其不仅拒绝正态分布的理论假设,且其在正态检验中又呈现出“尖峰厚尾”的特征。此外其残差扰动项不但存在高阶ARCH效应且其平方项亦存在高阶自相关现象。上述现象表明我国沪深300指数价格波动不仅存在波动集聚现象,且通过建立AR模型与GARCH模型对其波动性进行了拟合和预测,结果表明沪深300指数收益率的波动仍然存在暴涨暴铁的现象,这表明我国目前的普通股股票市场仍然不是一个成熟的市场,易受到外界环境的冲击和影响。此外,我国管理层应加强对股市规范管理,切实根据股市情况实行相应的政策,从而更好地发挥调节我国股市的适应能力,以维持金融市场的稳定。
