基于3DEC模拟的既有铁路单体滑坡危险性分区与评价
——以川黔线裁缝岩滑坡为例
2019-02-20李嘉雨毛邦燕葛云峰
李嘉雨 毛邦燕 陈 亮 葛云峰 王 栋
(1.中铁二院劳模(专家)地质创新工作室,四川成都 610031;2.中铁二院工程集团有限责任公司,四川成都 610031;3.中国地质大学(武汉)工程学院,湖北武汉 430074)
西南险峻山区铁路沿线滑坡灾害分布广泛,据统计,1978年发生在铁路上的滑坡、崩塌约有1 700处。多年来,平均每年因滑坡导致既有铁路中断运输44次,中断行车时长800 h以上,造成的直接经济损失达数千万元[1]。以下两个方面的原因使我国铁路沿线依旧面临着严重的滑坡地质灾害:①受原有勘察手段和投资额度的限制,既有铁路未完全绕避的滑坡;②受自然因素或人类工程活动影响,铁路沿线一些潜在不稳定斜坡逐渐演变形成新的滑坡体。
单体滑坡危险性评价通常包含三个要素:在一定时间内发生的可能性、滑移距离和滑移速度[2]。国外学者对崩滑体的危险性研究开展较早,在区域性滑坡的危险性评价方面有着丰富的经验,但对单体滑坡危险性评价的研究较少。Bunce等[3]通过记录公路沿线崩塌的发生频率来评价公路危岩落石的危险性,并首次将危险性的概念引入到地质灾害评价中。T Glade[4]认为滑坡的历史数据在滑坡危险性评价中有重要的作用。Cardinali M等[5]运用多期航拍数据解译、现场调查、滑坡库存地图等地貌学的方法评估意大利中部翁布里亚区域的滑坡危险性和风险性。William等[6]将一阶、二阶矩(FOSM)近似极限平衡边坡稳定性方程与数字高程模型相结合,在美国西维吉尼亚州Wheeling地区开展了基于空间分布概率的滑坡危险性分析。Rex等[7]介绍了美国使用激光雷达、物理模型和三维斜坡-稳定性模型(SCOOPS)在西雅图地区开展滑坡危险性评价的进展。
而国内学者对滑坡危险性评价研究起步较晚,但发展较快,尤其是针对单体滑坡的危险性风险评价进行了许多有益的工作。陈丽霞等[8]采用Monte-Carlo方法预测了滑坡发生的概率,并利用能量守恒原理和谢德格尔公式,结合滑坡裂缝的展布方位,预测了滑坡灾害发生后的影响范围。张茂省等[9]利用滑坡风险评价与管理理论对延安市虎头峁滑坡进行了危险性及社会风险评价;韩金良等[10]通过斜坡失稳概率计算和滑坡事件统计分析评价经验公式两种方法,对吴家沟滑坡进行了地质灾害风险评估。唐亚明等[11]进一步总结了一种以高精度数字高程模型(DEM)和Quick Bird遥感数据为调查基础的大比例风险区划和评价方法。薛强等[12]提出了基于多期三维数值高程模型(DEM)和滑坡强度的单体滑坡危险性定量评估方法。冯立等[13]对不同降雨工况下的四川虹口黑泥湾滑坡开展了风险性评估和风险区划。这些研究为当地的滑坡风险评估与管理提供了技术支撑,并取得了显著的经济效益。
总结目前国内外研究现状,单体滑坡滑距预测及评价方法有四种:地貌学方法、几何学方法、经验模型法、碎屑流的变体积法。可行的滑坡强度预测方法有三种:数学模型法、数值模拟法和位移速率监测法。时间概率预测及评价的方法有两种:“直接利用编录过去已发生的滑坡事件”、“间接利用触发因素重现周期信息”[14]。
铁路工程呈线性展布,沿线滑坡点具有工程地质条件多变、地质灾害零星发育等特点。根据以上特点,既有铁路单体滑坡难以根据“编录已发生的滑坡事件”或经验公式来评价。随着数值模拟技术的发展成熟,使通过数值模拟法来预测滑距和滑坡强度,快速识别滑坡失稳后的运动路径和影响范围成为可能。
早在2008年,滑坡和工程边坡联合技术委员会(JTC)就提出了采用数值模拟的方法来模拟评价滑坡运动距离和速率的建议[15]。在国外,Fall等[16]将二维有限元和离散元方法用于区域滑坡危险性分区;而在国内,吴钟腾[17]利用土工离心机和3DEC数值模拟手段对麻窝滑坡的运动危险性进行了验证分析。目前,借助数值模拟的手段开展单体滑坡的危险性分区和评价的国内外学者还较少,在铁路上的应用更是空白。
以川黔线裁缝岩滑坡为背景,在前期对滑坡基本特征和形成机理认识的基础上[2],利用3DEC模拟滑坡体大变形、旋转和运动,预测裁缝岩滑坡再次失稳后的运动路径、滑动速率及影响范围;利用模拟结果结合层次分析法制作了危险性分区云图;利用触发因素(3日降雨量阈值)的年概率获得了滑坡的失稳概率。以上成果可为裁缝岩滑坡风险评估与管理、灾害的治理与人员搬迁安置提供理论依据,同时也为西南险峻山区既有铁路滑坡灾害风险评价与管理提供了借鉴。

图1 裁缝岩滑坡无人机航拍全景
1 裁缝岩滑坡概况
裁缝岩滑坡所在区域(见图1)地貌属浅中切割侵蚀-构造中低山;滑坡位于官田寺背斜的北西翼,为单斜构造;滑坡区主要出露地层有:第四系全新统坡残积层、滑坡堆积体、崩坡积层,侏罗系中统上沙溪庙组。
滑坡长460 m,宽90~100 m,整体呈不规则四边形,平均厚度约5~20 m,总方量为162×104m3。滑体后部以岩体滑动为主,下伏基岩为侏罗系沙溪庙组二段紫红色中厚层-厚层泥岩夹灰白色中厚层砂岩,产状320°∠20°,发育两组优势结构面(JL1、JL2),产状分别为182°∠75°和55°∠82°(见图2);中前部为土体滑动,主要为第四系滑坡松散堆积物粉质黏土夹碎石(见图3)。

图2 后缘滑坡壁
滑体前部临空,中部平缓,后部陡斜;斜坡沿南侧临空面崩塌剥蚀且岩层倾向北西,使滑体北侧厚,南侧薄。根据滑坡的变形特征,可将滑坡划分为主滑区、剪切挤压区。其中,主滑区又可以分为启动推移区、挤压下错区、鼓胀滑塌区(见图4)。滑坡区内地表水主要以大气降水补给为主,通过无人机航拍解译及调查,滑坡壁后部存在3条季节性水沟,在滑坡后缘易形成点状入渗的季节性基岩裂隙水,并沿滑带流动至前缘鼓胀滑塌区,最后以泉的形式沿坡脚岩层面渗出,排泄于冲沟。

图3 滑坡前缘剪出口

图4 裁缝岩滑坡2-2′纵剖面
前期调查研究表明:该滑坡是在自重应力的牵引作用以及降雨入渗至后缘的张拉裂缝而使滑带泥化软化,最终诱发失稳破坏。
2 滑坡的危险性分析
2.1 滑坡的稳定性分析

图5 滑坡监测点的变形(降雨量)-时间曲线
滑坡失稳后,采用全站仪对滑坡的变形位移开展了应急监测(见图5)。在47 d内,DMP1累计变形量为-2.9 mm,DMP2累计变形量为-36.3 mm,DMP3累计变形量为3.7 mm,DMP4累计变形量为-42.4 mm,DMP5累计变形量为-4.3 mm。监测结果表明:滑坡左侧边界的变形量大于滑坡右侧边界的变形量;滑坡后缘的变形量大于前缘的变形量。
由传递系数法,滑坡1-1′,2-2′,3-3′三个纵剖面(见图1)暴雨工况稳定性系数分别为0.47,0.48,0.79,皆处于不稳定状态。
综合以上分析,该滑坡完全失稳后,滑带完全贯通,抗剪强度大幅降低,在暴雨条件下饱水软化,仍然有进一步失稳滑动的可能性。为了快速准确地评价滑坡失稳对川黔线雷吼洞洞口及前缘居民区的影响,运用3DEC离散元软件模拟滑坡再次失稳后的滑动范围及速率,并进行危险性分区和评价。
2.2 地质模型的建立与参数的选取
滑坡模型长800 m,宽630 m,高约263 m;设定模型的z方向为重力方向,x方向为正东方向(指向山体内部),y方向为正北方向。滑坡模型x、y方向和z方向底面为约束边界。根据实际情况划分为主滑区(3、4、5号区域)、剪切挤压区(2号区域)、下伏基岩(1号区域)三部分(见图6)。

图6 裁缝岩滑坡模型
模型滑面为岩层层面,采用3DEC莫尔-库仑模型开展计算。滑体后部为松散的岩体,主要发育两组优势结构面(JL1、JL2),故对后部滑体按照岩层层面和两组优势结构面进行切割。中前缘碎石土在空间上都是离散的块体,如果将其考虑为一个整体,则块体间无法分离。因此,将中前缘滑体也切割成细小的块体来模拟碎石土离散的力学特征。块体间的力学性质采用节理面接触-库伦滑移模型计算,并在滑坡上设置7个监测点(见图7),以获得滑坡不同部位的滑动距离和滑速。
由实际监测数据可知(见图5),滑坡滑带逐步泥化、软化,进而产生变形。模拟计算时,3号区域的滑带首先软化,待滑坡位移稳定后,4、5号区域的滑带依次软化直到滑坡完全失稳。为计算滑坡失稳后破坏的最大范围,主滑区滑带按暴雨工况下处于饱和状态考虑,故取滑带土液限饱和状态下的物理力学参数(见表1);受冲沟的排水作用,剪切挤压区滑带未处于饱水状态,故剪切挤压区块体间依照滑带土天然力学强度计算(见表1);下伏基岩为不可变形的刚体。

图7 滑坡模型监测点分布

表1 裁缝岩滑坡岩土体物理力学参数
2.3 危险性模拟结果与分析
当滑带处于天然状态下时,数值模拟计算结果显示滑坡体发生微量变形后趋于稳定,这与滑坡的实际情况相符。
当3号区域(见图6)滑带软化后,滑体后缘形成约5 m宽的后缘拉裂缝,主滑区前缘局部滑塌,而后部趋于稳定。当3、4号区域(见图6)滑带均软化后,滑坡立刻失稳破坏,主滑前缘首先剪出。考虑到滑坡失稳后的运动时间远远小于降雨入渗至5号区域的时间,故5号区域滑带的力学参数仍按照天然状态下的力学参数考虑。而后,由于滑坡前缘5号区域对后缘滑体的阻挡作用,使滑坡左侧中部部分滑体沿左侧陡坡下滑并形成溜滑体;最终在中后缘滑体的推挤作用下,主滑区前缘(5号区域)及剪切挤压区(2号区域)完全失稳,并滑入綦江中,形成滑坡坝,滑坡左侧也有部分溜滑体滑至铁路隧道雷吼洞洞口,堵塞铁路线(见图8、图9)。

图8 不同区域的滑动结果

图9 数值模拟计算结果
通过模拟结果中溜滑体和滑坡坝的各点坐标和高程,得到如下结果:溜滑体堵塞铁路面积约为452 m2,平均厚度为1.6 m,体积约为723 m3;滑坡堵塞河道面积约为20 139 m2,宽度为40~102 m,最大高度为14 m,前缘滑块入水速率为20 m/s,最高水位高程达304 m,未超过川黔线铁路运营高程(310 m),不会影响铁路运营。
2.4 危险性分区云图
通过数值模拟和无人机航拍,获得了滑坡范围内的滑块数量、滑动速率、滑坡诱发次生灾害的概率以及植被覆盖情况,并将以上四个指标因素用于危险性分区的定量评价。
首先,设定每个块体对某点人员造成伤亡的概率为0.5,某点滑块砸中人员的概率划分为:小于75%、75%~97%,大于97%三种标准。某点滑块数量基准值为2和5;人一般奔跑速率为5~7 m/s,走路的速率为0.5~1 m/s,将人能够安全逃出的速率(0.5 m/s)设定为打分基准值,从而获得某点各指标因素的分值。而后,通过层次分析法(AHP法)建立判断矩阵[18],归一化后计算得出四个指标因素的权重值(见表2)。最终,通过所得权重值乘以相应各指标因素的分值,得到该点的最终评分值。

表2 单体滑坡危险性分区打分
依据相应的危险性分区,判断该点最终评分值所处区域,绘制准确的危险性分区图,并采取相应的防灾减灾措施(见表3)。

表3 危险性分级及防灾措施
根据以上危险性分区评价准则,将数值模拟计算结果网格化,共建立38个点(见图10)。分别对各点滑块数量、滑动速率、滑坡诱发次生灾害的概率、植被覆盖情况这四个指标因素进行打分,并乘以相应的权重,最终获得各点总分值(见表4)及裁缝岩滑坡准确的危险性分区(见图11)。
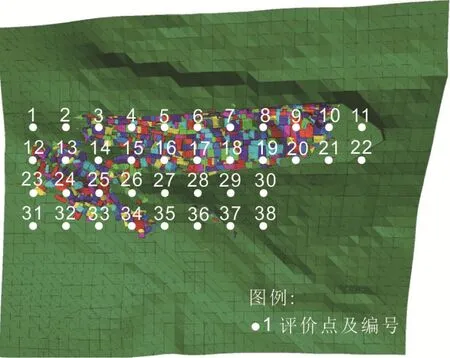
图10 滑坡数值模拟计算结果

图11 裁缝岩滑坡的危险性分区

表4 裁缝岩滑坡危险性评价打分
3 滑坡失稳概率分析
3.1 触发滑坡失稳的降雨量阈值
裁缝岩滑坡发生于2016年6月28日19∶30。滑坡附近有两处雨量监测站,分别为距离滑坡点2.1 km的岔滩站,距离滑坡点5.1 km赶水站。从滑坡失稳前岔滩站和赶水站两处降雨降雨量统计资料(见图12、图13)中可以发现,只有3日累计降雨量的峰值时间点与滑坡失稳时间相同(皆为2016年6月28日)。由此可见,3日累计降雨量峰值与滑坡发生的相关度最高。滑坡失稳时,岔滩站的3日累计降雨量峰值为48.7 mm,赶水站的3日累计降雨量峰值为151.5 mm。由于赶水站、裁缝岩滑坡点、岔滩站正好在一条直线上,可通过内插法计算出滑坡失稳时3日累计降雨量的阈值(为78.7 mm)。

图12 岔滩站降雨量

图13 赶水站降雨量
3.2 滑坡失稳概率
根据重庆市綦江区气象局提供的赶水站附近2009年1月1日至2017年12月31日的日降雨量资料,赶水站3日累计降雨量统计曲线如图14所示,9年间,3日累计降雨量超过阈值的次数共计5次,通过触发因素确定裁缝岩滑坡年发生概率为56%。其失稳概率显然超过了社会可以接受的范围,必须尽快进行治理。

图14 2009年至2017年赶水站三日累计降雨量
4 结论与展望
在现场调查、室内试验、稳定性评价的基础上,利用3DEC三维数值模拟的方法模拟裁缝岩滑坡失稳后的运动路径,证实在最不利工况下,滑坡再次失稳后滑体将滑入綦江中,形成体积约14×104m3的滑坡坝,并且有体积约723 m3的溜滑体将滑至川黔铁路雷吼洞洞口,阻塞铁路;其次,将模拟结果与层次分析法相结合,建立危险性分区标准,制作裁缝岩滑坡危险性分区图;最后,通过多年降雨统计资料确定该滑坡发生失稳的降雨阈值(为78.7 mm),滑坡的年失稳概率为56%,明确了滑坡治理的必要性。
