高速铁路运营期轨道检测自由测站测量模式研究

王 磊

(中铁工程设计咨询集团有限公司，北京 100055)

1 概述

为保证高速铁路的正常运行，必须定期对线路的精密测量控制网与轨道进行复测，保证线路的高可靠性、高稳定性、高平顺性[1]。关于精密控制网与轨道测量方法，诸多学者与工程技术人员已进行了一些研究。杨成宽[2]对施工建设期如何利用GEDO CE轨道检测系统进行轨道精调做了详细介绍；杨昊[3]对运营阶段CPⅢ控制网复测方法及优化方案进行了详细研究；马俊，郑健[4]介绍了CPⅢ平面网复测中约束点的选择方法；王鹏，潘正风[5]提出CPⅢ点位精度是影响轨道调整精度和平顺性的直接因素。从已有研究来看，大多数聚焦于其中一种方法的研究与优化，并未全面考虑精密控制网测量与轨道测量两者的共同点，以下将深入研究两个工序的特点与相互关系，探索一种高效率的测量方法。

高速铁路运营期设备管理单位负责精测网的日常维护工作，当精测网点位因破损、遮挡、形变等原因无法使用，或者距离上一复测周期超过规定年限时，设备管理单位将根据需要提出精测网复测要求。测量单位在完成复测工作后，与上一次的复测成果进行对比分析，判断是否存在形变较大的运营地段。设备管理单位对复测成果进行评审，以确定存在区域沉降、差异沉降或轨道异常变形地段[6]。在运营期，精密测量控制网的主要作用是进行线路设备检测和轨道测量，即利用轨道控制网CPⅢ指导轨检小车进行轨道测量工作[7]，得到轨道绝对位置与设计的偏差值(即线路的横向偏差与高程偏差值)，据此制定线路维修方案。

由前述可知，因线路存在变形，需要实时进行轨道控制网CPⅢ复测工作，而轨道控制网CPⅢ的复测与轨检小车测量都需要对轨道控制网CPⅢ进行测量(即需对同一个地方测量两次)。在高速铁路运营期，上线测量工作都需要在天窗时间进行，而天窗作业时间较短(一般为4 h左右)。因此，如何高效利用轨道控制网CPⅢ指导轨检小车进行轨道测量工作值得研究。

2 轨道控制网CPⅢ复测与轨检小车测量

2.1 轨道控制网CPⅢ复测

轨道控制网CPⅢ复测主要包括平面与高程测量两项工作。

平面复测:首先测量基础平面控制网CPⅠ，然后以CPⅠ网为基础，测量线路平面控制网线上加密CPⅡ点，最后对轨道控制网CPⅢ进行复测。复测应按照与既有精测网“分级复测、同网形、同精度”的原则进行。轨道控制网CPⅢ平面复测采用自由设站边角交会的方法。全站仪的标称精度为0.5″、±(0.6+1×106D)mm，每一测站至少需要进行2个测回的测量。如图1所示，全站仪观测一站内12个CPⅢ点的水平方向、天顶距和斜距，之后通过评审合格的数据处理软件平差得到CPⅢ平面坐标[8]。

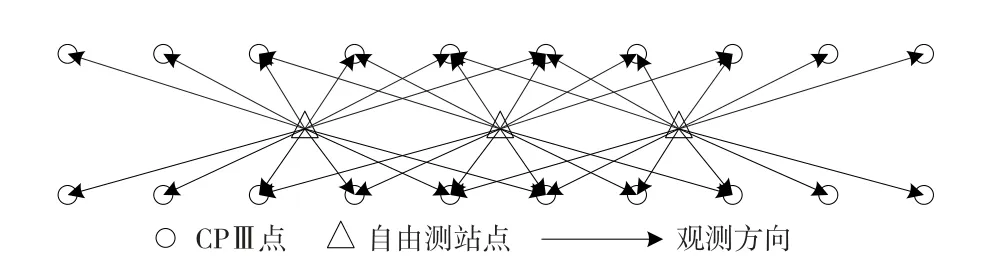
图1 轨道控制网CPⅢ平面复测示意

高程复测:首先复测线路水准基点控制网，再通过线上线下高程联测将水准基点的高程引测至线上。在复测过程中，应按照与既有精测网“同网形、同精度”的原则进行。高程复测可采用水准仪测量方式或全站仪三角高程测量方式进行，当采用全站仪三角高程测量方式进行复测时，需根据文献[7]相关限差要求进行数据采集。水准仪测量方式复测示意如图2。

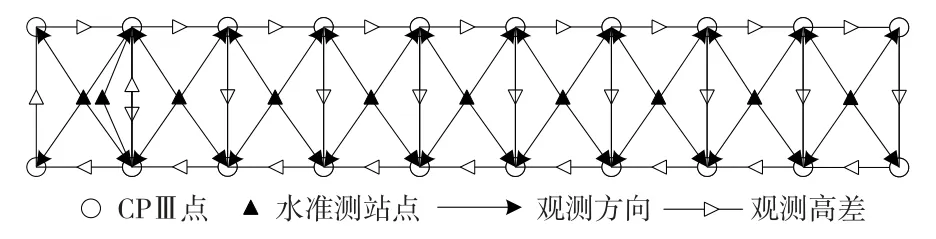
图2 轨道控制网CPⅢ高程水准仪矩形环复测示意

2.2 轨检小车测量

在复测得到轨道控制网CPⅢ的平面坐标和高程后，采用全站仪自由设站方式配合轨检小车进行轨道测量，如图3所示。结合已知的轨道控制网CPⅢ平面坐标和高程，计算全站仪设站处的平面坐标和高程[3]，其中X、Y、Z三个方向的中误差≤0.7 mm，定向角精度≤2″，用于设站的CPⅢ控制点的X、Y、Z不符值≤2.0 mm。再通过极坐标测量方式得到小车上棱镜的平面坐标与高程，结合轨检小车的参数和线路设计参数，计算轨道的横向与高程偏差值[9-10]。

图3 全站仪自由设站配合轨检小车轨道测量示意

高速铁路运营期天窗时间一般为4 h，轨道控制网CPⅢ平面复测一个作业组需要4人，一个天窗的作业效率是1.3～1.6 km；轨道控制网CPⅢ高程复测水准测量一个作业组需要4人，一个天窗的作业效率是1.5～1.8 km；轨检小车一个作业组需要4人，一个天窗的作业效率是0.5～0.6 km。

3 轨道检测自由测站测量模式

3.1 轨道检测自由测站测量模式

为了提高轨道精确检测的作业效率，提出一种同时进行轨道控制网CPⅢ复测与轨检小车测量的新方法，即轨道检测自由测站测量模式。先根据自由测站数据解算CPⅢ控制点坐标，再以CPⅢ控制点坐标为起算数据，采用三维平差的方法解算全站仪站心坐标，进而求得轨检小车上的棱镜坐标，并最终得到轨道检测数据。具体步骤为:

(1)轨检小车进行全站仪自由测站观测时，相邻自由测站点间距离为60 m，轨道控制网CPⅢ数量由8个增加到12个，角度观测由半测回增加为2个测回[6-7]。

(2)按照轨道控制网CPⅢ平面测量与三角高程测量的外业观测限差记录原始数据[3]，包括全站仪自由测站点到CPⅢ点的水平方向、天顶距和斜距；每个CPⅢ点将被四个测站交会测量，提高了网的可靠性，进一步保证了自由测站三角高程计算的精度[11]。

(3)首先进行测回内、测回间的数据限差检查，确保原始数据的观测质量；利用已知的CPⅢ控制点坐标及观测值，采用三维平差的方法得到全站仪站心坐标并设站，直接通过极坐标测量方式观测轨检小车上的棱镜，进行轨道测量。

(4)利用自由测站观测数据，经平差计算得到CPⅢ控制点平面坐标，轨道控制网CPⅢ的高程则通过自由测站三角高程的方法，经平差计算得到[12]。根据检测段的长度选择平差起算点，当长度短于800 m时可以挑选两端稳定的CPⅢ成果作为起算数据[4]，当长度大于800 m时，则选用高等级的控制点成果作为起算数据。

(5)对检测段CPⅢ控制点成果进行更新后，基于最新的CPⅢ复测成果及全站仪自由测站观测值，采用三维平差方法解算站心坐标及定向角，并进行设站精度检查，然后基于重新设站的数据解算轨检小车上的棱镜坐标，并最终归算到轨道。

图4 轨道检测自由测站测量模式示意

轨道检测自由测站测量模式相较于单纯的轨检小车测量，一个作业组需要的人数也为4个，增加测量时间的工序为完成2个测回的轨道控制网CPⅢ观测。根据多站轨道控制网CPⅢ外业观测数据统计，得出全站仪一个自由测站完成2个测回的观测时间为5～6 min，假设一个天窗测量7站，则需多用35～42 min，作业效率减少0.1 km左右，则一个天窗的作业效率为正线长度0.4～0.5 km。

3.2 自由测站三维平差的数学模型

为了提高控制网的高程精度，假设同一测站上各个视线方向都具有相同的折光系数k，把折光系数作为附加未知参数引入天顶距的平差函数模型中，在平差时确定折光系数，并自行消除对天顶距的影响[13-14]。设在自由测站点i观测CPⅢ点为j，对方向Lij、天顶距Aij和斜距Sij分别列立误差方程[15-16]，式(1)、式(2)、式(3)分别为Lij、Aij和Sij观测值对应的线性化后的误差方程[17]

式中，ω为定向角，R为地球曲率半径；k为大气折光系数，X0i、Y0i、Z0i为设站点i的近似坐标，X0j、Y0j、Z0j为点j的近似坐标。D0ij为平距近似值，T0ij为方位角近似值，ω0i为定向角近似值，A0ij为天顶距近似值，S0ij为斜距近似值，有

按全站仪的标称精度确定各个观测值的权值，在很多情况下不够精确。自由测站中多余观测量较多，为了提高定权的精确，推荐使用Helmert方差分量估计定权[18-19]。

根据间接平差原理，可得到误差方程式

按最小二乘原理可得未知数向量

平差后观测值单位权中误差计算公式

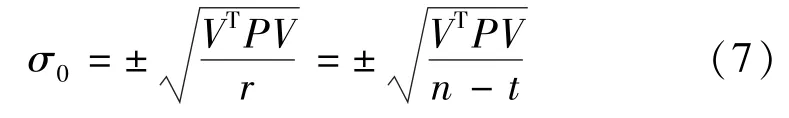
根据协因数传播律，可得未知参数协因数阵为QX=(BTPB)-1，设站点在X，Y，Z坐标轴方向上的坐标中误差、定向角中误差、大气折光参数中误差，可分别按式(8)计算

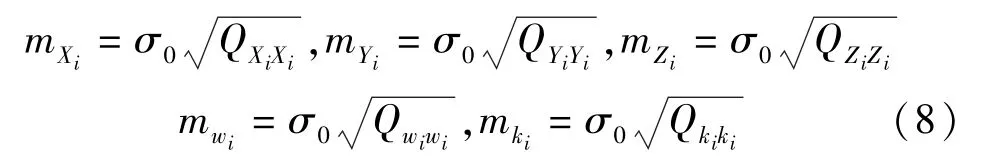
4 实例分析

在某新建高速铁路选取一段长度约500 m的线路进行验证(该段已提前完成线下平面与高程起算点的复测)，首先对轨道控制网CPⅢ进行复测，得到最新的CPⅢ平面坐标和高程，之后立即利用自由设站模式进行轨检小车测量，上述两个步骤可在2 d内完成，故将本次测量(自由设站模式)得到的线路横向偏差和高程偏差作为真值。

采用轨道检测自由测站测量模式观测线路数据，通过三维平差计算得到自由测站点的平面坐标和高程，再处理得到对应的线路横向偏差和高程偏差。最终对比该线路上行线自由设站与自由测站模式的横向偏差与高程偏差(如图5、图6所示)。

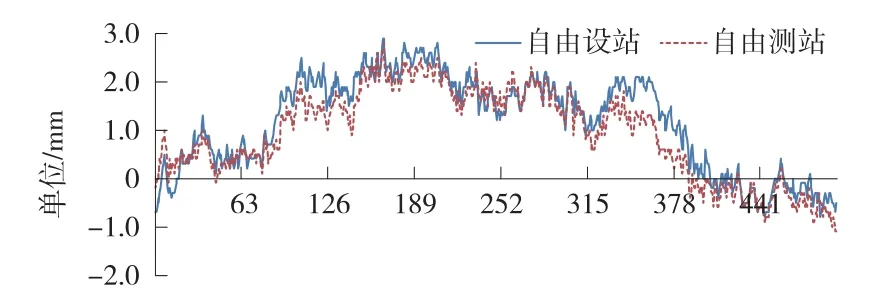
图5 自由设站与自由测站横向偏差比较

图6 自由设站与自由测站高程偏差比较

由图5与图6可知，自由设站与自由测站模式下线路的横向偏差与高程偏差吻合较好。为进一步分析偏差的精度，将自由设站与自由测站模式下线路的横向偏差与高程偏差分别作差，如图7、图8所示。

图7 自由设站与自由测站横向偏差之差

图8 自由设站与自由测站高程偏差之差

由图7可知，该实验段自由设站与自由测站横向偏差之差最大值为0.9 mm，最小值为-0.7 mm，均值为0.2 mm，其中100%在±1 mm以内。由图8可知，该实验段自由设站与自由测站高程偏差之差最大值为0.5 mm，最小值为-0.9 mm，均值为-0.4 mm，其中100%在±1 mm以内。综上所述，轨道检测自由测站测量模式与分步测量模式得到的线路横向偏差和高程偏差的差值都在±1 mm以内，满足轨道检测的精度要求。

5 结论

当检测段长度为1 km时，轨道控制网CPⅢ复测与轨检小车分步测量需要4个天窗，轨道检测自由测站测量模式只需要2～3个天窗；当检测段长度为5 km时，轨道控制网CPⅢ复测与轨检小车分步测量需要14个天窗，轨道检测自由测站测量模式只需要10个天窗。综上所述，轨道检测自由测站测量模式减少了上线时间，提高了轨道检测的作业效率。通过实例分析验证，轨道检测自由测站测量模式与分步测量模式得到的线路横向偏差和高程偏差的差值都在±1 mm以内，满足轨道检测的精度要求，三维平差计算所使用的数学模型正确，精度可靠，测量效率提高30%以上。