基于Android平台并行运算机制的密码运算加速方案1

方宁，曹卫兵，倪冬鹤，狄冠东,3

（1. 北京梆梆安全科技有限公司，北京 100091；2. 北京电子技术应用研究所，北京100091；3. 青岛大学计算机科学技术学院，山东 青岛 266071）

1 引言

近年来，移动智能设备的普及和移动互联网的快速发展为人们的工作和生活带来了极大便利，与此同时，越来越多的个人信息甚至个人隐私不可避免地在网络交互过程中被传输、处理、存储。由于计算机网络的开放性、复杂性和多样性，移动终端面临的安全风险种类繁多而且不断更新。

密码技术是信息安全的核心和关键技术，能够为保护网络空间信息安全提供有效的机制。其中，非对称密码技术主要应用于身份认证、完整性保护和数字签名等场景，在移动终端中的使用非常普遍，因为它涉及了移动互联网应用中绝大多数安全需求的解决方案。与对称密码体制相比，非对称密码体制具有密钥管理高效等诸多优势，但是速度相对较慢，当应用于数据加密场景时，适合于数据量较小的加密操作。而在移动互联网应用场景中，密码运算的执行速度直接决定了终端用户的使用体验。如何在保证安全性的同时，进一步提高密码运算的执行效率和执行速度，缩短用户操作相应时间，一直以来都是移动应用设计与开发人员研究的热点问题[1]。在不同的软硬件体系结构中，可以采用特殊的设计方法，利用体系结构特点实现多种运算的加速操作。本文方案利用Android平台中的并行运算机制，研究椭圆曲线密码基本运算的加速和优化方法。

椭圆曲线密码是一类常见的非对称密码技术，具有密钥长度较小、运算速度快等优势，被广泛应用在嵌入式设备、移动终端和其他应用场景中[2]。椭圆曲线密码通常基于有限域中元素构建，其基本运算包括有限域中元素的加法、乘法、求逆等。而这些运算需要以大整数的加法、乘法、模运算作为基础运算。一次椭圆曲线上典型运算的实现，需要调用多至几十次的大整数运算[3]。因此，提高大整数运算的执行速度，对于提高椭圆曲线密码的执行效率具有非常重要的意义。此外，大整数运算还具有很多数值计算的应用，对于以大整数运算作为基础的应用，寻找快速有效的大整数计算方法也非常必要[4]。

大整数通常指的是数值超过了程序设计语言中一般整数类型变量表示范围的整数，位数一般在几百或几千位。对于此类数值的运算，需要另外设计其表示方法和计算方法。Java[5]和微软.NET[6]框架中都有相应的大整数类，用以完成上述任务。大整数的各种运算中，加法和减法相对简单，乘法最为困难，模运算可以转化为乘法实现[7]。因此，本文针对大整数的乘法运算这一主要问题，利用Android平台的并行运算机制，设计了一种高效快速的计算实现方法。

目前的大整数乘法计算方法中，大部分是基于串行算法的。在 Android平台上采用这些方法时，利用的是CPU的计算资源。现有的大整数乘法并行计算技术主要利用的是 CUDA（compute unified device architecture）框架[8]。该框架是NVIDIA推出的运算平台，使设备中的图形处理器（GPU，graphics processing unit）能够解决复杂的计算问题。Android系统不支持CUDA框架，因此无法使用现有技术。本文使用的是Android平台的RenderScript编程框架[9]。RenderScript是一套Android平台上运行3D渲染和处理密集型计算任务的编程框架，主要面向的是具有并行数据处理特点的计算任务，可以将计算任务并行化，将其分配给移动设备上所有可用的处理器单元，如多核的CPU、GPU等。RenderScript编程框架具有极高的设备无关性和可移植性，能够在运行Android平台的任何移动设备中部署使用。Android系统从3.0版本开始集成了RenderScript，从4.3版本开始将其作为系统中唯一的并行计算编程框架。

2 大整数乘法并行计算方案

GPU的优势在于GPU的众核架构支持大量的并发线程同时执行不同输入的相同指令，因此并行算法的设计思路是：将复杂的大数乘法问题分割成若干子问题，分配给GPU不同的核心并行处理，最后整合所有核心的计算结果得到最终结果。并行计算方案设计的关键问题是子任务的划分。划分方法既要分解串行计算过程中最耗时的主要计算任务，同时还要保证所有子任务能够独立、互不影响地被执行。本文将大数乘法算法分为对应相乘、斜向相加、进位整合3个步骤，其中包含两次子任务划分。

2.1 存储结构

首先需要设计能够支持并行计算子任务划分的存储结构。为了完成并行处理的运算，本文采用线性存储结构来存储乘法运算的因子、中间结果和最终计算结果。与传统方案类似，仍然使用整数数组存储大整数[10]。对于参与运算的两个操作数A和B，使用数组A[]和B[]按照从高位到低位的顺序分别对其进行存储，用lenA和lenB分别表示数组长度。构造二维数组map[lenA＋1][lenB＋1]存放对应乘法运算的中间结果，其中下标为0的行和列元素作为预留元素以便处理可能出现的进位。使用数组ans[]保存最终的乘法运算结果，其长度计为lenAns。

2.2 对应相乘

按照上述存储结构设计，使用式(1)即可完成乘法运算。

将二维数组视为矩阵对象，其中元素的值与操作数的对应关系如图1所示。

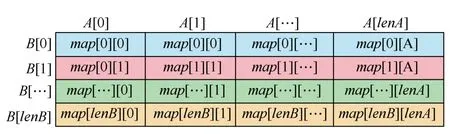
图1 按单元相乘结果矩阵

在串行计算中，要计算得到上述矩阵结果需要进行lenA×lenB次计算，而在并行计算机制中的计算次数为

2.3 斜向相加

在map数组的基础上，需要进行一系列加法运算得到最终的乘法结果。ans数组中各个元素的计算公式如式(2)所示。

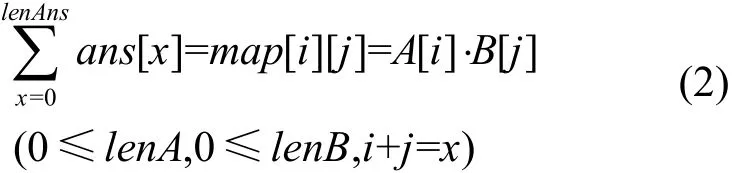
该过程可以被形象地认为是将map数组对应的矩阵对象倾斜 45°后累加垂直方向上的所有元素。如果未发生进位，需要进行累加操作的数组单元数量，即ans数组的长度为lenAns＝lenA+lenB－1；如果出现进位，则该长度为lenA+lenB。

图2为lenA和lenB分别为3时的斜向相加过程。

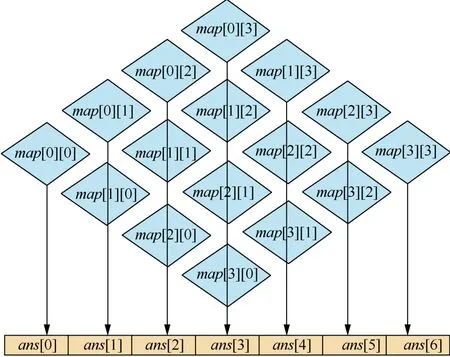
图2 斜向相加过程

2.4 取模进位

经过上述过程得到ans数组元素并未进行进位操作，最终需要的是一个经过进位整理的ans数组，以便继续用于计算或者转换输出。因此，需要从ans数组的最高单元（计算结果的最低单元）开始，进行循环取模和进位操作。循环取模进位结束后，就得到了最终计算结果的数组。

2.5 对并行计算次数的进一步优化

在 RenderScript框架中，每次调用并行计算机制时，都要从内存向GPU缓存传递数据，该过程会造成一定的时间开销。分析上述方案的计算过程发现，虽然在逻辑上可以划分为对应相乘和斜向相加两个阶段，但实际上可以将其合并为一次并行计算机制的调用，从而降低系统时间开销，进一步优化计算过程的执行效率。

具体方法为取消map数组的存储单元，将map数组中所有元素的计算过程合并到原来的并行斜向相加的过程中。即在完成矩阵元素map[i][j]的计算后，即刻将其累加到ans数组的对应元素中。

上述优化方法大大缩减了对存储空间的依赖，将并行计算机制的调用次数减少为原来的50%。

3 实验

在Android平台中使用RenderScript框架实现本文方案分为两步。第一步是创建计算核心文件，该文件中包含编译指示声明、对应的Java类说明和主体计算函数定义。主体计算函数是将计算任务并行化的重要手段，被上层的Java类调用。第二步是创建使用该计算核心的Java类，这里需要声明一个 RenderScript变量，对其分配资源并初始化后用其调用主体计算函数。

本文采用常见的Android Studio作为开发工具[11]，编码实现上文中的方案。通过设置编译配置文件“build.gradle”，在“config”中增加“renderscriptTargetApi”和“renderscriptSupport ModeEnabled”两个字段，使Android Studio支持RenderScript框架的使用。

首先进行核心层的实现。本文将核心文件代码包含在核心文件 mul.rs中，在该文件代码中定义了一个宏、6个全局变量、一个全局静态变量和两个运算接口。定义了一个静态的长整形数组，用于临时保存结果的斜向相加后的计算结果。并行乘法接口将串行算法中的for循环遍历求解数组的过程变为并行调用求解每一个结果数组元素的过程。计算结果存到了临时长整形数组中，以保证数据不溢出，并起到了拓宽取值范围的作用。编写完核心文件后，编译生成对应Java类，用于提供上层Java类与核心进行交互的媒介。

RenderScript核心层实现完毕后，在Java层封装一个RSBigInteger类与核心交互，并提供规范的上层API[12]；进而定义RSBigInteger类的乘法接口，其方法实现中定义了 forEach_multiply方法，实现对核心文件mul.rs中的multiply方法对并行执行调用。

最终，本文将编译完成的运算库进行发布，并编写了测试程序使用RSBigInteger类调用运算库，测试其实际计算性能。本文采用红米2标准版手机作为测试硬件，其系统版本为5.1.1，CPU为高通 MSM8916四核处理器，GPU为高通Adreno306。在同样的设备上，本文编写了使用原生的JavaBigInteger类的另一个测试程序，执行完全相同的计算任务，对计算结果进行比较。实验步骤如下。

1) 生成长度为N的两个随机大整数。

2) 分别使用两个测试程序初始化两个大整数实例，记录初始化耗时。

3) 分别使用两个测试程序做 50次乘法计算，记录执行时间和计算结果。

表1 测试结果

4) 确认计算结果正确的条件下，针对每个长度N的大整数进行3组测试，记录初始化时间和计算时间的平均值。

5) 改变N的值，重复上述过程。

（注：测试中N的取值为100，300，500，800，1 000，3 000，5 000）。

实验结果如表1所示。

使用JavaBigInteger类和RSBigInteger类的测试程序在初始化操作方面的时间比较如图 3所示，其计算时间比较如图4所示。

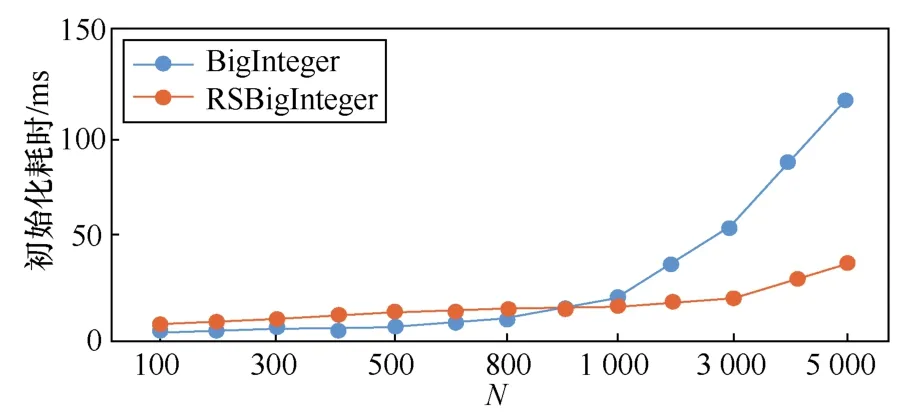
图3 初始化时间表比较

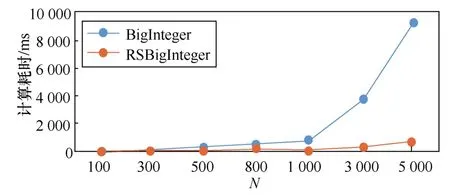
图4 计算时间比较

从图3中可以明显看出，大整数长度低于900 bit时使用RSBigInteger类的测试程序初始化速度不占优势。这是因为初始化函数中要提前构造用于GPU并行计算使用的存储对象。但是使用BigInteger类的测试程序初始化时间是呈线性增长的，而使用RSBigInteger类的测试程序的增速非常缓慢。

从图4中可以看出，随着计算量的增大，传统基于CPU的串行算法的BigInteger类耗时呈指数型增长，而使用并行计算算法的 RSBigInteger类耗时增速却非常缓慢。因此在数据量足够大时，GPU并行计算的优势非常明显。

测试结果表明，小规模数据的计算并不适合使用并行计算机制，因为输入输出时间占比过高将导致并行计算的优势无法发挥。对于超过300 bit的大整数而言，使用并行计算机制是非常合适的，而且长度越大，其效果越明显。

4 结束语

本文研究了利用 Android平台中的RenderScript并行运算机制实现大整数乘法快速运算的方法，设计并实现了一种适合并行处理的大整数乘法运算存储结构和运算执行逻辑。该方案以矩阵的方式分割并处理大整数对象，可以并行地同步完成所有乘法和加法运算，进而快速得到乘法运算结果。本文方案能够为椭圆曲线密码等密码运算提供高效快速的基本操作，实现Android平台密码运算的加速与优化。实验结果表明，与Android平台中原生的Java大整数运算库相比，本文方案在执行速度上具有明显优势。