RSA-CRT密码防御算法的故障注入攻击1

孔凡玉，乔咏，刘蓬涛，刘晓东，周大水

（1. 山东大学网络信息安全研究所，山东 济南 250100；2. 中标软件有限公司，北京 100190；3. 山东政法学院网络空间安全学院，山东 济南 250014）

1 引言

自Diffie和Hellman提出第一个公钥密码体制——Diffie-Hellman密钥协商协议[1]以来，公钥密码体制在数字签名、密钥协商等方面发挥了越来越重要的作用。RSA密码算法[2]是最早提出的几个公钥密码体制之一，其安全性基于大整数分解困难问题，可用于公钥加密和数字签名等功能，是几十年以来应用最广泛的公钥密码体制之一。近年来，基于椭圆曲线的SM2密码算法标准和美国的ECDSA数字签名标准逐渐推广，但在IPSec协议、TLS/SSL协议以及浏览器等互联网环境中，RSA密码体制的实际应用依然很广泛，其安全性分析非常重要。

长期以来，密码攻击者主要从数学计算的角度分析一个密码算法的安全性，如通过大整数分解等方法攻击RSA密码体制。但是，Kocher等学者提出的侧信道攻击[3-5]拓展了传统密码分析的思路，能够利用密码算法实际执行时泄露的运算时间、电量消耗等信息恢复部分甚至整个秘密密钥。被动式的侧信道攻击通过测量密码运算的执行时间、电量消耗等信息分析密钥，不影响密码运算的正常执行；主动式的侧信道攻击则可以改变密码运算的执行过程，使其产生对密码分析有用的信息，故障注入攻击是一种主动式攻击方法。

Dan Boneh首次提出了故障注入攻击[4]的概念，并提出了针对RSA密码的中国剩余定理实现（RSA-CRT）的攻击方法：当其中一个模幂运算发生错误时，可以通过错误的RSA签名结果恢复 RSA私钥。Shamir[6]通过在 RSA运算过程中引入一个随机数r来判断两次模幂的结果是否存在错误，如果检测到错误，则只返回错误提示，不返回错误的RSA签名值，因此避免攻击者使用错误的签名值恢复私钥。Joye等学者[7]进一步改进、细化了Shamir的方法，使用dp和dq替代私钥指数d。Aumüller等[8]指出，在Shamir的方法中，如果计算两次模幂的过程中不出错，而是在中国剩余定理的结果合成运算中注入错误，使其中一个模幂结果出错，则仍然能够成功攻击。Yen等[9]详细分析了Shamir的方法和Aumüller的改进方法，对RSA-CRT的故障注入攻击方法进行了系统的论述。

在FDTC 2014会议上，Rauzy和Guilley[10]对基于检测和基于感染计算的两类故障注入防御算法进行了分析，并提出了多个抵抗故障注入攻击的算法。2016年，Battistello和Giraud[11]对Rauzy和 Guilley提出的感染计算的防御算法进行了分析，证明其不能抵抗故障注入攻击。关于RSA-CRT密码算法的故障注入攻击和防御措施，可以参见相关参考文献[12-22]。

本文针对Rauzy和Guilley提出的两个基于检测的 RSA-CRT安全防御算法，进行故障注入攻击，在 RSA密码运算过程中注入一个永久性错误，使防御算法不能检测到错误的发生，然后利用错误的RSA签名运算结果，计算出RSA私钥。此攻击表明，Rauzy和Guilley的RSA安全实现算法不能抵抗故障注入攻击。

2 RSA-CRT密码算法和故障注入攻击

本节介绍 RSA密码算法的中国剩余定理实现，以及针对 RSA-CRT实现的故障注入攻击和防御措施。

2.1 RSA密码和中国剩余定理实现

RSA密码算法[2]是基于整数分解困难问题的公钥密码体制，其公钥包括模数N和公钥指数e，其中N=pq，为了保证安全性，要求p和q为512 bit以上长度的素数。RSA密码的私钥为p、q和私钥指数d，满足e·d≡1 modφ(N)，其中，φ(N)=(p–1)·(q–1)是欧拉函数。

RSA加密或验证签名的过程，即计算模幂MemodN；RSA解密或签名的过程，即计算模幂MdmodN。为了提高加密和验签的速度，一般选择比较短的公钥指数e，如e=65 537，私钥指数d是与模N长度相同或接近的整数，RSA私钥运算S=MdmodN的时间复杂性为O(log3(N))。

采用中国剩余定理可以提高 RSA私钥运算的速度（简称 RSA-CRT），即先计算两个模幂Sp=Mdpmodp和Sq=Mdqmodq，然后组合成最后的计算结果。

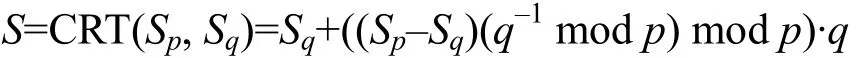
其中，dp=dmod (p–1)，dq=dmod (q–1)。由于素数p和q的长度为模N的一半，因此每次Sp或Sq的计算量约为计算S=MdmodN的所以采用中国剩余定理能够提高约4倍速度。

2.2 RSA-CRT密码的故障注入攻击

当RSA-CRT运算中的一个模幂运算Sp=Mdpmodp发生错误，即得到错误的模幂结果S′p，那么最后的RSA-CRT运算结果为

根据RSA-CRT的正确运算结果S和错误结果S′，可以通过欧几里得算法计算出素数q，即计算[4]

或者由 RSA-CRT的错误结果S′，直接计算出素数q，即计算

存在两大类抵抗故障注入攻击的RSA-CRT实现算法：一类是 Shamir[6]提出的基于错误检测的方法，随机选择一个随机数r，用于盲化素数p和q，先计算模pr和qr的模幂，然后通过模r运算判断两次模幂的结果是否存在错误，如果判断没有错误，则正常计算并返回结果RSA签名S，否则，返回计算失败；另一类是基于感染计算的方法[12]，即不管是否存在模幂运算错误，都返回RSA签名结果，但利用错误的RSA签名结果不能计算出秘密素数p或q。文献[10,17]对 RSA-CRT密码的故障注入攻击和防御方法进行了详细论述。

3 Rauzy等提出的RSA-CRT密码防御算法

Rauzy和Guilley在FDTC 2014会议上的论文[10]系统地分析了基于检测和基于感染计算的两类故障注入防御算法，指出这两类算法之间可以通过一定的方法相互转化。Rauzy和Guilley[10]认为，基于感染计算的抵御算法比基于检测的算法更好，因为它避免了分支判断，减少了故障注入的可能性，同时提出了多个抵抗故障注入攻击的算法。但 Battistello和Giraud[11]对Rauzy和Guilley提出的两个感染计算的防御算法进行了分析，表明其不能抵抗故障注入攻击。

本文主要对Rauzy和Guilley提出的基于检测的防御算法[10]进行分析，一个被称为“一种直接的防御算法”（原文中的Algorithm 9），另一个是改进的Shamir方法（原文中的Algorithm 10）。下面分别对这两个算法进行简要描述。

3.1 一种直接的RSA-CRT防御算法

Rauzy和Guilley提出的“一种直接的防御算法”（参考文献[10]中的Algorithm 9）是对模幂Sp、Sq和 CRT绑定结果均进行验证，并被证明能够抵抗一阶故障注入攻击，其算法描述如下。

算法1一种直接的RSA-CRT防御算法[10]

输入：消息M，密钥（p,q,dp,dq,iq）

输出：RSA签名值MdmodN，或返回失败

Begin

Step 1Sp=Mdpmodφ(p)modp；

Step 2ifSp≠Mdpmodpthen return error；

Step 3Sq=Mdqmodφ(q)modq；

Step 4ifSq≠Mdqmodqthen return error；

Step 5S=CRT(Sp,Sq)=Sq+q·(iq·(Sp–Sq) modp)；

Step 6if ((S≠Spmodp) or (S≠Sqmodq))then return error；

Step 7returnS；

End

3.2 改进的Shamir防御算法

Rauzy和Guilley提出的改进的Shamir方法（参考文献[10]中的 Algorithm 10）对原来的Shamir方法进行了修改，并被认为能够抵抗故障注入攻击，其算法描述如下。

算法2RSA-CRT实现的改进Shamir防御算法[10]

输入：消息M，密钥（p,q,dp,dq,iq）

输出：RSA签名值MdmodN，或返回失败

Begin

Step 1选择一个小的随机数r；

Step 2p′=p·r；

Step 3q′=q·r；

Step 4if ((p′≠0 modp) or (q′≠0 modq))then return error；

Step 5S′p=Mdmodφ(p′)modp′；

Step 6S′q=Mdmodφ(q′)modq′；

Step 7ifS′p≠S′qmodrthen return error；

Step 8Sp=S′pmodp；

Step 9Sq=S′qmodq；

Step 10S= CRT(Sp,Sq) =Sq+q· (iq· (Sp–Sq)modp)；

Step 11if ((S≠S′pmodp) or (S≠S′qmodq))then return error；

Step 12returnS；

End

4 针对Rauzy等的RSA-CRT防御算法的攻击

Yen等[9]将故障注入攻击中发生的错误分为两类：一类是暂时性的错误，即仅在这一次运算时某个数据临时出错，之后恢复原来的正确值；另一类是永久性的错误，即在某个时间点修改了某个数据后，这个错误值将一直保持到整个RSA运算过程结束。对RSA-CRT密码算法的故障注入攻击方法，包括在 RSA运算过程中的哪个时间点注入错误，以及注入的是临时性错误还是永久性错误。根据注入错误的次数，可以分为一阶故障注入攻击、二阶故障注入攻击等，分别表示攻击者能够在RSA运算过程中注入一个、两个以及更多的错误。

本文主要对Rauzy和Guilley提出的基于检测的防御算法的故障注入攻击，采用了一阶故障注入攻击方法，产生的是一个永久性错误，并能够顺利通过防御算法的错误检测流程，从而导致产生、输出一个错误的RSA签名结果，以用于求解 RSA私钥。下面分别对这两个算法的攻击方法进行描述。

4.1 对算法1的故障注入攻击

Rauzy和Guilley提出的“一种直接的防御算法”（算法1），分别在Step 2和Step 4对模幂Sp、Sq结果进行错误检测，在Step 5进行CRT组合运算，然后在Step 6检测CRT组合运算结果是否有错误。

本文提出的故障注入攻击方法是在Step 5计算过程中，对Sp注入一个永久性错误，攻击方法描述如下。

攻击方法1针对算法1的故障注入攻击

输入：消息M，密钥（p,q,dp,dq,iq）

输出：RSA签名值MdmodN，或返回失败

Begin

Step 1Sp=Mdpmodφ(p)modp；

Step 2ifSp≠Mdpmodpthen return error；

Step 3Sq=Mdqmodφ(q)modq；

Step 4ifSq≠Mdqmodqthen return error；

Step 5对Sp注入一个永久性错误，即将其修改为S′p，计算：

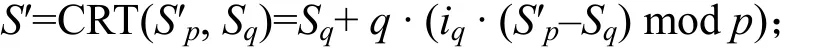
Step 6if ((S′≠S′pmodp) or (S′≠Sqmodq))then return error；

Step 7returnS′；

End

下面说明故障注入攻击方法1能够成功恢复RSA私钥。

首先，本文的攻击方法不改变 Step1～Step4的运算，因此Step1～Step4能够顺利执行，不会返回错误。然后，在Step 5中，对Sp注入一个永久性错误，即将其修改为S′p，并计算S′=CRT(S′p,Sq)。因为S′p是一个永久性错误，CRT组合运算只是按照上面的运算公式计算S′，其结果S′依然满足S′=S′pmodp和S′=Sqmodq，因此 Step 6 并不能检测到S′p的错误，Step 7会返回一个错误的RSA签名值S′。根据错误的RSA签名值S′，容易计算出素数q=GCD((S′e–M) modN,N)，从而恢复 RSA私钥。

4.2 对算法2的故障注入攻击

Rauzy和Guilley提出的改进的Shamir方法（算法2），在Step 4检测p′和q′的正确性，在Step 7 检测模幂S′p、S′q的正确性，在 Step 10 进行 CRT组合运算，然后在Step 11检测CRT组合运算结果是否存在错误。

本文提出的故障注入攻击方法是在Step 8计算过程中，对S′p注入一个永久性错误，攻击方法描述如下。

攻击方法2针对算法2的故障注入攻击

输入：消息M，密钥（p,q,dp,dq,iq）

输出：RSA签名值MdmodN，或返回失败

Begin

Step 1选择一个小的随机数r；

Step 2p′=p·r；

Step 3q′=q·r；

Step 4if ((p′≠0 modp) or (q′≠0 modq)) then return error；

Step 5S′p=Mdmodφ(p′)modp′；

Step 6S′q=Mdmodφ(q′)modq′；

Step 7ifS′p≠S′qmodrthen return error；

Step 8对S′p注入一个永久性错误，即将其修改为S′*p，计算：S*p=S′*pmodp；

Step 9Sq=S′qmodq；

Step 10S*=CRT(S*p,Sq)=Sq+q· (iq· (S*p–Sq)modp)；

Step 11if ((S*≠S′*pmodp) or (S*≠S′qmodq))then return error；

Step 12returnS*；

End

下面说明故障注入攻击方法2能够成功恢复RSA私钥。

首先，本文的攻击方法不改变 Step1～Step7的运算过程，因此不会返回错误。然后，在Step 8中，对S′p注入一个永久性错误，即将其修改为S′*p，并计算出一个错误的模幂值S*p=S′*pmodp。在Step 10中，CRT组合运算将错误的模幂S*p和正确的模幂Sq进行组合计算，得到错误的S*。因为在Step 8中，S*p是由S′*p模p计算出来的，因此 Step 11 中的S*满足S*=S′*pmodp和S*=S′qmodq。所以，Step 12会返回一个错误的RSA签名值S*。根据错误的RSA签名值S*，容易计算出素数q=GCD((S*e–M) modN,N)，从而恢复RSA私钥。

不管在硬件还是软件实现中，Sp和S′p等大整数都是以数组的形式存储在内存或寄存器中，如在Intel CPU中，可以是以32或64比特为单位的数组进行存储。所以，本文提出的故障注入攻击，只要对Sp和S′p等数据的某一个32或64比特存储单位进行修改，就可以实现相应的故障注入攻击。

5 结束语

故障注入攻击等侧信道攻击方法表明，一个密码算法的正确、安全实现与其安全性密切相关。针对 RSA-CRT密码实现的故障注入攻击是一种很强大的攻击技术，仅需要一次模幂出现错误即可攻击成功，因此必须采用安全的实现算法以抵抗故障注入攻击。

本文对Rauzy和Guilley提出的两个故障注入攻击算法进行了分析，提出了一阶故障注入攻击算法，表明这两个算法不能抵抗故障注入攻击。如何在抵抗故障注入攻击的同时，提高RSA-CRT密码实现的速度，并分析在手机、物联网、车联网等移动环境下的实际攻击技术，是下一步需要研究的方向。