股票市场风险测度方法：文献综述

黄冬阳，宋光辉（博士生导师），董永琦

一、引言

自现代金融体系建立以来，风险与收益相匹配的原则得到了理论界和实务界的广泛认可。因此，在金融实务中如何对风险进行有效的测度和衡量成为金融研究工作者重点关注的话题。股票市场因其参与个体众多，风险的时变性和跳跃性更为明显，因此，对股票市场风险的有效测度成为学术界需要重点突破的一个领域。

本文对半个世纪以来关于股票市场风险测度的主要方法和实证文献进行了综述。首先，根据设置的文献检索组合框检索得到相关文献；然后，将现有的股票市场风险测算方法分为相对测算法和绝对测算法，并重点分析了当前使用较为广泛的六种股票市场风险测度方法，包括各种风险测度模型的诞生、改良、意义、不足以及在理论和实务领域的应用；最后，对比分析了每个模型的优点、缺点以及适用的情境。本文的研究不仅能使学者们更快、更系统地了解这一领域的研究现状，也能为这一领域未来的突破提供有益的思路。

二、文献检索方法

本研究采用的是循证文献检索法，该方法是从研究现象出发探求其背后的支撑理论，研究重点是股票市场风险度量方法的相关研究文献。因此，以“股票市场风险度量”为主框架生成搜索条件。由于股票市场风险度量（Stock Market Risk Measurement）有不同的表述方式，如股价波动率测度（Stock Price Volatility Measurement）、金融市场风险测度（Financial Market Risk Measurement）、股票收益率波动性测度（Volatility Measure of Stock）、金融市场不确定性及风险度量（Financial Market Uncer-tainty and Risk Measurement）等。将这些词汇作为主框，在中国知网、Web of Sciences、EBSCO、Wiley、Springer等中外数据库中按标题、摘要及关键词进行搜索。

为了缩小研究范围，设定不同子框内容。因为本文最终探讨的是风险，所以先从风险出发，将“市场风险”（Market Risk）、“不确定性”（Uncertainty）作为第一个子框中识别论文的关键词。由于股票市场的风险反映在股票价格以及收益率的波动上，因此将“价格波动”（Price Fluctuations）、“收益率波动”（Rate of Return Fluctuation）归入第二个子框。从时间维度上看，本研究更关注短期的股价异常波动，故将“短期”（Short Term）、“异常波动”（Abnormal Fluctuations）归入第三个子框。在文献检索过程中，由每个子帧所产生的新术语与前一个子帧的术语相结合，以确保检索所有可能的组合。在对第三个子框进行手工筛选后，没有发现任何用于衡量股票市场风险的新术语，表明检索结果是全面的，并最终形成文献检索组合框，如图所示：

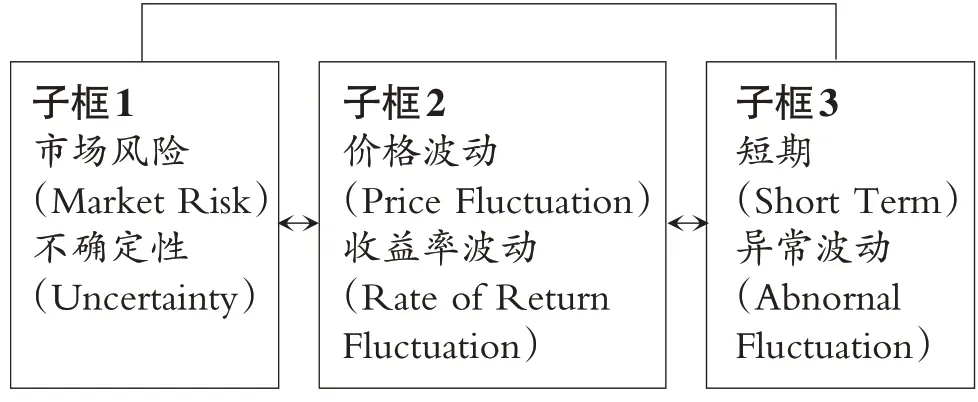
文献检索组合框

按照上述方法，检索得到95 篇初始文献，首先筛选掉与研究主题无关的文章，然后以CSSCI 中文社会科学引文索引（2017～2018）和SSCI、SCI 等国外权威索引收录为期刊文献择取范围，得到用于定性分析股票市场风险测度模型的文献74篇，其中外文文献42篇，国内文献32篇。

三、股票市场风险测算方法分类

魏宇等[1]指出，在股票市场风险管理领域，从股价波动率是外在影响因子还是内在波动幅度的分析标准出发，可以将市场风险测度方法划分为相对测算法和绝对测算法两种。其中，相对测算法主要是测量各种市场因子（包括利率、汇率等）的波动对股票价格波动率的影响程度，绝对测算法计算的主要是股票价格或者收益率波动的幅度。具体模型方法如表1所示。

表1 股票市场风险测算方法

四、股票市场风险度量模型的具体介绍

（一）风险价值法（VaR）

1994年J.P.Morgan[6]（摩根银行）开发出了以严谨、系统的概率统计理论作为依托的用于测量市场风险的“风险度量制”模型，并将VaR 定义为：在仓位被注销或重估之前可能发生的市场价值的估计最大值。1997年P.Jorion 发表的论文《In Defense of VaR》中对VaR 的定义是：VaR 表示某一目标期间可能发生的最大损失，即：Prob（△p＞VaR）=1-α（α表示置信水平）。

根据不同市场因素预测方法的分类，VaR 法的参数估计先后经历了历史模拟法、方差—协方差方法以及蒙特卡罗模拟法。历史模拟法只关注市场因素波动的历史数据，通过大量的历史数据模拟未来的风险价值，但这种方法由于假设错误，并不符合未成熟的股票市场。方差—协方差方法是一种参数方法，通过确定置信度和分布函数得到VaR 值，但它只是线性地将风险因子和金融资产联系起来。蒙特卡罗模拟法通过随机概率的方法输出结果，同时会记录这个过程中发生的各种情景状况。风险价值法（VaR）的演进脉络如表2所示。

20 世纪90年代欧美等发达国家的金融公司纷纷建立风险价值模型以测量金融机构潜在的交易风险损失。1993年，国际清算银行在《巴塞尔协议》中承认了风险价值的VaR模型。1994年摩根银行免费发放VaR 模型计算的信息系统Risk-Metrics 手册，建立了统一的测算标准。至此，VaR 模型前进了一大步。1996年1月，G10签订了《巴塞尔协议》的补充协议，将VaR正式列为确定风险资本充足性的基础方法，促使VaR模型在金融市场风险计量领域占有重要地位。

表2 风险价值法（VaR）演进脉络

国内对VaR 的研究开始于20 世纪90年代，前期重点集中在VaR理论及参数估计上。如：刘宇飞[13]探讨了VaR 方法的含义和应用。21 世纪初，随着VaR 模型在应用中的缺点逐渐显现出来，学者们开始思考对VaR 的前提假定做出修正或者进行模型改进。如：田新时、刘汉中和李耀[14]指出相比正态分布，在GED分布下应用VaR模型估算出的收益率序列能更好地反映肥尾特征，而且需要估计的参数也更少。叶五一、缪柏其和吴振翔[15]针对VaR 模型不能拟合实际收益率序列肥尾特征的弱点，提出参数和非参数估计方法，然后通过实证研究发现修正分布能弥补这一弱点，并且非参数修正得到的VaR拟合程度更好。

风险价值法拒绝假设风险和收益是线性的，并且真实地反映了随机过程。该方法比较简单，用一个指标综合反映金融市场的不同风险，可以用于对股票市场资产组合的整体性风险的前瞻性分析。但其存在着以下四个不足：

1.VaR 模型不能有效刻画现实中金融资产市场价格波动表现出的“尖峰肥尾”的分布特点。陈学华、杨辉耀[16]指出传统VaR模型对尾部风险的研究不够深入，其通过实证研究得出条件极值模型由于基于尾部分布测算而更适合对较小样本的预测的结论。魏宇[17]认为VaR 的正态分布性限制了其应用，其提出了有偏学生分布，并且探讨了在不同收益分布假定条件下的风险价值测算。王灵芝、杨朝军[18]从弥补VaR弱点的角度出发，采用时变条件方差法计算股价的流动性风险，研究结果表明，时变条件方差法更能准确地描绘价格波动率“尖峰肥尾且非对称”的特点。

2.VaR 法只能测算正常情况下金融资产的价格波动率，却无法准确反映极端或者严重危机情况下金融资产的波动。Artzner 等[19]认为VaR 法只是提供了一个收益率尾部数据，并未对尾部损失进行深入研究，不利于测算极端情况下的波动率。据此他们提出了进一步改进方案——在损失大于特定VaR 值的情况下求解金融资产风险价值的ES法。魏宇[20]也通过实证论证了在极端波动情况下，极值理论（EVT）对于刻画金融资产收益率尾部分布情况更加准确。

3.VaR 法是以历史数据为依据预测未来的盈利和亏损，并假设过去因素的关系是恒定的，这与实际情况不符。赵岩、李宏伟和彭石坚[21]利用贝叶斯MCMC方法，将历史数据的先验信息和样本数据结合，作为后验信息估计模型中的未知参数，从而估算VaR值。

4.VaR 法不具有次可加性。Artzner 等[19]运用数学模型推导出VaR法不满足一致性原理，尤其是只有单调同可加性。林辉、何建敏[22]指出VaR 法限制了最小风险组合的求得。

目前VaR 模型被广泛应用于金融机构的投资组合、风险度量、绩效度量、头寸管理、风险预估和控制等领域。例如，宋逢明、谭慧[23]将内生和外生流动性放入传统VaR风险度量框架中，并以沪深样本数据为基础进行实证检验，结果证明考虑了流动性的VaR 模型比传统VaR 模型更有利于准确衡量股价波动性。

（二）ARCH模型

由于资产价格的波动容易受利率、汇率、财政政策、市场内外部消息等外在因素的影响，因此股票样本扰动项的方差大小依赖于前期误差的变化。传统的VaR模型假定股票收益率序列独立同方差，波动率不变，并没有体现出收益率序列的时效性，所以不能有效刻画实际金融市场的波动特征。基于此，1982年Engle[8]最先提出了一个自回归条件异方差ARCH模型。ARCH模型中添加了长期平均波动率及其权重，以显示主体的波动性随时间而变化。ARCH模型表达式如下：

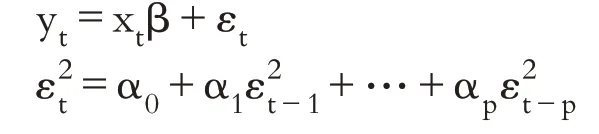
其中：yt为白噪声，是t期的被解释变量，由解释变量xt来解释；εt是t 期的扰动项，表示偶发因素的作用。该模型表示，扰动项εt的平方之间存在相关性，并且可以由p阶自回归式表示。

ARCH模型演进脉络如表3所示。

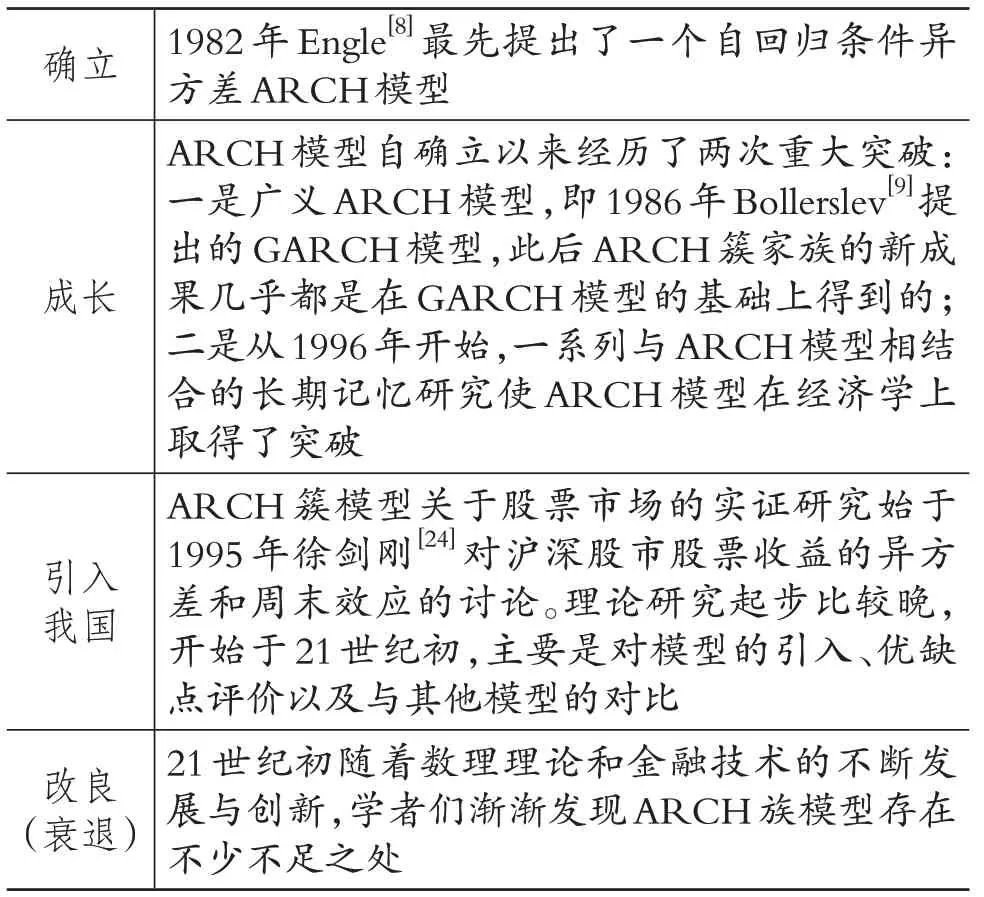
表3 ARCH模型演进脉络

在ARCH模型的成长时期，学者们对ARCH簇模型进行了创新性拓展，并取得了两次重大突破。一是1986年Bollerslev[9]将其拓展为GARCH 模型，并增加了干扰项条件方差的滞后期。其他的拓展模型还有VARCH、门限ARCH、因子ARCH 模型等。自GARCH 模型产生以来，ARCH 簇家族的新成果几乎都是在GARCH 模型的基础上形成的。二是自1996年初，一系列与ARCH模型相结合的长时记忆研究使得ARCH 模型在经济学上取得了突破。ARCH 簇模型由于良好的统计特性和能够对金融资产收益波动率进行准确刻画，而被应用于对经济类时间数据的研究中。

我国对ARCH 簇模型的理论研究建立在国外学者的研究成果上，主要是对模型的引入、优缺点评价以及与其他模型的对比。如：张世英、柯珂[25]对ARCH 模型进行了总结和分类，以探讨长记忆ARCH模型的性能。我国对ARCH簇模型的股市实证研究始于1995年徐剑刚[24]关于沪深股市股票收益的异方差和周末效应的探讨。丁华[26]指出，1994～1997年间的上证综指收益率序列明显存在自回归条件异方差现象，他利用ARCH模型发现股价波动呈集聚现象，波动是平稳的，另外，上证A 股市场是弱有效的。

异方差ARCH模型不仅模拟样本序列的方差，而且重点关注过去价格对当前股价的影响。此外，该模型还反映了股票收益“波动集聚”现象，这已被广泛认可。钱争鸣[27]通过数学分析得出，ARCH 模型的摄动项服从宽尾的正态分布序列，恰好符合股票收益的广尾分布特征，而且研究结果表明，过去的收益率不影响未来的收益率，这对应了有效市场假说。实务界应该推动ARCH 模型对我国投资与管理主体、研发主体的指导作用。

但是，随着数理理论和金融技术的不断发展与创新，ARCH 模型被发现存在以下四个不足之处：一是ARCH模型难以进行模型设定检验。如柯珂、张世英[28]认为ARCH 模型在模型设定检验方面存在障碍，线性回归模型的诊断分析方法不适用于ARCH模型。二是ARCH模型不适用于描绘极端情况下的股价波动情况。根据ARCH 模型可知，当某一期出现异常收益时会使得下一期条件方差的波动增大，所以通过该模型得出的波动率参数不稳定，容易产生误差。三是ARCH模型假定正向和负向的冲击对金融资产价格波动的影响程度是一致的、对称的，这不符合金融市场实际情况。四是ARCH模型的条件方差方程取决于自回归阶数，若要提高风险度量的准确性，就需要提高自回归阶数，这就大大增加了参数估计的难度，并且降低了风险度量的准确性。田原珺[29]认为ARCH 模型的缺点表现为：一方面，残差平方的滞后阶数难以确定；另一方面，如果考虑所有滞后平方的影响会将滞后阶数推到更大，模型更加复杂。

（三）GARCH模型

1986年Bollerslev[9]对ARCH模型进行拓展，提出了GARCH（1，1）模型。严格来说GARCH模型属于ARCH 簇模型，本应该归为一类讨论，但由于GARCH 模型自身也有很多拓展和改进形式，致使GARCH簇模型也成了一个内容丰富的分支。此外，GARCH 模型现已成为度量股市风险最常见的模型之一，地位重要，所以本文对GARCH簇模型进行单独探讨。依据相关文献，标准的GARCH（1，1）模型如下：

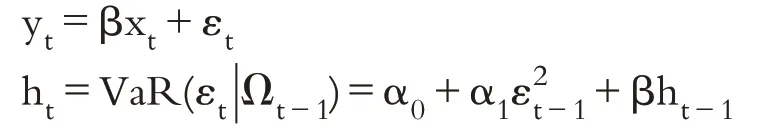
其中，yt是因变量，xt是解释变量的向量，β是未知参数的向量，α0、α1和β是待估参数。该模型假定εt在给定（t-1）时间内的信息Ωt-1满足正态分布，即：GARCH 模型考虑了两个不同的假设：一是条件均值；二是条件方差。上述模型的前一方程是均值方程，它是具有残余项的外生变量的函数，后一方程是条件方差方程。

GARCH模型演进脉络如表4所示。

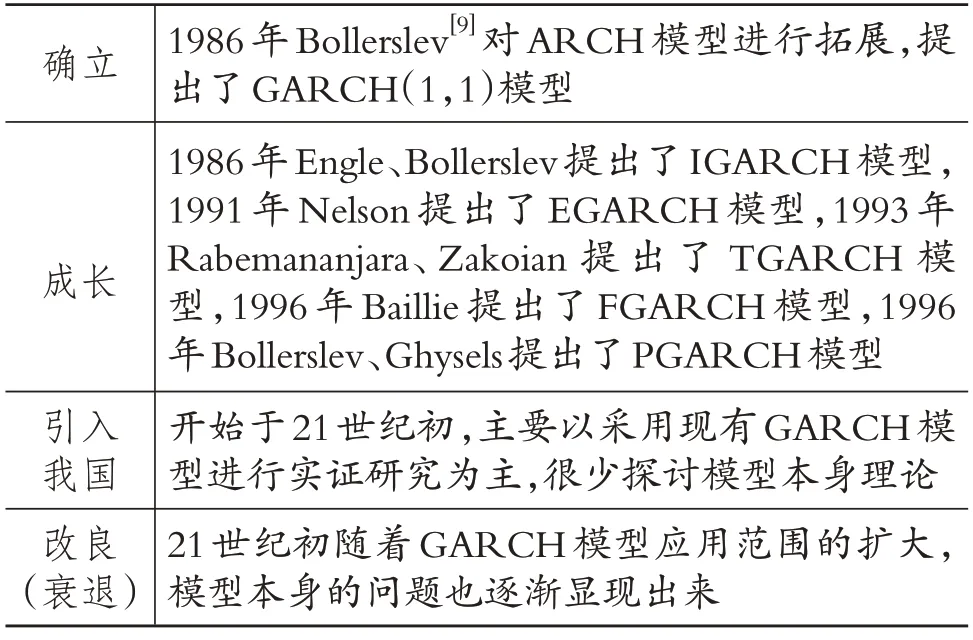
表4 GARCH模型演进脉络

自20世纪90年代以来，已有学者对GARCH模型进行了改进，并推出了一系列新模型。例如，1991年Nelson 分析了1962～1987年美国股票指数样本，发现了股票收益的非对称性，并提出了EGARCH 模型，放松了对参数非负性的约束。反映价格波动的不对称杠杆效应的另一个模型是在1993年由Rabemananjara、Zakoian 提出的TGARCH模型。1996年Baillie 探讨了序列变动异方差性和持续变动性，并提出了FGARCH 模型。同年，Bollerslev、Ghysels 提出了PGARCH 模型，该模型考虑的因素比较多，也被看作是其他GARCH模型的综合。与GARCH模型相比，PGARCH模型去掉了对模型方差的幂为2的限制，使方差更具有动态性，可以更好地刻划股市的杠杆作用。

对多元ARCH模型的研究兴起于20世纪90年代末。最早是在1998年Bollerslev等学者提出了适用范围最广的VECH 模型，但由于该模型中参数太多，不利于模型的估计，因此学术界便开始探讨简化的多元ARCH 模型。其中具有代表性的模型包括Bollerslev 提出的Constant Conditional Correlation模型、Engle R.F.提出的Dynamic Conditional Correlation 模型，以及Engle R.F.和K.F.Kroner 提出的BEKK 模型等。由于包含大量参数估计的算法可行性较低，所以目前多元ARCH模型的应用范围不是很广。

对于GARCH 模型，国内学者主要采用现有模型进行实证研究为主，很少探讨模型理论本身。陆蓉、徐龙炳[30]采用EGARCH模型，实证研究牛市和熊市对中国股市波动不平衡的影响。研究结果表明，股市在牛市阶段的信息不对称效应反映了显著的正回报效应，而熊市为显著的负面影响效应。在多元GARCH 模型方面，因为理论尚未成熟且没有方便计算的操作软件，国内虽然有相关的文献研究，但数量不多。

GARCH 模型除了和ARCH 模型一样具有异方差和自回归特性，还考虑了扰动项条件方差的滞后期，这使得该模型能排除过度的峰值，在计算股价（收益率）波动上有一定的优越性。邹建军、张宗益和秦拯[31]统计了1997年10月至2001年2月上海证券市场的日收盘价格，采用GARCH（1，1）模型、VaR模型和EWMA 模型衡量股票价格波动性，发现GARCH（1，1）模型最能反映上海证券市场的股票价格风险。

尽管采用GARCH模型得出的预测值能较好地拟合股票市场收益率序列，但该模型也存在一些不足之处：

第一，GARCH模型在刻画收益率序列“尖峰肥尾”“杠杆效应”“自回归平方序列持久而微弱”等特征时不是很显著。Jonas Andersson[32]认为GARCH模型对股票市场收益率序列“尖峰肥尾”“微弱但持续的自相关性”等特征刻画得不够明显。余素红、张世英和宋军[33]指出反映股价收益率序列“尖峰肥尾”特征的指标是高k 值，体现其“微弱但持续的自相关性”的指标是低φ值，但GARCH 模型的k 值直到φ值大于0.3以后才有增长趋势。另外，GARCH观测值高估了市场风险。

第二，和ARCH簇模型自带弱点相同，GARCH模型的方差被确定为先前观察的方差和之前扰动项条件方差的函数，因此异常观测值的存在会导致GARCH 模型估计的波动率序列不太稳定。即在异常情况下根据该模型得出的波动率参数容易产生较大的误差。

第三，由于不同GARCH 模型的假定条件和参数不同，适用的情境也不同，故对风险预测和管理的有效性也会有所区别。陈守东、俞世典[34]通过实证研究得出，t 分布和GED 分布假定下的GARCH 模型比正态分布下的GARCH模型能更贴合地反映金融资产价格波动情况。

（四）极值模型

自20 世纪70年代以来，随着金融市场的全球化、衍生化、自由化，一些极端金融风险的爆发变得更加频繁，金融市场的风险管理者和投资者对金融资产收益率的异常波动尤其敏感，极值理论开始得到重视。

极值类型定理（Fisher-Tippett）：设x1，…，xn是独立同分布的随机变量序列，如果存在常序列{an＞0}和{bn}，使得H（x）成立，其中H（x）是非退化的分布函数，那么H必属于下列三种类型之一：

Ι类分布（Gumbel分布）：

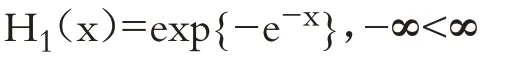
Ⅱ类分布（Fréchet分布）：

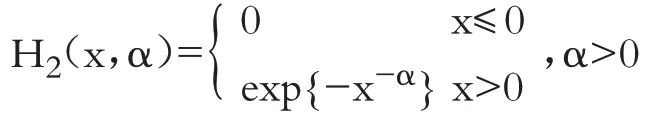
Ⅲ类分布（Weibull分布）：

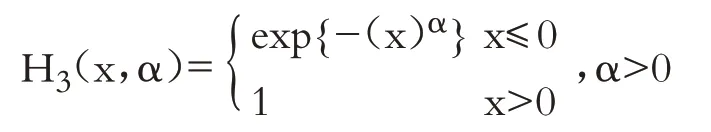
上述三类分布统称为极值分布。当α=1 时，H2和H3分别被称为标准Fréchet 分布和标准Weibull分布。称an、bn为规范化常数。在上述三类极值分布中，大多数金融资产收益率波动服从Fréchet 分布，Fréchet 分布具有与金融资产收益率序列“尖峰肥尾”特征相拟合的统计特性。

从上述公式可以看出，运用极值模型衡量股市波动风险应注意两个方面：一是目标变量的特定统计特征；二是目标变量的极值分布形态。

极值模型演进脉络如表5所示。

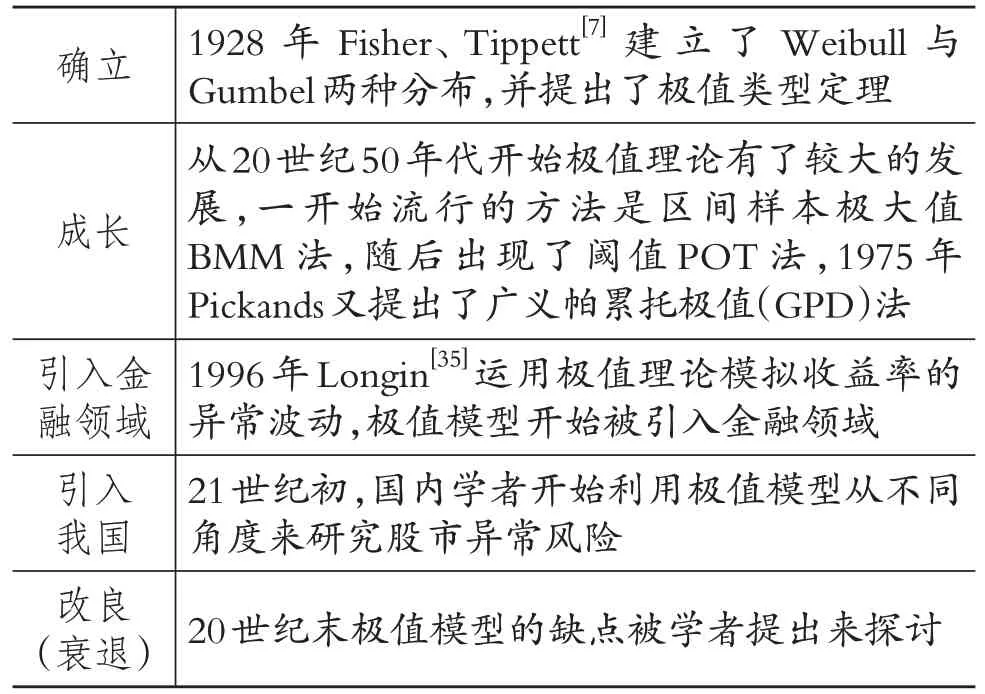
表5 极值模型演进脉络

1928年Fisher、Tippett[7]构建了Weibull与Gumbel的两种分布，并提出了极值定理。1943年Gnedendo严格证明了极值定理：极值的极限分布与其本身分布是相互独立的。因此，在总体分布未知的情况下，可以从样本分布中得到整体极值的分布，并可以准确估计金融市场资产收益率的尾部损失。

自20世纪50年代以来，极值理论取得了重大进展。第一种流行的方法是区间样本极大值BMM 方法。随后出现了阈值POT 法。1975年Pickands 首次提出了广义帕累托极值（GPD）方法。极值理论一开始应用于水利学研究，之后被引入金融领域。Longin[35]将1885～1990年美国股市的日收益进行整理，并将统计学中的极值理论应用于模拟收益率的异常波动。Dowd[36]在1998年提出仅对金融资产收益率尾部超过一定阈值的数据建模的极值模型。Diebold、Schuermann 和Stroughair[37]将极值理论引入金融风险管理领域。

21世纪初，国内学者开始利用极值模型从不同角度来研究股市异常风险。封建强[38]运用极值VaR方法测度沪深股市收益率的波动风险，同时比较了极值法、半参数法和传统VaR 法的测量效果。黄大山等[39]通过对极值POT 方法建模的实证研究，指出深圳股票指数不符合正态分布，并且有明显的厚尾特征。

极值理论有两个分支：一是BMM（Block Maximam）分支，它将分割后具有明显季节特征的样本数据进行极值建模，对应于广义极值分布GEV 模型；二是阈值POT（峰值超过阈值）分支。BMM 法选择分区之间的数据并仅选择区间的最大值，但如果区间的次大值比其他区间的最大值大，就会浪费大量数据并加大参数估计的不确定性。一般情况下，GPD模型所需的样本量要大于GEV模型，适用范围更广。

极值模型不关注收益率序列的整体分布，无需提前假定特定的模型，而是根据样本数据自身分布去研究极端值的分布情况，从而分析总体中极值的变化。该模型能依据样本很好地估计总体，是一个强大的分位数预测工具。极值模型在研究异常市场波动方面具有优势，所以经常被用于异常情况下股市价格分析以及其他资产的极端价格分析。一开始极值模型主要被应用于外汇市场研究，后来由于保险巨额赔偿事件时有发生，该模型也被应用于保险索赔定价领域。

极值模型虽然适用于股票收益率序列肥尾分布的研究，但也存在两个缺点：第一，极值模型的前提假定是股票收益率序列是独立同分布的，但实际上大多数金融资产具有相依性。如果我们仅仅使用极值模型，就无法描绘新消息冲击对收益率的影响。因此，可以考虑将极值模型样本独立同分布的假定条件放松或者进一步改进，以匹配实际股票市场数据。第二，由于静态的极值模型仅研究静态的金融资产尾部收益率分布，不利于分析收益率序列波动率动态变化的特征，没有时效性。极值模型的缺点在20世纪末就已被学者提出来探讨，如1998年Peter、Diebold和Til[40]分析了极值理论的优点、缺点及应用范围。

为了更准确地预测和管理金融资产的价格波动，学界经常将极值理论与其他模型相结合使用。第一种是将极值模型与GARCH 模型组合。例如，Embrechts、McNeil 和Straumann[41]指出极值模型有利于研究股票收益率序列的尾部损失分布，GARCH 模型善于捕捉波动率的动态变化特征，所以可以将极值模型与GARCH 模型组合。第二种是将极值模型与Copula模型组合。第三种是将极值模型与其他模型组合。

（五）SV模型

SV模型直接关系到金融资产定价的扩散过程。学界对SV模型有不同的分类。1973年Clark[10]首先提出了金融资产收益率的时变波动SV 模型。1986年Taylor在其著作《Modeling Financial Times Series》中解释金融收益序列波动模型的自回归行为时，提出了离散时间SV（SV-N）模型。Hull 和White[42]、Meline 和Turnbull[43]在研究期权定价时，探讨了一种服从Ornstein-Unlenbeck 随机过程的连续时间SV 模型。学界一般针对SV-N 模型展开研究，具体模型如下：

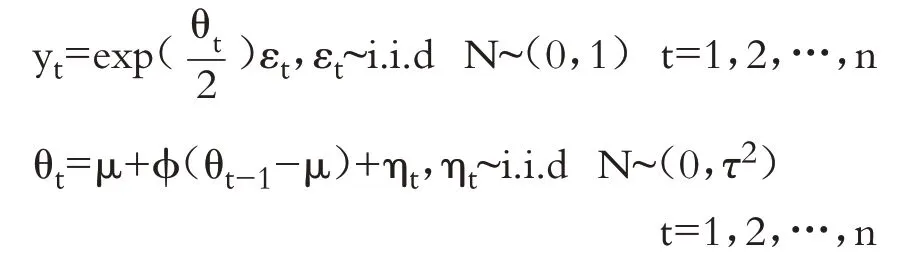
其中：yt表示第t日的收益率；εt为独立同分布的白噪声干扰，服从均值为0、方差为1的正态分布；ηt为独立同分布的波动项的扰动水平，服从均值为0、方差为τ2的正态分布。误差项ηt和εt是不相关的，都是不可观测的。持续性参数ϕ反映了当前波动对未来波动的影响，并且对于|ϕ|＜1，SV模型是协方差平稳的。潜在的波动θt服从一个持续性分布为ϕ的高斯AR（1）过程。

SV模型演进脉络如表6所示。

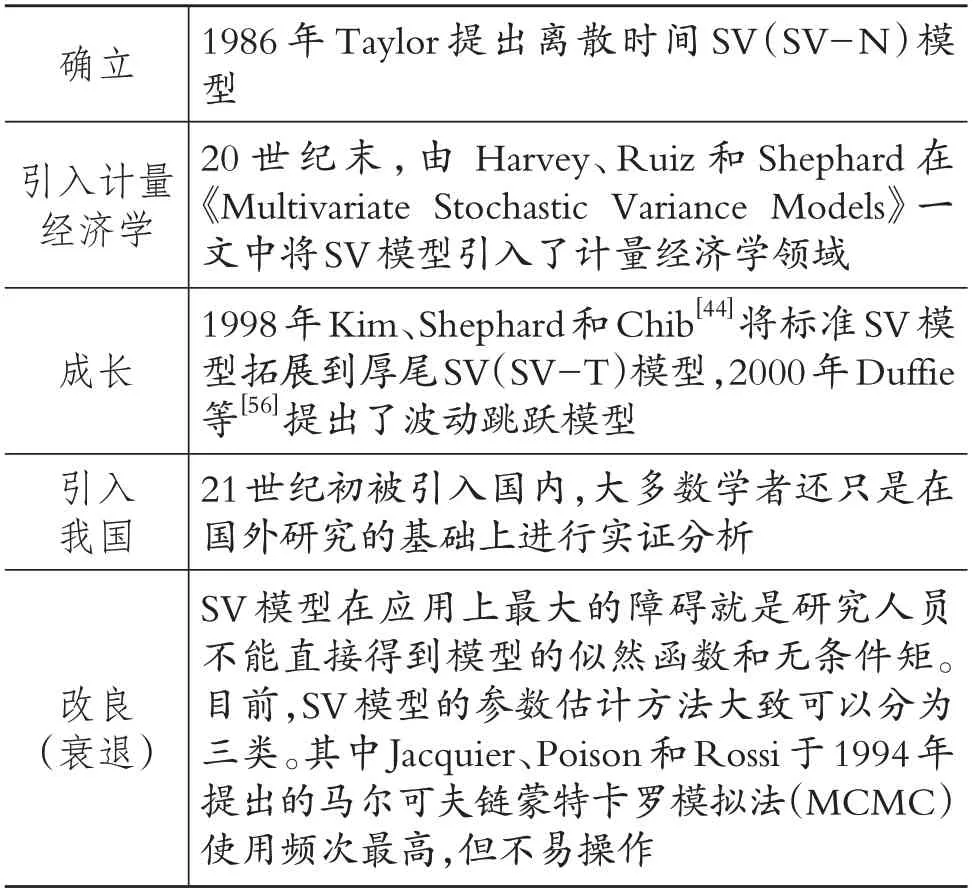
表6 SV模型演进脉络

SV 模型自提出后学者们也在不断地对其进行扩充和改进。如Kim、Shephard 和Chib[44]将标准SV模型拓展到厚尾SV（SV-T）模型，厚尾SV模型更加细致地刻画了金融资产价格波动的“胖尾”特征。为了使SV模型能够被更有效地运用于金融市场分析，Duffie 等[45]提出了波动跳跃模型，该模型表明外在因素的冲击往往会使得实际股价出现大幅度变化，即收益率序列中会出现“跳跃现象”。Eraker、Jobannes和Polson[46]通过对股价样本数据的实证分析，同样证明在SV模型中加入跳跃项能更有效地拟合实际股票市场收益率序列。

21 世纪初，SV 模型被引入国内，大多数学者还只是在国外研究的基础上进行实证分析。如白崑、张世英[47]构建了一阶扩展SV 模型，并对深圳证券交易所指数样本数据进行了实证分析，发现扩展SV模型更能拟合实际股票市场“波动积聚”和“持续波动”的特征。

计量学者和金融学家认为，由于SV模型的波动率分布是一个不可观测的随机过程，独立于过去观测值，因此，它似乎更加稳定，更适合捕捉金融资产价格波动的特征。同时SV 模型对收益率序列的“尖峰肥尾”特征刻画得更加准确。余素红、张世英[48]通过对上海证券交易所和深证证券交易所抽样数据的实证检验证明，SV-AR 模型的VaR 比GARCH（1，1）更符合实际情况。因此，使用SV 模型有助于找到我国股市的潜在规律。孟利锋、张世英[49]运用非线性SV模型对上证综指和深证成指进行样本检验，研究发现，两者的收益率序列存在明显的杠杆效应，即股价的下降会导致未来波动的上升，并且上海股市的表现要比深圳股市更稳定。

由于SV 模型分别非正态，方差不能直接观测，因此研究人员无法直接获得SV 模型的似然函数和无条件矩，使得该模型的实际操作难度增加，这也是SV模型在应用上最大的障碍。目前，SV模型的参数估计方法大致可以分为以下三类：一是使用传统的近似或者模拟方法构造参数，如Harvey、Ruiz 和Shephard 提出的伪极大似然法（QML）；二是引入一个辅助模型或者半参数法；三是利用贝叶斯原理进行参数后验分布分析。其中Jacquier、Poison 和Rossi于1994年提出的马尔可夫链蒙特卡罗模拟法（MCMC）使用频次最高，但是该方法对研究人员的能力要求高，所使用的计算软件也要非常规范，所以现实中不易操作。

（六）Copula模型

由于多元正态分布是没有尾部依存关系的，但在实际情况下金融资产之间存在相关性。金融资产之间的相关性是影响投资组合的一个重要因素。基于此，1959年Sklar[4]通过定理形式提出Copula这个概念，之后在国外得到迅速发展并应用于金融管理、投资组合分析等领域。

Sklar 定理：令F 为具有边缘分布F1（x1），…，Fn（xn）的联合分布函数，那么存在一个Copula 函数C，满足：F1（x1，…，xn）=C（F1（x1），F2（x2），…，Fn（xn））。若F1（x1），…，Fn（xn）连续，则C唯一确定。

Copula模型的演进脉络如表7所示。

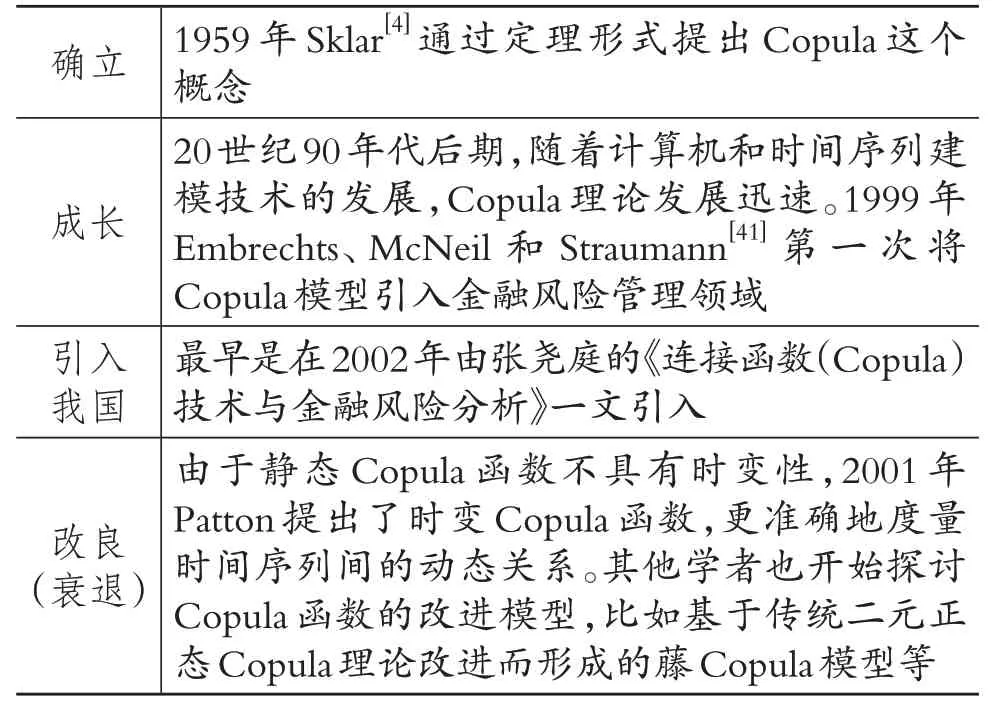
表7 Copula模型演进脉络

20 世纪90年代后期随着计算机和时间序列建模技术的发展，Copula 理论发展迅速。1998年Nelson 在其著作《An Introduction to Copulas》中系统地引入了Copula 理论，将n 元变量的联合分布分解为一个Copula 函数和n 个边缘分布，指出Copula函数在描绘金融资产的相关性中起到重要作用。Embrechts、McNeil 和Straumann[41]将Copula 模型引入金融风险管理领域。还有一些学者专门介绍了Copula 函数的参数估计方法和半参数估计方法，以及Copula模型的检验方法。

国内学者对Copula模型的研究相对落后，最早是在2002年张尧庭研究金融风险时将该模型引入我国。一般都是学习国外的研究，然后将其运用到我国的实际情况中，进行一些实证分析。

Copula 函数主要分为椭圆函数族和阿基米德Copula 函数族两个分支。其中，椭圆函数族包括正态Copula 函数和t-Student Copula 函数。虽然二元正态Copula函数可以更好地拟合股票市场数据，但是其不能显著反映真实股票市场的非对称相关性，而且不能反映极值条件下股票市场尾部相关性增强的规律，往往会低估风险。与二元正态Copula 函数不同，t-Student Copula 函数的尾部相关系数会随着自由度的增加而增加。阿基米德族Copula包括Gumble Copula、Frank Copula 和Clayton Copula。Gumble Copula 的密度函数是不对称的，其密度分布上尾高下尾低，因此在捕捉顶部变量的变化时是非常快速和有效的，可以用来描述具有上尾相关性特征的股票市场（牛市）的相关性。Frank Copula 的密度分布是对称的，不管是正向还是负向的冲击，只要带来的收益绝对值相同，则收益率序列的相关关系就是相同的，然而实际上这并不准确。Clayton Copula 可以看作是Gumble Copula 函数的反函数，适合于刻画具有下尾相关性特征的股票市场（熊市）的相关性。

Copula 模型的优点主要包括以下两个方面：第一，它是一种研究相互依赖关系的方法，能综合描述所有金融资产的非线性相关性。第二，作为构建二维分布族的起点，Copula 模型可以用来构造多元模型分布和随机模拟，并分别分析边缘分布和相关性，因为它不受边缘分布选择的限制。陈守东、胡铮洋和孔繁利[50]的实证结果表明Copula 拟合效果优于正态VaR，其中Gumble Copula 在Copula族中表现最佳；另外，将t 分布作为实验的边缘分布能加强对股票数据的模拟效果。

尽管Copula 函数可以全面地涵盖金融资产间的相关性，但是它没有考虑大多数建模情况下边缘分布的不对称性，而且静态Copula函数不具有时变性。基于此，Patton 于2001年在其论文《Modelling Time -varying Exchange Rate Dependence Using the Conditional Copular》中提出了时变Copula 函数，并指出时变Copula函数能够更准确地度量时间序列之间的动态关系。另外，传统的二元正态Copula理论对股票市场投资组合中多元化股票之间的相关结构刻画得不够准确细致，建议使用改进后的藤Copula模型。

在理论层面，目前学界越来越关注Copula模型的动态研究。因为实际的金融市场瞬息万变，尤其是股价的波动率对内外部环境变化的敏感程度是非常高的。因此，动态Copula 模型通常用于分析不同金融市场的风险溢出效应和时变性。Patton[51]首创性地提出了动态Copula函数，并在2004年实证研究发现，动态Copula模型在建模时其参数会随着时间产生变化。

动态Copula 模型在金融领域运用最广的方面包括：①金融市场动态关联分析方面。叶五一、谭轲祺和缪柏其[52]以2006年1月4日至2016年7月1日的28 个股票市场行业日收益率为基础，运用动态Copula 模型分析行业之间的系统性风险及风险溢出效应。②金融市场的定价方面。2003年Goorbergh、Genest 和Werker 在《Multivariate Option Pricing Using Dynamic Copula Models》一文中第一次将动态Copula模型运用于多元期权定价中。③金融风险管理与防范方面。学者主要关注金融危机的传染效应和投资组合的风险管理。刘平、杜晓蓉[53]采用静态和动态Copula 模型相结合的方法，对1997年和2007年中美三个金融市场之间的相关关系进行分析，并且对比股市风险的风险传染效应和传染途径，发现2007年中美市场的关联性大幅度上升，存在传染效应。由于1997年之后，中美经济联系明显增强，所以美国金融危机对我国的破坏程度也会加大，主要通过国际金融和国际贸易渠道传染风险。

在实务层面，Copula 模型最先被引入金融市场风险管理领域。Hu 等[54]使用Copula 函数测试多个金融市场的相关性。Cherubini 等[55]在计算投资组合在险价值时运用了Copula函数。吴鑫育等[56]研究发现，我国股票市场收益率的杠杆效应具有非对称性和时变性，随机Copula方法适用于研究收益率序列的杠杆效应。此外，Copula 模型还能运用于信用风险和操作风险度量、衍生品定价等领域，也能帮助多学科的发展。如CSFB（Credit Suisse First Boston）开发的Credit Risk 和J.P.Morgan 开发的Credit Metrics都直接或间接地利用了Copula模型。Genest、Quessy和Remillard[57]统计发现，Copula模型在工程学、生物统计学、经济学、金融学等多学科领域应用成果丰富。

（七）模型优缺点对比

根据上文对六个模型相关的理论及实证文献的整理分析，总结各个模型的优缺点如下：

1.风险价值法（VaR）。优点包括：①否定了风险与收益呈线性关系的假定，真正反映了随机过程；②方法简单，用一个指标综合反映金融市场的不同风险，可以用于对股票市场资产组合整体性风险的前瞻性分析。

缺点包括：①VaR 分布呈正态性，不能有效刻画实际股票市场收益率序列呈现的“尖峰肥尾”特征；②无法解决极端或者严重情况下（如股票崩盘）股价的波动率；③以历史数据预测未来损益，并且假定过去因子的关系恒定不变，与实际不符；④一致性原理并未得到满足，尤其是次可加性，这限制了最小风险组合的求取。

2.ARCH模型。优点包括：①考虑了利率汇率、财政政策等外在因素对股票市场波动的影响，对样本序列的方差进行建模，关注到前期价格对当前股价的影响，体现了序列相关性；②刻画了股票收益率序列的“波动集聚”现象。

缺点包括：①难以进行模型设定检验；②条件方差和过去观测值直接相关，极端情况下测得的股价波动率不稳定，也会降低对长期波动预测的准确性；③不能表现实际股票收益率序列的不对称性；④条件方差方程取决于自回归阶数，若要提高风险的准确性，就需要提高阶数。

3.GARCH模型。优点为：GARCH模型还考虑了扰动项条件方差的滞后期，这有助于排除过度的峰值。到目前为止，GARCH模型仍然是金融风险预测和管理领域最常用的模型。

缺点包括：①在刻画收益率序列“尖峰肥尾”“杠杆效应”“自回归平方序列持久而微弱”等特征时不是很显著；②条件方差和过去观测值直接相关，极端情况下测得的股价波动率不稳定，会降低对长期波动预测的准确性；③设定不同的假定条件和参数会影响风险预测的准确性和管理的有效性。

4.极值模型。优点包括：①能对金融资产收益率的尾部数据进行精确的估算，可以解决极端情况下（如股价崩盘）的价格变化问题；②由样本估计总体，可以不关注收益率序列的整体分布，无需提前假定特定的模型，根据样本数据自身分布去研究极端值的分布情况，从而分析总体中极值的变化。该模型是一个有效的分位数预测工具。

缺点包括：①模型的前提假定是股票收益率序列是独立同分布的，但实际上大多数金融资产具有相依性，如果仅仅使用极值模型，将无法准确描绘新消息对收益率的影响；②静态的极值模型仅研究静态的金融资产尾部收益率分布，不利于分析收益率序列波动率动态变化的特征，没有时效性。

5.SV模型。优点包括：①SV模型的波动率分布是一个独立于过去观测值的不可观测的随机过程，因此该模型似乎更稳定，而且更适合捕捉金融资产价格波动特征；②更能捕捉收益率序列的“尖峰肥尾”特征。

缺点为：SV 模型是非正态分布，方差不能直接观测，这增加了模型的操作难度。

6.Copula 模型。优点包括：①实际股票收益率序列分布是具有尾部相依性的，Copula 模型是一种研究相依性的方法，较为全面地描述了所有金融资产非线性的相关关系；②Copula 模型作为构建二维分布族的起点，由于不受边缘分布选择的限制，可以用于构建多元模型分布和随机模拟，将边缘分布和相关关系分开分析。

缺点包括：①在大多数建模情况下都没有考虑到边缘分布的非对称性；②静态Copula函数不具有时变性；③传统的二元分布Copula理论对股票市场投资组合中多元化股票之间的相关结构刻画得不够准确细致。

五、总结

通过阅读大量关于股票市场风险度量的文献，并对其进行归类分析后，笔者发现VaR 模型、ARCH 模型、GARCH 模型、极值模型、SV 模型和Copula 模型六种模型都是起源于西方发达国家。目前国内学者对这六种模型的研究大多数是基于现有的模型理论，对某一时间段的上证综指或深证成指的收益率数据作实证研究，或者比较不同模型在衡量股价波动性方面的有效性。也有一些国内学者根据我国实际情况，对现有模型做出调整参数的改进，或者对多个模型进行组合应用于实务研究，但是基本没有涉及模型根本因子的变动或者提出首创性的风险测度模型。

VaR 模型测算方法简单，适用于正态分布下股票收益率极端风险的测度。但其受正态性所限，无法精确描绘现实股市“尖峰肥尾、波动集聚”等波动特点。目前国内学者对传统VaR模型的理论研究已经不多，主要聚焦于改进VaR模型以及将其运用于非金融领域。

ARCH簇模型（含GARCH模型）可以针对“波动集聚”分布下的股票收益率风险进行测度，其中GARCH 模型表现更优，因为该模型能够排除过度的峰值。但是ARCH簇模型由于条件方差和过去观测值直接相关，因此在极端情况下使用该模型测得的股价波动率不稳定，这会导致对长期波动预测的准确性降低。国内学者对ARCH簇模型的关注重点在于利用GARCH 改进模型（如ARMA-GARCH模型、GARCH-SVM 模型等）对货币市场、债券市场以及股票市场进行实证研究。因此，笔者建议国内学者多关注GARCH 模型理论本身，例如多元GARCH理论。

极值模型适用于分布未知情况下对股票收益率尾部分布状态的估计。该模型通过分析样本数据尾部损失估计总体尾部分布，有利于对极端情况下（如股市崩盘）的股价波动性进行研究。但是极值模型没有考虑到大多数金融资产之间的依赖性特点，该模型目前主要应用于研究外汇市场和成熟金融市场的异常风险。基于此，笔者建议国内研究人员加强对利用极值模型分析新兴金融市场风险领域的理论和实务研究。

SV 模型适用于分布未知情况下的股票收益率风险测度，这种方法更灵活也更能捕捉收益率序列“尖峰肥尾”的特征，但是该模型在现实条件下的操作难度较大。目前国内学者主要关注SV模型在连续时间方面与期权定价理论、利率期限结构模型等金融理论模型的联系。近两年学者们开始研究带有随机波动的时变参数结构因子增强向量自回归（TVP-SV-SFAVAR）模型。事实上SV 模型还有其他可进一步探索的维度，如我国对已实现SV模型的研究还非常少见，这一方面有待加强。

Copula 模型适用于跨市场和跨股市下的股票收益率风险测度，然而该模型在大多数情况下忽略了边缘分布的非对称性。目前国内对于Copula模型的探讨集中于水利工程、银行理财、原油市场、股票市场风险度量等实务领域。根据前文的研究综述，笔者认为，在动态Copula 模型、藤Copula 模型等Copula改进理论层面，我国还有较大的研究空间。