不同冲击工况下蜂窝填充薄壁结构的耐撞性能

张 勇， 闫晓刚， 曾 意， 赖雄鸣

(华侨大学 机电及自动化学院， 福建 厦门 361021)

薄壁结构以其质量轻、吸能高等优点而被广泛用于汽车、高速列车、飞行器的吸能构件中.虽然薄壁空管能够吸收冲击产生的能量，但仍存在变形不稳定及易产生欧拉屈服的缺陷，从而导致其吸能性能降低[1-3].

近年来，新型多孔吸能材料——金属蜂窝引起了研究人员的广泛关注.早期的研究主要集中于蜂窝材料的面内和面外特性.El-Sayed等[4]对蜂窝面内方向的吸能性能进行了研究，并提出了耐撞性响应的预测公式；张新春等[5]研究了胞元对六边形蜂窝面内的冲击变形和吸能特性的影响，以及胞元的微结构和密度呈梯度变化的蜂窝面内的冲击性能[6-7]；刘颖等[8]研究了圆形蜂窝面内的冲击力与吸能特性；Tao等[9]通过实验和数值分析的方法研究了应变率对蜂窝材料面外冲击性能的影响；Xu等[10]和Khan等[11]通过实验研究了六边形蜂窝的结构尺寸及相对密度对其面外冲击性能的影响，发现蜂窝结构在面外方向的吸能性能优于其在面内方向的，并可用于薄壁结构的填充材料；Santosa等[12]研究了铝蜂窝填充管的轴向压缩耐撞性能，发现蜂窝填充薄壁结构的耐撞性能优于传统的薄壁空管；Guden[13]和Zarei等[14]发现，将铝蜂窝填充到薄壁空管后，不仅能够提高薄壁结构的耐撞性能，而且能够使其变形模式更加稳定；闫晓刚等[15]发现，环形蜂窝填充薄壁结构的耐撞性能优于中心填充薄壁结构；笔者的前期研究表明[16]，交错排布的三角形蜂窝填充薄壁结构具有更优异的动态力学性能.

然而，以上研究主要针对蜂窝填充薄壁结构的轴向且在低速冲击工况的耐撞性能，但实际交通事故皆是不同的冲击角度和冲击速度并存的复杂冲击工况.因此，本文提出了一种方形蜂窝填充薄壁结构，并在不同的冲击角度和冲击速度下研究其动态耐撞性，获得了不同冲击工况下蜂窝填充薄壁结构的最优设计参数.

1 蜂窝填充薄壁结构及数值模型

1.1 蜂窝填充薄壁结构

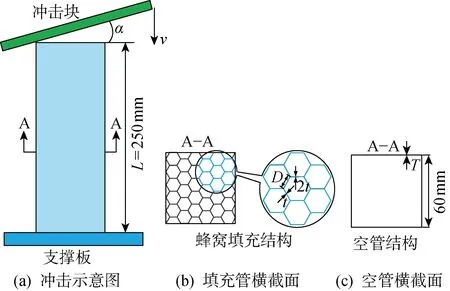
图1 蜂窝填充薄壁结构的几何模型Fig.1 Geometric model of honeycomb-filled thin-walled structures

图1(a)所示为不同的冲击角条件下蜂窝填充薄壁结构和薄壁空管结构的冲击过程示意图.其中，α为冲击角，表示冲击块平面法向与薄壁管顶端平面法向之间的夹角，蜂窝填充薄壁结构的底部固定在支撑板上.图1(b)为蜂窝填充薄壁结构的横截面及蜂窝芯的放大图，图1(c)为相应的薄壁空管的横截面.其中：蜂窝填充薄壁结构的长度L=250 mm，外管的横截面尺寸为60 mm×60 mm，薄壁外管的壁厚T=0.8 mm，蜂窝胞元的厚度t=0.05 mm，胞元边长为D=3 mm.

1.2 蜂窝填充薄壁结构的数值模型

根据图1的几何模型，利用LS-DYNA软件所建薄壁空管及蜂窝填充薄壁结构的有限元数值模型如图2所示.模型采用2 mm×2 mm的Belytschko-Tsay四节点壳单元进行离散，冲击块与薄壁管之间的接触定义为自动点-面接触，薄壁管自身的变形采用自动单面接触，薄壁管与蜂窝芯之间采用自动面-面接触，接触中的静摩擦系数与动摩擦系数分别设为 0.3 和 0.2.薄壁空管及蜂窝填充芯的材料均为铝合金AA6060，其密度为 2.7 g/cm3，弹性模量为 68.2 GPa，泊松比为 0.3，其应力(σ)-应变(ε)曲线如图3所示，且忽略应变率对铝合金材料动态冲击性能的影响[17].

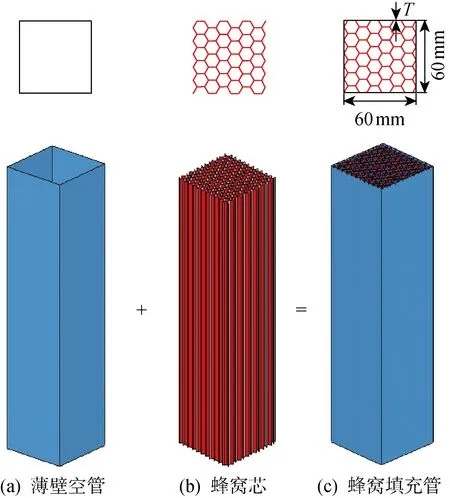
图2 蜂窝填充薄壁结构的数值模型Fig.2 Numerical model of honeycomb-filled thin-walled structures

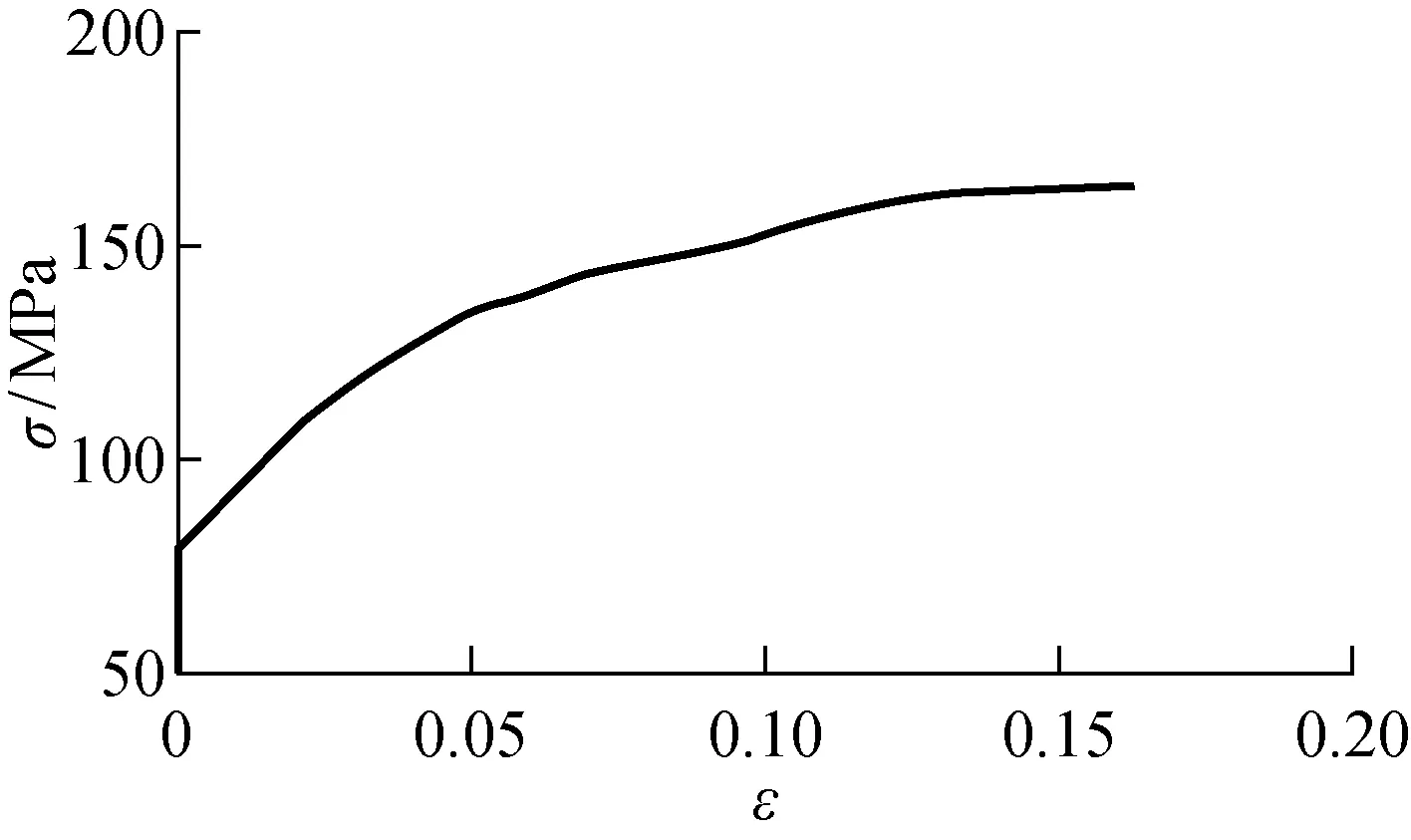
图3 铝合金AA6060的应力-应变曲线Fig.3 Stress-strain curve of AA6060 alloy

1.3 耐撞性能评价指标

在动态冲击过程中，以比吸能(SEA)和瞬时碰撞冲击力峰值(Fmax)作为耐撞性能评价指标.其中，SEA为单位质量所吸收的能量，即

(1)

(2)

式中：m为薄壁构件的总质量；Ea为吸收的总能量；d为碰撞吸能过程中的有效压缩位移，文中取管长的70%；x为压缩距离；F(x)为瞬时碰撞冲击力.

SEA值越大，表示结构的能量吸收能力越强，较高的Fmax值将会引起较大的减速度，从而导致严重的乘员伤害.因此，冲击过程中需确保Fmax在人体可承受的范围内[18].

1.4 有限元模型验证

为了确保数值分析中有限元模型的准确性，本文对蜂窝填充薄壁结构的有限元模型进行了实验对比研究.图4所示为蜂窝填充管的实验与模拟的结果对比.图4(a)为蜂窝填充薄壁结构的实验样品.实验过程：首先，采用锯切割铝外管，并对其端面进行磨平处理；将蜂窝填充芯用线切割的方法切割成合适尺寸并直接填充在外管中，薄壁外管的T=1.2 mm，蜂窝芯胞元的D=3.00 mm、t=0.05 mm；再将试件放置于MTS材料力学试验机的支撑板与压头之间，使压头以5 mm/min的速度压缩蜂窝填充管.同时，采用相同的约束和载荷边界条件建立实验样品的有限元数值模型，模型采用 0.5 m/s的加载速度以模拟实验的准静态压缩工况.图4(b)～(d)所示为3个压缩位移d的条件下蜂窝填充管的实验与有限元模型模拟的变形模式.由图4可见，蜂窝填充薄壁结构的模拟变形与实验样品的变形模式基本一致.表1列出了在不同压缩位移下有限元数值模拟和实验所得吸收能量的对比.可以看出，在不同压缩位移下实验与模拟所得吸收能量较为接近， 最大绝对误差约为8%.由此可见，本文建立的蜂窝填充薄壁结构的有限元模型具有较高的准确性.

图4 蜂窝填充管的实验与模拟的变形模式Fig.4 Deformation modes of experiment and simulation results for honeycomb-filled tube

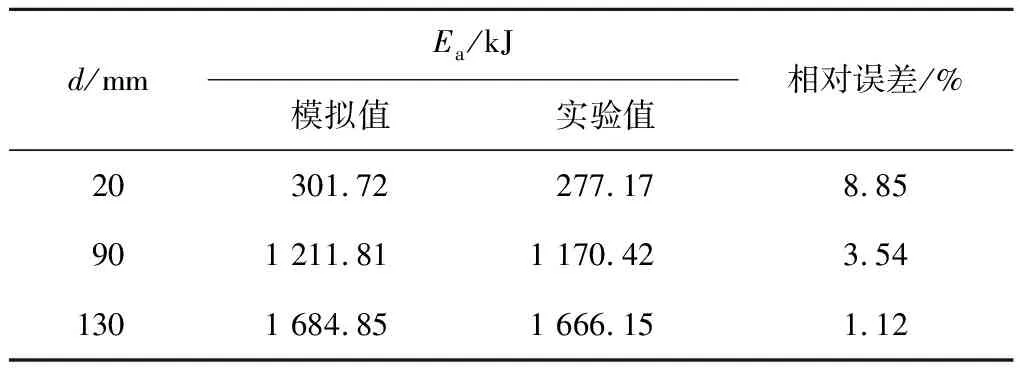
表1 实验与模拟结果对比Tab.1 Comparisons between simulations and experiments

2 蜂窝填充薄壁结构的耐撞性

为了研究蜂窝填充薄壁结构在不同冲击工况下的耐撞性能，根据图1的几何模型，本文探测了12种冲击工况下蜂窝填充薄壁结构及传统的薄壁空管结构的耐撞性响应.其中，包含了4种冲击角(α=0°，5°，15°，20°)和3种冲击速度，即v=30 km/h(低)，60 km/h(中)，100 km/h(高).图5示出了不同的冲击工况下薄壁空管和蜂窝填充薄壁结构的比吸能.由图5(a)可见，当冲击速度一定时，随着α增加，蜂窝填充薄壁结构和薄壁空管的SEA均逐渐降低，这主要是由于冲击角增大时，作用在薄壁结构上的横向弯矩逐渐增大，结构易发生全局弯曲而减小了轴向折叠次数.对于薄壁空管而言，当α从0° 变化为20° 时，SEA的降幅较为平稳，表明其在斜向冲击工况下的稳定性较好.相对而言，蜂窝填充薄壁结构在小角度冲击工况(α处于0°～15° 之间)下的SEA的降幅也较为平稳；但当α=20° 时，蜂窝填充薄壁结构的SEA出现了显著降低，其降幅最高可达 62.1%，表明蜂窝填充薄壁结构在大角度冲击工况下的稳定性较差.图6示出了在α=20° 的冲击工况下，薄壁空管与蜂窝填充薄壁结构在v=100 km/h和不同压缩距离时的变形模式.可以看出，蜂窝填充薄壁结构的底部出现了全局弯曲失稳的情况，从而导致其SEA大幅降低.

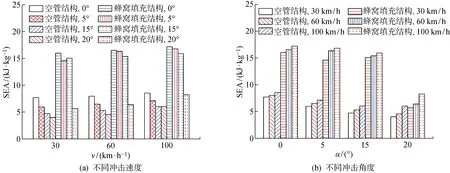
图5 不同的冲击工况下蜂窝填充管和薄壁空管的比吸能Fig.5 SEA of honeycomb-filled tubes and thin-walled hollow tubes under multiple impact loadings

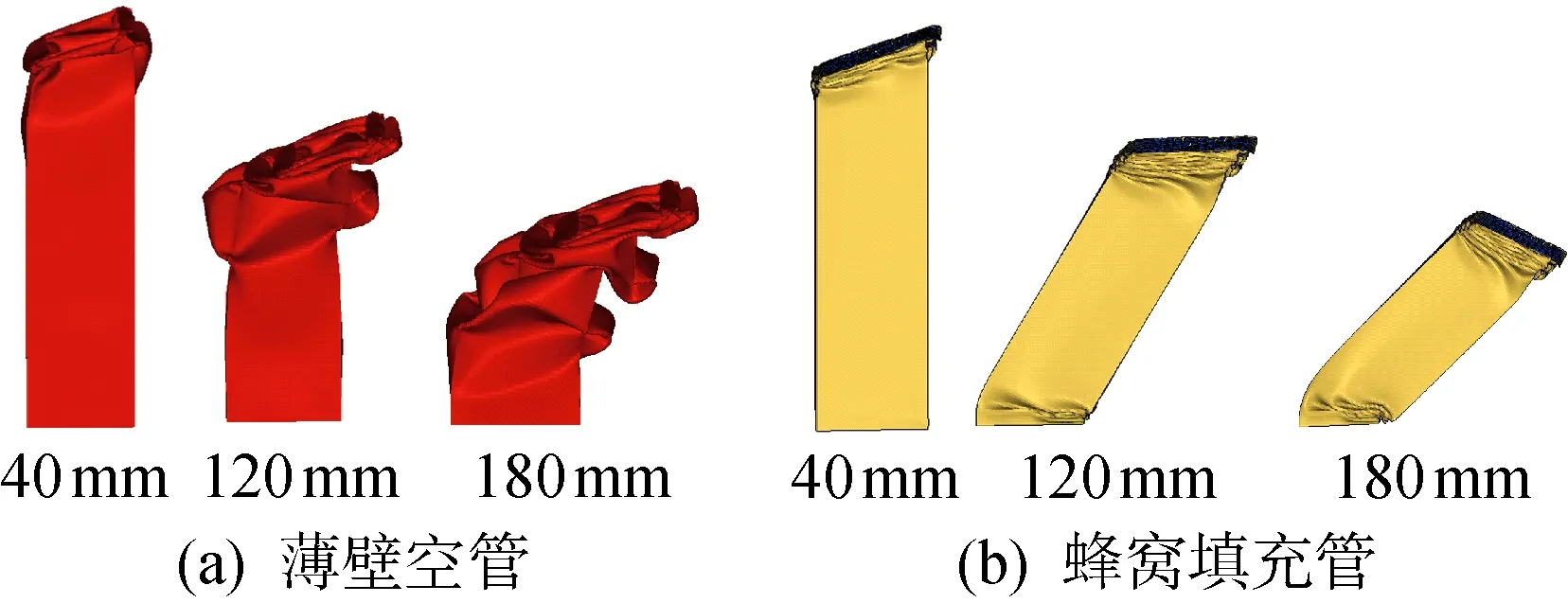
图6 薄壁结构的变形模式Fig.6 Deformation shape of thin-walled structures

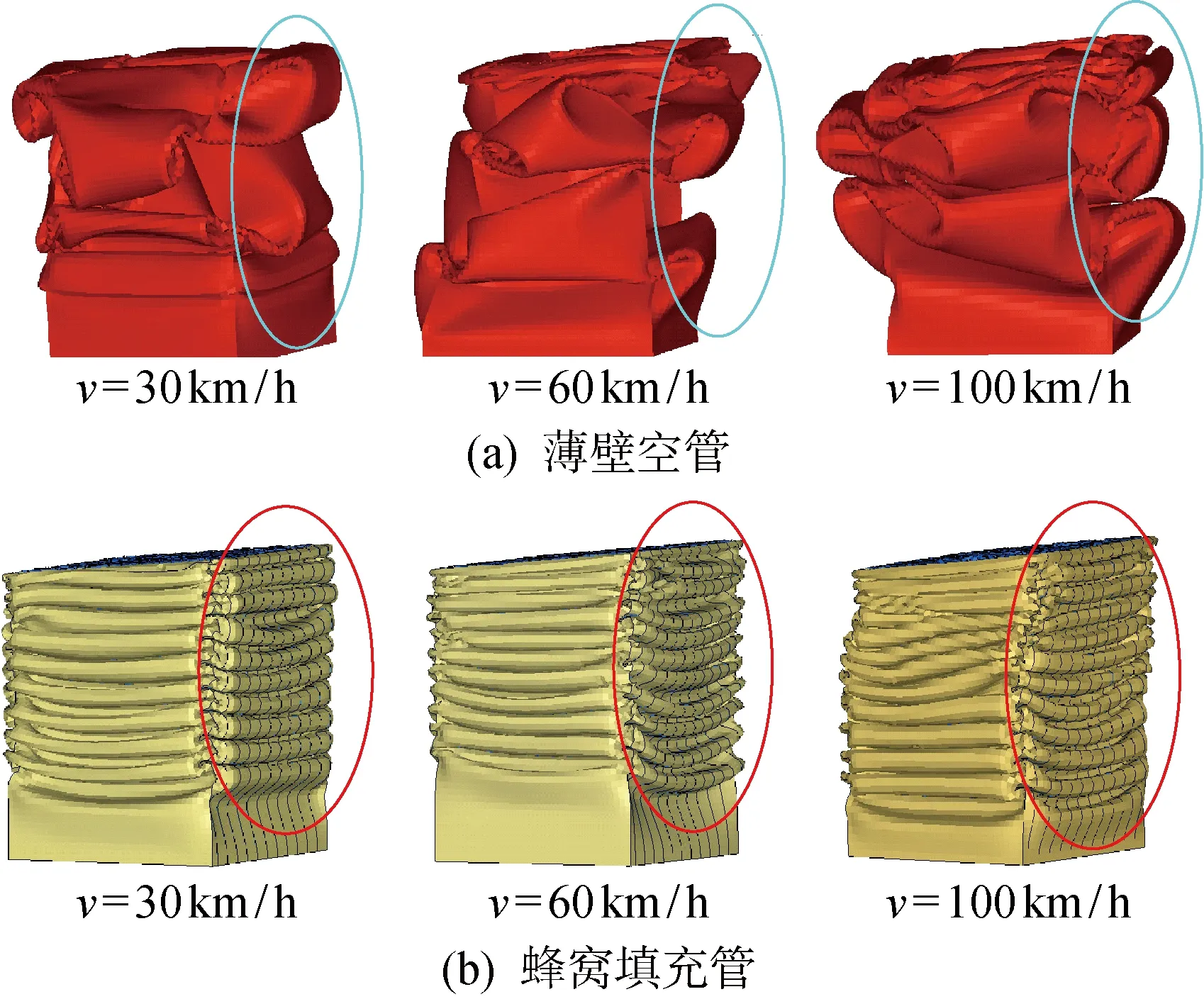
图7 不同冲击速度下蜂窝填充薄壁结构与薄壁空管的变形模式Fig.7 Deformation modes of honeycomb-filled tubes and empty tubes under different impact velocities

另外，由图5(b)还可见，当冲击角一定时，随着冲击速度增加，蜂窝填充薄壁结构和薄壁空管的SEA均有所增加，表明冲击速度引起的惯性效应对其耐撞性和吸能性均有显著影响.图7所示为α=5°，v由30 km/h增至100 km/h时薄壁空管及蜂窝填充薄壁结构的变形模式.可见，当冲击速度增加时，薄壁结构在变形与挤压的过程中拥有的惯性增强，使得相同的压缩距离内触发了更多折叠变形，从而减小了折叠波长，增加了材料利用率和吸收能量.

综合分析薄壁空管及蜂窝填充薄壁结构的比吸能(见图5)可见，与薄壁空管相比，不同的冲击工况下蜂窝填充薄壁结构的SEA都有显著提升.表2列出了不同的冲击工况下蜂窝填充薄壁结构相对于薄壁空管的SEA的提升率，即

(3)

式中：SEAf、SEAe分别为蜂窝填充薄壁结构和薄壁空管的比吸能.

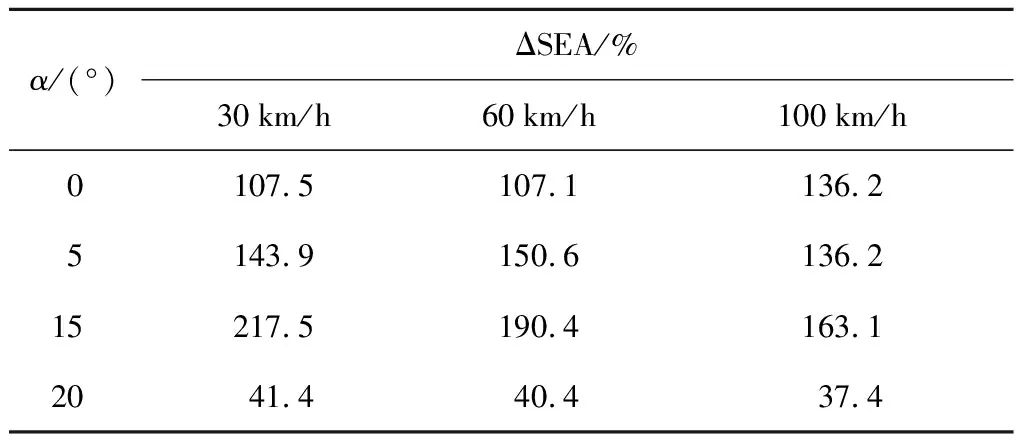
表2 蜂窝填充薄壁结构与薄壁空管的比吸能的提升率

由表2可见，在小角度(α处于0°～15°) 的冲击工况下，随着α增加，蜂窝填充薄壁结构的SEA大幅增加(1倍以上)，即使在蜂窝填充薄壁结构发生全局弯曲的大角度(α=20°)冲击下，SEA的增幅也达到约40%，表明蜂窝填充对增强薄壁结构吸能性能的作用显著，这主要是由于蜂窝芯与薄壁结构之间的交互作用[15]而使得蜂窝填充薄壁结构的变形模式更加稳定和均匀、大幅增加了其逐级折叠的次数的缘故(如见图7所示).图8示出了不同冲击工况下薄壁空管和蜂窝填充薄壁结构的冲击力峰值.由图8(a)可见，当冲击速度相同时，随着α增加，蜂窝填充薄壁结构和薄壁空管的Fmax都逐渐减小，这是由于随着α增大，刚性冲击块与薄壁结构的初始接触面积逐渐减小的缘故.然而，不同的α下薄壁结构的Fmax的降幅却不同.对于薄壁空管而言，在α<15° 的小角度冲击下，Fmax的下降率达50%，而当α由15° 增加到20° 时，Fmax的下降率低于10%，表明薄壁空管的Fmax对小角度冲击较为敏感；此外，对于蜂窝填充薄壁结构，在α<5° 的小角度冲击下，其Fmax的下降率较大，最大可达40%，而当5°<α<20° 时，其Fmax在相邻角度之间的下降率保持在16%～20%，与薄壁空管相比，其Fmax的波动幅度较小.

由图8(b)可见，当α一定时，蜂窝填充薄壁结构和薄壁空管的Fmax值都随着冲击速度增加而增加，这是因为速度越大，薄壁结构受到冲击时的惯性力越大，从而使得冲击力越大.与30 km/h的低速冲击相比，60 km/h的中速冲击时，薄壁空管在各种冲击角度下的Fmax的平均增幅为 7.24%；与60 km/h的中速冲击相比，在100 km/h的高速冲击下，各种冲击角度下薄壁空管的Fmax的平均增幅均达到 26.00%.同时，蜂窝填充薄壁结构也有类似变化规律，表明薄壁结构冲击力对高速冲击更为敏感.

综合图8中各工况下的Fmax可见，蜂窝填充薄壁结构在各工况下的Fmax都比相应的薄壁空管的Fmax大，但相对于SEA而言(见表2)，蜂窝填充薄壁结构的Fmax的提升幅度比SEA的提升幅度小.图9示出了不同的冲击工况下蜂窝填充薄壁结构和薄壁空管的SEA与Fmax的提升率.其中，Fmax的提升率可表示为

ΔFmax=(Ff,max-Fe,max)/Fe,max

(4)

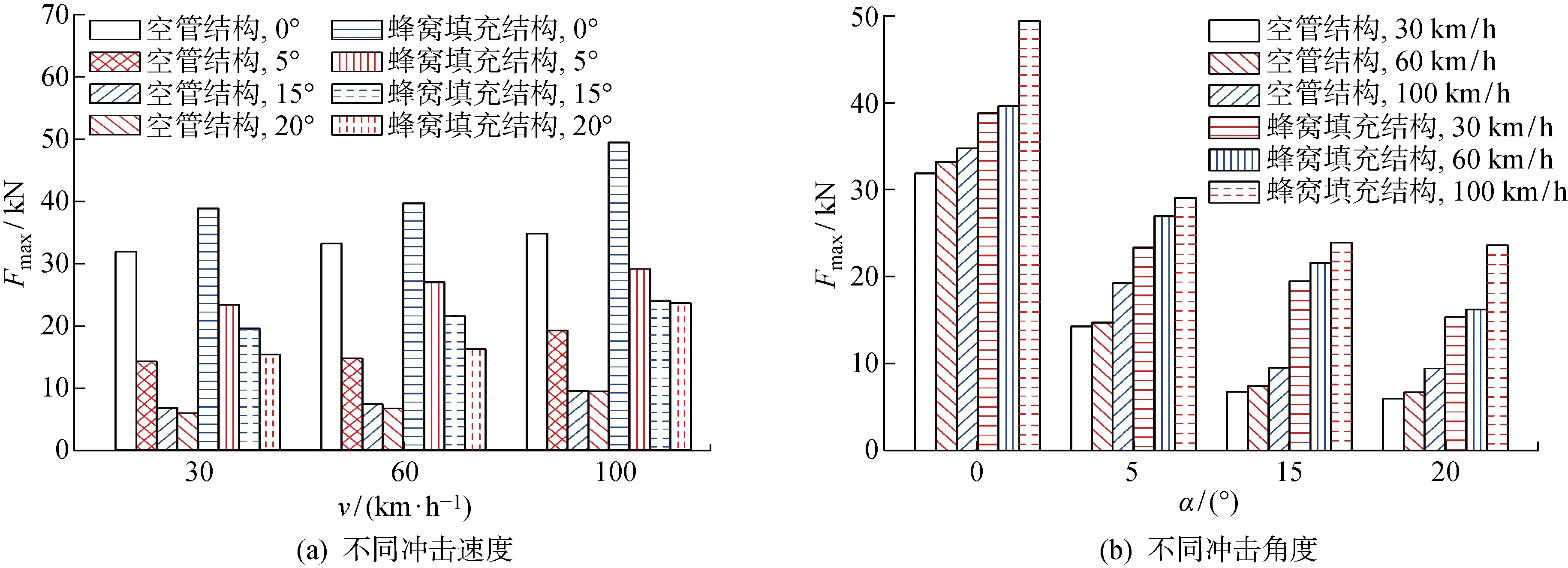
图8 多种冲击工况下蜂窝填充薄壁结构和薄壁空管的冲击力峰值Fig.8 Fmax of honeycomb-filled tubes and thin-walled hollow tubes under multiple impact loadings

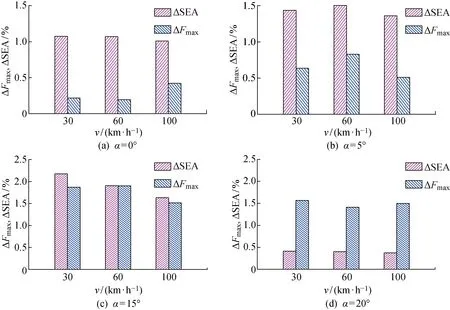
图9 蜂窝填充薄壁结构的SEA和Fmax的提升率Fig.9 Increasing rates SEA and Fmax for honeycomb-filled tube

式中：Ff,max和Fe,max分别为蜂窝填充薄壁结构和薄壁空管的冲击力峰值.

由图9可见：当α<20° 时，在所有冲击工况下ΔFmax都小于ΔSEA，且ΔFmax与ΔSEA的差距较大，其最大差值达 87.6%，表明在α<20° 的冲击工况下，蜂窝填充薄壁结构能够更好地改善薄壁空管的吸能特性；在α=20° 时，则表现为ΔFmax大于ΔSEA，这主要是由于在大角度冲击工况下蜂窝填充薄壁结构发生了全局弯曲而使其吸能性能降低的缘故.整体而言，蜂窝填充薄壁结构比薄壁空管具有更优异的耐撞性能.

3 蜂窝填充结构的优化设计

3.1 蜂窝填充薄壁结构的优化模型

合理匹配蜂窝填充薄壁结构的设计参数，使其具有最优的吸能特性仍是目前结构耐撞性设计的关键.因此，本文以外管的壁厚T以及蜂窝胞元的厚度t为设计变量，SEA与Fmax为设计响应，对蜂窝填充薄壁结构进行耐撞性的优化设计.其数学模型可表示为

(5)

式中：SEA(α,v)为设计目标，表示蜂窝填充薄壁结构在不同冲击工况(不同的α和v)下的比吸能；Fmax(α,v)为不同冲击工况下的冲击力峰值.式(5)表示在满足Fmax(α,v)不大于45 kN的条件下，使SEA(α,v)取得最大值.

本文采用对非线性响应模拟具有较高精度的 Kriging 近似技术构建蜂窝填充薄壁结构的SEA(α,v)与Fmax(α,v)的近似模型[19].首先，采用均匀拉丁方[20]实验设计方法对不同冲击工况的设计空间分别进行20次采样，以此建立SEA(α,v)与Fmax (α,v)的Kriging近似模型.由于Kriging近似模型的精度决定后续优化解的可行性，所以本文进一步采用拟合度(R2)、最大相对误差(emax)和平均相对误差(eavg)来评价其拟合精度，其定义分别为

(6)

(7)

(8)

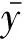
由式(6)可知，R2值越接近于1，表明Kriging近似模型越精确.

本文采用随机采样法对不同工况下的设计空间分别进行了8次采样，以验证Kriging近似模型的精度.表3列出了在α=0°，v=30 km/h的冲击工况下SEA(0,30)与Fmax(0,30)的模型精度的3个评价指标.由表3可见，R2值接近于1，emax和eavg均小于5%，而且在其他冲击工况下也可得到类似结果，表明本文所建设计响应的Kriging近似模型的精度能够满足优化设计的需求.

表3 SEA与Fmax的Kriging近似模型误差Tab.3 Error of Kriging model for SEA and Fmax

3.2 优化结果分析

采用小种群遗传算法对Kriging近似模型寻优[21]，表4列出了各工况下蜂窝填充薄壁结构的初始参数与最优参数(蜂窝最优参数取整).由表4可见，在各种工况下SEA的优化值与初始值均有所提高，但不同的冲击角下SEA提高的幅度不同.在α=0° 时，SEA的优化值比初始设计值平均提高了 3.31%；在α=5°，15° 时，SEA的优化值比初始值提高的幅度较大，分别为 22.09% 和 25.89%；在α=20°的冲击工况下，SEA的优化值比初始值平均提高了 6.84%.由此可见，优化设计可使蜂窝填充薄壁结构在斜向冲击下的SEA大幅提升，尤其是在α=15°，v=60 km/h的冲击工况下SEA的增幅达 32.76%. 图10所示为α=15°，v=60 km/h的冲击工况下初始模型和优化设计模型的冲击力与位移曲线.可见，优化使得蜂窝填充薄壁结构的冲击力有所提高，从而具有更好的吸能性能.另一方面，由表4还可以看出， 优化后的Fmax与初始设计的Fmax较为接近，表明本文提出的数值优化方法能够较好地改善蜂窝填充薄壁结构的耐撞性能，且具有较好的可行性.

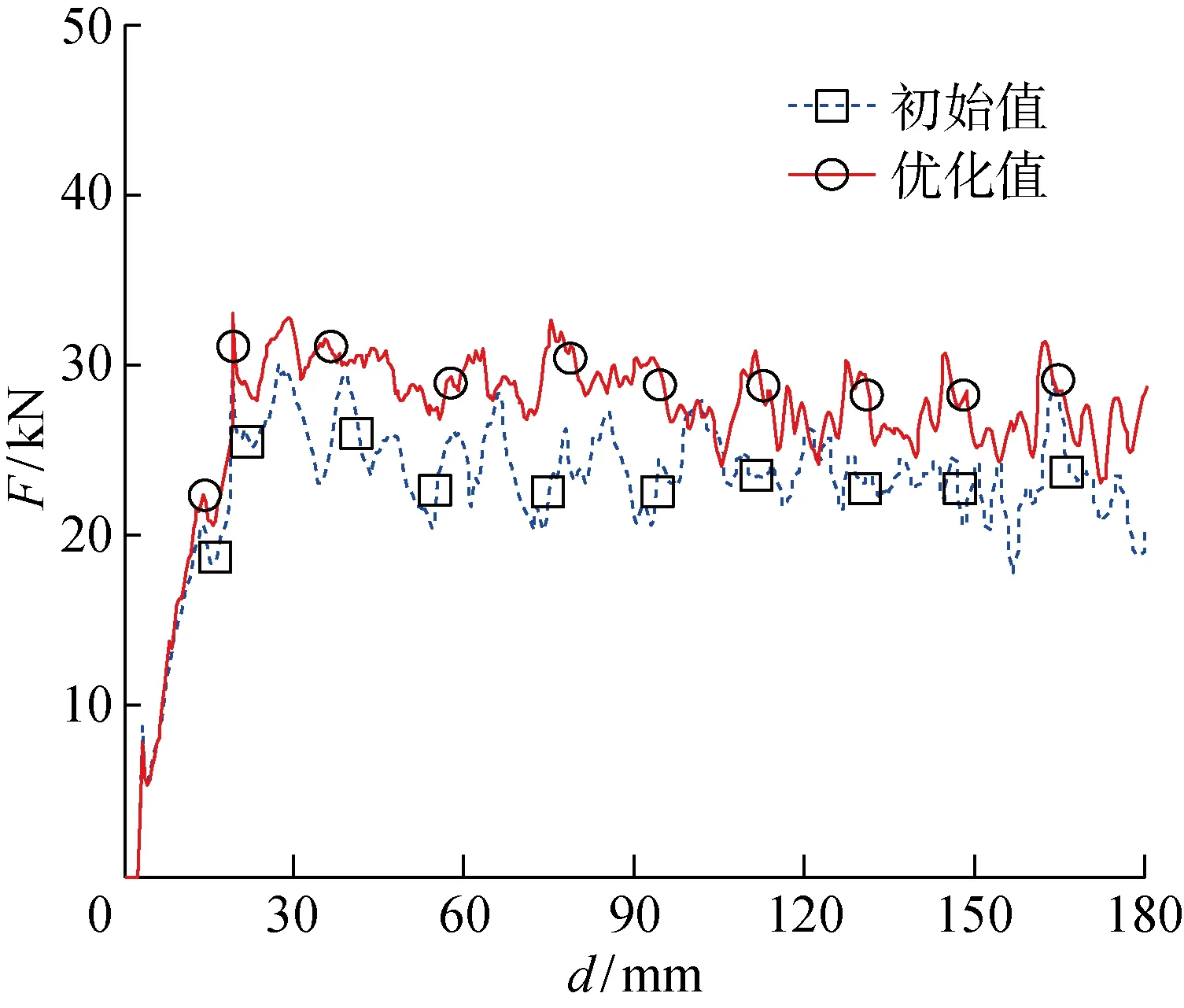
图10 初始模型和优化模型的冲击力-位移曲线Fig.10 The force-displacement curve of initial model and optimization

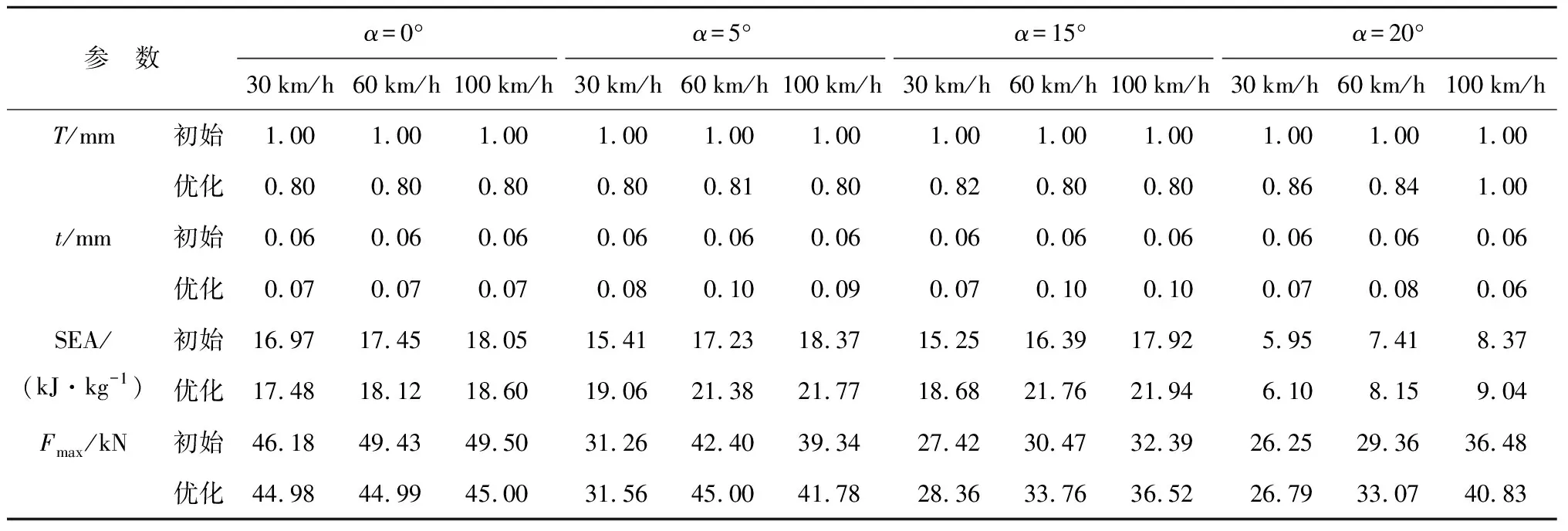
表4 蜂窝填充薄壁结构的单目标优化结果Tab.4 The optimization results of single objective for the honeycomb-filled tubes

4 结论

(1) 在不同的冲击工况下，蜂窝填充薄壁结构能够较好地改善薄壁空管变形的均匀性和稳定性.蜂窝填充薄壁结构比薄壁空管的能量吸收能力更强.

(2) 冲击速度和冲击角度对薄壁结构的耐撞性能都具有很大影响：当冲击角度一定时，随着冲击速度增加，2种薄壁结构的SEA和Fmax均逐渐增大；当冲击速度一定时，随着冲击角度增大，2种薄壁结构的SEA和Fmax均逐渐减小.

(3) 在大角度冲击下，蜂窝填充薄壁结构的第1个塑性铰发生在冲击底部，且易发生全局弯曲变形.