矩形加肋板肋条布置的无网格优化
2019-02-19,
,
(1.大连理工大学 运载工程与力学学部 辽宁 大连 116024; 2.广西大学 土木建筑工程学院 广西 南宁 530004;3. 广西大学 工程防灾与结构安全教育部重点实验室 广西 南宁 530004)
0 引言
加肋板由于具有轻质高强的优点而被广泛应用在桥梁、海洋、船舶、高铁和航空航天等领域中.在最初的研究中,主要利用梁格模型和正交各向异性板模型来模拟加肋板,而后发现这些模型仅适用于肋条布置较密的加肋板.之后的研究更倾向于将加肋板考虑为一个混合结构,肋条被看作是梁[1].在对加肋板的弯曲分析中,文献[2]利用能量的标准对加肋板在受均布荷载作用下的稳定性进行了分析;文献[3]对有纵向肋和横向肋的情况下加肋板受几种不同的弯曲荷载进行了研究;文献[4]利用一阶剪切变形理论和移动最小二乘近似求解了矩形加肋板的线性弯曲问题.无网格法因利用一系列节点而非网格离散结构,相较有限元法更多了一些灵活性.在对加肋板进行计算时,肋条上的节点分布并不需要与板上的节点对齐,肋条位置变化也不需要对板节点重新分布.文献[5]通过迭代优化算法得到了实心变厚度薄板优化问题的最优解是一个具有无限细、无限密的加肋结构.本文基于无网格法,采用移动最小二乘近似和一阶剪切变形理论得到加肋板的位移场函数,构造加肋板应变能,获得计算板挠度的控制方程,再利用约束随机方向法对加肋板的肋条位置进行优化,使加肋板中心点的挠度最小.最后用算例验证了本文方法的有效性,并对不同荷载作用下的加肋板肋条布置进行了优化分析.
1 加肋板的无网格模型
加肋板的无网格模型如图1所示.可以看出,x向肋条上的节点和y向肋条上的节点布置并没有沿着板上节点的位置布置,而是分布在板上两行或者两列节点之间.根据移动最小二乘近似[6-7],可得形函数的表达式为

图1 加肋板的无网格模型Fig.1 The meshfree model of stiffened plate
(1)
式中:P(x)代表基函数矩阵;A(x)、B(x)分别是由权函数和基函数组成的矩阵.由移动最小二乘近似和一阶剪切变形理论可以得到加肋板的位移场函数为
(2)
式中:u0pI、φpxI、v0pI、φpyI、wpI是板的节点参数;n代表板节点的个数.
x向肋条的位移场函数可以表示为
(3)
式中:u0sI、φsxI、wsxI是x向肋条上的节点参数;N是肋条上的节点总数;φxI是肋条上节点由移动最小二乘近似计算出来的形函数.
同样地,y向肋条也有相似的表达式.
1.1 位移协调条件
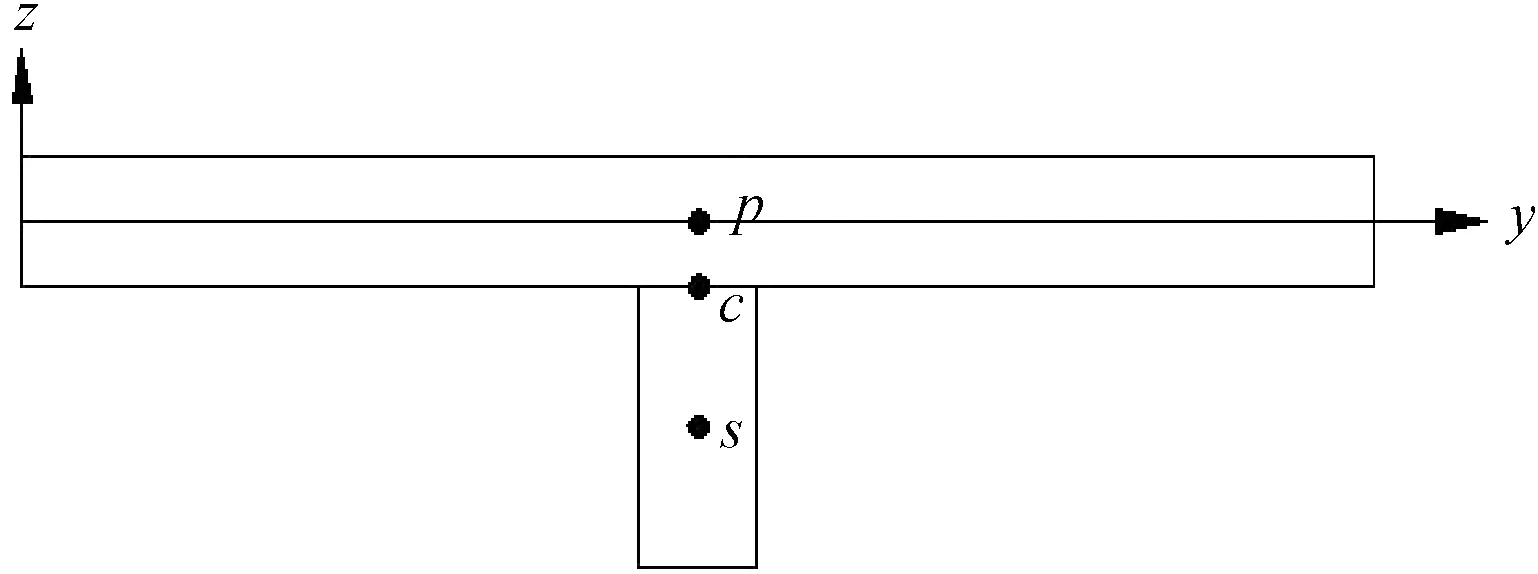
图2 加肋板的位移协调条件Fig.2 The displacement compatibility of stiffened plate
加肋板的位移协调条件如图2所示.虽然加肋板在计算时将肋条考虑为梁,但是加肋板的肋条和板是结合在一起的一个整体,所以在肋条上的某一个节点必有与之相对应的板上的点,使得它们的位移有如下关系:
[wp]p=[wsx]s,
(4)
[φpx]p=[φsx]s,
(5)
[up]c=[usx]c,
(6)
式中:p点是与肋条上节点s相对应的板上的点;c点是肋条上节点s与板上的点p之间的连线与接触面的交点.
将式(2)、 (3)带入式(4)~(6)中,可得到用矩阵形式表示的位移协调关系为
Tpδpw=Tsxδsxw,
(7)
Tpδpφ=Tsxδsxφ,
(8)
Tpδpu+esTpδpxφ=Tsxδsu.
(9)
δsx=Tspxδp,
(10)
其中:δsx=[u0s1,wsx1,φsx1,…,u0sN,wsxN,φsxN]T,δp=[u0p1,v0p1,wp1,φpx1,φpy1,…,u0pn,v0pn,wpn,φpxn,φpyn]是一个3N×3n的矩阵,当加肋板上肋条位置改变时只需要重新计算T即可.
1.2 控制方程
根据一阶剪切变形理论,加肋板的势能可以表示为
.
(11)
x向肋条的势能可以表示为
.
(12)
则加肋板的总势能可以表示为U=Up+Usx+Usy,根据虚功原理可得加肋板的控制方程为Kδp=f.
1.3 完全转换法
由于形函数并不满足N1J=δ1J的条件,所以并不能直接施加边界条件,而是需要通过一些方法使得刚度方程中的位移表现出的是真实的位移,以便施加边界条件.通过完全转换法[8]之后的节点形函数满足N1J=δ1J的条件,可以像有限元法那样直接施加边界条件.
2 约束随机方向法在肋条布置优化中的程序流程
约束随机方向法是在满足约束条件的可行范围内随机产生方向进行搜索的一种方法.这种方法主要依靠的是随机生成的点与向量,并利用随机生成的点与向量找到近似于目标函数的最速变化方向进行求导操作.因为肋条位置优化的数学模型是选取刚度方程作为目标函数,而对刚度方程进行求导是非常耗费时间的一项操作,所以选取约束随机方向法进行近似.
利用无网格法和约束随机方向法对加肋板进行优化计算,具体的程序流程如图3所示.
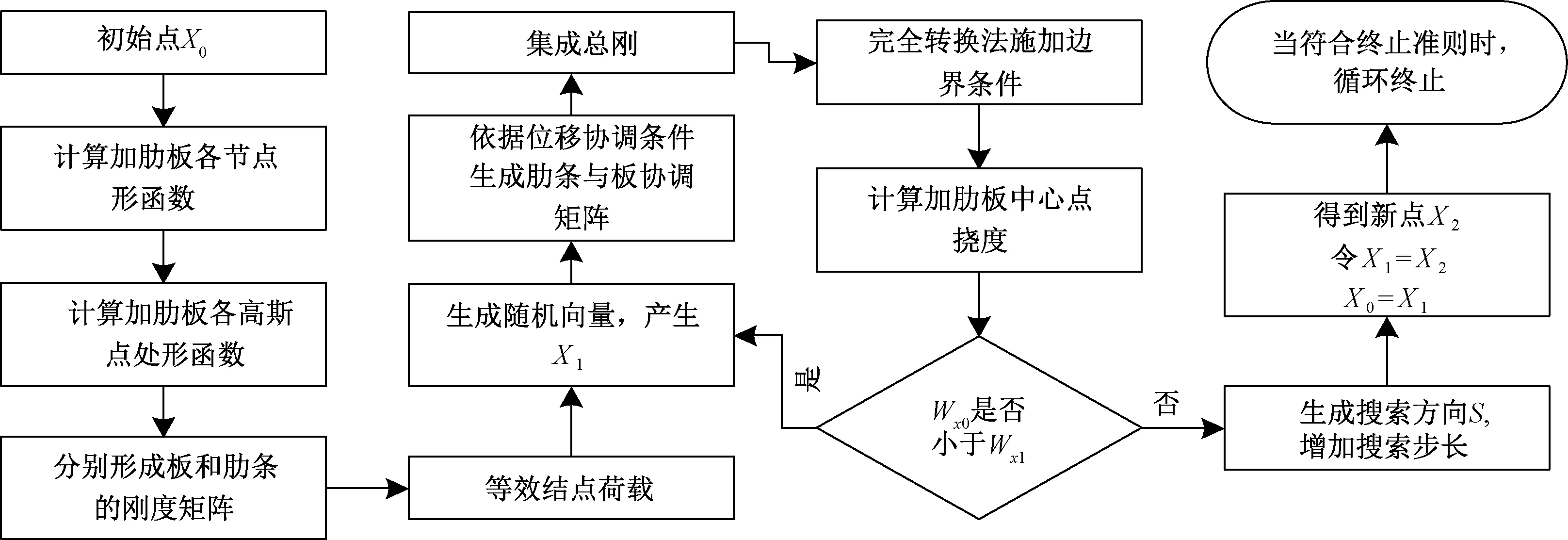
图3 基于无网格法和约束随机方向法的程序流程Fig.3 Program flow based on meshfree method and constrained random direction method
3 算例分析
3.1 验证分析

图4 单根肋条加肋板受均布荷载作用(单位:m)Fig.4 Single rib stiffened plate under uniform loads (unit: m)
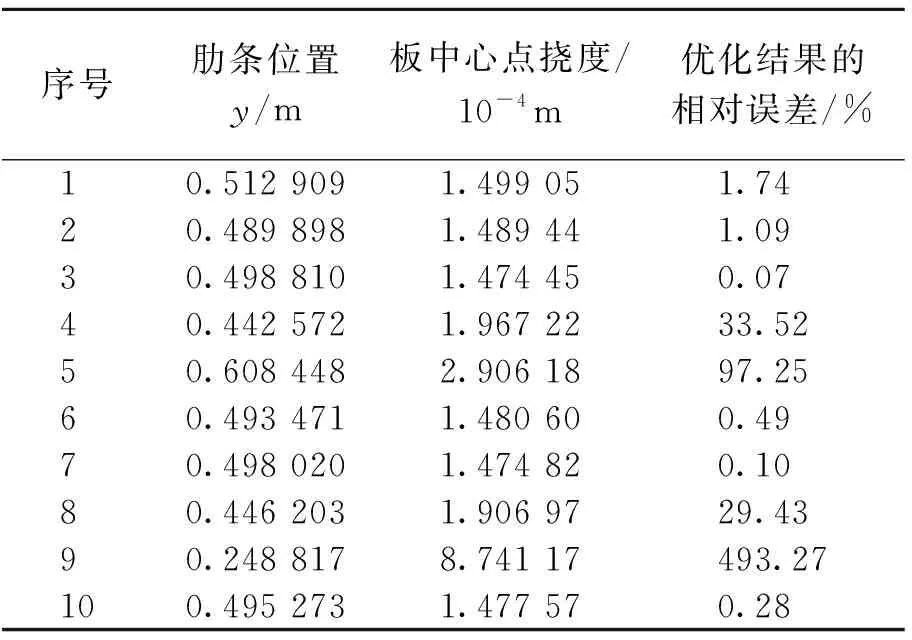
序号肋条位置y/m板中心点挠度/10-4m优化结果的相对误差/%10.512 9091.499 051.7420.489 8981.489 441.0930.498 8101.474 450.0740.442 5721.967 2233.5250.608 4482.906 1897.2560.493 4711.480 600.4970.498 0201.474 820.1080.446 2031.906 9729.4390.248 8178.741 17493.27100.495 2731.477 570.28
对约束随机方向法进行了验证分析.当加肋板受到均布荷载时,单根肋条在板中间时加肋板的挠度最小.取边长L=1 m,板厚h=0.01 m的正方形加肋板,肋条高度hs=0.1 m,肋条宽度ws=0.01 m,弹性模量E=1.7×107Pa,泊松比为0.3,受z向均布荷载1 Pa的作用,单根肋条加肋板受均布荷载作用如图4所示.
无网格模型采用9*9的均布节点离散,四边固支边界条件.采用二次基函数,权函数的支撑域大小取4倍的相邻两节点之间的距离.当两次相邻计算结果的差值小于0.01 m时,迭代终止.当肋条位于板中间时,加肋板中心点的挠度为1.473 38×10-4m.
为了验证约束随机方向法的寻优效果,对加肋板受到均布荷载的情况进行了优化分析.表1为单根肋条受到均布荷载时中心点挠度的优化结果.
由表1可以看出,有些计算结果的相对误差很大,这是因为约束随机方向法的局部寻优能力较强,随机选取的初始点对于寻优的整个过程以及寻优的效率起到非常关键的作用.随机初始点的值对于约束随机方向法来说是很重要的,往往要进行很多次计算来确定一个适用的最优设计方案.
选取结果较优的一组数据和较差的一组数据对寻优过程进行模拟,其中第7组和第9组的数据寻优过程分别如图5、图6所示.图中虚线为y=0.5 m的标准线,当初始点的取值很接近最优点时,得出的优化结果有极大概率为近似最优解.因此,对于约束随机方向法的优化需要进行多次计算.
另外,通过图形的中心点挠度曲线可以看出总趋势是趋于下降的,这就证明了约束随机方向法的迭代过程是具有优化意义的,最终得到的点一定会比初始点的值更优秀.但是,约束随机方向法仅仅可以在局部进行寻优,全局寻优能力较弱,容易找到局部最优点.
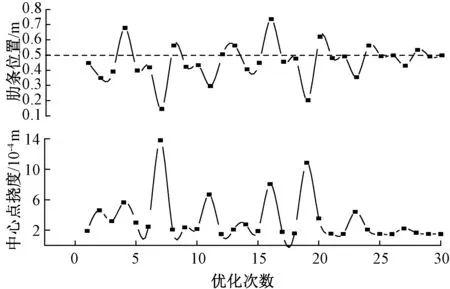
图5 第7组数据寻优过程Fig.5 The seventh set of data optimization process
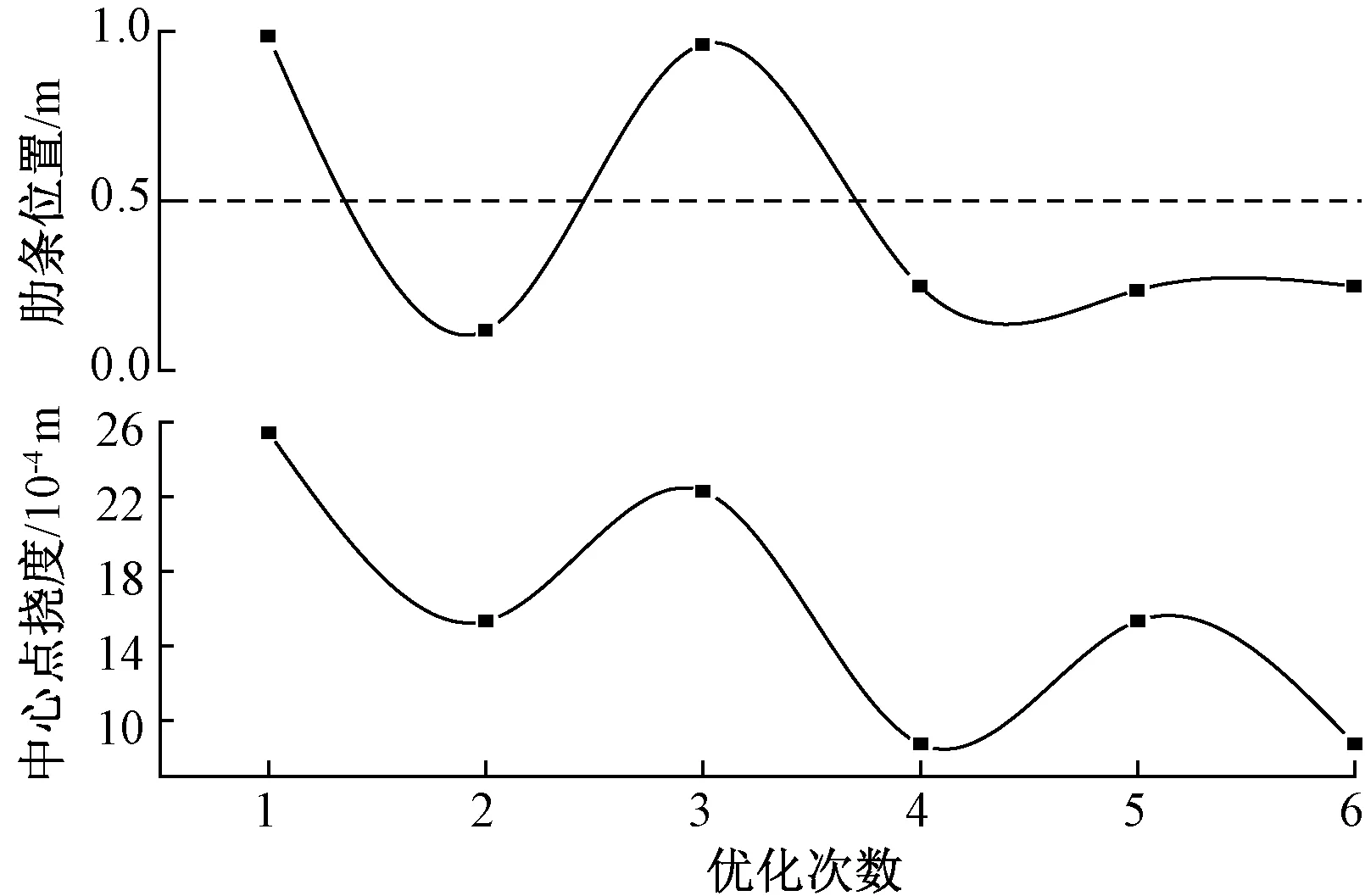
图6 第9组数据寻优过程Fig.6 The ninth set of data optimization process
图7 单根肋条加肋板受矩形局部荷载作用(单位:m)Fig.7 Single rib stiffened plate under rectangular partial loads (unit: m)

序号肋条位置y/m板中心点挠度/10-5m10.425 1391.509 9320.421 5411.524 5530.379 7652.451 3340.380 8942.408 5850.530 4805.815 5660.443 6591.609 5570.432 9791.515 9480.426 8171.506 8290.422 7311.518 52100.358 7373.417 39
3.2 加肋板肋条位置优化设计
3.2.1局部荷载下肋条的最佳位置 利用约束随机方向法对单根肋条加肋板受到局部荷载的状态进行优化设计.加肋板受到的矩形均布荷载仍为1 Pa,方向为z向,分布在左下角的正方形区域中,其他条件不变.单根肋条加肋板受矩形局部荷载作用如图7所示.
同样对受到局部荷载的加肋板进行了优化分析,分别取其中10次计算数据进行分析对比,结果如表2所示.
由表2可以看出,当肋条位置在0.43 m附近时,板中心点的挠度是最小的,最小值为1.506 82×10-5m,是由第8组数据得出的.第1组、第2组、第7组和第9组数据都很接近第8组的计算结果,也从侧面印证了第8组计算结果的准确性.由此可以得出,当单根肋条加肋板受到左下角局部荷载作用时,肋条的最佳摆放位置为0.43 m,此时加肋板中心点的挠度值为1.506 82×10-5m.
3.2.2双平行肋条加肋板位置优化 当平板中有两根肋条时,约束随机方向法的设计变量就变成了2个,且两根肋条相互平行,间距为0.3 m,受到正方形局部荷载的作用.双平行肋条加肋板受局部荷载作用如图8所示,得到的10组结果见表3.
由表3可以看出,有两根平行肋条的加肋板当固定肋条之间的距离为0.3 m,优化得到的结果是两根肋条的位置分别位于0.4 m和0.7 m时,加肋板中心点的挠度最小.
3.2.3双垂直肋条加肋板位置优化 当有两根相互垂直的肋条共同作用在板上时,同样只是对固支边界条件的加肋板进行了分析,双垂直肋条加肋板受局部荷载作用如图9所示.

图8 双平行肋条加肋板受局部荷载作用(单位:m)Fig.8 Double parallel ribs stiffened plate under partial loads (unit: m)

图9 双垂直肋条加肋板受局部荷载作用(单位:m)Fig.9 Double vertical ribs stiffened plate under partial loads (unit: m)
加肋板为1 m×1 m×0.01 m的正方形薄板,两根肋条的尺寸为1 m×0.01 m×0.1 m.受力占整个板面的四分之一,位置在加肋板的左下角.计算得到的10组结果如表4所示.
由表4可以看出,当x向肋条位于0.78 m左右、y向肋条位于0.43 m左右时,得到挠度最小的第5组数据,第9组数据也证明了在0.7 m和0.4 m附近拥有近似精确解的可能性大.所以,当双垂直肋条加肋板受到矩形局部荷载作用时,两根肋条的摆放位置在0.43 m和0.78 m处为佳.
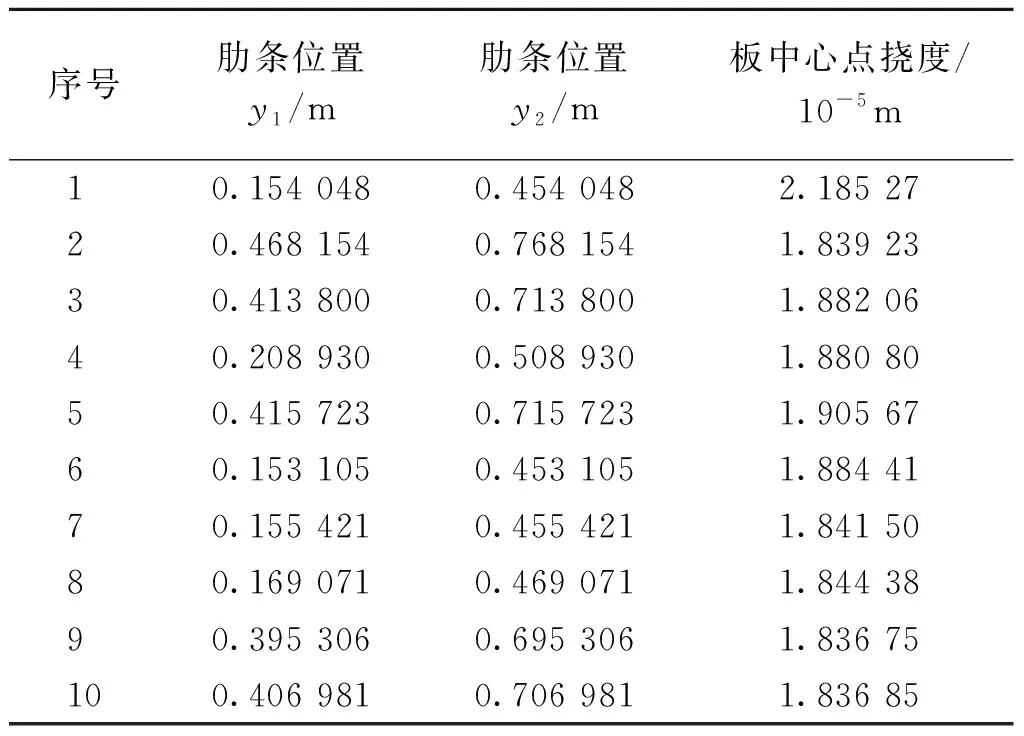
表3 双平行肋条加肋板优化结果

表4 双垂直肋条加肋板优化结果
4 结论
用约束随机方向法研究了加肋板肋条位置优化的问题.对3个算例进行计算,得出了肋条摆放位置的近似最优解.利用无网格法进行优化设计,由于约束随机方向法的局部性需要进行多次计算,但是增加的计算时间多是优化方法的计算时间;而利用有限元法进行优化计算,在重复计算的过程中增加的不仅仅是优化的时间,还有因网格重构而增加的有限元计算时间.因此,利用无网格法进行计算可以提高计算效率,效率提高程度依赖于初始点的选取.约束随机方向法计算方法简单,不需要太大的计算量,是进行小规模优化的有效计算方法.
算例中加肋板被当作板与梁的结合体,板与梁均为考虑剪切变形影响的Midlin板模型与Timoshenko梁模型.通过算例计算可以得到,在以固支边界为前提的条件下,双平行肋条加肋板在固定肋间距离为0.3 m时,两根肋条的摆放位置分别在0.4 m和0.7 m处;双垂直肋条中x向肋条的摆放位置在0.78 m、y向肋条的摆放位置在0.43 m时,加肋板中心点的挠度值最小.此方法计算简单且容易操作,但是比较容易陷入局部死点,需要通过大量的重复计算来确定优化的最终方案.
